SMA壓電復合減震裝置電力學性能及其本構模型*
展 猛, 王社良, 趙 云
(1.黃淮學院建筑工程學院 駐馬店,463000) (2.西安建筑科技大學土木工程學院 西安,710055) (3.天津大學建筑工程學院 天津,300000)
引 言
形狀記憶合金是一種應用較為廣泛的智能材料,利用其相變偽彈性設計成的SMA阻尼器已被廣泛用于土木工程結構的被動耗能減震控制中[1-2]。由于不能實時調整控制力,限制了其在結構振動控制中的應用。壓電陶瓷是一種具有瞬間電致變形特性的功能材料,其與摩擦阻尼器結合制成的壓電摩擦阻尼器是土木工程結構控制常見的一種耗能減震裝置[3-4]。但是,壓電摩擦阻尼器一般都需要施加較大的初始壓力來約束壓電驅動器的變形,其半主動可調控制力有限;而預壓力較小的話,出力也較小,大震中可能由于耗能不足而起不到有效地減震作用。將SMA材料與壓電材料制成復合型減震裝置可以實現優勢互補,對工程結構全過程起到有效減震控制,但研究處于探索階段,相關研究成果較少。王社良等[5]前期利用改進的遺傳算法,對設計的SMA壓電復合阻尼器在空間桿系結構中的優化配置進行了分析。Dai等[6]將研發的SMA壓電復合減震裝置應用于鋼框架模型的基礎隔震,進行了振動臺試驗研究。Ozbulut等[7]采用模糊控制算法對20層非線性基準結構進行了SMA壓電復合減震控制分析。
目前,SMA復合型減震裝置的本構模型大都采用“SMA數學模型+其他”的形式。例如,錢輝等[8]設計的SMA摩擦復合阻尼器,SMA單元應力采用Graesser & Cozzarelli模型,摩擦耗能單元采用Bouc-Wen模型。卞曉芳等[9]設計的SMA-磁流變(magneto-rheological,簡稱MR)復合型阻尼器,SMA單元采用Graesser模型,MR阻尼力采用Bingham模型。這些SMA復合型減震裝置的本構模型大都將SMA和其他單元割裂開,采用傳統的數學模型,不但公式繁瑣復雜、難以在Matlab程序中直接調用,而且精度很難保證。人工神經網絡是一種非線性的建模方法,該方法無需預知材料的本構形式,只需考慮影響因素和預期的目標,避免了傳統建模方法中的誤差。目前,關于SMA神經網絡本構已有一些研究。崔迪等[10]采用BP網絡分別預測了加載段和卸載段不同應變幅值的SMA的應力-應變曲線,雖然分段預測的結果精度較高,但實際應用中需將加載段和卸載段合并成完整的受力過程,此時的預測精度將難以保證。任文杰等[11]以循環次數、加卸載信息和應變值作為神經元輸入,采用徑向基函數(radial basis function,簡稱RBF)網絡預測了同一應變幅值的應力-應變曲線,該模型雖輸入參數少、便于應用,但對應變幅值在卸載的初始段無法準確預測。文獻[12]考慮加載速率和加載歷史等因素,建立了SMA的遺傳算法優化BP網絡模型,較好地預測了不同應變幅值在卸載初始段的應力-應變曲線,但該模型神經元輸入參數較多,增加了結構減震分析計算中的編程難度。神經網絡本構模型雖然有一定預測精度,但神經元初始權/閾值的變化對人工神經網絡的結果影響較大,因此建立神經網絡本構模型中應對其初始權/閾值進行優化,以提高本構模型的精度和穩定性。
筆者結合SMA材料和壓電驅動器的物理力學性能特點,提出了一種SMA單元和壓電摩擦單元依次工作的復合減震裝置,進行了相應的電力學性能試驗。在試驗結果的基礎上,以速率的符號來判斷加卸載的方向,建立了以速率符號、電壓和位移為神經元輸入的復合減震裝置BP神經網絡模型,并利用人工免疫算法對BP網絡模型的權/閾值進行了優化。
1 SMA壓電復合減震裝置
1.1 構造設計
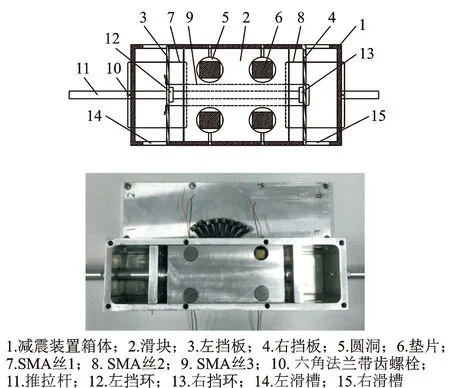
圖1 SMA-壓電復合減震裝置示意圖Fig.1 SMA-piezoelectric composite vibration damper
如圖1所示,SMA壓電復合減震裝置主要由箱體、滑塊、擋板、擋環、SMA絲和可拆卸推拉桿等組成。滑塊上有4個裝有壓電陶瓷驅動器的圓孔,上下各有一墊片,壓電驅動器的電線穿過圓洞和減震裝置箱體側壁的小圓孔與外接電源連接。SMA絲由復位絲(SMA絲1,2)和耗能絲(SMA絲3)組成,復位絲同時兼具耗能功能,每根SMA絲的兩端均由六角法蘭帶齒螺栓固定在同一側,以便減少接頭。推拉桿在兩檔中間位置斷開分成兩部分,并通過螺絲旋轉擰緊,便于安裝。擋板可以在滑槽內左右滑動,同時用來固定SMA絲3。該復合裝置的SMA和壓電摩擦單元依次工作,當發生小的振動時,SMA單獨工作;當發生大的振動時,SMA先工作,然后SMA和壓電摩擦單元同時工作,且可以實時調節控制力。
當推拉桿向左運動時,左擋環推著左擋板向左移動,SMA絲3受拉耗能;當右擋環運動至滑塊右端時,滑塊和左擋板開始一起向左運動,此時SMA絲2,3和壓電陶瓷驅動器同時耗能。當推拉桿向右運動時,右擋環頂住右擋板向右側運動,SMA絲3受拉耗能;當左擋環運動至滑塊左端時,滑塊和右擋板開始一起向右運動,此時SMA絲1,3和壓電陶瓷驅動器同時耗能。
1.2 性能試驗
1.2.1 加載方案
考慮到SMA壓電復合減震裝置試驗模型的尺寸以及 SMA 絲在減震裝置中的固定,本次試驗所用SMA絲直徑為0.7 mm,化學成分為Ti-51%atNi。相變溫度:Mf為-42℃,Ms為-38℃,As為-6℃,Af為-2℃,該絲在常溫狀態下處于奧氏體狀態。在復合減震裝置試驗之前,首先對奧氏體SMA絲進行力學試驗,以確保SMA絲的性能滿足復合裝置的耗能要求。鑒于目前單純SMA絲試驗研究較多,這里就不在贅述,僅給出復合裝置的電力學試驗。各項材料具體參數:SMA絲的最大應變幅值按7%計算,SMA絲3的數量為2根,長度為175 mm,單獨工作位移為5 mm,最大伸長量為12 mm;SMA絲1,2卸載時其力比較小且行程較短,為保證復位效果,數量取為4根,長度取為100 mm,最大伸長量為7 mm;壓電陶瓷驅動器是蘇州攀特電陶科技股份有限公司研制的型號為PTJ1501010301的矩形壓電陶瓷驅動器,各項性能指標如表1所示。
表1 矩形壓電陶瓷驅動器主要性能指標
Tab.1 Performance indicators of piezoelectric actuator

參數指標數值型號PTJ1501010301外形尺寸(A×B×H)/mm10×10×36標稱位移/μm400位移推力/N3 600剛度/ (N·μm-1)90最大預壓力/N2 000壓電應變系數d33/(10-12C·N-1)≥650
該試驗在某動靜材料試驗機上進行,試驗采用位移控制,三角波加卸載。大量研究證明,頻率對SMA絲和壓電智能阻尼器力學性能影響很小[13-14],這里激勵頻率取0.05,0.1,0.2和0.3 Hz,加載幅值分別為5 mm(SMA絲3單獨工作)、9 mm和12 mm。激勵電壓分別為0,40,80和120 V。試驗前,復合裝置在頻率為0.1 Hz,電壓為0,最大位移為12 mm 處拉壓循環30次,以保證SMA 絲的力學性能達到穩定。試驗時每個工況拉壓循環2圈。試驗裝置如圖2所示。

圖2 試驗裝置Fig.2 Test apparatus
1.2.2 試驗結果
圖3為不同頻率時SMA絲3單獨工作時的控制力-位移曲線。限于篇幅,圖4僅給出了施加40 V和80 V電壓下不同頻率的輸出力-位移曲線。可以看出,該復合減震裝置可以雙向受力,滯回曲線飽滿且基本對稱,耗能能力較好、性能穩定,加載頻率對減震裝置的性能幾乎沒有影響。
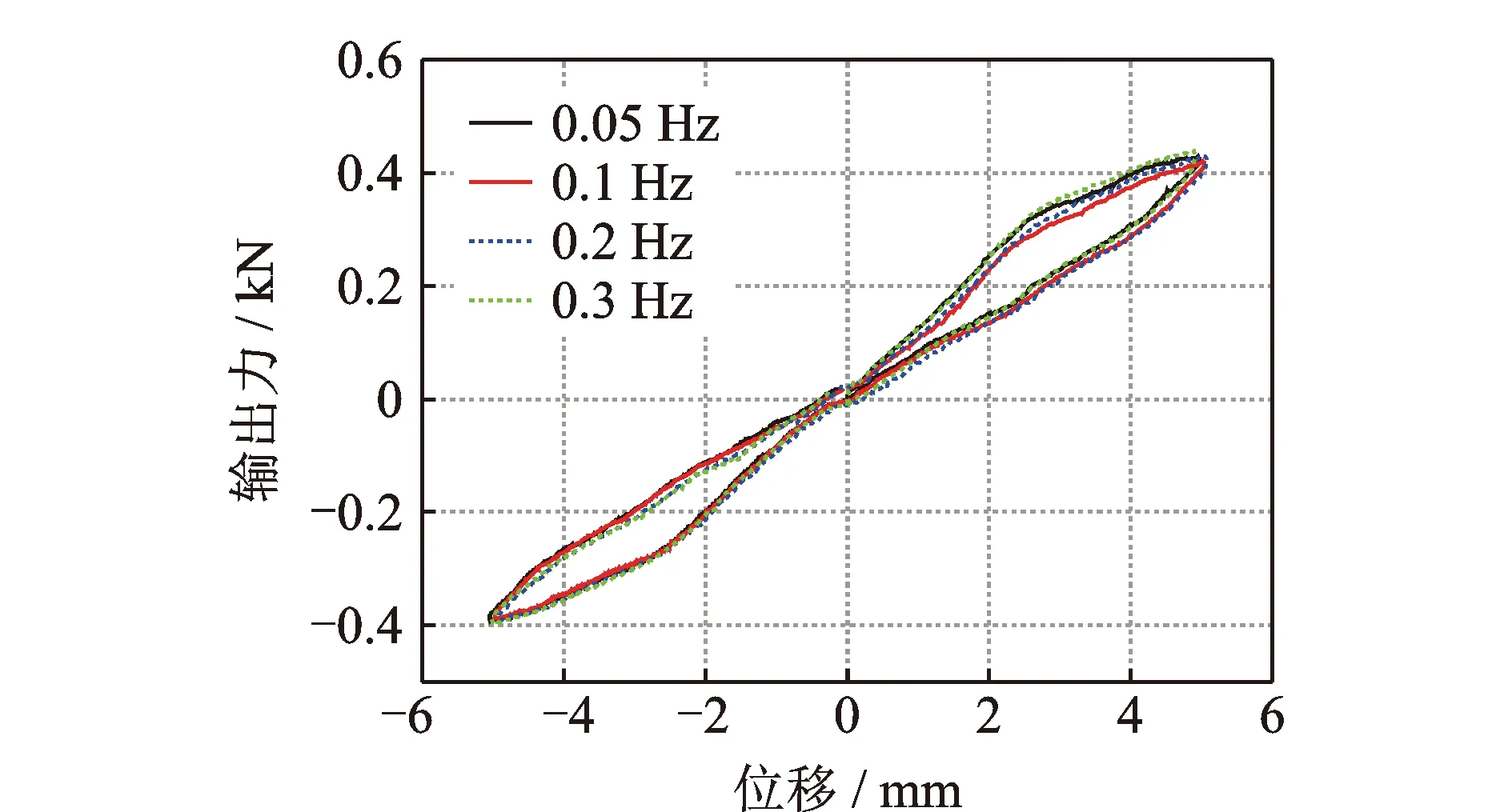
圖3 SMA絲3單獨工作時的輸出力-位移曲線Fig.3 The output force-displacement curves when SMA wire 3 alone works
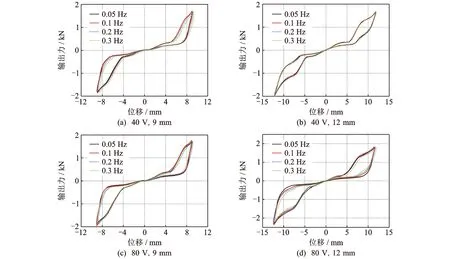
圖4 不同頻率下的輸出力-位移曲線Fig.4 The output force-displacement curves under different frequencies
鑒于頻率對試驗結果影響較小,這里僅給出0.1 Hz下不同電壓的控制力位移曲線,如圖5所示。可以看出,當位移幅值大于5 mm時,由于復位絲和初始摩擦力的介入,控制力顯著增大;且隨著電壓的增大,滯回環的面積逐漸增大,耗能能力不斷增強。由于預緊螺栓為點固定,不能使摩擦面上的摩擦力絕對均勻,因此滯回曲線并非完全對稱,這里取其絕對平均值作為最大控制力,如表2所示。圖6為不同位移幅值時各工況對應的最大輸出力曲線。可以看出,壓電陶瓷驅動器提供的控制力與輸入電壓值近似呈線性關系。
壓電陶瓷驅動器提供的控制力并不能直觀反映其對復合減震裝置耗能能力的貢獻,為了分析施加電壓下SMA壓電復合減震裝置的力學性能,現定義以下指標。
1) 單圈循環耗能Wd為一次拉壓循環滯回曲線包圍的面積,表示復合減震裝置每個循環的耗能能力。耗能提高率α為施加電壓后減震裝置耗能量的提高率,表達式為
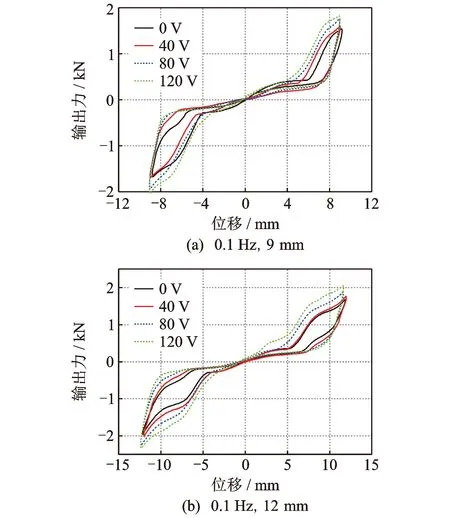
圖5 不同電壓時的輸出力-位移曲線Fig.5 The output force-displacement curves under different voltages
表2 不同電壓下的平均最大控制力
Tab.2 The average maximum control force under different voltages
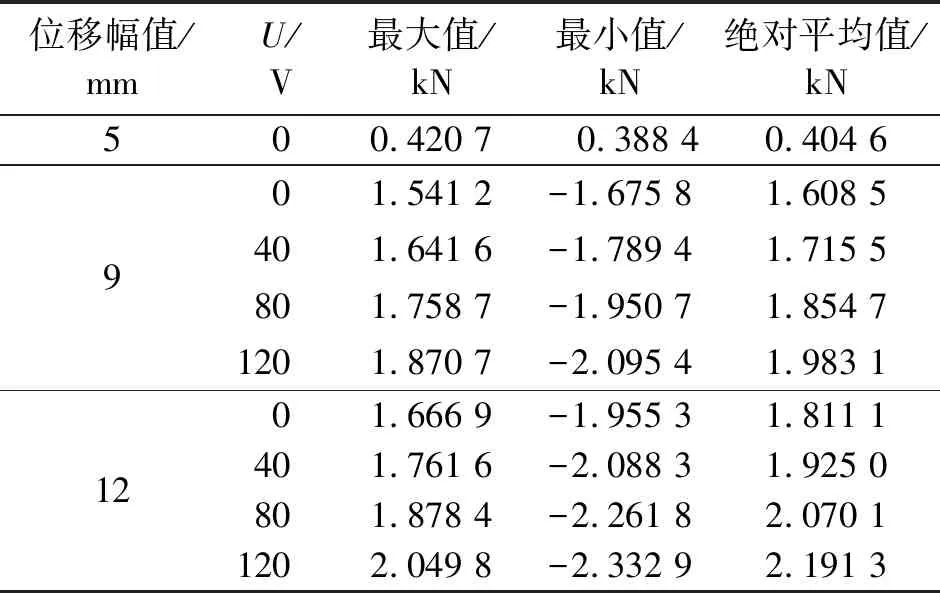
位移幅值/mmU/V最大值/kN最小值/kN絕對平均值/kN500.420 7 0.388 40.404 6901.541 2-1.675 81.608 5401.641 6-1.789 41.715 5801.758 7-1.950 71.854 71201.870 7-2.095 41.983 11201.666 9-1.955 31.811 1401.761 6-2.088 31.925 0801.878 4-2.261 82.070 11202.049 8-2.332 92.191 3
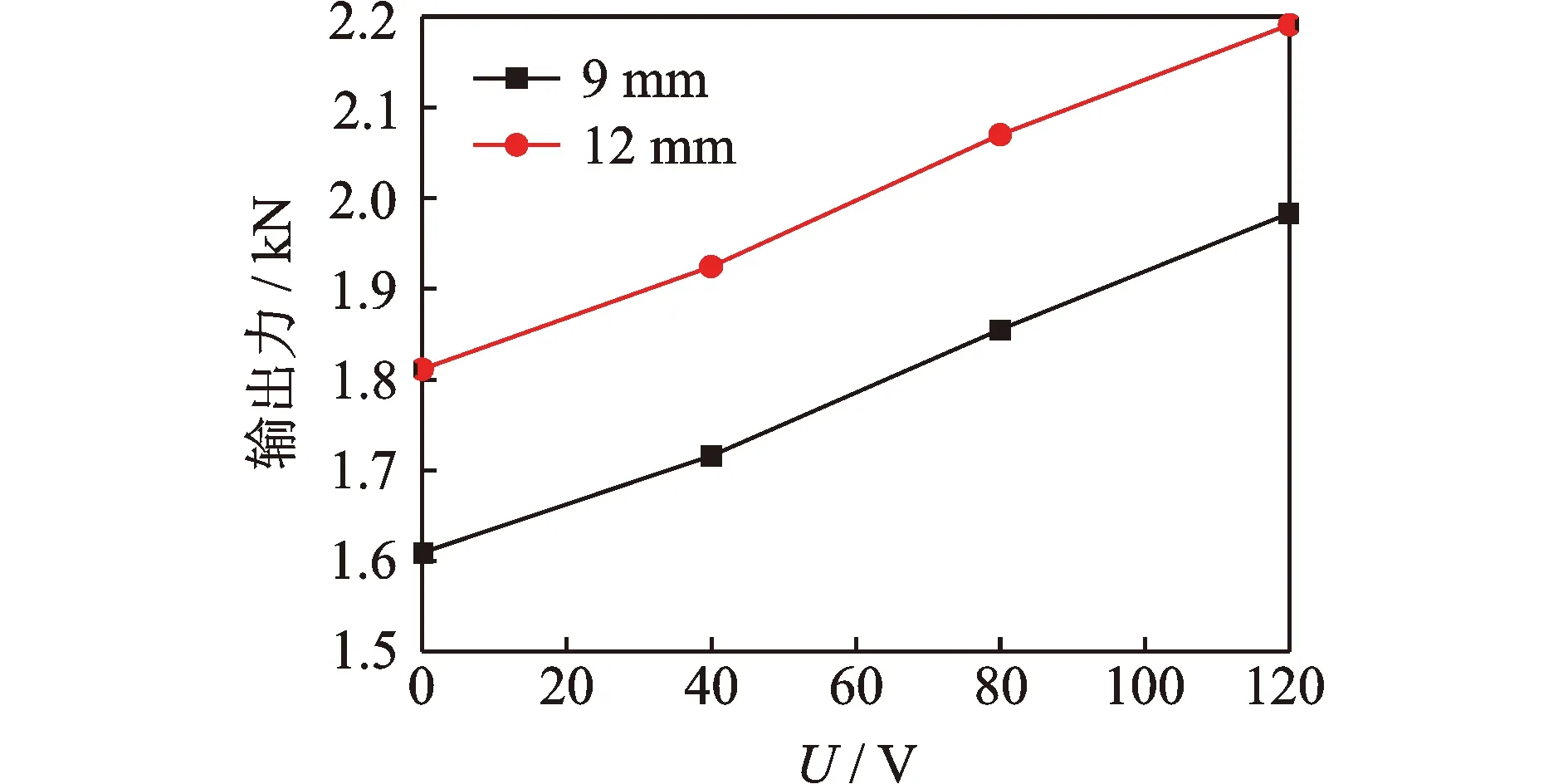
圖6 不同電壓時的最大輸出力曲線Fig.6 The maximum output force curves under different input voltages
α=(WdU-Wd0)/Wd0
(1)
其中:Wd0為0 V所對應的單圈循環耗能;WdU為除0 V外,其他電壓下的單圈循環耗能。
2) 單圈循環的等效割線剛度Ks的表達式為
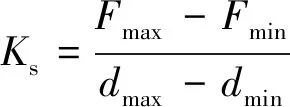
(2)
其中:Fmax,Fmin為單圈循環中的最大和最小控制力;dmax,dmin為單圈循環中的最大和最小位移。
3) 單圈循環的等效阻尼比ζa表示SMA壓電復合減震裝置的阻尼能力,表達式為
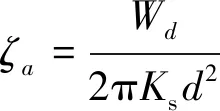
(3)
其中:d為一次拉壓循環中位移幅值。
SMA壓電復合減震裝置的各項力學性能指標如表3所示。圖7為不同電壓時的單圈耗能曲線。可以看出,同一位移幅值下,隨著電壓的增加,耗能量逐漸增大,相鄰電壓間的耗能增量不斷增大;相比位移幅值9 mm下,12 mm時的耗能量隨電壓增加的更快,且同一電壓下的耗能增量隨電壓增加不斷增大。這主要是因為隨著電壓或位移幅值的增大,滯回環的面積增大,在增加相同的控制力時,滯回環增加的面積也越大。電壓從0 V增加到120 V,位移幅值為9 mm時單圈耗能量提高了83.34%,位移幅值為12 mm時單圈耗能量提高了138.23%。壓電陶瓷驅動器提供的半主動控制力在數值上看起來雖然并不大,但對SMA壓電復合減震裝置的耗能能力卻提高較多。
表3 SMA壓電復合減震裝置的力學性能指標
Tab. 3 Mechanical performance indicators of composite vibration damper
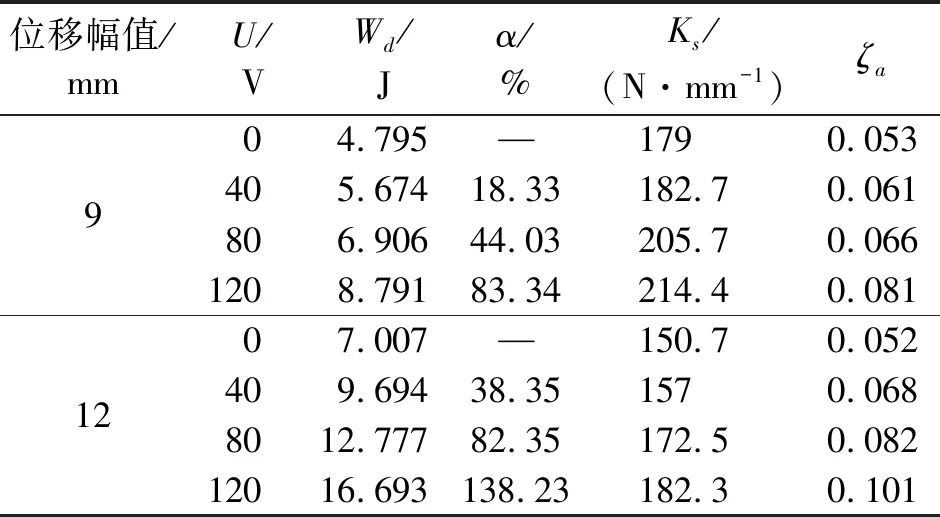
位移幅值/mmU/VWd/Jα/%Ks/(N·mm-1)ζa904.795—1790.053405.67418.33182.70.061806.90644.03205.70.0661208.79183.34214.40.0811207.007—150.70.052409.69438.351570.0688012.77782.35172.50.08212016.693138.23182.30.101
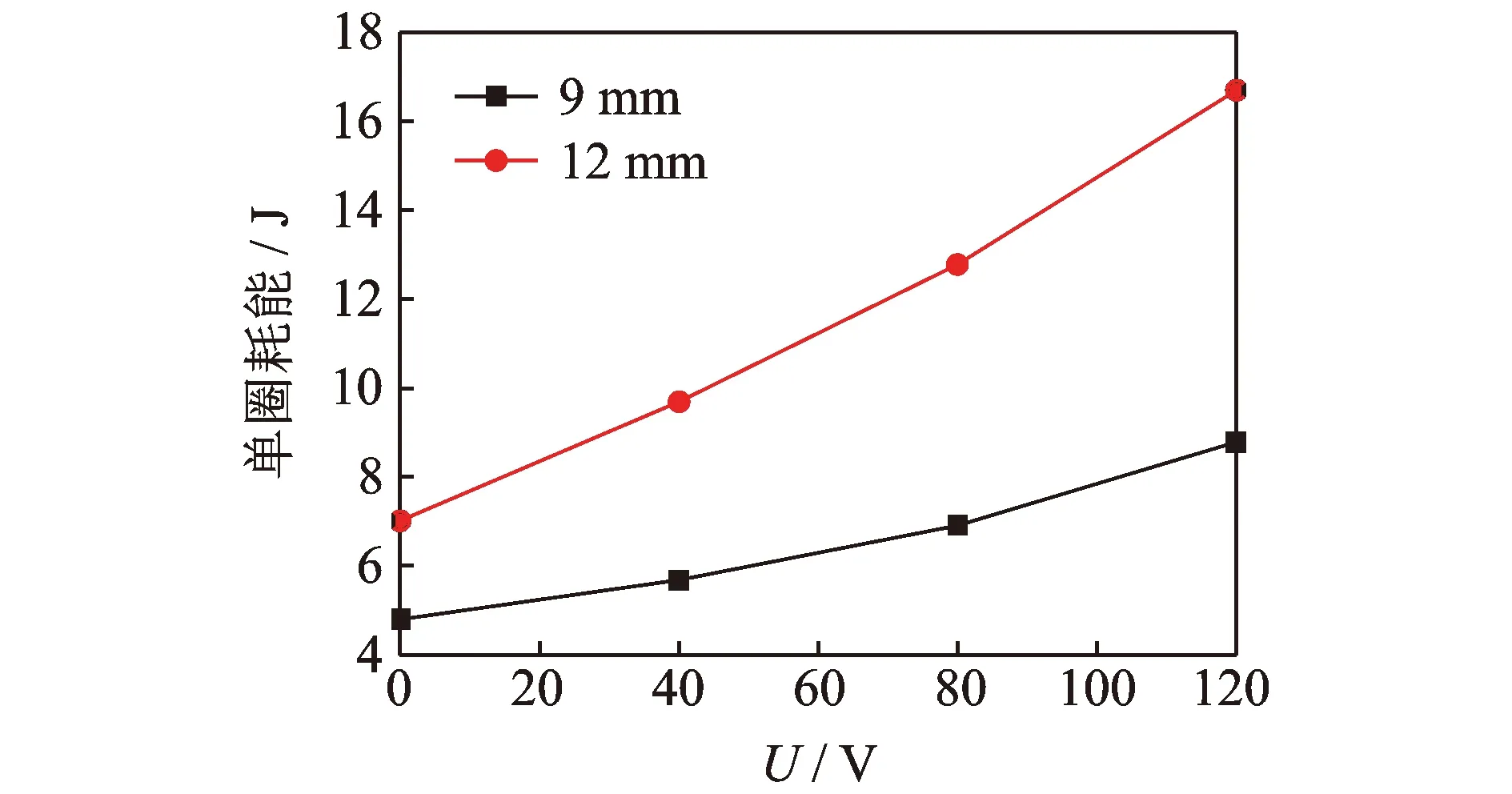
圖7 不同電壓時的單圈耗能值Fig.7 Lap value of energy consumption under different input voltages
圖8為等效割線剛度和等效阻尼比隨輸入電壓的變化曲線。同一位移幅值下,隨著電壓的增加,等效割線剛度和等效阻尼比都不斷增大。電壓從0 V增加到120 V時,位移幅值9 mm時的等效割線剛度提高了19.78%,等效阻尼比提高了52.83%;位移幅值12 mm時的等效割線剛度提高了20.97%,等效阻尼比提高了94.23%。隨著位移幅值增大,等效割線剛度減小,等效阻尼比增大,耗能能力增強。隨著電壓的增大,不同位移幅值的等效割線剛度的增量變化較小,而此時的單圈耗能增量增大(圖7),因此等效阻尼比的增量也逐漸增大。
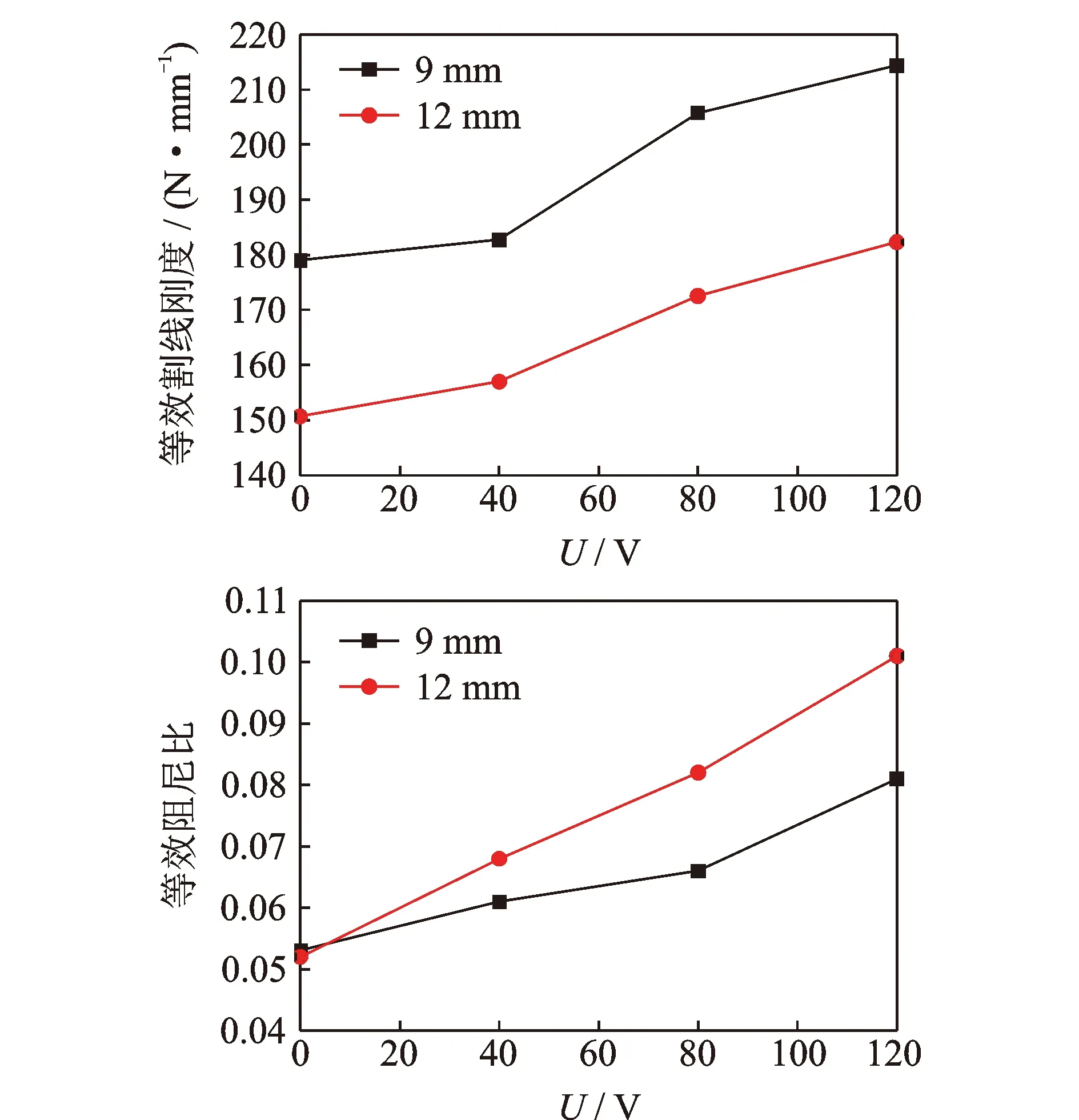
圖8 等效割線剛度和等效阻尼比隨電壓變化曲線Fig.8 Equivalent secant stiffness and damping ratio curves under different voltage
2 復合減震裝置神經網絡本構模型
2.1 網絡結構
以速率的符號來判斷加卸載的方向,同時考慮施加電壓的影響,建立3層BP神經網絡模型來預測SMA壓電復合減震裝置的輸出力。由于頻率對試驗結果影響較小,且沒有呈現明顯的規律性,因此SMA壓電復合減震裝置神經網絡本構模型不再考慮頻率因素,其神經元輸入為電壓、位移和速率符號,隱層通過估算法確定[15],取10個,神經元輸出為控制力,拓撲結構為3-10-1。
2.2 樣本數據
由于SMA壓電復合減震裝置試驗工況較少,施加電壓的位移幅值只有2個,且每個工況僅循環了2圈,可以把不同頻率的試驗數據看成圈數,以增加樣本數量,同時不再預測不同位移幅值的輸出力-位移曲線,僅考慮不同電壓下的本構曲線預測。試驗工況共有8個,選取其中2組作為檢驗數據,分別為:a.位移幅值為9 mm、電壓為80 V;b.位移幅值為12 mm、電壓為80 V。其余6種工況為訓練樣本。
2.3 優化參數
未經優化BP網絡的初始權/閾值由系統隨機分配;而經優化BP網絡的初始權/閾值由人工免疫算法[16]尋優確定。由BP網路的結構可知,BP網絡待確定的權值有3×10+10×1=40個,待確定的閾值有10+1=11個,因此優化算法的變量為所有權值和閾值,變量總數為51個。采用實值編碼,染色體長度為51,目標函數取訓練樣本經BP網絡預測所得的期望輸出與實際輸出的誤差平方和。人工免疫算法的其他參數設置如下:初始抗體種群為10,克隆規模為10,變異概率為0.005,一般抗體單元概率閾值取0.1,記憶單元概率閾值取0.01,記憶單元個體數量為5。
2.4 仿真結果
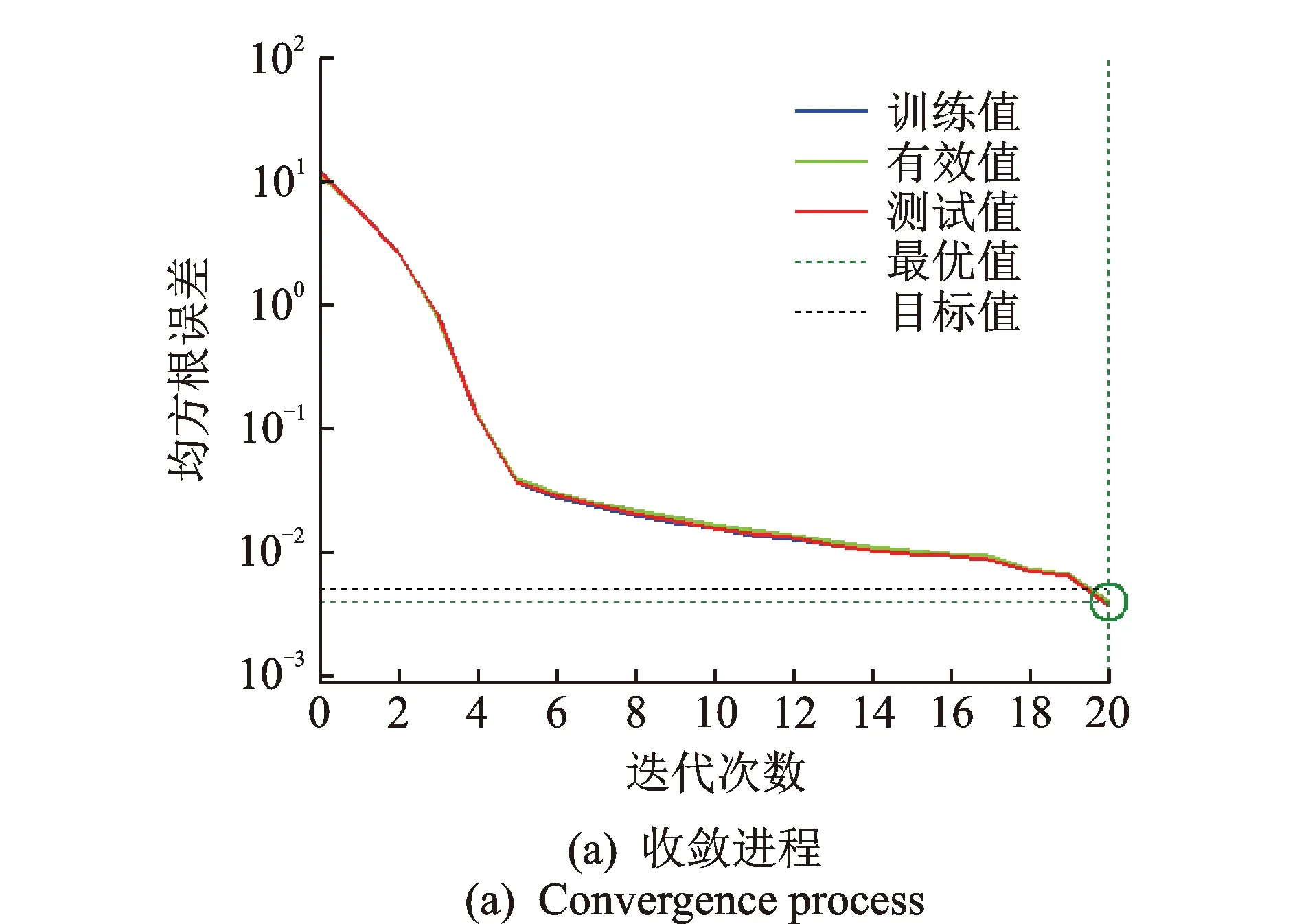
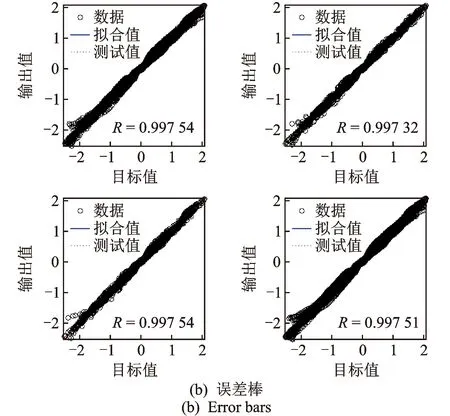
圖9 第2組檢驗數據的收斂進程Fig.9 Convergence process of the second group test data
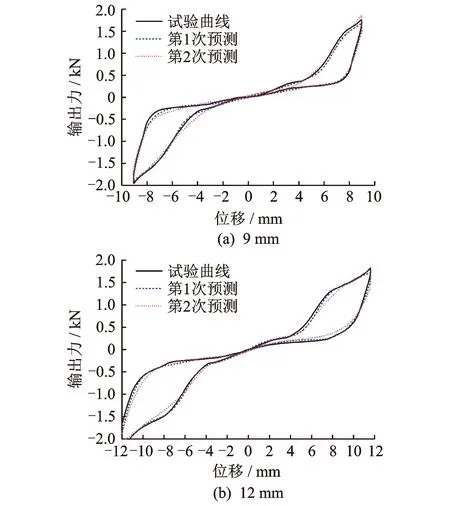
圖10 未優化預測曲線與試驗曲線對比Fig.10 The comparison between no optimization forecasting curve and test curve
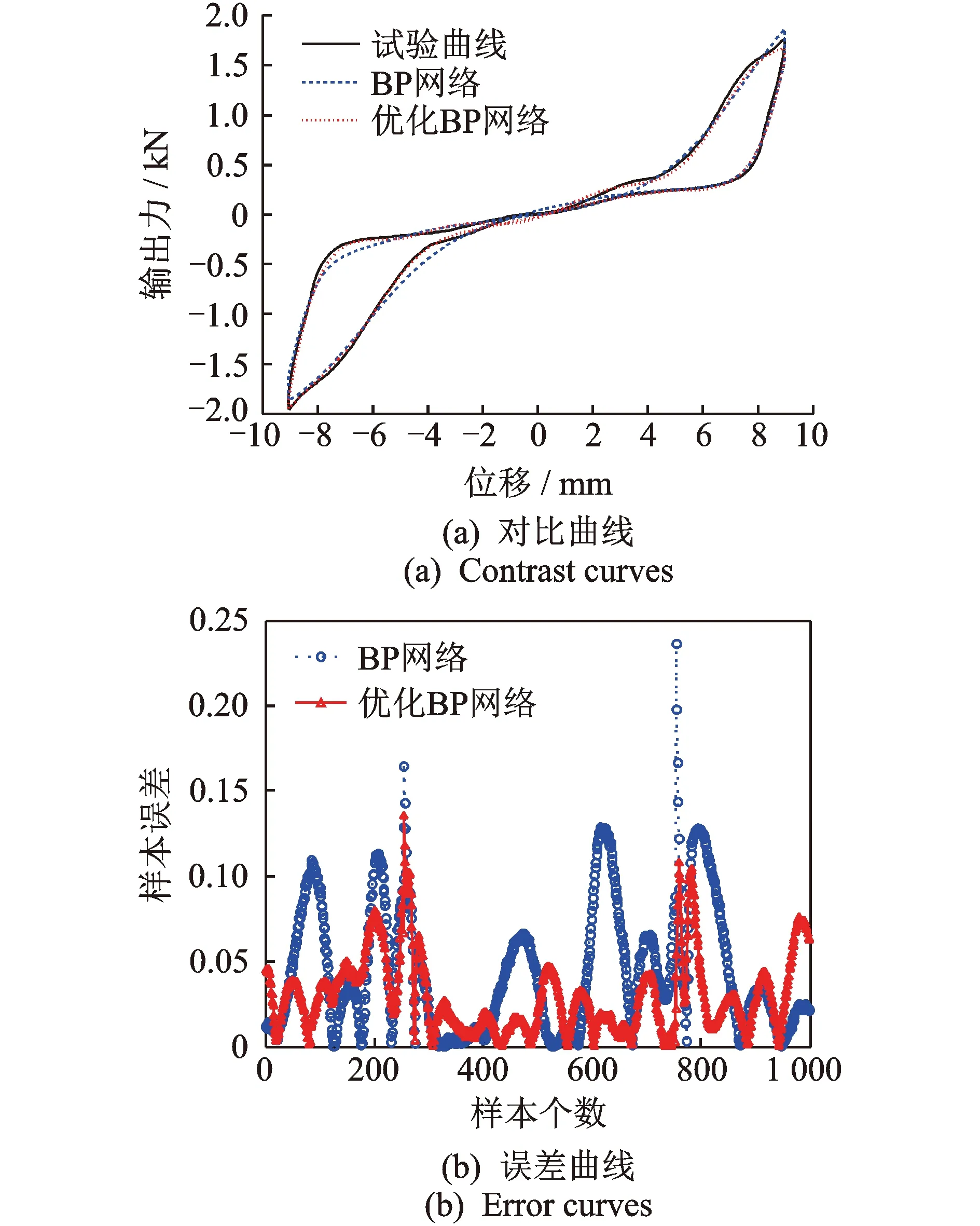
圖11 位移幅值9 mm時的預測曲線與樣本絕對誤差Fig.11 Prediction curve and absolute error at 9 mm
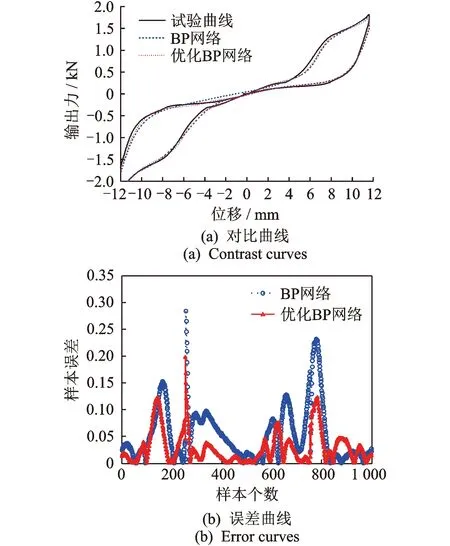
圖12 位移幅值12 mm時的預測曲線與樣本絕對誤差Fig.12 Prediction curve and absolute error at 12 mm
圖9為第2組檢驗數組神經網絡預測模型的收斂進程。由于神經網絡每次運行得到的結果都在變化,而理論上未優化的BP網絡在多次運行中也能找到最優值,因此這里采取隨機運行進行優化與未優化對比。圖10為隨機二次運行的未優化BP預測曲線與試驗曲線的對比圖。可以看出,由于初始權/閾值的隨機性,使每次訓練學習后得到的BP網絡波動較大。圖11,12為試驗曲線與未優化BP網絡、優化BP網絡預測曲線的對比圖與樣本絕對誤差圖。可以看出,除個別點偏差較大外,大部分數據點誤差控制在0.2 kN以內,能夠滿足實際應用需要。優化與未優化BP網絡模型均能較好地預測復合減震裝置在施加電壓下的輸出力,但優化后BP網絡更穩定、精度更高,可以快速得到誤差更小的網絡模型。
3 結 論
1) 該復合減震裝置滯回曲線飽滿且基本對稱,耗能能力較好,性能穩定。隨著電壓的增大,滯回環的面積逐漸增大,耗能能力不斷增強。在位移幅值為12 mm、電壓為120 V下,單圈耗能量提高了138.23%,等效阻尼比提高了94.23%。可見,SMA壓電復合減震裝置具有較好的半主動耗能能力。
2) 由于神經網絡的初始權/閾值為人工免疫算法尋優得到的最優初始權/閾值,相比未優化的BP網絡而言,優化后的BP網絡提高了預測模型的穩定性,可以更加快速地得到誤差更小的網絡模型。
3) 除個別點偏差較大外,BP網絡模型預測后的大部分數據點誤差控制在0.2 kN以內,可以滿足實際應用需要,且這種以速率符號、電壓和位移為神經元輸入的BP神經網絡本構模型便于在Matlab中實現,為SMA復合類減震裝置本構模型的建立和應用提供了新途徑。

