SLCE 序列的2-adic 復雜度

王艷，李順波，薛改娜

（西安建筑科技大學理學院，陜西 西安 710055）

1 引言

周期偽隨機序列在通信和密碼領域有著廣泛的應用。有關周期序列的自相關性、線性復雜度及2-adic 復雜的研究一直是序列研究的熱點。

周期序列可以由線性移位寄存器(LFSR，linear feedback shift register)生成，也可以由帶進位的移位寄存器(FCSR，feedback with carry shift register)生成。生成序列的最短LFSR 的級數稱為該序列的線性復雜度，生成序列的最短FCSR 的級數稱為該序列的2-adic 復雜度。由B-M (Berlekamp-Massey)算法和有理逼近算法可知，獲得連續2 倍線性復雜度或2 倍2-adic 復雜度長的序列，便可以恢復生成該序列的LFSR 或FCSR，因此，周期序列的設計要求高線性復雜度、高2-adic 復雜度。同時，序列的自相關性也是衡量序列的一個重要指標，好的序列應該有低的自相關值。

SLCE (Sidelnikov-Lempel-Cohn-Eastman)序列是一類偶周期分圓序列，由Sidelnikov[1]首次提出，故有文獻稱該類序列為Sidelnikov 序列；Lempel、Cohn 和Eastman[2]研究了該類序列的自相關性，使該序列受到關注，因而很多文獻中以這4 人的姓名首字母的縮寫（SLCE）命名這種分圓序列。SLCE序列的線性復雜度一度是一個難題，Kyureghyan 等[3]發現SLCE 序列的線性復雜度與一類分圓數的余數及 Jacobsthal 和有關，推進了此項研究工作。Helleseth 等[4-5]給出了p=3,5,7 時，周期為pm-1 序列的線性復雜度；Meidl 等[6]利用分圓數確定了某些具體序列的線性復雜度。之后關于SLCE 序列1-錯線性復雜度[7]、線性復雜度的界[8-9]、特征值[10]等研究陸續出現。基于這些研究，SLCE 序列的2-adic 復雜度也成了一個有意義的問題，本文主要研究SLCE 序列的2-adic 復雜度。

2 基礎知識

2.1 SLCE 序列

設q為奇素數p的冪，即q=pm，記Fq為q元有限域，α為Fq的本原元，即Fq的乘法群的生成元。定義中的二次特征為

設q=df+ 1，〈αd〉為由αd生成的乘法子群，稱陪集為關于Fq的d階分圓陪集。顯然此處依賴于α的選擇，于是有

引理1[11]若q≡ 1(mod4)，則有

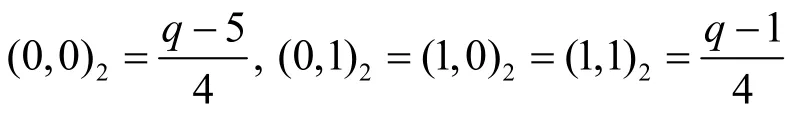
若q≡ 3(mod 4)，則有

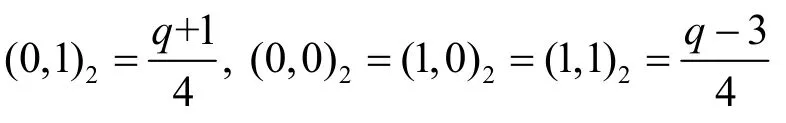
由前述記號，在上定義周期為(q-1)的SLCE序列{si}如式(1)所示。

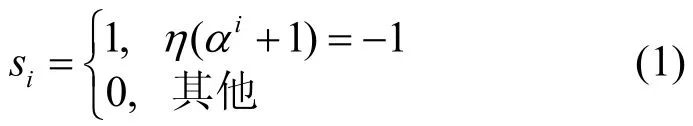
稱序列{si}為SLCE 序列。這個定義等價于

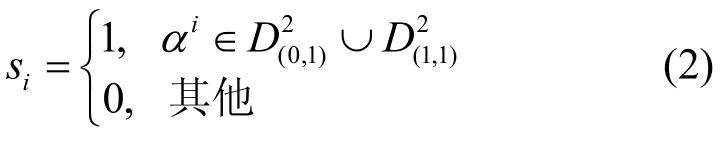
也等價于

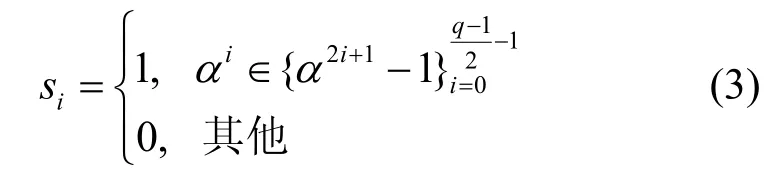
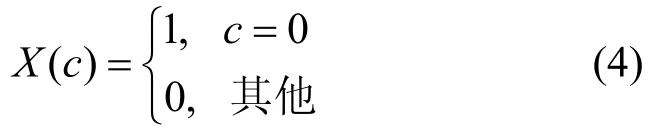
根據式(2)，在有限域F31中取本原元α=3，d=2，則有

進而可得一個周期為30 的SLCE 序列如式(5)所示。

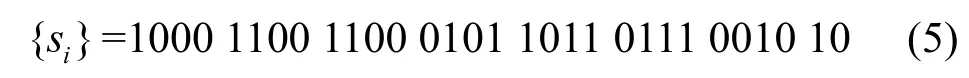
2.2 FCSR 和序列的2-adic 復雜度

考慮到線性移位寄存器容易被攻擊的問題，Klapper 等[12]提出了自帶進位的反饋移位寄存器(FCSR)。FCSR 由r個系數qi(i=1,2,…,r）∈(0,1),qr=1，以及一個初始存儲整數mn-1(可為任意整數)確定，結構如?圖1 所示。

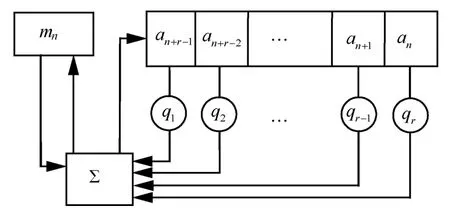
圖1 FCSR 結構

記FCSR 的任意一個狀態為 (an-1,an-2,…,ai,…,an-r)(ai∈{ 0,1},i=n-1,n-2,…,n-r)，存儲整數為mn-1，其運算如下。

2)右移一位，輸出最右端的an-r。

3)將a n=δn(mod2)放入FCSR 最左端。

每一個最終周期序列都可以由一個 FCSR 產生。反過來，所有由FCSR 生成的序列也都是最終周期序列[12]。設為最終周期序列，q為生成的FCSR 的連接整數，則稱q為的極小連接整數，極小連接整數整除任意連接整數。FCSR 序列的周期完全由其極小連接整數確定。類似于線性復雜度，2-adic 復雜度衡量一個周期序列需要用多大周期的FCSR 來生成，定義如下。

定義 1[12]設s={si}為嚴格周期序列，其中，q為序列s的極小連接數，整數p滿足gcd(p,q)=1，稱實數?(s)=lbq為序列s的2-adic 復雜度。

2-adic 復雜度衡量一個二元序列由帶進位的移位寄存器(FCSR)[12-13]生成的難度，它與線性復雜度沒有必然聯系。具有高線性復雜度的序列的2-adic復雜度可能會很低，反之亦然。Klapper 和Goresky[12]提出了有理逼近算法，即對于一條固定序列，只要已知其約為2-adic 復雜度個位置上的元素的2 倍，就能唯一確定原序列。這就要求密鑰序列必須具有高的2-adic 復雜度，才能有效抵抗有理逼近攻擊。

設s為嚴格周期序列，記則有，故

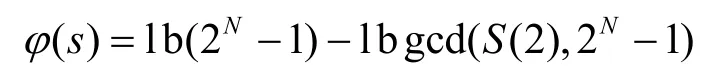
當gcd(S(2),2N-1)=1時，?(s)達到最大值l b(2N-1)≈N。

巧合的是，2N-1=MN恰為第N個Mersenne數，當MN為 Mersenne 素 數 時，有gcd(S(2),2N-1)=1，即序列s的極小連接整數為Mersenne 素數時，其2-adic 復雜度達到最大。迄今，已發現的Mersenne 素數有51 個，分別為N=2,3,5,7,13,17,19,31,61,89,107,127,521,607,1 279,2 203,2 281,3 217,4 253,4 423,9 689,9 941,11 213,19 937,21 701,23 209,44 497,86 243,110 503,132 049,216 091,756 839,859 433,1 257 787,1 398 269,2 976 221,3 021 377,6 972 593,13 466 917,20 996 011,24 036 583,25 964 951,30 402 457,32 582 657,37 156 667,42 643 801,43 112 609,57 885 161,74 207 281,77 232 917,82 589 933。由于第N個Mersenne 數為素數的必要條件是N為素數，因而對素數周期序列，當周期N滿足2N-1 為素數時，序列2-adic 復雜度達到最大。

對一般周期序列，2-adic 復雜度由gcd(S(2),2N-1)確定，這依賴于序列本身的性質。Tian 等[13]研究了m序列的2-adic 復雜度，利用m序列極小多項式的特征，推導出m序列可以達到最大2-adic 復雜度。Xiong 等[14]通過對周期序列的循環行列式非奇異性的研究，指出任何周期為N的理想二值自相關序列的2-adic 復雜度就是N，該結果覆蓋了文獻[13]的結果。Hu 等[15]對文獻[14]的結果給出了一個簡化的證明，給出了獲得周期序列2-adic 復雜度的新方法。

3 SLCE 序列的自相關性

設{si},i=0,1,…,n-1，為二元序列，稱函數

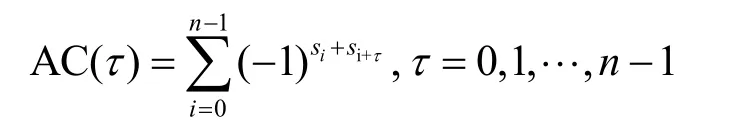
為該序列的自相關函數。周期為n的序列{si}的自相關函數可用差集表示為[16]

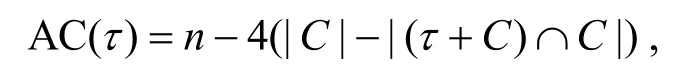
其中，集合C={i|si=1,i=0,1,…,n-1}為序列{si}的支撐集。

由于SLCE 序列為周期為(q-1)的平衡序列，其自相關函數滿足

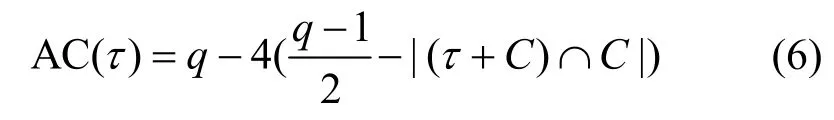
自相關函數值反映了序列在移位τ后，與原序列的接近程度。實際應用中希望序列的自相關函數值盡可能小。

設q為奇素數的冪，即q=pm，記Fq為q元有限域，α乘法群的本原元。記

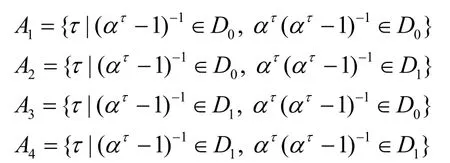
定理1設{si}是周期為(q-1)的SLCE 序列，則

1)當q≡ 1(mod4)時，

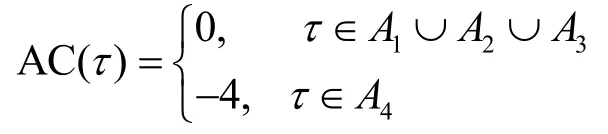
2)當q≡ 3(mod4)時，

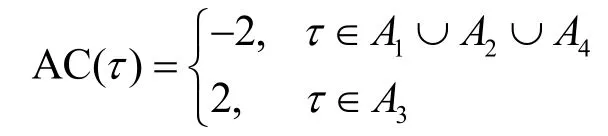
證明根據式(1)，需計算|(τ+C)∩C|，定義αC={αi:i∈C}=D1-1，及αC+τ=ατ(D1-1)，則有

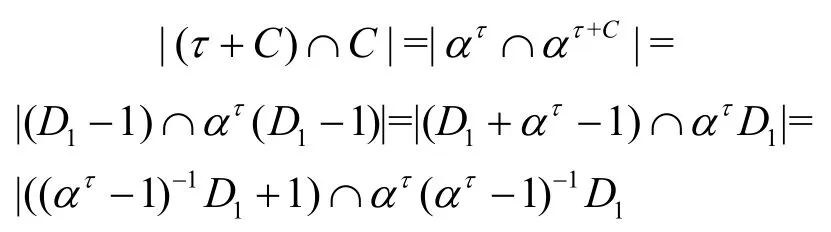
由引理1 和式(1)可得

1)當q≡ 1(mod4)時，若τ∈A1∪A2∪A3，則有

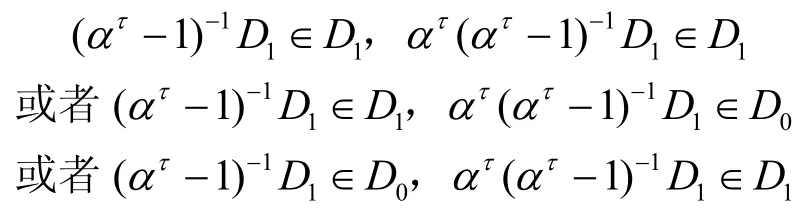
對應的|(τ+C)∩C|分別等于二階分圓數(1,1)2、(1,0)2和 (0,1)2，且都等于根據式(6)有

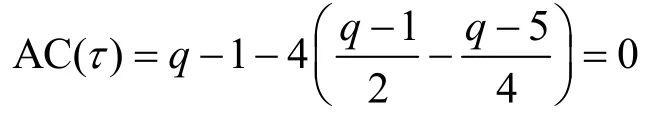
若τ∈4A，則有

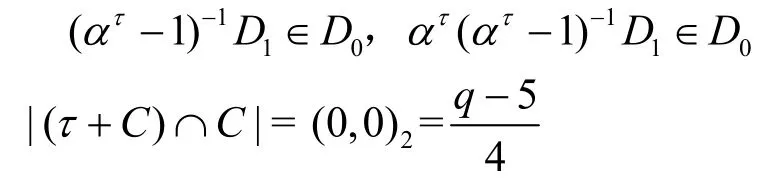
于是

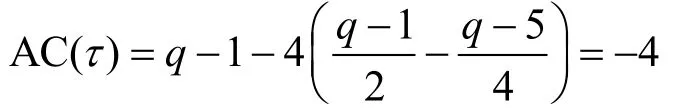
2)當q≡ 3(mod4)時，若τ∈A1∪A2∪A4，則有

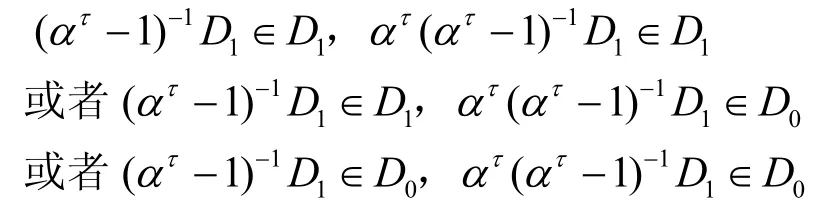
對應的|(τ+C)∩C|分別等于 (1,1)2、(1,0)2和(0,0)2，且都等于。根據式(6)有

若τ∈3A，則有

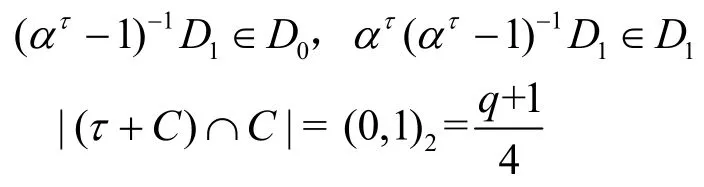
于是

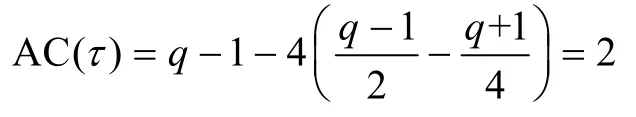
證畢。

定理1 表明SLCE 序列是3 值自相關序列。

推論1設{si}是周期為q-1的SLCE 序列，則

1)當q≡ 1(mod4)時，在τ=1,2,…,q-2中有個數使AC(τ)=-4 。

2)當q≡ 3(mod4)時，在τ=1,2,…,q-2中有的數使AC(τ)=2。

由分圓數的取法可證明推論1。

定義2若序列{si}、{tj}均為周期為N的序列，并且在一個周期上有si=tN-1-i,i=0,1,…,N-1，則稱{si}、{tj}為互反序列。

定理2記?為歐拉函數，域Fq中共有?(q-1)個SLCE 序列，并成對為互反序列。

證明由qF中本原元的個數為?(q-1)可得,由于在有限域中，當α為本原元時，α-1也為本原元，故?(q-1)個本原元成對出現。由于對本原元α，時，故α-1生成序列的第i個元與α生成序列的第(q-1-i)個元一樣，即為互反序列。

證畢。

定理3設{si}是周期為(q-1)的SLCE 序列，則

1)當q≡ 1(mod4)時，Fq上的全部SLCE 序列共有個自相關譜。

2)當q≡ 3(mod4)時，F q上的全部SLCE 序列共有個自相關譜。

證明記α為Fq的一個本原元，當q≡1(mod4)時，-α也是Fq的一個本原元，且有，故α與α-生成序列的自相關譜相同。又由自相關函數的對稱性及α與α-1生成序列為互反序列可知，α與α-1生成序列的自相關譜相同。于是α、-α、α-1、-α-1生成的序列同自相關譜。并且由其他本原元生成序列不同可得，當q≡ 1(mod4)時，F q上的全部SLCE 序列共有個自相關譜。

當q≡ 3(mod4)時，對本原元α、-α不是本原元，由前述知，此時Fq上的全部SLCE 序列共有個自相關譜。

證畢。

下面研究SLCE 序列的2-adic 復雜度。

4 SLCE 序列的2-adic 復雜度

定理4設{si}是周期為(q-1)的SLCE 序列，則

1)當q≡1(mod4)時，

2)當q≡ 3(mod4)時，

證明設{si}為SLCE 序列，記Z[x]多項式為

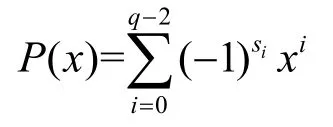
則有

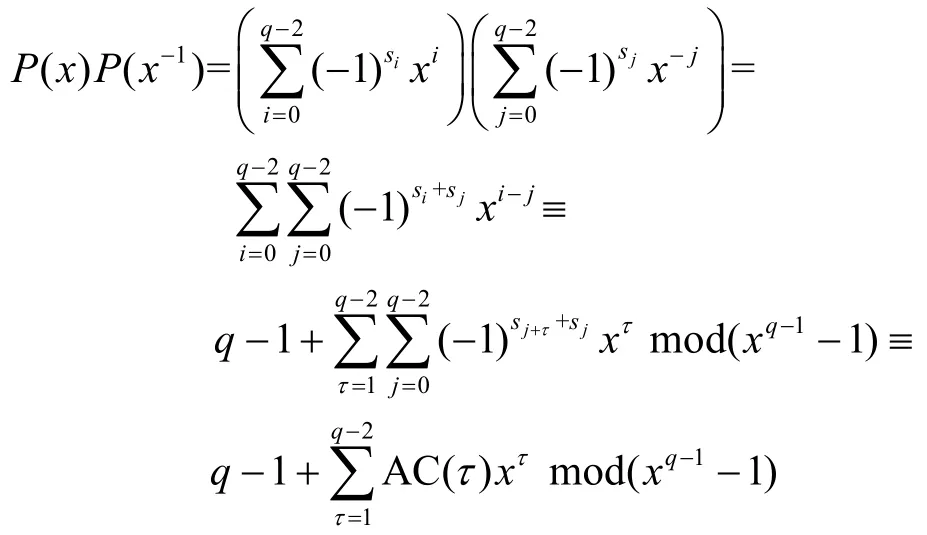
當x=2 時，有

其中，k為整數。于是

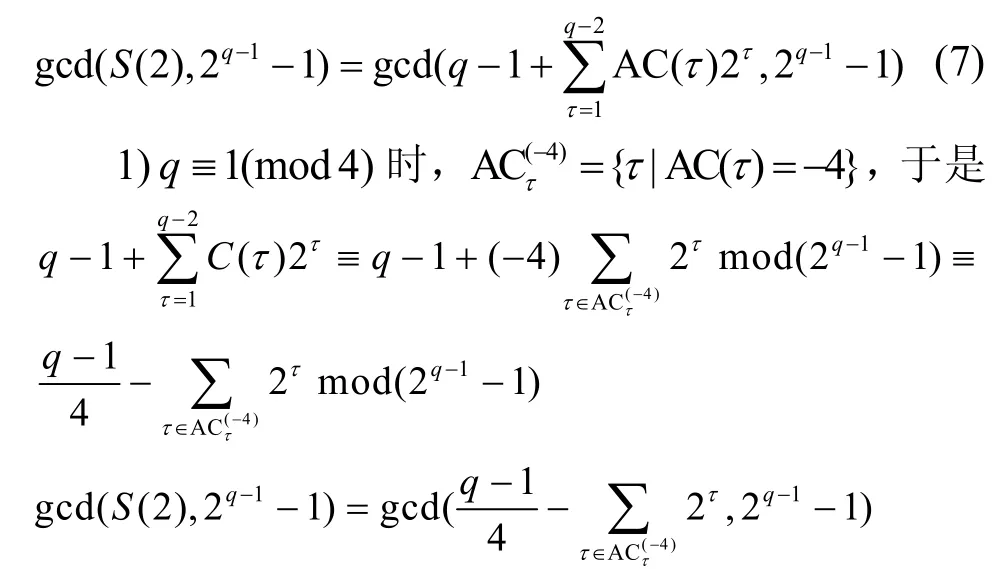
證畢。

推論2 設s={si}是周期為q-1的SLCE 序列，記，有

1)若q≡ 1(mod4)且

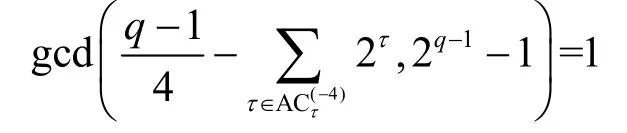
則s的2-adic 復雜度?(s)達到最大值。

2)若q≡ 3(mod4)，且

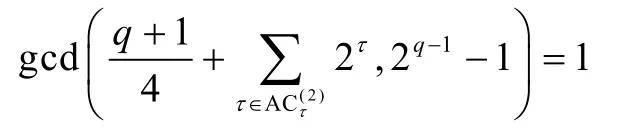
則s的2-adic 復雜度?(s)達到最大值。

推論2 的證明由定理4 易得。

進一步，當q≡ 1(mod4)時，有

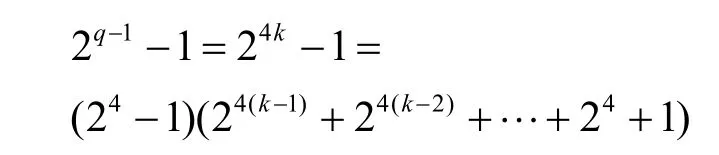
當q≡ 3(mod 4)時，有

例q=43時，F43上的本原元分別對應3,29,5,26,12,18,19,34,20,28,30,33。由本原元3 生成的SLCE 序列為1,0,0,1,1,1,1,0,1,1,0,0,1,0,1,0,0,1,0,1,0,0,0,0,0,0,0,1,1,1,1,1,0,0,1,1,1,0,1,0,0,1。，且有

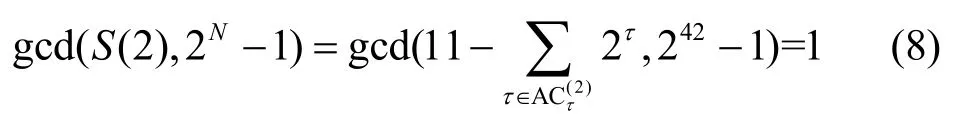
由本原元5 生成的SLCE 序列為1,0,1,0,0,1,0,0,0,0,0,0,1,1,1,0,0,1,1,0,1,0,1,1,1,0,0,1,1,0,1,1,0,1,0,1,0,0,0,1,1,1,，且有式(8)成立。

由本原元26 生成的SLCE 序列為1,1,1,1,0,0,0,1,0,1,0,1,1,0,1,1,0,0,1,1,1,0,1,0,1,1,0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,，且有式(8)成立。

由本原元29 生成的SLCE 序列為1,1,0,0,1,0,1,1,1,0,0,1,1,1,1,1,0,0,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,1,1,0,1,1,1,1,0,0],且有式(8)成立。

由Magma 驗證發現，F43中的所有SLCE 序列都達到最大2-adic 復雜度。類似地，F7、F19、F31、F47等域上的SLCE 序列都可達到最大2-adic 復雜度。但等域上的SLCE 序列都滿足gcd(S(2),2N-1)=3。盡管沒有達到最大2-adic復雜度，但由可知，在N＞4 時,這樣的SLCE 序列仍有很高的2-adic 復雜度。

5 結束語

SLCE 序列已被證明具有高線性復雜度，其2-adic 復雜度取值成為有意義的問題。本文通過SLCE 序列的自相關函數值研究了其2-adic 復雜度，給出了SLCE 序列可以達到最大2-adic 復雜度的一個充分條件，并舉例證明確實存在大量能達到條件的SLCE 序列，這些SLCE 序列能夠抵抗有理逼近攻擊，結合SLCE 序列高線性復雜度[3-6]可知，這些SLCE 序列是密碼學意義上的好的偽隨機序列。