多用戶FDD大規模MIMO下行系統能效功率分配算法
郭 慧,楊少川,張松煒,王 毅,2*
(1.鄭州航空工業管理學院 智能工程學院,河南 鄭州 450046;2.國家數字交換系統工程技術研究中心,河南 鄭州 450002)
0 引言
為了滿足無線傳輸在容量、速率、廣域覆蓋以及多樣化業務等方面的需求,無線通信設備的能量消耗迅猛增長,這使得運營商的成本支出也大幅攀升,而更為重要的是,越來越多的無線設備能量消耗對全球溫室氣體效應也造成了巨大壓力[1-2]。正因為如此,以能效為設計準則的綠色通信理念吸引了學術界和工業界越來越多的關注,也成為未來無線通信系統的主流發展趨勢[3-4]。綠色通信以單位功耗下的傳輸速率為衡量指標,由傳統的單一追求速率最大化或功率最小化為設計準則[5-6],轉向兼顧速率性能與功率消耗的折中設計[7-10],在追求高速率的同時盡可能降低功率消耗,從而達到能量利用率的最大化,以減少對環境造成的影響。
近年來提出的大規模多輸入多輸出技術(Multiple-Input Multiple-Output,MIMO)通過開發大維天線陣列空域資源,配備數十根到上百根天線,在不增加額外時域、頻域和功率域資源的前提下,可有效提升頻譜效率、降低發射功耗、減輕多用戶間干擾、簡化上層調度等等[11-12]。因此,大規模MIMO技術也被業內給予厚望,在5G移動通信系統的關鍵性能指標實現過程中扮演了重要的角色[13-14]。
現有蜂窩移動通信系統中大都采用FDD雙工制式[15],而針對FDD大規模MIMO系統的研究大多關注于下行導頻(也稱為訓練序列)開銷分析、導頻信號設計以及低開銷反饋量化方案等[16-18]。這主要是因為FDD制式中上下行信道不再滿足互易性,信道估計需要由基站向下發送導頻,再由用戶向上反饋,這一信道信息獲取方式會導致導頻和反饋開銷隨基站天線數的增加而大幅增加。盡管導頻開銷在信道信息獲取過程中十分重要,但是導頻信號的功率也決定了信道估計的精度。特別是,有效數據信號的功率直接關系著通信系統最終的速率性能,以及由此帶來的用戶間干擾量級。此外,導頻功率和數據功率還影響著整個系統的總功率消耗,而在能效準則下對導頻功率和數據功率的分配問題尚未深入研究。最新的文獻[19]研究了FDD大規模MIMO系統下行導頻與功率資源分配問題,但是該模型只考慮簡單的單用戶場景,并未考慮實際的多用戶模型。文獻[20]研究了TDD制式多用戶大規模MIMO系統的能效資源分配問題,但其主要考慮的是理想信道估計條件。而在實際的多用戶通信系統中,特別是存在估計誤差的信道信息條件下,用戶間干擾會變得更為復雜,這些會對解決能效準則下的功率分配問題帶來諸多困難。
基于此,本文考慮非理想信道狀態信息條件下的FDD制式多用戶大規模MIMO下行系統,解決能效設計準則下的基站下行訓練序列信號和數據信號功率分配問題。建立以能效為目標函數,導頻功率和數據信號功率為變量的優化問題,求解滿足最優能效目標下的最優發射功率解。最后,通過數值仿真對所提出的功率分配算法進行驗證。
1 系統模型與問題描述
1.1 FDD下行系統及傳輸過程建模
如圖1所示,考慮一個單小區FDD制式大規模MIMO系統。該系統由一個基站和M個用戶組成,基站配備大規模天線陣列,各用戶配置單天線,且基站天線數為N(N?M>1)。在FDD制式中,為了傳輸下行數據,需要先進行下行信道估計,再通過上行信道反饋估計信息,最后采用一定預編碼方案進行數據發送。為便于分析,此處假設上下行信道為瑞利平坦衰落,且信道相干間隔為Tc(以符號長度計),即在相干時長內信道系數近似不變。
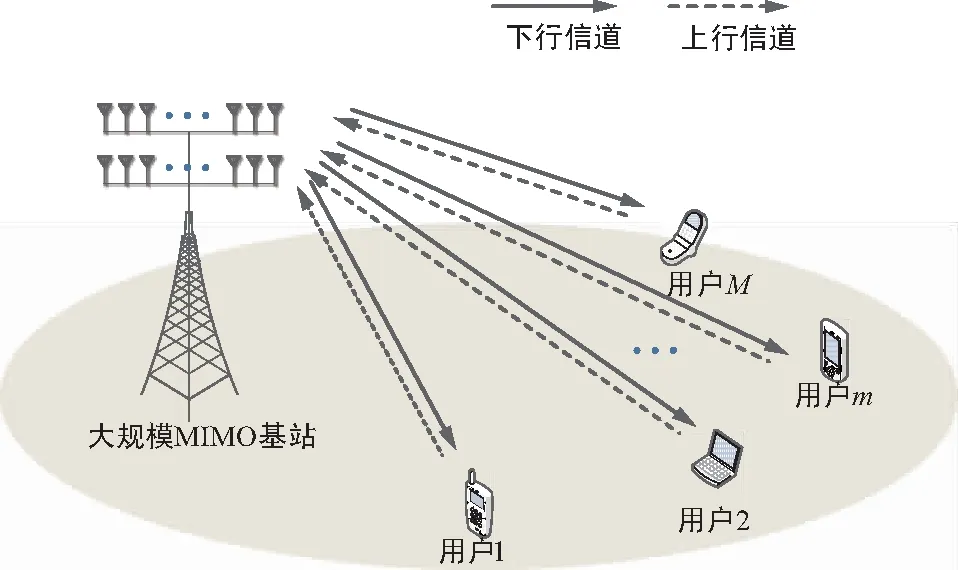
圖1 FDD多用戶大規模MIMO系統
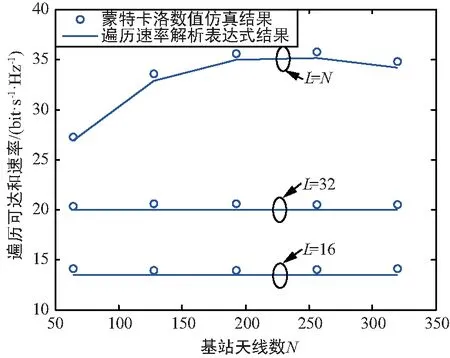
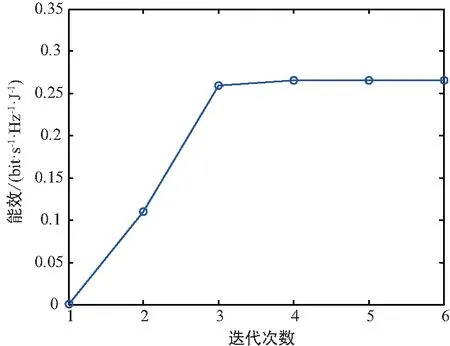
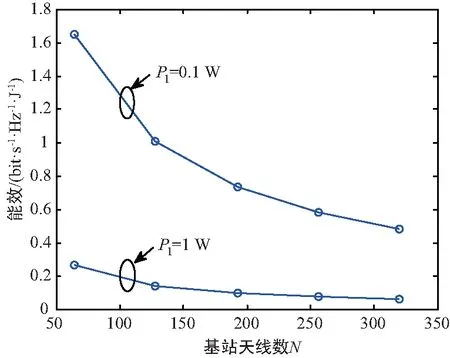
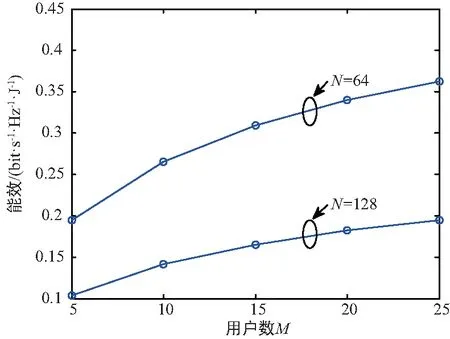
首先,基站使用前L( (1) 式中,Yp=[yp,1,yp,2,…,yp,M]∈L×M,且yp,m為第m個用戶接收到的導頻信號,pp表示訓練序列矩陣的每一列信號的平均發射功率,H=[h1,h2,…,hM]∈N×M為基站到各用戶的下行信道向量所組成的信道矩陣,hm(m=1,2,…,M)為基站到第m個用戶的下行信道系數向量,hm的各個元素為服從獨立同分布的零均值單位方差循環對稱復高斯隨機變量,即hm~CN(0,IM),Np=[np,1,np,2,…,np,M]∈L×M表示在下行信道估計階段各用戶端的零均值單位方差加性復高斯白噪聲,即np,m~CN(0,IL)。通常各用戶隨機分散在小區內部,因此,基站到不同用戶之間的信道系數向量滿足統計獨立性。 由于各個用戶地理位置的分散性,用戶間一般無法進行協作處理,各用戶需要獨立完成下行信道估計和數據解調。因此,第m個用戶利用其接收到的導頻信號yp,m對下行信道向量hm進行估計。此處,假設各用戶采用最小均方誤差(Minimum Mean Squared Error,MMSE)估計器,根據MMSE估計算法[21-22]可以得到hm估計值為: (2) (3) 顯然,導頻序列長度L與導頻功率pp直接影響著信道估計信息的精確程度。 在基站得到下行信道狀態信息后,采用大規模MIMO系統中普遍使用的最大比發送(Maximum Ratio Transmission, MRT)預編碼進行下行數據傳輸,MRT預編碼可在算法復雜度和性能之間處于較好的折中[12]。因此,基站發送的下行數據信號向量具有如下形式: (4) 式中,x=[x1,x2,…,xM]T為基站向M個用戶發送的下行數據符號向量,且該數據向量具有歸一化功率{‖x‖2}=IM,(·)T表示轉置運算,表示下行信道矩陣的估計值,θ表示基站對每個用戶的下行數據的平均功率歸一化因子[21],即滿足{‖s‖2/M}=1或‖·‖表示Frobenius范數。由此可得: (5) 式中,Tr{·}表示矩陣求跡運算。 由于各用戶對接收到的下行數據信號采用獨立解調譯碼,因此,第m個用戶的接收數據信號為: (6) 式中,pd表示基站發送的下行有效數據的平均發送功率,nd,m~CN(0,1)為下行數據發送階段在第m個用戶處疊加的復高斯白噪聲。根據最差情況不相干加性噪聲理論[21],根據式(6)可以得到第m個用戶的遍歷速率Rm為: Rm={lb(1+γm)}= (7) 式中,γm表示下行數據傳輸階段第m個用戶的等效接收信干噪比,|·|表示求模運算。考慮到信道估計開銷,需將Rm乘以系統資源維度損失因子,即(1-L/Tc)Rm。最終,可以得到所有用戶的下行遍歷可達和速率為: (8) 通過上述分析可以看到,導頻信號功率關系到信道信息獲取的質量,進而影響著預編碼矩陣與實際信道矩陣的匹配效果,而數據發送功率直接決定了有效傳輸速率,也與用戶間干擾程度有著密切關聯,二者的作用最終通過系統的遍歷可達速率反映出來。 整個系統的功率消耗主要由兩部分構成:射頻信號發射功耗和系統電路功耗[19]。在本系統中,信號發射功耗又包括導頻信號功耗和數據信號功耗,電路功耗則是指的維持系統運行時的固定功耗。因此,在一定時間內系統的總能量消耗可以表示為[19]: P=μppL+μMpd(Tc-L)+Tc(NP1+P2), (9) 式中,μ≥1為射頻功率放大器的功率轉換損失因子,P1表示基站端每根天線的射頻電路功耗,P2表示各電路模塊的靜態功耗,且P2與信號發射功率和天線數均無關。 基于綠色通信的設計要求,系統能效函數定義為遍歷可達速率與能量消耗之比[19]: (10) 因此,以最大化能效函數為目標,建立以導頻信號功率和數據發射功率為變量的數學優化模型, (11) 從式(7)和式(11)中可以看到,目標函數的分子形式非常復雜,其解析表達式難于求解,并且目標函數是分式形式,通常為非凸的。因此,該優化問題無法直接利用已有的凸優化方法直接求解。 對于式(11)中優化問題的目標函數解析表達式,主要難點在于求解分子上的遍歷速率Rm的閉合表達式。此處,利用大規模MIMO系統天線數量巨大這一特征,并采用大維隨機矩陣理論中的確定性等價近似方法[24],可以得出遍歷速率的一種有效近似解析表達式,有如下引理。 引理1:基站獲得下行信道估計信息后,采用MRT預編碼發送下行數據,在基站天線數N→∞時,可以得到第m個用戶遍歷速率的漸進極限閉合表達式: (12) 證明:由文獻[24]中引理1可知,當天線數N趨于無窮大時,可以得到式(7)中γm的分子分母各項極限值為: (13) 將式(13)中各極限值替換式(7)中的各項,通過化簡合并,便可得到γm的確定性極限值為: (14) 進一步,由文獻[21]中的主導收斂和連續映射理論可以得到Rm的確定性極限值為: (15) 證畢。 盡管定理1中給出的遍歷速率解析表達式是基于天線數趨于無窮大時所得到的極限形式,但是,該表達式在有限維度的系統參數配置條件下可以對遍歷速率進行較好的近似[21,23],通過仿真結果可以看到式(15)中的遍歷速率解析表達式與蒙特卡洛仿真值具有良好的逼近效果。 (16) 2.2.1 非凸問題近似轉化及全局最優解存在性證明 (17) 式中,除了變量(pd,pp)之外,其余參數均為正常數。利用文獻[25]中引理1的證明方法,可以得到能效函數η(pd,pp)關于其自變量的如下函數性質: ① 給定數據信號功率pd,η是關于pp的嚴格擬凹函數,且η隨pp增加呈現先增后減的變化趨勢; ② 給定導頻信號功率pp,η是關于pd的嚴格擬凹函數,且η隨pd增加呈現先增后減的變化趨勢。 基于上述2個性質,可以證明式(17)中優化問題存在唯一的全局最優導頻功率和數據功率,有如下定理。 (18) 證明:定義能效函數η(pd,pp)對應的α-上水平集Sα={pd,pp≥0|η(pd,pp)≥α},由文獻[26]中引理1的證明過程可知,當且僅當Sα在α取任意實數值時均為嚴格的凸集,則能效函數η(pd,pp)是嚴格的擬凹函數。下面,分別針對α取不同值時,對Aα的凹凸性進行判斷。 若α<0,則無法找到滿足η(pd,pp)=α的點。若α=0,則只有當(pd,pp)取(0,0)時才可使得η(pd,pp)=α。因此,η(pd,pp)在α≤0時是嚴格凸的。若α>0,首先將Sα變換為如下所示的等價形式, (19) (20) (21) (22) 式(21)和式(22)中的分母項P2顯然大于零,化簡后可以得到: (23) (24) (25) 2.2.2 最優解閉合表達式推導及算法流程描述 從式(18)可以看出,最優導頻功率與最優數據信號功率之間滿足線性比例關系,且該常系數僅由系統用戶數、導頻長度以及信道相干時長所共同決定。盡管式(18)中最優功率變量具有簡單的線性關系,但要直接求解式(17)的優化問題,特別是求解得到最優解的閉合形式十分困難。為了解決該問題,將式(18)代入式(17),將優化問題進一步轉換為單變量的優化問題, (26) 為了求解式(26)中的優化問題并獲得閉式解,根據分式規劃的性質[27],可將原優化問題轉換為具有減法形式的等價優化問題,再通過交替迭代的優化方法進行求解。定義關于能效變量η的函數G(η): (27) 根據文獻[9]中定理1可知,G(η)=0有且僅有一個零根,且該零根就是式(26)中優化問題的最優能效值ηopt。因此,當式(27)中取ηopt值時,所獲得的最優功率解就是式(26)中優化問題的最優解。盡管事先不知道ηopt的具體值,但可以通過Dinkelbach方法[27],進行兩層交替迭代,求解得到最優能效值和最優功率值,即先給定能效值η,求解最優功率解pp,再用功率值pp更新當前能效值η時算法收斂。因此,求解最導頻功率值的關鍵在于求解如下優化問題: (28) 利用標準的凸優化方法[28],將式(28)中目標函數對自變量pp求一階導數,并令其為零,化簡后可以得到: (29) 根據求根公式,直接得到最優導頻功率的閉合形式解: (30) 由以上分析可知,在多用戶FDD大規模MIMO下行系統中,可根據靜態的系統參數(如用戶數、導頻長度、信道相干間隔以及射頻功率損耗因子等),對基站下行導頻功率和數據功率進行分配,從而獲得最優能效性能。同時,本文算法中僅有標量運算,具有較低的復雜度。 最終,可以得到基于能效最大化的功率分配算法具體步驟流程。 1.輸入:能效初始值η0>0,迭代次數i=0,收斂精度ε>0 2.Repeat 3.基于ηi,利用式(30)獲得最優導頻功率值pp,i; 4.利用pp,i,更新能效值 5.更新迭代次數i=i+1; 對于本算法的收斂性證明可參考文獻[20]和文獻[27]中的類似過程直接得到,此處不再贅述。 本節通過數值仿真對所提出的能效最大化功率分配算法進行驗證并分析性能。仿真中所用到的系統公共參數設置如下:基站到每個用戶的路徑損耗因子為1,信道相干間隔Tc=1 000(它對應于200 kHz的信道相干帶寬和5 ms的信道相干時間),信道估計與數據傳輸階段的加性高斯白噪聲功率均歸一化為1 W,基站發射機功率損耗因子μ=1,基站節點中各電路模塊的靜態功耗P2=1 W,迭代算法收斂精度ε=10-8。 通過蒙特卡洛數值仿真驗證引理1中給出的遍歷可達速率解析表達式精確性,并在訓練序列長度L取不同值時,觀察遍歷可達和速率的變化情況,其中,蒙特卡羅數值仿真是通過生成5 000次獨立信道系數條件下再求平均得到。圖2中設置用戶數M=10,導頻信號功率和數據信號功率為pd=pp=10 W。從圖中可以看出,引理1給出的遍歷速率解析表達式理論值與蒙特卡洛數值仿真值具有良好的逼近性能。當訓練序列長度L固定為16或32時,遍歷可達和速率出現飽和狀態,這是由于用于信道估計的導頻序列長度固定后,信道估計精度無法提高出現平臺效應,從而天線數的增加并不會對遍歷速率帶來更多的性能提升。而當訓練序列長度隨天線數增加時,即L=N,可以看到遍歷可達和速率出現先增后減的趨勢。這是由于訓練序列長度增加,保證了信道估計精度,大規模天線陣列所帶來的分集復用增益大于系統信道估計資源開銷損失,而當訓練序列增加到一定程度時,在有限的信道相干間隔內,信道估計開銷大幅增加,從而大規模MIMO帶來的速率提升無法彌補信道估計開銷帶來的系統資源損失,出現了性能下降。 圖2 下行遍歷可達和速率在不同導頻長度設置下的性能 圖3給出了當系統參數為M=10,L=32,P1=P2=1 W時,本文所提出的迭代優化算法的收斂軌跡,從圖中可以看到大約4次迭代之后,能效值便基本達到了穩定狀態,這也說明了本文所提出的算法具有較好的收斂速度,復雜度較低。 圖3 迭代優化算法的收斂軌跡 圖4給出了當系統參數為M=10,L=32時,最優能效值隨基站天線數的變化趨勢,并在每天線電路功耗不同時,對比了最優能效值的差別。從圖中可以看到,隨著天線數的增加,最優能效值是持續下降的。對于該現象,從式(17)中可以分析得到,由于采用了固定的訓練序列長度,基站天線數只影響到能效函數分母的總能耗,因此,當增加基站天線數時,能效值勢必會降低。當每天線電路功耗從1 W降為0.1 W時,可以看到最優能效值大幅提升,特別是在天線數相對較少時,這主要是由于基站天線射頻電路功耗大幅降低,從而降低了總的能量消耗,提升了系統能效性能。 圖4 在不同的每天線電路功耗條件下,最優能效性能隨基站天線數的變化趨勢 圖5給出了當系統參數為L=32,P1=P2=1 W時,隨用戶數增加時,在給定的基站天線數條件下,最優能效值的變化趨勢。從圖中可以看到,隨著用戶數的不斷增加,最優能效值呈現遞增趨勢,這一性能提升主要得益于多用戶復用增益,提升了能效性能。 圖5 在不同的基站天線數條件下, 最優能效性能隨用戶數的變化趨勢 本文研究了基于能效最大化的下行信道估計和數據傳輸兩階段的功率分配問題,考慮到信道估計誤差和多用戶間干擾影響,獲得了一種低復雜度的功率分配迭代算法,并推導得到了最優功率的閉合形式解。從該閉合形式解中可以看到,最優導頻功率和最優數據功率均只與系統靜態參數相關,而與信道瞬時信息無關,且二者之間為常系數線性關系。通過計算機仿真,驗證了該功率分配算法實現最優能效目標的有效性。從仿真結果中發現,當系統導頻序列長度固定時,持續增加天線數會大大降低系統的最優能效性能,這主要是由于導頻長度固定后,系統可達速率與天線數不再具有遞增關系,而能耗卻隨天線數倍增,從而導致最優能效遞減,這與TDD制式下的能效變化趨勢大為不同,其根本原因在于兩種制式下導頻開銷和信道估計模式的不同。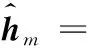
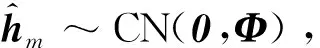
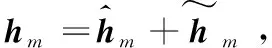
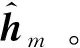

1.2 能效函數定義及功率分配問題
2 基于能效最大化的功率分配算法設計
2.1 遍歷速率解析表達式
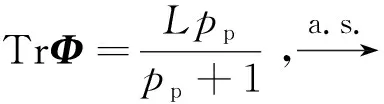
2.2 優化問題求解
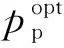
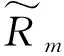

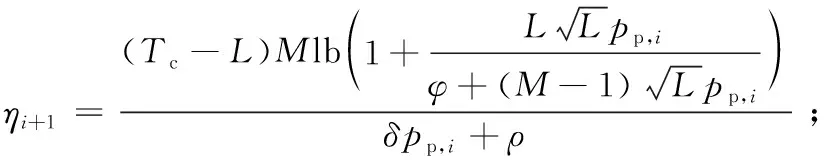

3 仿真結果與分析
4 結束語

