生活味，讓數學課堂更生動

江蘇省昆山震川高級中學 馬玉紅

在數學學習中，學生應該充分了解數學中的生活味，感受數學之美。教學中要將生活問題融入數學課堂教學中，讓學生體驗數學的魅力，提高學生解決數學問題的能力。

一、問題的探索

1.用一雙善于發現生活中數學的眼睛，提高學生發現實際數學問題的能力

數學課程標準的要求之一是情境教學，這要求教師有敏銳的觀察力，善于發現生活中的數學。讓數學課堂生活味，把現實生活中學生感興趣的事情進行加工、整理并運用到數學課堂中。

例如我在教學“數列的應用”時，就圍繞“今天我買房”這個主題：房價上漲，手中只有十萬元存款，現在需要買40 萬元的房子，準備貸款買房。我讓同學們到銀行了解情況后，第二天告訴我具體辦法。這樣，教科書中缺乏關系的問題更加生動，學生有參與的動力，變被動學習數學為主動學習。通過這種方式，學生可以更好地理解數學的作用，感受到使用數學的樂趣。

2.有一雙善于發現生活中數學的手，培養學生解決數學問題的能力

大部分學生在學習立體幾何時都覺得太抽象，想象不出來。講解立體幾何時，我就讓學生用硬紙板做生活中可以看見的立體圖形，讓他們對比自己手中的圖形去學習立體幾何性質，課后檢測時大部分同學都能準確掌握有關概念與性質。

案例：在直三棱柱ABC—A1B1C1中，AB=BC= ，BB1=2，∠ABC=90°，E、F分別為AA1、C1B1的中點，沿棱柱的表面從E到F兩點的最短路徑的長度為_______________。

在做這道題時，我提示學生把以前做的幾何體拿出來看看，剪剪試試，引導他們發現問題的實質，空間幾何體中，無論這兩個面夾角是多少度，兩個面內各取一點，沿著交線折起，長度是不變的。利用平面內兩點間直線的距離最短，這類問題就是把兩個平面展平。

我馬上把這個問題類比到圓錐上：一個圓錐的底面半徑10cm，高為8cm，一只螞蟻從底面圓上任意一點A出發，沿著圓錐的側面爬行一周回到A點，所走的最短路程是多少？學生馬上反應出來要將圓錐展開處理。

趁熱打鐵，拓展延伸到圓柱上：如圖，螞蟻從A點出發，沿著圓柱的側面爬行兩周到達B點，問最短距離是多少？

學生發現繞一圈是直接展開，兩圈應展開兩次。

再變形到：圓柱下表面封閉，母線和底面圓直徑長均為2，BC中點P，在圓柱內壁P處有一粒米，外壁A處有螞蟻，則螞蟻吃到米所經過的最小路程為多少？

剛開始學生有點迷糊，這再展開一次、兩次都沒用，我給了提示：如果把容器看成是有內外兩層的呢？學生馬上就明白了，就是展開再對稱。

以上三個題目是同一個道理，同學們發現動手能夠解決數學問題，數學就在他們身邊，同時，動手做出一件事物使得他們有一種成就感，享受成功的愉悅。通過自己動手操作獲取知識，激發了學生體驗數學生活的樂趣。

二、問題的解決

學生碰到生活中的問題會感覺到興奮，解決了會有一種成就感。那么，怎么解決好生活中的數學問題呢？并不是只停留在學生動手上，而是要利用已經掌握的數學知識去指導解決實際問題。

例如2010 年江蘇卷第17 題，這個數學應用問題難于將實際問題轉化為已經學過的數學，即把現實問題“數學化”。

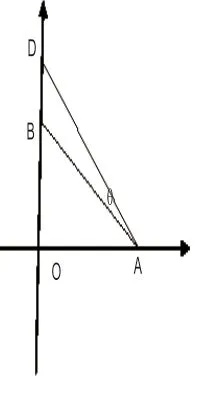
分 析： ①求α-β最 大， 難 點 在 于α-β= ∠DEB， 這 樣tan ∠DEB最大即∠DEB最大，即α-β最大。把問題數學化，問題常規化。

②聯系課本題求∠θ最大。

③問題推廣：世界杯射門問題：AB為球門，球員在哪個區域射門命中率最高？

以上兩個數學應用問題為同一題目，“數學化”后都可用②來解決。教學中，以上兩個問題的解決反映出來兩個問題：一是學生找不到切入口，即學生找不到問題的關鍵，不能把實際問題數學化；二是學生出不來，學生的計算能力較差，對最值問題處理不得當。所以在處理跟生活相關的應用問題時應該分為五個步驟：（1）審清題意；（2）建立數學模型；（3）用適當的方法進行計算；（4）檢驗答案是否符合實際意義；（5）作答。五個步驟中，學生最難攻克的是步驟（1），生活類應用題題目長，描述語言多，學生因為害怕而不愿意深思，抓不住重點，也就沒有辦法進入題目中，所以審題最重要，要先把題目縮減，長題變短，變成符合學生的口味，更容易建立數學模型。其次是步驟（3），應用題的表達式不像其他計算類題目式子那樣簡潔、有針對性，需要自己整理，一是學生沒有整理意識；二是學生有畏難情緒。在教學中應該適當演示計算步驟，讓學生掌握計算方法，會應用計算技巧，鼓勵學生堅持算到底，培養學生的意志力。

三、問題的反思

教師要善于將生活問題與數學知識融合，加入課堂教學中，引導學生分析、思考，在學生活動中總結數學知識，實施教學過程。積極創設豐富有趣的情境，讓學生體驗數學，分析和解決現實生活中的問題，這樣既能學好相關的數學知識，又能提高解決實際問題的能力。教師在課堂教學中引入的生活中的數學內容越豐富，課堂教學活動越生動，學生對數學學習更感興趣，生活中的數學是課堂數學活動的動力源泉。