小學數(shù)學“思動課堂”的實踐與思考

福建省泉州市實驗小學 陳 璐

一、為什么？——“思動課堂”的提出緣由

數(shù)學教學是數(shù)學活動的教學，這其中既有外顯的操作活動，更離不開內(nèi)隱的思維活動。但在日常教學中常見以下現(xiàn)象：只見“活動”不見“數(shù)學”，學生“動而不思”，課堂上如走馬觀花，學習的過程浮于表面；只見“數(shù)學”不見“兒童”，為完成教學任務壓縮活動時間，學生“思動脫離”，學習的效果難以保證。如何創(chuàng)設有趣的情境，組織有效的活動，讓學生在生動的過程中獲得深刻的體驗，值得思考并嘗試。為此，我們依據(jù)新課程理念，聚焦學科核心素養(yǎng)，著眼學生的思維發(fā)展，致力于小學數(shù)學“思動課堂”的實踐與研究。

二、是什么？——“思動課堂”的內(nèi)涵解釋

“思動課堂”包含著“思”與“動”兩個方面。其一，“思”。“思”是內(nèi)在的、是隱性的，指思考、思想、思維等。數(shù)學教學要驅(qū)動思考、融入思想、發(fā)展思維。教師要創(chuàng)設合適的問題情境，激發(fā)學生主動思考，感悟數(shù)學思想，從而獲得思維的發(fā)展。其二，“動”。“動”是外在的，是顯性的，包括“五動”：口動（善于表達，學會對話）、手動（善于操作，學會合作）、耳動（善于傾聽，學會辨別）、腦動（善于思考，學會思維）、情動（善于理解，學會欣賞）。手動、口動、耳動即學生行為上要參與；腦動即學生思維上要參與；情動即學生情感上要參與。這里的“動”是多維的，是立體的，是多種感官共同作用之下的結(jié)果。學生的學習是“主動學習”，是一種“全身心參與活動”的狀態(tài)。

綜上可見，“思”遵循認知心理的規(guī)律，是“動”的本質(zhì)和目標；“動”遵循兒童心理的規(guī)律，“動”是“思”的形式和載體。“思動課堂”是關注生命情懷的課堂，是促進思維發(fā)展的課堂，體現(xiàn)了“三個突出”：突出學習的過程性。鼓勵學生“從頭到尾”地思考，經(jīng)歷解決問題的全過程；突出學習的探究性。引發(fā)學生的學習興趣，激發(fā)他們獨立探究，從不同角度的思考，在合作交流中共同建構(gòu)知識；突出學習的開放性。根據(jù)數(shù)學知識的內(nèi)在聯(lián)系，盡可能伸長“學習的觸角”，對所學知識進行適當拓展延伸，讓學生帶著新問題走出課堂。

三、怎么做？——“思動課堂”的教學實踐

“思動課堂”不只是理念，更應是實踐。如何將這種理念融入具體的實踐中，現(xiàn)以《三角形的分類》一課為例，提出幾點思考。

1.“動”中啟“思”——在操作與反思中學會認知的方法

知識是思維的產(chǎn)物，但反映在教材中時常是隱蔽不明的。教學中，教師要帶領學生對有關知識的產(chǎn)生過程進行合乎邏輯的思維模擬，再現(xiàn)數(shù)學知識的發(fā)生、發(fā)展過程，把數(shù)學知識的教學變成數(shù)學活動的教學。

本課教學中，先提供7 個三角形讓學生進行分類、交流。基于現(xiàn)實生活中三角形不計其數(shù)，怎樣讓學生從“窺一斑”而“見全豹”呢？教學中，筆者組織了以下兩個活動：①讓每位學生各自畫一個三角形，然后對照明晰它屬于哪一類，撬動學生的直接經(jīng)驗；②啟發(fā)思考：所有的三角形按角分，就只有這三類嗎？并提供相關“反例”（如兩個直角、一個鈍角等）讓學生聚焦思考。這一數(shù)學問題直接挑動了學生思維之弦，學生循思而動，通過畫圖驗證、推理排除等方法，主動自解心中的疑惑。這樣，學生不但經(jīng)歷了分類的全過程，積累了分類的經(jīng)驗：“標準統(tǒng)一，不重復，不遺漏”，同時，更體會到數(shù)學知識的邏輯性和嚴謹性，豐厚了研究數(shù)學問題的方法和經(jīng)驗。

2.“動”中明“思”——在分析與比較中建立清晰的表象

本節(jié)課涉及的知識點多，怎樣把它們統(tǒng)整起來、系列化起來，并且深刻化理解？教學中，筆者創(chuàng)設了有趣而有效的數(shù)學活動，激發(fā)學生開動思維的馬達，在互動中交流，在思辨中深入，在分析、比較中厘清概念之間的關系，讓知識結(jié)構(gòu)化、系統(tǒng)化。

在學生將三角形按角的特點分類，認識了銳角三角形、直角三角形、鈍角三角形后，進一步引導學生比較三者的異同，從而發(fā)現(xiàn)這三類三角形的名稱與其中最大的角相對應，幫助建立清晰的圖形表象。學生經(jīng)歷觀察、比較、發(fā)現(xiàn)等數(shù)學活動，思潮起伏、思緒激動：原來數(shù)學家們是利用“特征命名法”給三角形命名的！動中明思，感悟數(shù)學知識的“趣”與“妙”。此外，在將三角形按邊的特點分類，揭示等腰三角形的概念之后，及時讓學生動手比劃出“腰”在哪？學生邊動眼觀察、邊動手比劃，以思促動，直觀形象地感知等腰三角形的特征，并且在比劃中自然而然地體會等邊三角形是特殊的等腰三角形，明晰兩者的關系，完善認知結(jié)構(gòu)。

3.“動”中深“思”——在觀察與想象中獲得思維的發(fā)展

發(fā)展學生空間觀念的核心在于想象。立足于眼前，構(gòu)建于腦中，自由地轉(zhuǎn)化、推理。通過前面的學習，學生已初步建立不同種類三角形的表象，筆者設計了一個綜合運用的活動：①觀察判斷：圖1 中的三角形是什么三角形？②引導想象：A點向右移動，會變成什么三角形？向左移動呢？③交流思考：你是怎么想的？④幾何畫板動態(tài)演示，定格成圖2，繼續(xù)引導想象：如果A點向下移，又會變成什么三角形？

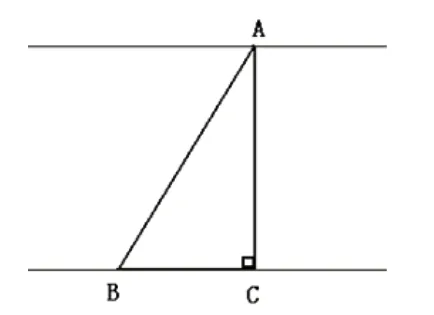
圖1

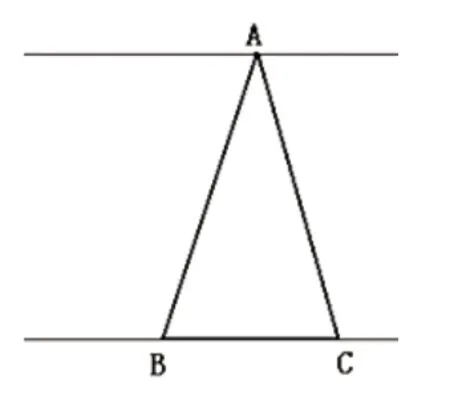
圖2

學生在此過程中需動眼觀察（三角形中A點的變化方向），動腦想象（A點移動變化后形成的三角形），動口表達（描述想象中的三角形，運用所學知識解釋是什么種類的三角形），動耳傾聽（同伴的想法與自己所思是否一致）。因思而動，動中深思，讓知識的學習伴隨著豐富的數(shù)學思考，從靜態(tài)走向動態(tài)，引領學生的思維向更高處拔節(jié)。