論數學教學過程中的教與不教

☉四川省成都雙流中學實驗學校 文傳福

數學教學活動需建構在學生的認知基礎和知識經驗水平之上.教師通過讓學生參與數學活動，引導他們通過自主探究、合作交流，理解和掌握數學知識和技能，滲透數學思想方法，從而獲取充分的數學活動經驗.新課改風向標下，教師在數學課堂教學中，需創設有效的教學情境，提出合理的問題，把控好“教與不教”的尺度，藝術性地處理好“教與不教”的矛盾，激發學生的探究意識，提高學生學習數學的興趣，讓數學學科核心素養在數學課堂上真正得以落實，從而提升教學質量.下面筆者就自身教學中的一些做法和感悟，與同仁交流.

一、教是為了不教

教學過程中，作為課堂教學的組織者和引導者，教師需創設恰如其分、行之有效的教學情境，啟發學生多方位、多角度地分析問題、解決問題，充分調動學生的學習積極性，讓學生的潛能在最大程度上得以發揮.所謂“教”，就是教師在教學中以啟發式引導，激發學生的主觀能動性，逐步滲透數學學習方法，激勵他們勇于發現、樂于思考、勤于探究，最終實現自主學習.

案例1：學生基本掌握運用直接開方法求解一元二次方程根的問題后，可以引導學生運用配方法求解二次項系數為1的一元二次方程.如果教學過程中，教師直接引入問題“如何求解方程x2-4x-5=0”，學生必定一籌莫展，不知從何下手.筆者創設了以下教學情境，引導學生思考，培養數學思維，啟迪學生發現和解決問題：

師：如何解方程（x-2）2=9？

生1：由（x-2）2=9，可得x-2=±3，則x=2±3.則x1=5，x2=-1.

師：很好.能否嘗試解方程x2-4x+4=9？

生2：可以看出x2-4x+4=（x-2）2，再將其轉化為以上同樣形式即可解決.

師：不錯.如何解方程x2-4x=5呢？

生3：只需在方程的兩邊同時加上4即可，即x2-4x+4=5+4.

師：那么如何解方程x2-4x-5=0？

生4：由x2-4x-5=0，得x2-4x=5，則x2-4x+4=5+4，則（x-2）2=9，則x-2=±3，則x=2±3，則x1=5，x2=-1.

師：我們再嘗試解方程x2-6x+8=0.

…………

之后筆者引導學生歸納解題方法，如下：

（1）先移動常數項至方程右側；

（2）再將方程兩側均加上一次項系數一半的平方，使得方程左側可化為完全平方式；

（3）最后直接用開方法求解.

通過有意識、有計劃的引導，激發學生自主發現和探究問題的興趣，從而促進學生積極、主動思考問題，形成正確解題路徑.

案例2：教師出示問題：小紅同學通過以下方法求解方程是否正確？請說明原因.

解方程：（x+2）2=4（x+2）.

解：方程兩邊都除以（x+2），可得x+2=4.

則x=2.

大部分學生都認為不正確，原因在于他們認為一元二次方程的解為兩個，并非上述解答中的一個.很顯然，這是依據表象進行的基本判斷.

師：我們可以思考一下，以上解題過程中，問題出在哪一個步驟上呢？

生1：當方程兩邊同時除以（x+2）時，會出現x+2=0的情況，所以這一步錯了.

師：回答得很好.

…………

借助情境的參與，激發學生自主思考和深度探究，讓學生在想象、發現、創造的過程中，打開思維空間，感受數學思想方法，提升思維的廣闊性和靈活性，培養學生的解題能力，進而提升教學效益.

二、不教也為教

教學中所謂的“不教”，是指對于一些學生可以借助自主思考、探究、合作討論得出結論的數學問題和數學知識，不需要直接講授，只需留足時間和空間，引導學生積極思考、自主探究、合作學習，進而解決數學問題.當然，這里所說的不教并不是“完全放養式”，而是恰到好處地教，讓學生通過學習數學知識，提升數學素養，創設高效課堂.

案例3：筆者在教完“平方根”后，借助以下教學情境導入“立方根”這一內容：

師：假設我們一起制作一個正方體紙盒，它的容積是27cm3，此紙盒的棱長是多少呢？

生（很快得出答案）：3cm.

師：我們再一起制作一個正方體紙盒，它的容積是15cm3，此紙盒的棱長是多少呢？

學生小聲討論，但得不到答案.

師：你們認為這個棱長是否存在？

生：肯定存在.

師：既然一定存在，是多少呢？該如何表示呢？

分析：從以上梯度式情境中引導學生進行對比，感悟出容積為15cm3的正方體紙盒是存在的，進而得出其棱長也是存在的.基于學生的已學知識“平方根”，繼續推進教學過程：

師：我們帶著這個問題去書本上找尋答案，通過書本內容回答以下幾個問題：

①什么是“立方根”？它的意思是什么？

②什么是“開立方”？8的立方根是多少？-125呢？

以上教學設計，一方面，使知識實現正遷移；另一方面，提升學生的閱讀理解水平.

案例4：筆者在教學“直角三角形全等的判定”第2課時時，為了引導學生感悟角平分線的性質及判定，提出以下問題：

如圖1所示，OC平分∠AOB，OC上有一點P，且PD⊥OA，D為垂足，PE⊥OB，E為垂足，求證：PD=PE.

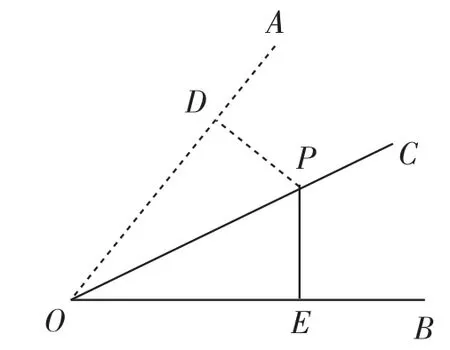
圖1

在解題過程中，學生自主觀察和思考，而后完整、順利地寫出了解題的過程，并歸納出以下性質：“位于角平分線上的任意一點到角兩邊的距離都相等.”筆者適時追問：“倘若我們將定理的條件和結論互換，也就是以下命題‘如果有一個點到一個角兩邊的距離相等，那么這個點一定在這個角的平分線上’，此命題是真命題嗎？能否證明？”此刻，學生興趣盎然，激發了火熱的思考、深度的合作探究、思想的碰撞，促進了智慧的生成，證明過程躍然紙上.讓筆者最為欣喜的是，整節課中學生自主參與學習過程，可以說深度思考真正實現了，學生的能力自然而然就形成了.

三、教與不教完美統一

在課堂教學中，教師作為學生學習行為的“創設者”，引導學生思考、發問，激發學生深入探究和深度思考.學生既是教學的“客人”，又是教學的“主人”，在學習中引發思考、主動參與、感悟成功，得到發展、促成智慧.所以，學生對教師有一定意義上的依賴性，又具有一定程度上的獨立性.課堂教學中，若離開了教師的“教”，學生就無法實現從不會到會，從無知到知，從不行到行，進而實現“不需教”的過程.當然，若離開了學生的“主動學”，主動參與、獨立思考、遷移運用所學知識，那么學習則僅僅是浮于表面，毫無深度，教師的“教”也是蒼白無力、毫無效果.只有兩者完美統一，才能滿足學生的求知欲、表現欲和發展欲，提升學生的思維能力，引導學生從數學思想的高度建構知識，進而獲得較好的教學效果.

多年的教學與實踐顯示，教學中需做到“有所教，有所不教”，將教與不教完美統一，才能消除教學中的機械重復，使教學過程生動、有趣，使學生由“學會”走向“會學”，充分調動學習的興趣，學會學習方法，培養學生自主學習的能力，從而實現終身享用.當然，對于學生自主學習能力的發展而言，教師還有很長的路要走，需要做到鉆研教材和探究學生的具體學情，并基于教材和具體學情，創設行之有效的教學情境，促進學生思維的發展.當然，有效的教學情境創設僅僅是其中的一個環節，掌握好“教與不教”的藝術才是關鍵，使數學課堂盡可能鮮活、生動，全面激活學生的思維，讓學生在自主、合作、探究的過程中，感悟數學知識，積累數學技能，促進數學學科核心素養的提升.