探尋概念教學支點 打好數學教學根基

■趙祝干

好的開頭是成功的一半。數學概念教學是每一章教學的基礎。筑牢根基，埋好章節教學的第一粒“種子”，是深化教學、系統教學、全面教學的前提。教師在概念教學中，萬不可走馬觀花，囫圇吞棗，應該多尋找支點，讓學生駐足停留，咀嚼玩味，練就火眼金睛、見微知著的本領。

一、文讀百遍，其義自見

進行數學概念教學前可先開展數學名詞解釋，用語文閱讀理解的方式切入主題，不失為一個好支點。先反復讓學生讀題目，細細品味概念的字面意義與實質意義。俗話說，書讀百遍，其義自見。例如“二次函數”的教學：

師：同學們，你能從字面上分析二次函數的概念嗎？

生1：有兩部分，形容詞“二次”，名詞“函數”。

師：那“函數”是什么意思？“二次函數”又是什么意思？

生2：在一個變化過程中的兩個變量x和y，如果對于x的每一個值，y都有唯一的值與它對應，那么我們稱y是x的函數，x是自變量。二次函數的意思就是自變量的最高次數是2。

師：同學們答得真好，看來你們的眼睛都是雪亮的。

研究性學習從題目開始。咬文嚼字地探究題目可勾起學生學習的欲望，讓學生在黑暗之中探尋到一點亮光，并循著亮光慢慢走下去。“教是為了不教”，堅持這樣做的好處就是，將來接觸新概念的時候，學生自然而然就會借助這縷亮光尋找通往知識殿堂的康莊大道。

二、形成與同化，相得益彰

新概念有時是對現實生活的直接抽象，有時是對已有知識的同化、進化。從具體情境中直接抽象出數學概念，這種概念教學方法叫概念形成法；由生活到數學，用已有知識類比引入，從“原型”的形成過程中形成新的“模型”，這種概念教學方法叫概念同化法。教學并非“自古華山一條道”，應是“條條大道通羅馬”。兩種路徑都可以化抽象為具體，化陌生為熟悉，在教學中，交叉使用，相得益彰。

例如“一元二次方程”的教學，可以類比“一元一次方程”的教學。將一元一次方程的實際問題，遞升為一元二次方程的實際問題，循序漸進地說明一元二次方程的實際存在，讓學生不會感到知識點來得太突兀。自然而然的教學之態才是尊重客觀規律、適合學生口味的教學常態。

三、變式加拓展，提煉升華

變式教學是數學教學中的常用方法，亦是數學概念教學的重要支點。“橫看成嶺側成峰，遠近高低各不同”，但萬變不離其宗，“山還是那座山，水還是那汪水”。變式就是通過找變中之不變，以不變應萬變。如在“圓的陰影部分面積”這一章，運用基本圖形加變式，可以很好地講清陰影部分面積轉化的問題。

1.呈現基本圖形。

圖1

圖2

母題：在圖1中，兩條平行線中夾著一個三角形，如果不移動三角形上面兩個頂點，只移動下面一個頂點，如圖2，三角形面積有什么變化？

生3：三角形的面積不變。因為在移動過程中，兩條平行線間的距離不變，所以三角形的上底邊上的高不變。

學生回答得很好。帶著這樣的母題背景，教師繼續呈現變式題型。

2.呈現變式1。

變式1：如圖3，半圓的直徑AB=40，C、D是半圓的三等分點，求AC、AD與弧CD圍成的陰影部分的面積。

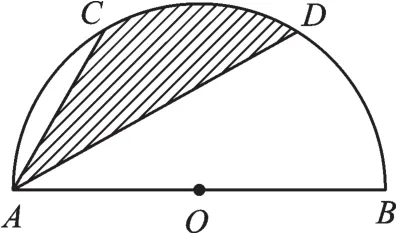
圖3

陰影部分的面積為不規則圖形，直接求很困難。如果有了上面的母題，就知道如果將OC與OD連起來，那么△ACD的面積就轉化為△OCD的面積，再利用扇形面積公式即可。

3.呈現變式2。

變式2：如圖4，AB是圓O的直徑，CD、EF是圓的弦，且AB//CD//EF，AB=10，CD=6，EF=8。求陰影部分的面積。

圖4

圖5

有了變式1的基礎，將A點與B點移到O點，將兩個不規則陰影圖形轉化為規則圖形。再根據6、8、10一組勾股數，將圖形旋轉，使得OF與OD重合，如圖5，△CDE′是直角三角形且CE是直徑。陰影部分就轉化成了半圓。

“變則通”，通過變式讓學生對概念融會貫通。

四、分層應用，各得其所

分層是科學實施有效教學的合理策略。分層教學是根據學生水平的不同，采取不同的教學方式，布置不同的作業，有針對性地對每個學生進行指導的有效教學方法。在平時的學案設計上，筆者針對不同的學生，布置不同的預習題目。在課后作業的布置環節，有“課后作業”與“探究提升”兩塊內容。學有余力的學生兩塊必做，學習費勁的學生必做“課后作業”，選做“探究提升”。在分層作業實施過程中，很多學生慢慢地由選擇“課后作業”變成了既選擇“課后作業”，又選擇“探究提升”。他們都實現了自我價值的提升，各得其所。

概念教學的支點很多，需要我們潛心探尋，積累經驗，從而使其擁有豐富的生命力和持久的推動力。概念教學“活”了，每章中相關知識的延伸與拓展便會理明義現。