金屬低周疲勞過程熱力學熵特征分析及壽命預測模型

朱達榮 徐德軍 劉 濤 汪方斌 儲朱濤

1.安徽建筑大學機械與電氣工程學院，合肥，2306012.安徽建筑大學建筑機械故障診斷與預警技術重點實驗室，合肥，230601

0 引言

疲勞是材料退化的過程，是對其所承受循環載荷的響應[1]。在各類人造結構和自然系統中，疲勞是最主要的失效形式之一[2]。材料的疲勞壽命預測一直是工程界和學術界關注的熱點問題[3]。從能量角度看，疲勞損傷是由內摩擦導致熱耗散的不可逆過程，而熱力學熵[4-5]是系統無序、系統紊亂的度量，能夠描述材料的不可逆退化，可以作為材料疲勞損傷評估指標。

熱力學熵相比于傳統疲勞分析評估方法能夠更好地解釋疲勞損傷過程的物理機制。在利用熱力學熵進行材料疲勞過程分析及壽命預測方面，BRYANT等[6]基于損傷力學與廣義熱力學理論，指出了熵產與材料損傷的不可逆性相關聯，通過試驗發現在改變試驗條件的情況下，材料的最終斷裂熵值仍為定值。AMIRI等[7]開發了一種基于熵流特征量評估臨界疲勞損傷值的方法，確定了不同材料試樣在經受彎曲疲勞作用時的熵流，并評估了臨界損傷值。陳凌等[3,8-9]從熵守恒定律和能量守恒定律出發，推導出了一種新的低周疲勞壽命預測模型。NADERI等[10]通過疲勞斷裂熵(fatigue fracture entropy，FFE)這一熱力學熵特征量闡述了熵產和損傷變量之間的關聯規律，并在此基礎上提出了一種實時疲勞壽命檢測單元。

上述研究表明，熱力學熵相關特征量可進行疲勞壽命預測以及疲勞損傷評估，并且更加貼近疲勞損傷的機理層面，具有廣闊的應用前景。目前國內在基于熱力學熵的構件疲勞損傷評估方面研究較少，熵產率、累積熵產等熱力學熵特征與疲勞損傷的關聯特性尚未明確。本文選取Q235鋼試樣開展不同加載條件(加載幅值、加載頻率)下的低周疲勞試驗，利用熵產率、累積熵產、疲勞斷裂熵等熱力學熵特征量的變化特征描述低周疲勞損傷過程，并評估低周疲勞損傷程度，基于熱力學熵相關特征量建立了一種新的壽命預測模型。

1 理論基礎

疲勞是能量耗散的不可逆過程，由Clausius-Duhem不等式[11-14]可知，在產生內摩擦的固體材料中，所有變形都會導致正熵產值，表達式如下：

(1)

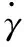
式(1)描述了熵產過程，它由塑性變形引起的塑性應變能耗散：

式中，f為試驗頻率；Δwp為塑性應變能。

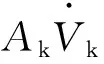
(2)

因此式(1)可簡化為

(3)

在以塑性應變為主的金屬低周疲勞過程中，僅考慮式(3)第一項即可。其熵產表達式可表述為

(4)

即

(5)

其中，Δwp可根據Morrow[18]的理論，由以下循環塑性能耗公式確定[16,19-20]：

(6)

式中，σ′f為疲勞強度系數；ε′f為疲勞延性系數；b為疲勞強度指數；c為疲勞延性指數；Nf為疲勞失效循環周次。

對式(5)從起始時刻t=0到斷裂時刻t=tf進行積分，可得到總熵增計算公式：

(7)

利用試驗采集的試樣標距內最大溫度數據，通過式(5)和式(7)可以計算低周疲勞過程的熱力學熵產率及累積熵產，為基于熱力學熵的低周疲勞損傷評估以及疲勞壽命預測模型的建立提供了理論基礎。

2 熱像特征采集與數據分析

2.1 材料及試樣

試驗材料為Q235板材試樣，尺寸如圖1所示，經X射線熒光光譜分析，得到材料所含元素質量分數如表1所示。試樣由激光切割加工，并沿軸向打磨拋光，為提高試樣表面發射率，試驗前將待測試樣表面均勻噴涂一層黑漆。

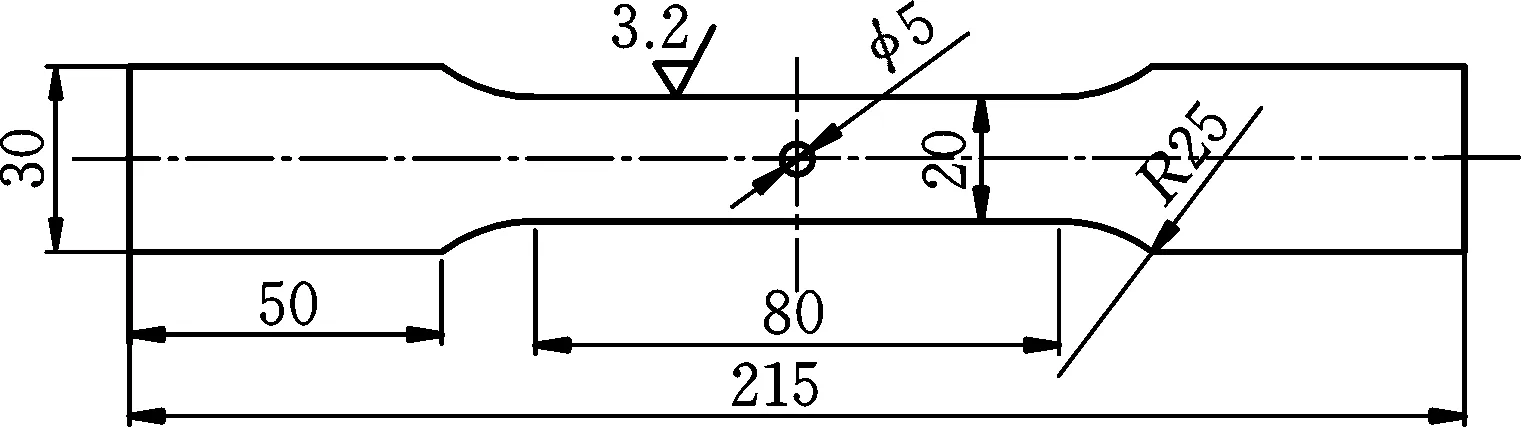
圖1 Q235板試樣(mm)Fig.1 Sample of Q235 plate (mm)

%

進行疲勞試驗前，對Q235鋼試樣進行靜態拉伸試驗，試驗結果表明，材料的抗拉強度為415 MPa，條件屈服極限為300 MPa。圖2所示為Q235鋼試樣在拉伸載荷(以12.5 kN為例)作用下的應力、應變分布。由圖2可見，試樣所受的最大等效應力值為252.7 MPa，最大真實應變為0.129 3%，符合低周疲勞試驗條件。

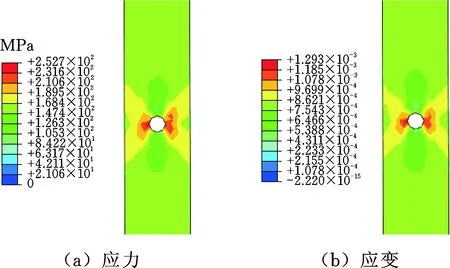
圖2 Q235試樣應力場與應變場云圖Figure.2 Q235 samples stress and strain field cloud map

2.2 紅外熱像特征采集

圖3所示為紅外熱像采集系統。本試驗主要研究承受軸向循環載荷的Q235材料試樣疲勞行為，使用電液伺服疲勞試驗機(中機試驗SDS-200)開展疲勞試驗。為避免試驗場所存在的自然光直射，試驗全過程在室內進行。試驗環境空氣介質無強對流現象，相對穩定，環境溫度為常溫25 ℃。

圖3 紅外熱像采集系統Fig.3 Infrared thermal image acquisition system

如圖4所示，使用FLUKE Ti200紅外熱像儀對試驗過程中試樣表面溫度進行實時監控，熱像儀分辨率為640像素×480像素,熱敏度不超過0.05 ℃。溫度數據以紅外熱像圖的形式保存。采集到的紅外熱像圖使用SmartView軟件分析處理，提取試樣標距內最高溫度值(相當于裂紋尖端溫度)，采集該溫度值作為疲勞過程溫度演化數據。表2為Q235試樣低周疲勞試驗加載條件。

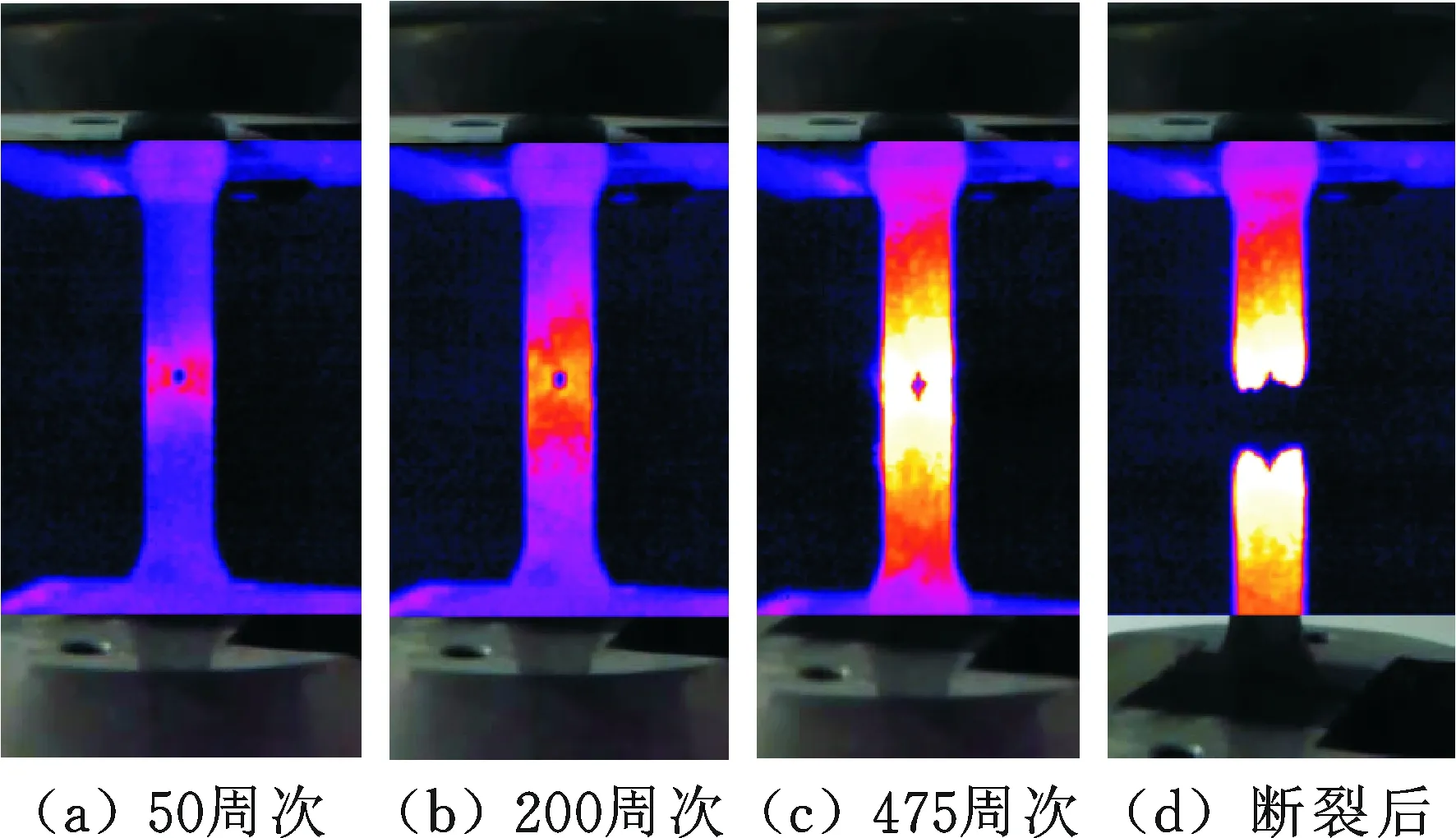
圖4 Q235鋼試樣低周疲勞試驗過程表面溫度Fig.4 Surface temperatures of Q235 samples low-cycle fatigue test

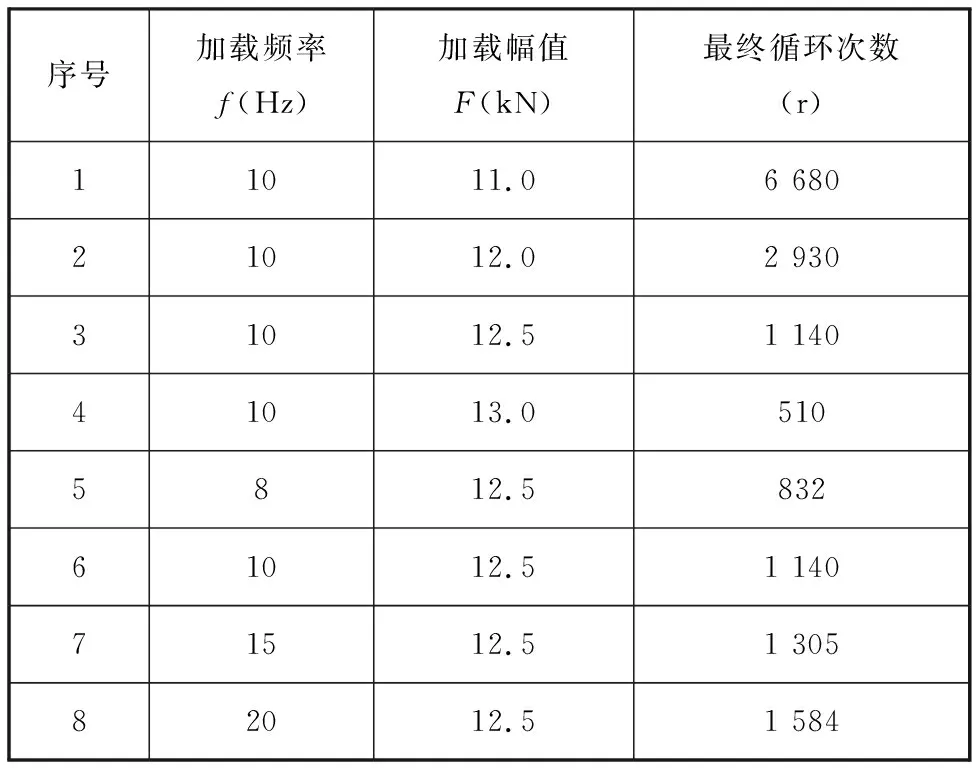
序號加載頻率f(Hz)加載幅值F(kN)最終循環次數(r)11011.06 68021012.02 93031012.51 14041013.05105812.583261012.51 14071512.51 30582012.51 584

2.3 紅外熱像特征數據分析

圖5、圖6所示分別為不同加載幅值和頻率下的Q235試樣低周疲勞過程溫度演化曲線。圖中可見低周疲勞試驗全過程的溫度演化分為3個階段。第一階段，試樣表面溫度從環境溫度快速上升，這一階段試樣受到循環載荷影響，內部發生位錯運動，表面產生侵入擠出現象，試樣內部產能無法快速傳遞到外界，導致表面溫度升高。第二階段，試樣表面溫度相對平穩，試樣內部產能與外界能量交換處于相對平衡狀態。第三階段，試樣表面溫度迅速上升，產生宏觀裂紋及大塑性變形最終試樣發生斷裂。

圖5 不同加載幅值下的溫度演變曲線Fig.5 Temperature evolution curve under different loading amplitudes

由圖5可知，循環載荷幅值越大，第一階段試樣初始溫升速度越快，第二階段的溫度越高，并且試樣最終的斷裂溫度越高。

由圖6可知，對于不同加載頻率，其頻率越低，第一階段溫升斜率越大，且第二階段的溫度相對較高，試樣斷裂時其表面溫度無顯著差異。

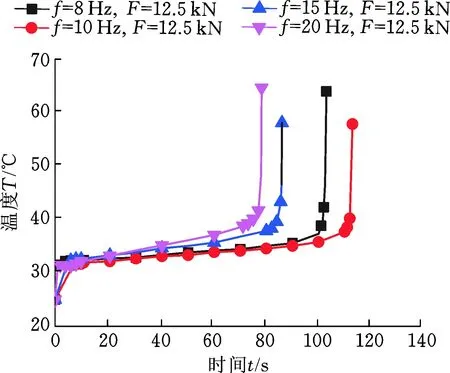
圖6 不同加載頻率下的溫度演變曲線Fig.6 Temperature evolution curves under different loading frequencies

3 熱力學熵特征分析

3.1 不同加載條件下的熵產速率

圖7、圖8所示分別為不同加載幅值與頻率下的Q235試樣低周疲勞過程熵產率曲線。圖中可見，在不同載荷幅值和加載頻率下，熵產率值基本為定值，波動較小。在最初加載與最終斷裂階段，試樣表面溫度升高導致熵產率值發生小幅度下降。當試樣內部產熱功率和熱耗散率基本穩定時，熵產率也相對穩定，該階段占據試樣的大部分疲勞壽命。

圖7 不同加載幅值下的熵產率曲線Fig.7 Entropy generation rate curves under different loading amplitudes

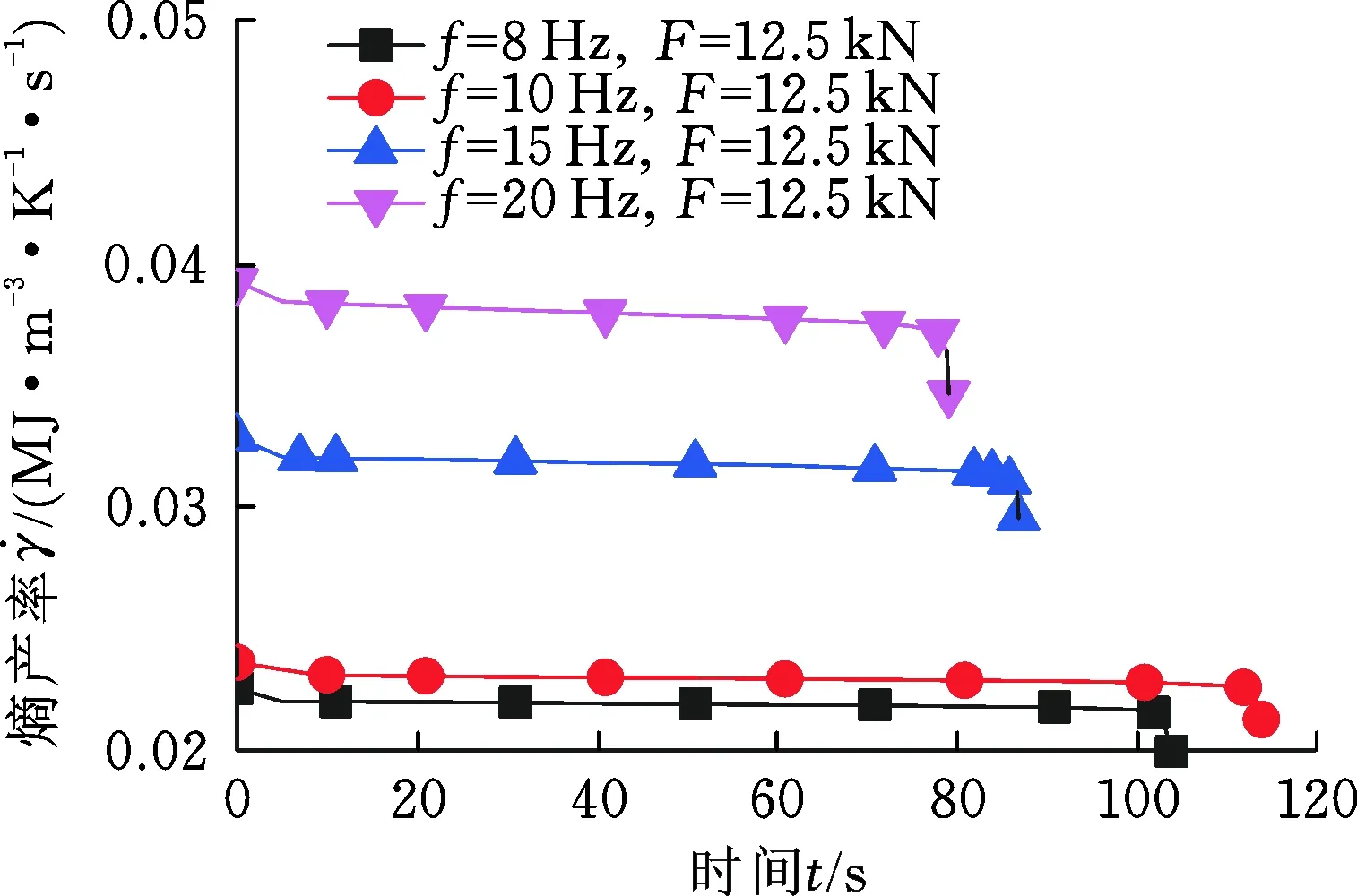
圖8 不同加載頻率下的熵產率曲線Fig.8 Entropy generation rate curves under different loading frequencies

熵產率作為材料熱力學維度的損傷速率，由圖7可知，較小的加載幅值使試樣在循環載荷作用下產生的能量釋放較少，表面溫升較低，因此，加載幅值較小時熵產率相對較低。加載幅值越高，單位時間產生的塑性應變能越多，熵產率越大。

如圖8所示，載荷頻率降低，材料損傷進程減緩，釋放出較低的能量，表面溫升較低，因此，加載頻率越低熵產率越低。

3.2 低周疲勞過程累積熵的變化趨勢

疲勞過程的累積熵產可用熵產率曲線與時間橫軸圍成的面積表示，即通過熵產率對時間進行積分獲取。圖9和圖10所示分別為不同加載幅值和頻率下的熵產累積變化曲線。圖中可見，疲勞過程的熱力學熵產累積是一個準線性累加過程。試樣最終斷裂時，累積熵產值達到最大即疲勞斷裂熵。

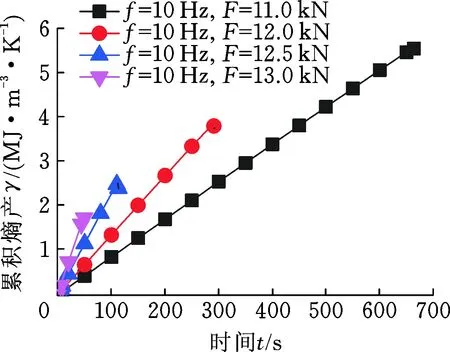
圖9 不同加載幅值下的熵累積曲線Fig.9 Entropy accumulation curves under different loading amplitudes

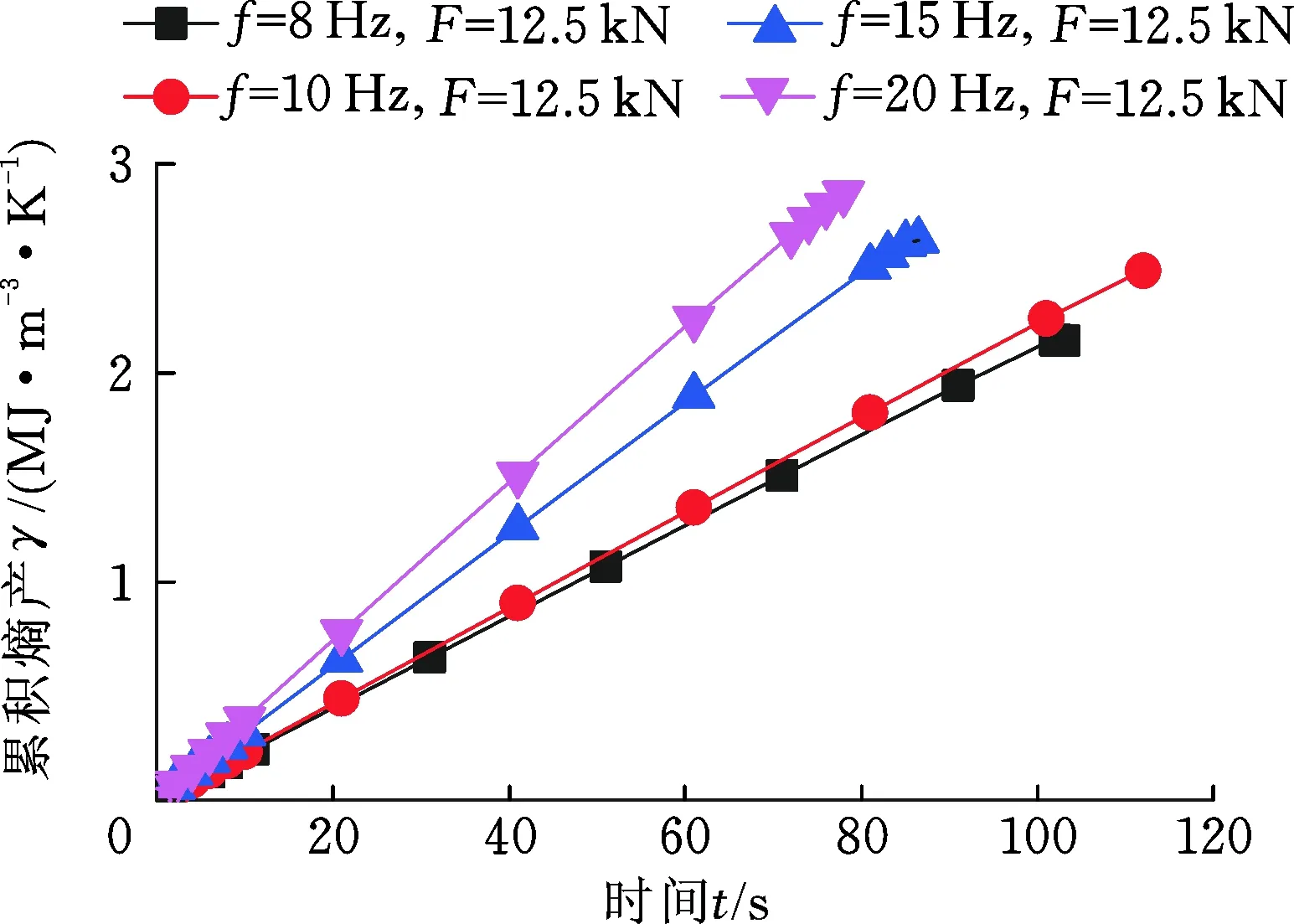
圖10 不同加載頻率下的熵累積曲線Fig.10 Entropy accumulation curves under different loading frequencies

由圖9可知，加載載荷越大，累積熵產曲線斜率越大，越快達到累積熵產頂點，即在不同加載載荷下，加載幅值越大，試樣斷裂越快，熵產累積速率越快，熵產累積時間越短，其最終疲勞斷裂熵值越小。

由圖10可知，加載頻率越高，熵累積速率越快，即累積熵產曲線越陡，越快達到斷裂熵值。與此同時，同一加載幅值不同加載頻率下，試樣的疲勞斷裂熵值相對一致，本試驗中，在加載幅值為12.5 kN條件下，不同加載頻率的疲勞斷裂熵值約為2.579 MJ/(m3·K)。

3.3 低周疲勞的疲勞斷裂熵

圖11所示為Q235試樣在相同頻率不同載荷下的疲勞斷裂熵值。由圖可見，低周疲勞過程Q235鋼試樣的疲勞斷裂熵隨加載幅值的增大而減小。

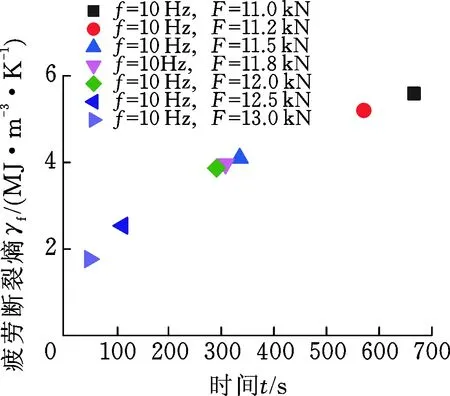
圖11 Q235試樣低周疲勞試驗同頻率下的疲勞斷裂熵Fig.11 FFE of Q235 low cycle fatigue testsunder the same frequency

圖12所示為兩組載荷相同、加載頻率不同的疲勞斷裂熵值散點圖。由圖可見，Q235鋼試樣的疲勞斷裂熵與加載頻率無明顯關系，僅與加載載荷相關。本試驗中，加載幅值為12.5 kN時和11.0 kN時，不同加載頻率下的疲勞斷裂熵值約為2.579 MJ/(m3·K)和5.656 7 MJ/(m3·K)。

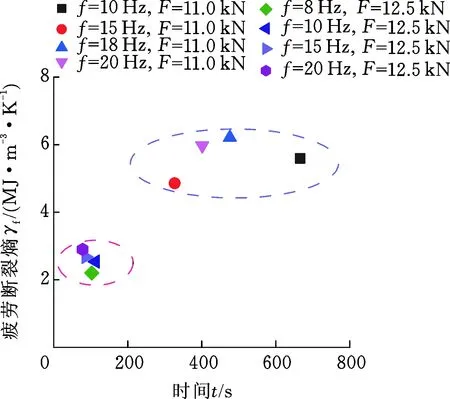
圖12 Q235試樣低周疲勞試驗同載荷下的疲勞斷裂熵Fig.12 FFE of Q235 low cycle fatigue tests under the same load

3.4 基于熱力學熵的疲勞壽命預測模型

在分析疲勞斷裂熵與加載幅值的關系的基礎上，利用指數函數建立載荷與斷裂熵之間的函數模型：

γf=AeBF

(8)

其中，A、B為模型參數。表3為函數模型回歸試驗數據及擬合參數。

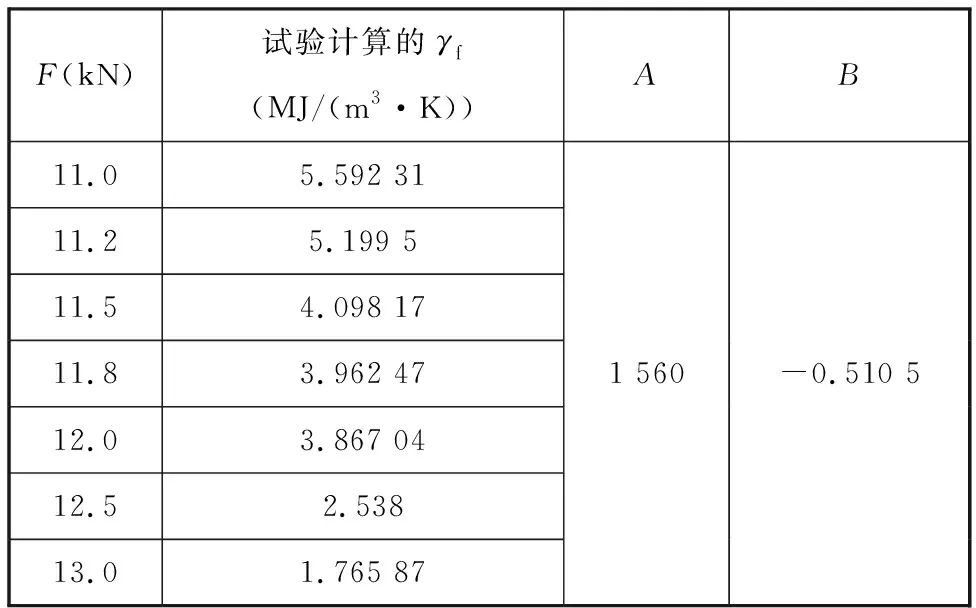
表3 擬合模型參數表

圖13所示為載荷幅值與疲勞斷裂熵之間的擬合曲線。圖14為利用試驗數據對模型進行驗證的誤差分析圖，模型驗證誤差小于18%。

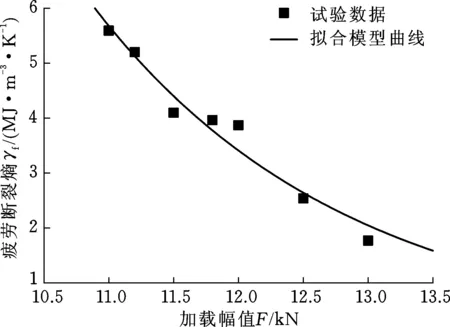
圖13 載荷幅值與疲勞斷裂熵擬合曲線Fig.13 Fitting curve of load amplitude and fatigue fracture entropy

圖14 模型驗證誤差分析曲線Fig.14 Error analysis of model verification

前述研究表明，低周疲勞過程疲勞斷裂熵可根據相應的加載幅值求得。在疲勞損傷過程中，提取材料表面溫度信息后就可以計算實時熵值，將其與疲勞斷裂熵對比可進一步評估材料損傷狀態。將累積熵產與循環周次歸一化，歸一化后累積熵產與循環周次近似為線性關系，如圖15及下式所示：

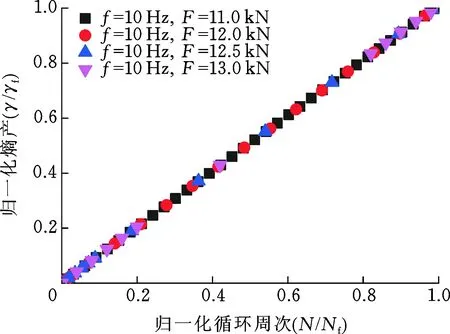
圖15 歸一化熵產與歸一化循環周次Fig.15 Normalized entropy production and normalized cycle times

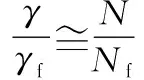
(9)

對式(9)進行變形得到：

(10)

將式(8)代入式(10):

(11)

由式(9)和式(11)可見，疲勞損傷過程某一熵產累積值對應于一特定損傷狀態。作為衡量系統不可逆性和組織無序性的特征參數，熵產可用來描述材料內部位錯、滑移等導致的不可逆損傷。

另外選取6組同批次Q235鋼試樣開展低周疲勞試驗，加載幅值均為11.5 kN，加載頻率均為10 Hz，其中，1～4組分別提取試樣在不同循環周次下的表面溫度信息，從而獲取該狀態的熱力學熵特征，對壽命進行預測，用于模型驗證。5、6兩組采集試驗過程中的應力幅值和應變幅值數據，運用經典Manson-Coffin和Basquin模型[9]開展壽命預測對比，結果見表4。

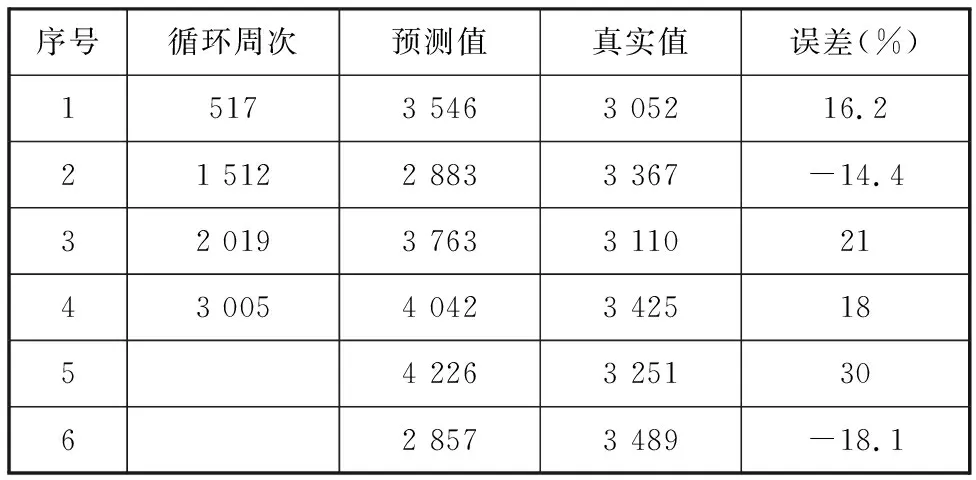
表4 疲勞壽命預測模型驗證結果

表4數據表明，傳統的Manson-Coffin和Basquin模型與本文的壽命預測模型預測誤差均在14%～30%范圍內，本文模型可用于疲勞壽命預測。本文模型可通過提取試樣疲勞過程的各階段特征進行壽命預測，與傳統模型相比更具實時性。

4 結論

(1)本文選取熵產率和累積熵產作為疲勞損傷評估指標，通過研究發現，同一加載幅值下疲勞損傷過程熵產率基本恒定，且熵產率隨著加載幅值及頻率的增大而增大。疲勞損傷過程熱力學熵的累積是一個準線性累加過程，其熵產累積速率隨著加載幅值和頻率的增大而加快，即熵產曲線的斜率越大，越快達到熵產曲線頂點。

(2)選取Q235材料試樣開展不同加載幅值和加載頻率下的低周疲勞試驗。試驗發現，不同加載條件下疲勞斷裂熵隨加載幅值增大而減小，與加載頻率無明顯關系。

(3)明確了疲勞斷裂熵與加載幅值之間的函數關系，并通過分析歸一化的疲勞累積熵與循環周次關聯特性，建立了疲勞壽命預測模型，為金屬構件疲勞壽命預測提供了新思路。

(4)后續將開展熱力學熵特征量、磁特征量等多特征量融合的疲勞損傷評估，以降低評估不確定性，提高評估精度。這也是開展疲勞損傷研究的重點和難點。