橡膠襯套高階分數導數動力學模型的研究*

高 琦，馮金芝，鄭松林，林 陽

（1.上海理工大學機械工程學院，上海 200093； 2.上海匯眾汽車制造有限公司，上海 200122）

前言

橡膠襯套的動態性能影響懸架的動力學特性，它具有較強的非線性黏彈力學特性，受加載幅值、加載頻率和工作周期等因素的影響［1］。襯套模型的精度是懸架及整車動力學仿真精度的關鍵影響因素之一，目前整車及子系統模型動態仿真精度不足很大原因是襯套模型精度不夠造成的［2］。因此，建立準確描述襯套動態特性的動力學模型，對提高整車仿真精度、準確預測懸架動態K＆C特性對整車操穩性和平順性的影響具有重要意義。

目前為止，國內外研究人員提出了多種橡膠元件的動力學模型，為克服Kelvin-Voigt模型、三參數Maxwell模型和由多個Maxwell單元并聯得到的廣義橡膠襯套動力學模型的不足，近年來提出的分數導數模型因能反映加載歷程對橡膠材料動態特性的影響而日益受到關注［3-7］，這類模型均為最高階次不大于1的低階分數導數模型，研究人員發現，最高階次大于1的高階分數導數模型更接近于描述橡膠材料的物理本質，對黏彈性力學特性的描述更加精確［8-9］，但相關研究文獻相對較少，因此，本文中嘗試用高階分數導數模型描述橡膠襯套的黏彈性力學特性，建立橡膠襯套黏彈性高階分數導數動力學模型。

以某車用懸架擺臂橡膠襯套為研究載體，進行動態加載試驗，分析其軸向頻率相關性和振幅相關性；建立基于彈性單元、摩擦單元和高階分數導數黏彈性單元并聯的橡膠襯套力學模型，提出一種基于動態鄰居廣義學習策略粒子群優化（dynamic neighbor and generalized learning particle swarm optimization，DNGL-PSO）算法的高階分數導數黏彈性單元參數識別方法，并結合試驗結果對模型參數進行識別；進一步，為提高模型整體的預測精度和適用性，將黏彈性單元的分數導數系數擬合為加載振幅的函數。通過與試驗結果對比，驗證所建立的模型能夠精確地描述懸架襯套軸向的動態特性。

1 橡膠襯套動態加載試驗

基于MTS831襯套試驗臺進行了某車用懸架擺臂橡膠襯套軸向動態加載試驗，激勵為振幅和頻率一定的正弦信號，試驗裝置與夾具的安裝方式如圖1所示。

圖1 橡膠襯套軸向動態加載試驗

試驗對象為軸對稱圓柱形橡膠襯套，考慮該襯套在工作過程變形受到約束，這里僅通過動態加載試驗研究其在線彈性變形范圍內的動態特性。通過分析該懸架襯套的工作特性，進行了頻率范圍為1～40 Hz、振幅為0.1～2 mm的動態加載試驗，得到的橡膠襯套的動剛度和阻尼系數隨振幅和加載頻率的變化規律如圖2和圖3所示。

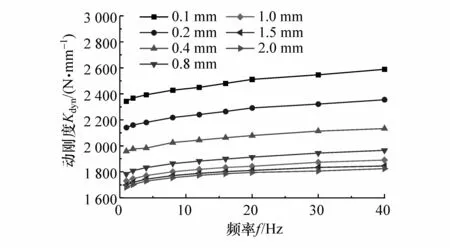
圖2 不同加載幅值下襯套動剛度隨頻率的變化

圖3 不同加載幅值下襯套阻尼系數隨頻率的變化

由圖2和圖3可以看出：1～40 Hz頻率范圍內，當振幅一定時，橡膠襯套的動態剛度和阻尼系數都隨著頻率的增加而增大；隨著振幅的增加，橡膠襯套的動剛度顯著下降，阻尼系數隨著振幅的增加先增大至峰值再呈現出減小的趨勢。

2 橡膠襯套動力學建模

所建立的襯套動力學模型由彈性單元、摩擦單元和黏彈性單元并聯組成，如圖4所示。

圖4中Fe，Ff，Fv和F分別為彈性單元、摩擦單元、黏彈性單元和襯套總模型的響應力，N。

2.1 彈性單元和摩擦單元

襯套軸向彈性特性在線變形范圍內符合胡克定律［10］：

式中：Fe為彈性力，N；x為襯套變形量，mm；Ke為靜態彈性剛度，N·mm-1。在振幅為 x0的正弦激勵下，彈性力的幅值Fe0為Kex0，且無能量損耗。

圖4 橡膠襯套動力學模型組成示意圖

摩擦單元中摩擦力與位移的關系為［10］

式中：Ff為摩擦力，N；x為加載位移，mm；Ffmax為最大摩擦力，N；x2為Ff從0開始，增加至 Ffmax／2時的位移，mm；（xs，Ffs）為摩擦力隨位移變化曲線上的狀態參考點，此處取（0，0）；sign（x·）為位移的變化方向，位移增加時為正，反之為負。在振幅為x0的正弦激勵下，摩擦力的幅值和損耗的能量分別為

式中：Ff0為摩擦力的幅值，N；Ef為一個周期損耗的能量，N·mm；a0＝Ff／Ffmax。

2.2 黏彈性單元

基于傳統黏彈力模型，Gemant等［11］學者提出了分數導數模型，因能反映加載歷程對黏彈性材料動態特性的影響，得到廣泛應用。最常見的分數導數Kelvin-Voigt模型和Maxwell模型，進一步提出的分數導數Zener模型以及在此基礎上提出的包含兩個不同分數階的分數導數模型，均為最高階次不大于1的低階分數導數模型，在模擬橡膠材料隨頻率的變化趨勢中的損耗模量存在一定誤差［6］。高階（模型參數取不同值時最高階次大于1）分數導數模型對黏彈性力學特性的描述更加精確［8］，因此本文中通過將分數導數Kelvin-Voigt模型和Maxwell模型并聯，建立高階分數導數模型描述橡膠材料的黏彈特性，如圖5所示。

圖5 高階分數導數黏彈力模型示意圖

圖5 中，k1和 c1分別為分數階Kelvin-Voigt模型中彈簧的彈性模量和黏壺的黏性系數，k2和c2分別為分數階Maxwell模型中彈簧的彈性模量和黏壺的黏性系數。k1和k2反映了材料的彈性，c1和c2反映了材料的黏性。

根據圖5，黏彈力與位移的關系為

式中：λ1＝k1／c1；λ2＝k2／c2；Fv（t）為黏彈性力，N；x（t）為加載位移，mm；α，β和 γ為分數導數階數，取值范圍均為（0，1），其中最高階數為 α+γ（最大值為2）。對式（5）進行傅里葉變換：

則該分數導數黏彈力單元確定的復剛度為

式中：K*v（ω）為黏彈力單元的復剛度，N·mm-1；將

進一步推導出，在振幅為x0的正弦激勵中，響應力實部和虛部的幅值Fv0Re和Fv0Im分別為

一個加載循環中的能量損耗為

式中Ev為一個加載周期的能量損耗，N·mm。

2.3 橡膠襯套動力學模型

將彈性單元、摩擦單元與黏彈性單元并聯，得到襯套動力學模型響應力和加載位移的關系為

式中：F（x）為襯套模型的響應力，N；Fe（x），Ff（x）和Fv（x）分別為彈性單元、摩擦單元和黏彈性單元的響應力，N；x為加載位移，mm。

襯套模型響應力振幅為式中：Fe0和Ff0分別為彈性單元和摩擦單元響應力振幅，N；Fv0Re和Fv0Im分別為黏彈性單元響應力實部和虛部振幅，N。

一個加載循環中，襯套模型的能量損耗為

式中：Ef和Ev分別為一個加載循環中摩擦單元和黏彈性單元的能量損耗，N·mm。

振幅為x0的正弦加載工況下，襯套的動剛度和阻尼系數可通過式（15）和式（16）計算得到：

式中：Kdyn為襯套模型的動剛度，N·mm-1；D為襯套模型的阻尼系數，（N·s）·mm-1。

3 橡膠襯套力學模型參數識別

3.1 彈性單元和摩擦單元參數的識別

選取頻率為1 Hz、振幅為2 mm正弦加載試驗工況作為兩個單元參數的識別工況，該工況下響應力F與位移x的遲滯環曲線如圖6所示。

圖6 低頻加載工況下位移與力的關系曲線

根據圖6，位移接近極限位置處曲線的斜率可近似表示該襯套彈性單元的靜態彈性剛度Ke。延長接近極限位置的上、下兩條切線，摩擦力模型中最大摩擦力Ffmax的值即為兩條切線間的垂直距離的1／2。取曲線的最大斜率的值Kmax，由式（17）可求得摩擦力單元中的x［10］。

彈性單元和摩擦單元參數識別結果見表1。

表1 彈性單元和摩擦單元參數識別結果

3.2 黏彈性單元參數的識別

黏彈性單元參數 k1，c1，k2，c2，α，β和 γ7個參數通過小振幅激勵下襯套動態特性獲得［10］，為充分體現襯套在不同頻率下的非線性黏彈特性，選取振幅為 0.1 mm、頻率分別為 1，2，4，8，12，16，20，30和40 Hz的9個正弦加載試驗工況進行7個參數的識別。

黏彈性單元參數識別實質上為最優參數估計問題，為使識別結果盡可能接近試驗數據，設置襯套動力學模型計算的襯套動態參數值與試驗值的誤差最小的優化函數來實現。因此，建立基于動剛度和阻尼系數誤差優化的目標函數：

為保證黏彈性單元參數識別的準確性，提高橡膠襯套模型的整體預測精度，參數識別過程中，需確保各頻率工況下模型計算得到的與試驗值均不能有較大誤差。一般認為模型的計算精度在90%以上，即可滿足工程應用需要，因此，建立約束條件：

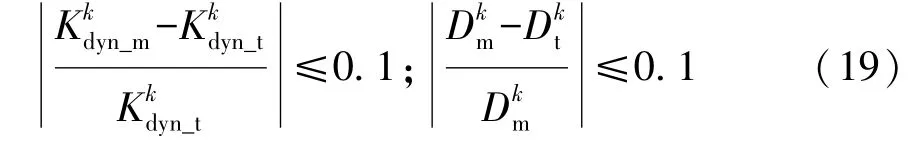
由于高階分數導數黏彈性單元為復雜的非線性模型，且需要識別的參數個數較多，粒子群優化（particle swarm optimization，PSO）算法，作為一種非解析尋優算法，具有大范圍收斂性（不需要較好的近似值作為搜索的起點，有效避免對初值的敏感性）、高效并行、魯棒性和通用性強等優點，對非線性系統參數識別效果較好，且能夠實現多參數識別［12-13］，因此，把PSO算法引入到高階分數導數黏彈力模型參數識別中。為提高算法性能，避免陷入局部極值點，提出一種基于動態鄰居廣義學習策略的粒子群優化（dynamic neighbor and generalized learning particle swarm optimization，DNGL-PSO）算法的高階分數導數黏彈性單元參數識別方法。通過在PSO算法中引入鄰居動態組建策略和廣義學習策略，來降低參數識別過程中算法陷入局部最優解的可能性，使算法有較大的概率向全局最優解收斂，從而提高黏彈性單元參數的識別精度。

在DNGL-PSO算法運行過程中每一迭代時刻，各粒子根據自身適應度函數值動態地組建鄰居，選擇與其歐氏距離較近的粒子作為鄰居，鄰居個數為群規模的 1／4～1／3［14］。同時，引入一種廣義學習策略，使各粒子“個體學習”部分的學習樣本為其所有鄰居（包含其自身歷史最優位置），保證粒子的每一維學習對象在當前迭代時刻為最優。粒子i第d維的學習樣本pdbn_i的選取規則為

式中：pi和Fit（pi）分別為粒子 i的歷史最優位置及其所對應的適應度值；n為種群規模；Ri為粒子i的鄰居構成的集合。

粒子i的速度和位置更新公式為

式中：t為當前迭代次數；v-i（t）為粒子i在第t代的速度；x-i（t）粒子i在第t代的位置；ω為粒子的慣性權重；ε1和ε2為粒子的學習因子；r1和r2為相互獨立在［0，1］均勻分布的隨機數；pg（t）為整個粒子群迄今為止搜索到的最優位置；pbn_i（t）為“個體學習”部分粒子i每一維的學習樣本。其中，ω為線性遞減。

以式（18）所示目標函數為適應度函數Fit（t），采用DNGL-PSO算法對黏彈性單元參數識別，經過多次調試，最終算法參數設置如下：取種群規模n為48，每個粒子的鄰居個數為16；慣性權重ω為0.9～0.4線性遞減；學習因子 ε1和 ε2均為2；r1和 r2為在［0，1］均勻分布的隨機數；粒子維數d為7，位置向量xi＝（k1，c1，k2，c2，α，β，γ），考慮所建高階分數導數單元的特點和參數識別結果的準確性，設置粒子各維搜索空間下限xmin＝（0，0，0，0，0，0，0），上限xmax＝（103，103，103，103，1，1，1）；最大迭代次數 Gmax取200。

基于DNGL-PSO的高階分數導數黏彈性單元參數識別流程如圖7所示，識別結果如表2所示。

表2 黏彈性單元參數識別結果

4 橡膠襯套動力學模型驗證及修正

4.1 橡膠襯套動力學模型驗證

模型參數識別完成后，基于襯套動力學模型進行了不同頻率和振幅的正弦激勵動態仿真計算，結果如圖8和圖9所示，當前模型預測的襯套動剛度和阻尼系數與頻率和振幅的關系均與試驗結果（圖2和圖3）一致。由于摩擦單元的能量損耗不受頻率影響，既使在激勵頻率接近于零時，由模型計算出的襯套能量損耗仍呈現一定的值。因此，該模型能夠較為準確地反映橡膠襯套軸向動態特性分布特征。

圖7 基于DNGL-PSO的黏彈性單元參數識別流程圖

圖8 襯套動剛度預測結果

預測值與試驗結果的對比如圖10和圖11所示，基于小振幅試驗工況識別出的黏彈性單元參數，使所建立的高階分數導數黏彈性襯套模型能夠在較寬頻率范圍內精確地預測襯套的軸向動態特性。但對于大振幅加載試驗工況，預測精度有所下降。

4.2 橡膠襯套動力學模型修正與驗證

試驗和研究表明，除頻率外，振幅對襯套的黏彈特性也有一定影響［2］。為提高模型對大振幅試驗工況的預測精度，對當前模型進行修正。分數導數黏彈性模型中，分數導數階數是描述黏性強弱的物理參數，對于特定材料，階數是固定的［15］。因此，進一步地，將黏彈性單元的分數導數系數k1，c1，k2和c2設為與加載振幅相關，對當前模型進行修正。

令小振幅工況下識別出的分數導數階數α，β和γ保持不變，采用DNGL-PSO算法，根據振幅為0.1，0.8和2 mm的不同加載頻率（每個振幅下均包含1，2，4，8，12，16，20，30和 40 Hz 9個頻率工況）的試驗結果對單元中的k1，c1，k2和c2重新進行識別，并使用二次多項式擬合各參數與振幅x0的關系：

基于新修正的高階分數導數黏彈性并聯襯套動力學模型，進行正弦激勵動態仿真計算，與試驗結果進行對比，如圖12和圖13所示。可見最終建立的黏彈性高階分數導數并聯動力學模型在各種試驗工況下均具有較高的預測精度。

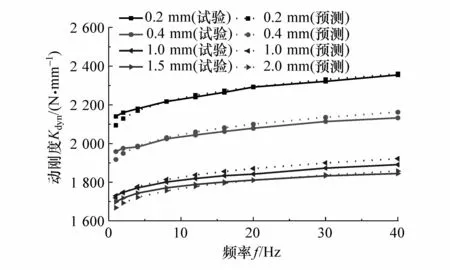
圖12 襯套動剛度模型預測值與試驗值對比

圖13 襯套阻尼系數模型預測值與試驗值對比

在振幅為0.1～2 mm之間，頻率在1～40 Hz之間，分別對初期模型、最終模型預測結果與試驗結果進行統計，得到兩個模型對各加載振幅工況的襯套動剛度和阻尼系數最大預測誤差的平均值和最大值，如表3所示。

由表3可看出，最終模型能夠準確描述預測工況內橡膠襯套軸向的動態特性，其中，動剛度的平均誤差和最大誤差分別為1.99%和2.82%，阻尼系數的平均誤差和最大誤差分別為5.03%和5.76%。

表3 初期模型和最終模型對各加載振幅下最大預測誤差的對比結果 %

文獻［3］中包含低階分數導數黏彈性單元的襯套模型，對阻尼系數預測最大誤差為10.43%，本文中所建模型顯著降低了模型在預測工況內的波動，說明高階分數導數黏彈性單元能夠有效減小模擬橡膠材料隨頻率變化的阻尼特性的誤差。文獻［16］中基于多個黏彈性單元疊加的襯套模型，對動剛度和阻尼系數最大預測誤差分別為6%和8%，精度較高，但對襯套材料物理本質的描述不夠準確，本文中所建襯套模型具有很高的整體預測精度和適用性，能更加接近地描述襯套材料的物理本質。

5 結論

（1）以某車用擺臂橡膠襯套為載體，通過動態加載試驗對其軸向頻率相關性和振幅相關性進行了研究，建立了基于彈性單元、摩擦單元和高階分數導數黏彈性單元并聯的動態力學模型；

（2）通過在粒子群算法中引入鄰居動態組建策略和廣義學習策略，提出了一種基于DNGL-PSO算法的高階分數導數黏彈性單元參數識別方法；

（3）采用小振幅加載試驗結果對黏彈性單元的分數導數階數進行了識別，將黏彈性單元的分數導數系數擬合為加載振幅函數，并基于小、中和大3種振幅加載試驗工況進行了識別；

（4）通過模型計算結果與試驗結果對比，采用該方法建立的高階分數導數襯套模型，具有很高的整體預測精度和適用性，能夠準確描述懸架工作狀態下的襯套軸向的頻率相關性和振幅相關性，以期為復雜工況下準確預測懸架動態K＆C特性對整車操穩性和平順性的影響奠定基礎。