一類高斯混合噪聲干擾的系統拆分與濾波方法設計
寧子健 楊艷萍 馮肖亮


摘? 要:文章針對這樣一類系統:狀態方程與觀測方程中含有均值為零的高斯噪聲且含非零均值的高斯噪聲,提出了一種基于系統噪聲拆分的濾波算法。首先將狀態方程與觀測方程分別拆成兩個僅含有一個噪聲的方程;然后,對兩個方程分別進行濾波;最后,進行融合。仿真結果表明相比直接使用卡爾曼濾波方法,系統噪聲拆分方法提高了濾波的估計精度。
關鍵詞:零均值的高斯噪聲;卡爾曼濾波;系統噪聲拆分
中圖分類號:TN713? ? ? ? 文獻標志碼:A 文章編號:2095-2945(2019)23-0104-02
Absrtact: In this paper, a filtering algorithm based on system noise split is proposed for such a class of systems: the equation of state and the observation equation contain Gaussian noise with zero mean and non-zero mean. First, the state equation and the observation equation are divided into two equations with only one noise; then, the two equations are filtered respectively; finally, the fusion is carried out. The simulation results show that compared with the Kalman filter method, the system noise resolution method improves the estimation accuracy of the filter.
Keywords: zero mean Gaussian noise; Kalman filter; system noise resolution
1 概述
卡爾曼濾波是最小均方估計意義下的一種迭代遞歸算法,求出的線性系統中的估計值是最優的,使得卡爾曼濾波的使用越來越廣泛[1-3]。但是它的噪聲要求必須是均值為零的高斯噪聲。但是當狀態方程與觀測方程中同時含有均值為零的高斯噪聲與非零均值的高斯噪聲時,它可能并不是最優的,因此本文提出了一種基于系統噪聲拆分的方法。
2 系統描述
考慮如下系統的狀態方程:
上式中,x(k)為k時刻的系統狀態,y(k)為k時刻的系統觀測,F(k,k-1)為狀態轉移矩陣,H(k)為觀測方程轉移矩陣。
3 基于系統噪聲拆分的濾波器[4]
狀態方程與觀測方程分別含有均值為零的高斯噪聲和非零均值的高斯噪聲時,將系統中狀態方程拆分成含有高斯噪聲的子系統和均值不為零的高斯噪聲的子系統,同樣,將系統中觀測方程拆分成含有高斯噪聲的子系統和均值不為零的高斯噪聲子系統。
5 結論
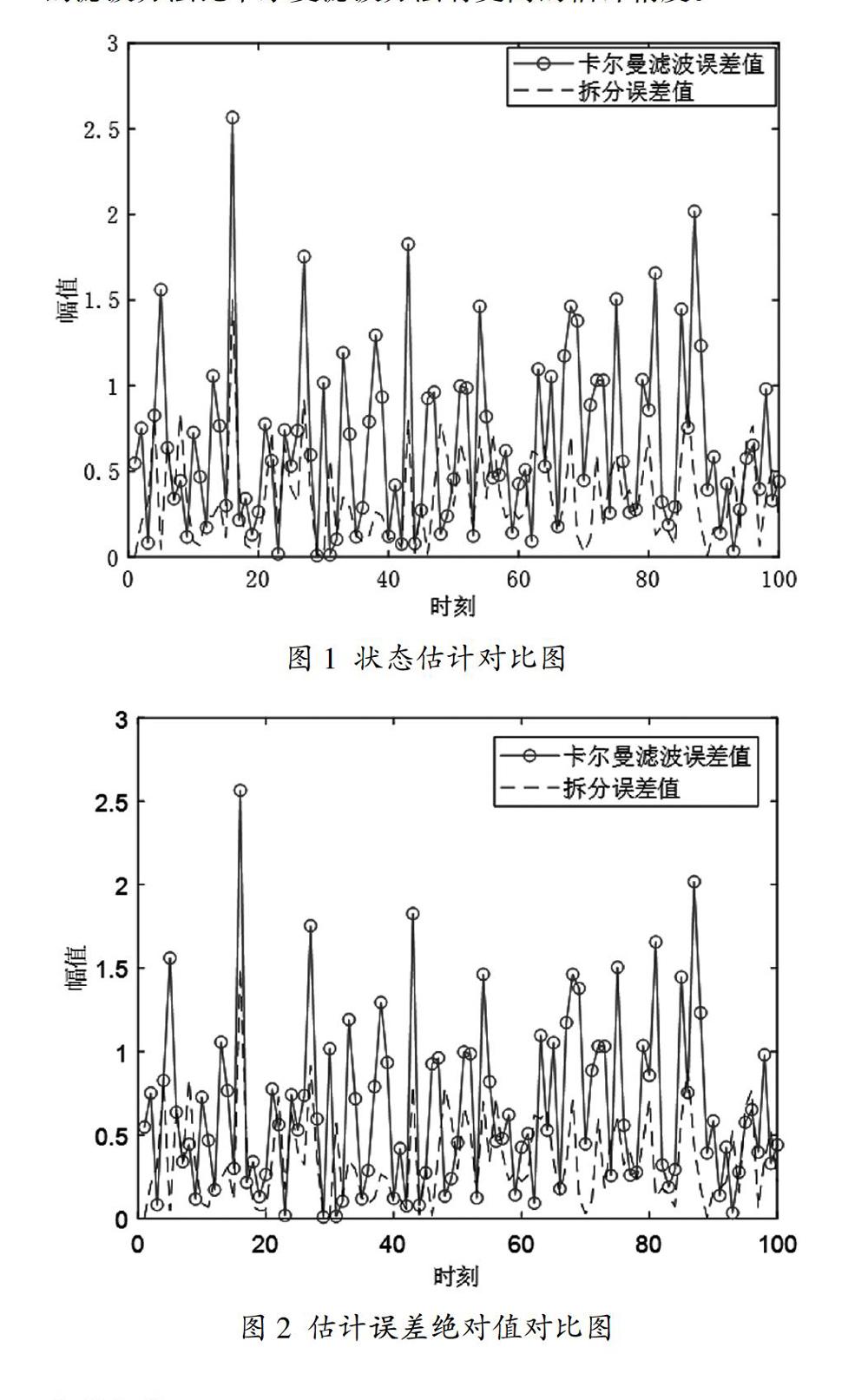
本文對狀態方程與觀測方程中含有均值為零的高斯噪聲與非零均值的高斯噪聲,將狀態方程與觀測方程分別拆成兩個只含有一個噪聲的子系統,組合成兩個子系統,分別進行濾波并融合。仿真結果表明,基于系統噪聲拆分的濾波方法比卡爾曼濾波方法有更高的估計精度。
參考文獻:
[1]Kalman, R. E . A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering, 1960,82(1):35.
[2]彭丁聰.卡爾曼濾波的基本原理及應用[J].軟件導刊,2009,8(11):32-34.
[3]張友民,戴冠中,張洪才.卡爾曼濾波計算方法研究進展[J].控制理論與應用,1995(05):529-538.
[4]宋義軒,馮肖亮.基于觀測分解的一類非線性濾波方法[J].科技創新與應用,2018(05):91-92.

