姿控動力系統連接螺釘振動疲勞仿真分析研究
薛 杰,王 偉,杜大華,隋祿濤
(液體火箭發動機技術重點實驗室,陜西 西安 710100)
0 引言
隨著現代工業的發展,結構在力學環境中出現的振動斷裂問題越來越多,特別是航空航天、化工、兵器及船舶等工程領域,振動環境對結構帶來的影響更為突出。而為了確保產品結構安全、可靠運行,目前往往需要通過隨機振動試驗來考核力學環境下結構的適應性或從中尋找結構的薄弱環節。但是,一方面由于振動試驗工作周期長、試驗設備及保障成本高;另一方面,振動試驗難于定量地給出被試結構在試驗中產生的疲勞損傷,尤其是各種連接件根部的細小位置處。因此,能夠運用仿真技術進行結構振動試驗的模擬并進行振動疲勞損傷的有效估算就顯得格外重要。
自1985年Turan Dirlik發表他的博士論文[1]以來,國外對振動疲勞的研究已從理論逐步走向工程應用,國內學者在這一領域也做了很多工作,其中,文獻[2-9]分別對不同結構在隨機振動環境下進行疲勞損傷的研究,均取得了較好的效果,說明了Dirlik方法的可行性及有效性。本文在該方法的基礎上,通過單階模態響應,對某姿控動力系統在隨機振動試驗中發生疲勞斷裂的連接螺釘進行損傷分析,為結構改進提供一定的參考。
1 振動疲勞壽命估算方法
1.1 材料疲勞性能描述
目前,描述金屬材料疲勞性能的主要方式包括應力壽命(s-N)曲線及應變壽命(ε-N)曲線。其中,s-N曲線通常用于高周疲勞分析,ε-N曲線則用于低周疲勞分析。由于冪函數公式描述材料的疲勞屬性為
sb·N=C
(1)
式中:b,C為材料壽命參數,通過對上式兩邊取對數,可以發現在雙對數坐標下s與N的關系變成一條直線,與一般金屬相應的高周疲勞曲線基本一致。因此,在本文研究的結構高周振動疲勞問題中適合采用式(1)進行分析。
1.2 振動應力應變歷程算法
對于穩態隨機振動過程,通常運用統計的方法對相應結構應力應變歷程進行描述,而在振動疲勞分析中比較成功的描述方法為Dirlik法。
在文獻[1]中,Dirlik法通過對70種不同分布形狀的功率譜函數進行模擬分析,所模擬的功率譜函數的不規則因子γ的變化范圍從0.16~0.99,適用于寬帶及窄帶的情況,最終得到其雨流循環幅值概率密度函數的經驗公式。Dirlik公式由一個指數函數、帶瑞利參數的瑞利函數及標準瑞利函數共同組成[10]
(2)
其中
D3=1-D1-D2
式中:Z為正則化幅值;s為應力幅值;P(s)為應力雨流循環的幅值概率密度函數;m0,m1,m2,m4分別為應力響應功率譜密度函數的零階矩、一階矩、二階矩及四階矩。與部分文獻不同的是,式(2)中采用應力幅值概率密度函數而不是應力范圍概率密度函數,是因為本文采用的s-N曲線中s指的是應力幅值而不是應力范圍,二者為兩倍關系

(3)
式中:mi為功率譜的i階矩;f為頻率;G(f)為應力單邊功率譜。
1.3 疲勞累積損傷理論
疲勞累積損傷目前存在多種理論,其中Palmgren-Miner線性累積損傷理論是最經典、應用最為廣泛的一種。該理論認為結構在經歷多級應力循環后產生的損傷量為
(4)
式中:ni為對應當前應力水平si下的實際循環數;Ni為材料應力幅值為si時的疲勞壽命。
而ni,Ni可表示為
ni=E(P)·T·P(si)·Δsi
(5)
(6)
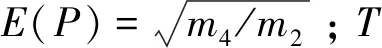
將式(5)、式(6)代入式(4),并把求和換成積分得到

(7)
當結構某位置的損傷量D=1時,認為結構該位置發生疲勞破壞,由此推出結構的疲勞壽命
(8)
2 姿控系統連接螺釘計算模型
某姿控動力系統在經歷y向隨機振動試驗(5 min)后,經檢查未發現異常,繼續完成z向隨機振動試驗(5 min),直到該試驗結束后才發現連接螺釘出現了疲勞斷裂,如圖1所示。

圖1 振動斷裂的螺釘結構Fig.1 The broken screw in vibration
該姿控動力系統主要包括貯箱、氣瓶、框架、底板及連接螺釘,連接螺釘起到框架與底板的連接作用,模型如圖2所示,其中,坐標系以推力方向為x向,框架上端長邊法蘭為z向,按右手準則確定y向。試驗中,振動激勵由振動臺通過試驗工裝傳到框架法蘭及底板外側,因此,隨機振動加速度激勵加載于此。各組件材料及其力學性能參數如表1所示。
3 結構模態仿真結果
通過y、z方向10~2 000 Hz范圍的頻響分析可知,結構響應主要出現在500 Hz以下。因此,重點分析500 Hz以下姿控動力系統的模態[11],計算得到振動試驗狀態下結構的前9階模態頻率及模態振型,如表2所示。
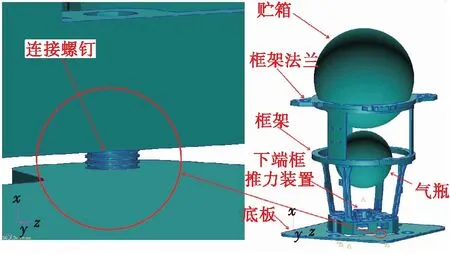
圖2 姿控動力系統結構有限元模型 Fig.2 The finite element model of DACS
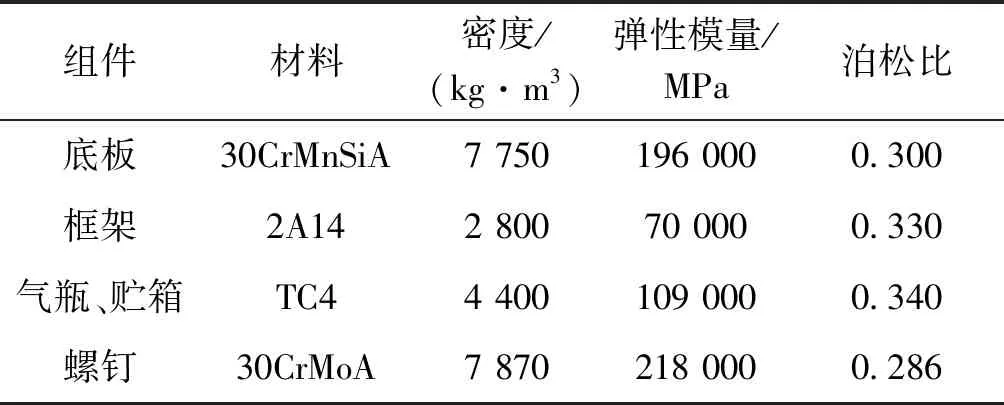
組件材料密度/(kg·m3)彈性模量/MPa泊松比底板30CrMnSiA7 750196 0000.300框架2A142 80070 0000.330氣瓶、貯箱TC44 400109 0000.340螺釘30CrMoA7 870218 0000.286
表2 振動試驗狀態姿控動力系統模態計算結果
Tab.2 Modal calculation results of the DACS in the vibration test state
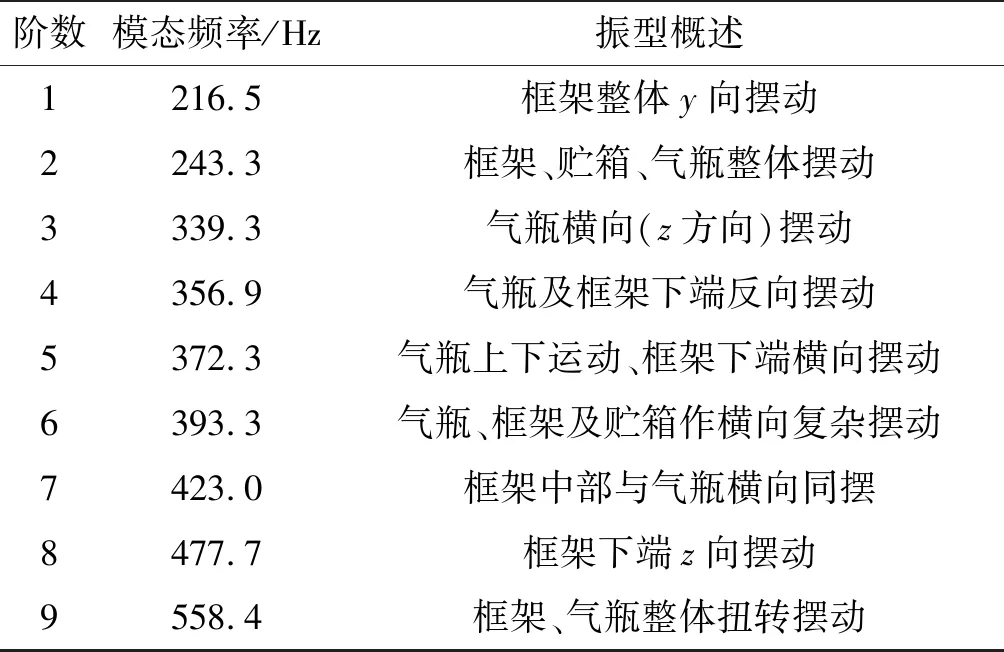
階數模態頻率/Hz振型概述1216.5框架整體y向擺動2243.3框架、貯箱、氣瓶整體擺動3339.3氣瓶橫向(z方向)擺動4356.9氣瓶及框架下端反向擺動5372.3氣瓶上下運動、框架下端橫向擺動6393.3氣瓶、框架及貯箱作橫向復雜擺動7423.0框架中部與氣瓶橫向同擺8477.7框架下端z向擺動9558.4框架、氣瓶整體扭轉擺動
為了解哪些模態在隨機振動環境下會對連接螺釘產生較大的應力,分別提取前9階模態單獨產生的結構應力響應及全模態應力響應,并基于第1節介紹的振動疲勞壽命估算方法分別進行損傷計算與分析,結構系統模態振型如圖3~圖5所示。
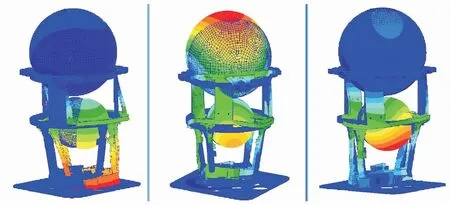
圖3 結構系統前3階模態振型Fig.3 The first three modal shapes of the structure model
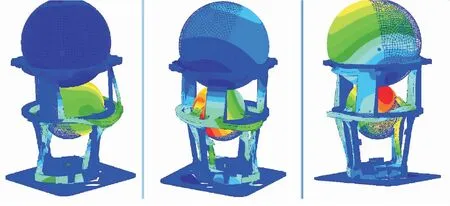
圖4 結構系統第4至第6階模態振型Fig.4 The fourth to sixth modal shapes of the structure model
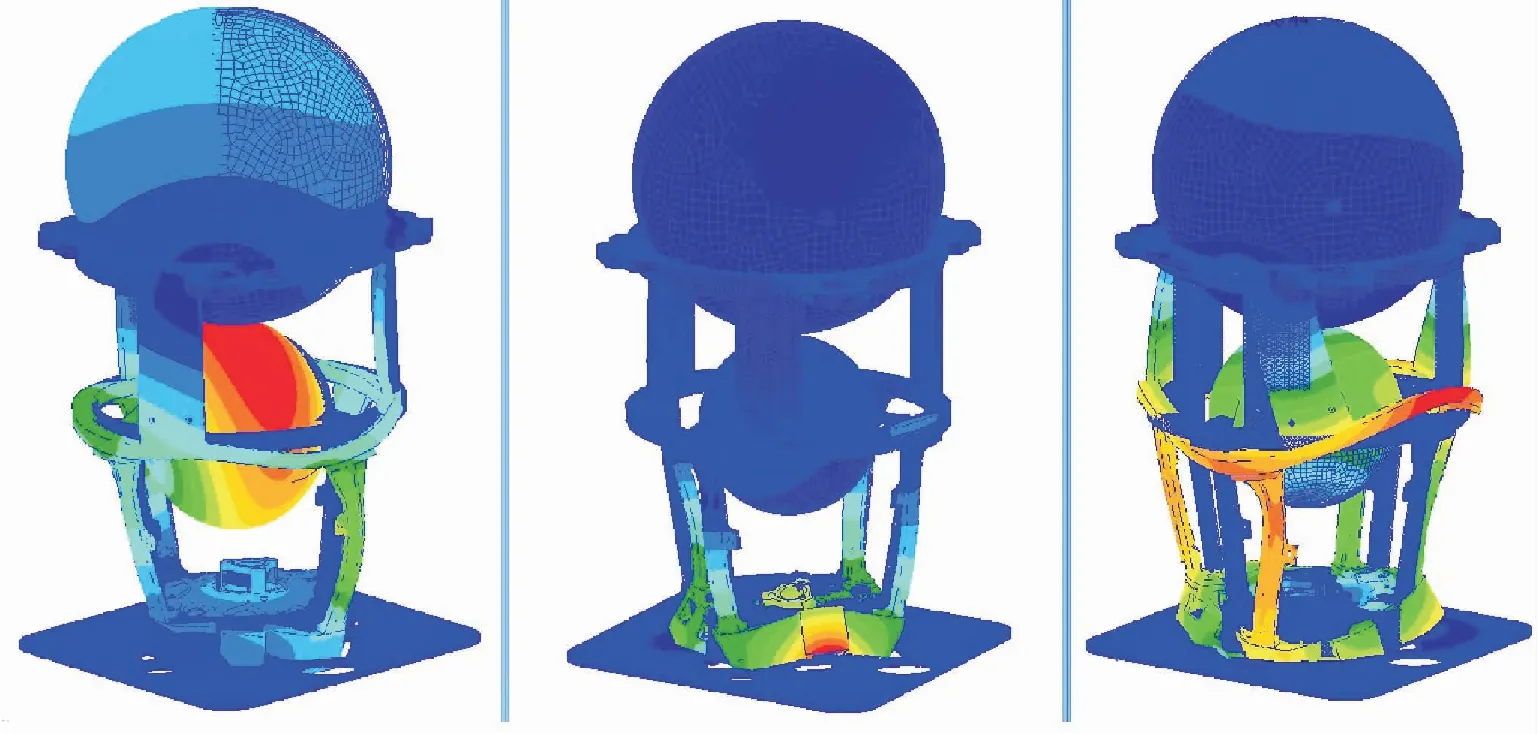
圖5 結構系統第7至第9階模態振型Fig.5 The seventh to ninth modal shapes of the structure model
4 隨機振動疲勞損傷計算
為了得到全模態及各階單模態在振動試驗環境下對連接螺釘產生的損傷,首先需要得到振動激勵條件下全模態及各階單模態引起的應力功率譜密度函數,這可通過有限元求解器Nastran進行模態法頻域響應及隨機振動的計算獲得[12-13]。計算中,各階模態阻尼采用0.03,隨機振動輸入條件如圖6所示,試驗仿真分兩個方向(y、z),每個方向5 min。
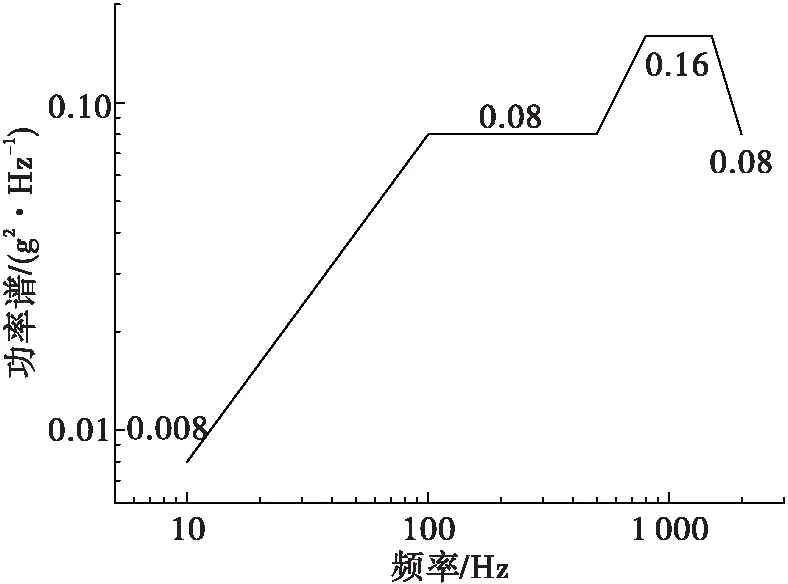
圖6 隨機振動試驗條件Fig.6 Random vibration test input condition
經過計算,得到結構分別在y,z隨機振動環境下連接螺釘斷裂位置的應力功率譜密度函數,如圖7、圖8及圖9所示,其中,y向隨機振動中連接螺釘斷裂位置附近應力RMS值分布如圖10所示。實際結構工作過程或振動試驗通常均表現為多軸應力問題,而目前求解多軸疲勞問題的一類方法是將多軸應力問題等效為單軸應力問題[14-17]。根據計算出的應力功率譜,應用式(7)和式(8)得到相應的損傷量D及壽命Ts,結果如表3所示。其中,參數m,C通過對材料應力壽命數據的擬合得到,m=13.9、C=7×1 043。另外,表3中總壽命計算結果表示姿控動力系統經歷了391.9 s的y向隨機振動后,再經歷391.9 s的z向隨機振動,連接螺釘就發生結構疲勞斷裂。
計算結果表示:在經歷連續兩個方向的隨機振動試驗后,姿控動力系統連接螺釘斷裂位置處的疲勞損傷量D達到0.765 4,距離理論上結構發生疲勞破壞時D=1存在一定出入,分析的主要原因為:文中采用的振動疲勞壽命評估方法本身具有統計特性,個例結果具有一定的散差。
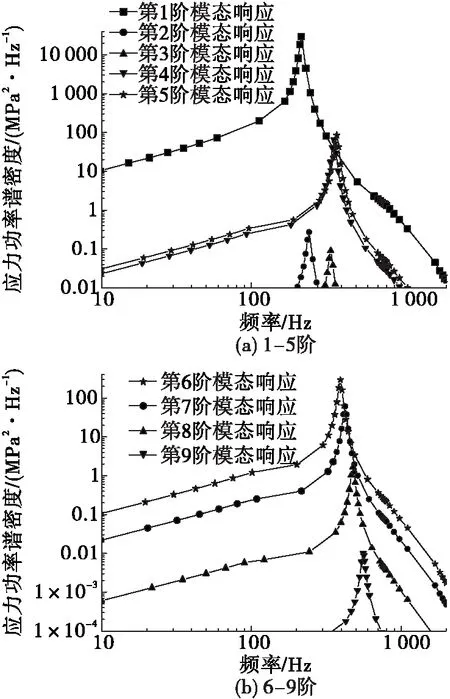
圖7 y向隨機振動單階模態應力響應功率譜密度曲線Fig.7 The stress power spectral of single mode response in the y direction random test
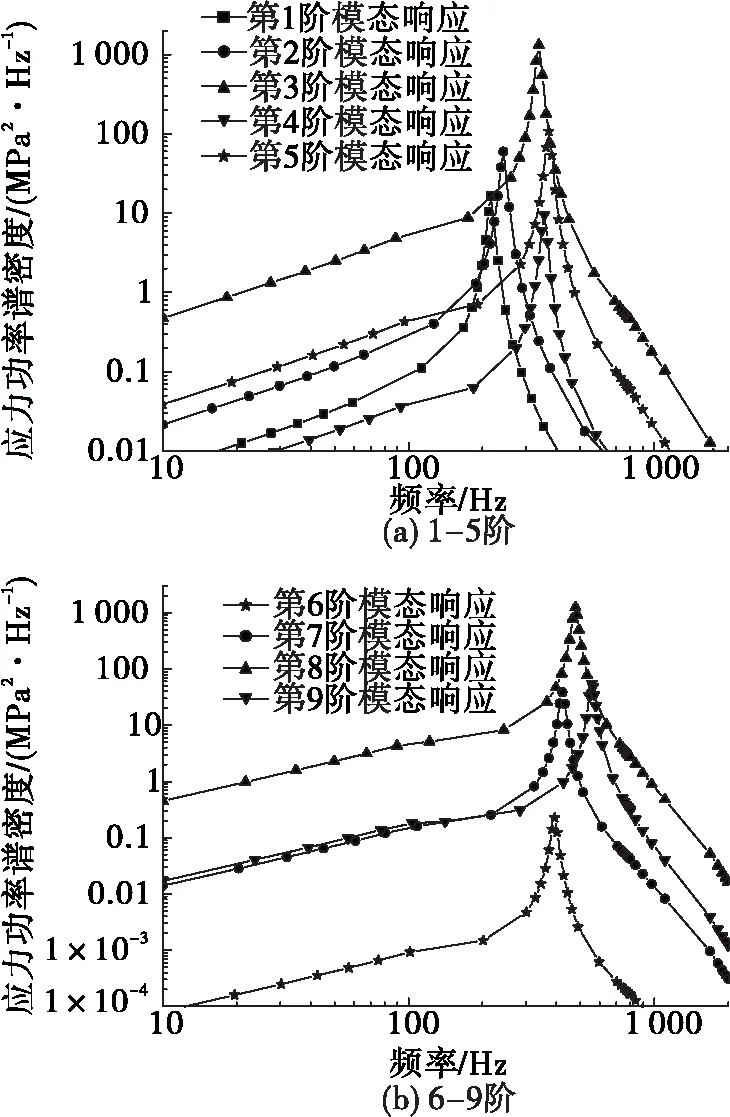
圖8 z向隨機振動單階模態應力響應功率譜密度曲線Fig.8 The stress power spectral of single mode response in the z direction random test
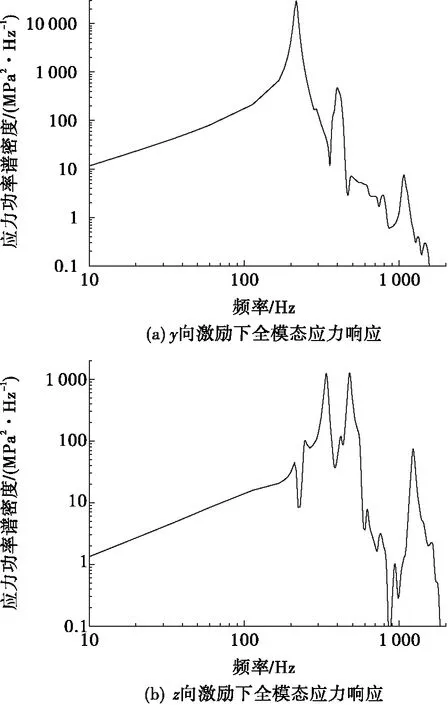
圖9 隨機振動中全模態應力響應功率譜密度曲線 Fig.9 The stress power spectral of full mode response in the random test
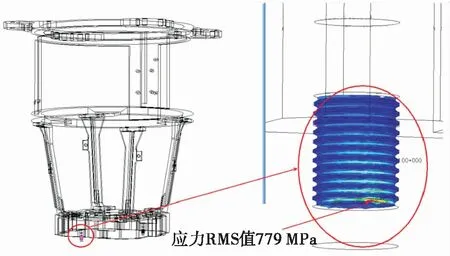
圖10 y向隨機振動中連接螺釘斷裂位置應力RMS值分布 Fig.10 The stress RMS distribution of the broken screw during y direction random test
另外,不同方向的隨機振動,各階模態對螺釘振動斷裂的影響大小不一樣,其中,y向隨機振動中第1階模態產生的損傷較大,而z向隨機振動中第3階、第8階模態影響更大,因此,在后續的防護和結構改進中應重點關注以上3階模態。
從表3的應力RMS值與損傷量的對應關系來看,較大的應力RMS值通常也會產生較大的疲勞損傷量,因此,工程上常依據仿真得到的應力RMS值的相對大小來定性地評估結構在隨機振動試驗中的危險部位[18]。其實,這并不充分,如y向隨機振動中第1階模態產生的應力RMS值比z向隨機振動中第8階模態大,但損傷量卻比較小。
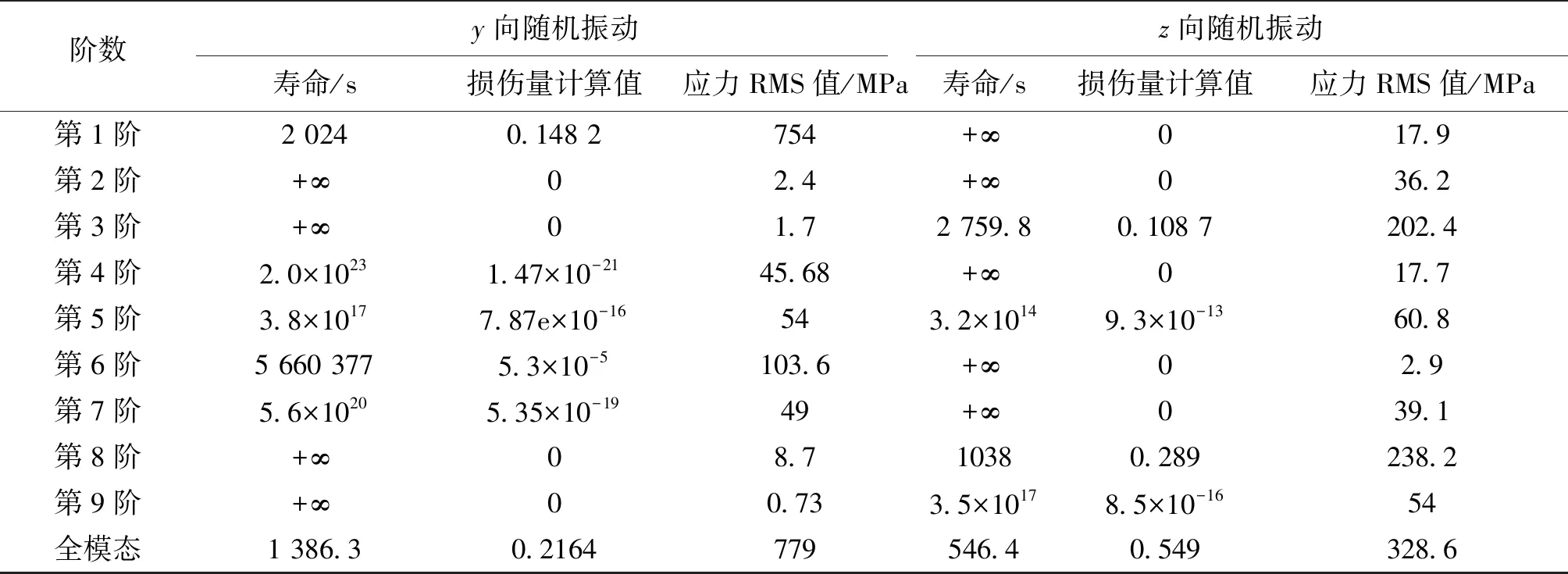
表3 隨機振動環境下螺釘斷裂位置疲勞損傷量及壽命計算結果
5 結論
通過仿真分析可以得到以下主要結論:
1)在經歷連續兩個方向的隨機振動試驗后,姿控動力系統連接螺釘斷裂位置處的疲勞損傷量D達到0.765 4,雖然離D=1存在一定距離,但仍是一個比較大的損傷量,與試驗結束后螺釘疲勞斷裂的現象基本吻合。
2)通過單階模態響應的損傷量計算,可以得到各階模態對結構振動疲勞斷裂的影響大小,從而找出影響較大的部分模態,為結構改進及抗疲勞設計提供參考。
3)僅僅依靠應力RMS值的相對大小來評估結構在隨機振動試驗中的危險部位是不充分的,更好的做法是把具有較大應力RMS值的位置都進行疲勞損傷量計算,再根據計算結果進行定量評估。

