基于貪婪算法的無人機運輸方案研究

侯志浩 吉林大學數學學院

引言

2017 年，美國波多黎各領土遭遇了最嚴重的颶風，對數百萬居民造成了巨大的不利影響。由于許多高速公路已經中斷，所以各地居民迫切需要救生醫療用品。在這種情況下，非政府組織提出了“Dronego”項目，將無人機的3 個醫療包轉移到5 家選定的醫院。我們需要設計一個從已確定的各種候選旋翼無人機中選出的“DroneGo”機隊，以完成轉移醫療包和檢測道路狀況的任務。

1 初步分析

我們利用經度作為橫坐標，緯度作為Y 軸坐標來獲得圖1，因此我們可以直觀地指出5 個位置的分布。當然，實際位置位于拱形，而我們的坐標圖是平坦的。事實上，我們的地圖是地球的一個橫截面，因此可能與直覺中的真實地圖有所不同，但距離，經度和經度都是準確的值。

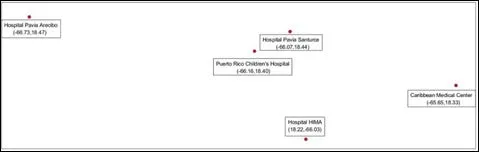
圖1 波多黎各的坐標圖顯示了5 個目的地

首先，我們給出以下定義：

獨立需求（di）：相應中心每天對醫療包的需求。總需求（S）：每天醫療包5 個中心需求的總和。

隨后，我們將醫療中心的比例系數定義為：

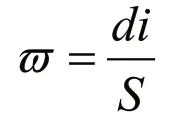
在我們看來，這個定義是合理的，因為每個中心需要的包裹數量與其接納人口，各種醫療水平的指數正相關。該系數表明了相應醫療中心在緊急情況下的重要性。然后我們定義了另一個公式來比較任何兩個災害應對方案。首先，我們給出以下定義：

然后得到：

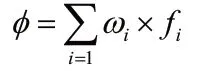
2 分類討論

到目前為止，我們已經確定了車隊，考慮到每個位置的最佳距離不是唯一的，我們將ISO 容器作為圓心，找到交叉區域后，覆蓋道路，人口和地形做出選擇。最佳位置是（見圖2 和圖3）

圖2 最佳位置

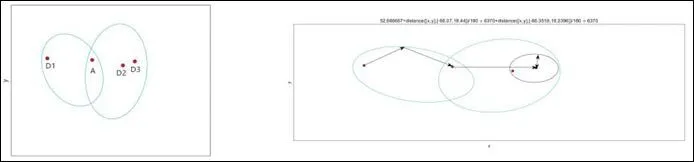
圖3 平面圖中的最佳位置

如圖3 所示，我們可以要求無人機可以從A 點出發，并在到達由A點和醫院確定的橢圓的任何點后到達醫院，如果可能的話，保持飛行剩余距離的一半到任何要求的地方，最后回到醫院。（如（b）所示）

球場并不總是直的，無人機可以在曲線路線上飛行，只要它們可以返回（醫院或集裝箱）至于VRD（視頻偵察無人機），可檢測區域是如上所述的偵察圈（SC）。

草圖僅顯示兩個不同的路線以給出簡單的符號。坐標由經度和緯度組成，這使得性能不像現實那么直觀。

3 結論

對于前往D1 的無人機，每架無人機B 最多可以滿足D1 的2 天要求，所以我們只需要在兩天內發送一架無人機B.對于支持D2 的無人機，每架無人機F最多可以滿足一天的請求，并有足夠的空間來攜帶MED包，比例為202/112/211，因此我們可以在前兩天指定一架無人機F，然后發送其余要求的4 天（此外，無人機可以在一次飛行中提供D3 和D2，我們可以通過這種方式實現D1 和D2 的包裝管理）。在考慮D3 時，每架無人機B 最多可以滿足一天的要求。根據比例系數，我們只需在四天內分配一架無人機。