多傳感器數據關聯方法

呂奇辰 中國人民解放軍93117 部隊

引言

多目標實時跟蹤過程中，多個傳感器對同一目標的測量數據，具有相似特征，但雜波干擾和傳感器的測量誤差，使得測量數據的特征不完全相同，利用相似特征來判定量測數據的來源就是數據關聯方法。

數據關聯通常分為幾種方式，其中觀測/點跡與觀測/點跡關聯、觀測/點跡與航跡關聯，一般用于集中式結構；而在分布式信息處理系統中多采用航跡與航跡關聯。三種方式都存在于多傳感器系統中，按照給定的準則，對數據進行處理，去除干擾數據，實現對航跡的初始化，即為數據關聯的任務。

1 集中式數據關聯方法

1.1 最近鄰域數據關聯(NNDA)

最近鄰域數據關聯算法屬于數據挖掘技術，是最簡單、最有效、最早提出的數據關聯方法之一。如圖1 所示，NNDA 中的N 表示統計距離達到最小或是殘差概率密度為最大。

圖1 最近鄰域數據關聯

該方法適用于跟蹤目標稀疏的情況，是一種局部最優的“貪心算法”，NNDA 算法的運算量小，易于實現，但在雜波干擾或者目標密集的情況下，錯誤關聯較多。

1.2 聯合概率數據關聯(JPDA)

JPDA 是Bar Shalom 等人提出的一種數據關聯算法，當觀測數據落入跟蹤門相交區域時，表示這些觀測數據可能來源于多個目標。JPDA 計算觀測數據與每一個目標之間的關聯概率，認為所有的有效回波都源于每個特定目標的概率不同。在雜波環境中JPDA 方法對多目標跟蹤的結果較為理想，不需要任何關于目標和雜波的先驗信息，但目標和量測數目增多時，與其他算法相比，計算比較復雜，算法詳見文獻。

2 分布式航跡關聯方法

考慮到系統中分布于不同位置的傳感器，其信息處理系統的航跡是否具有唯一目標指向性，傳感器覆蓋范圍內是否存在重復跟蹤目標的問題，航跡關聯算法可以分為基于統計和基于模糊數學的算法。

2.1 基于統計的算法

航跡關聯問題可以通過不同的檢驗統計轉化成假設檢驗問題，如加權修正法、最近鄰域法、序貫法和雙門限法等。加權修正法在密集目標環境下關聯性能下降，在交叉和分岔航跡較多的場合會出現較多錯漏關聯航跡，最近鄰域法也存在錯漏關聯航跡的情況，序貫算法和雙門限算法能較好的修正這個問題。

(1)加權修正

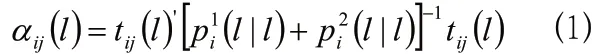
當航跡估計誤差間不獨立時，可以修正檢驗統計量為：

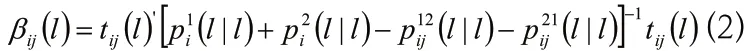
(2)最近鄰域法

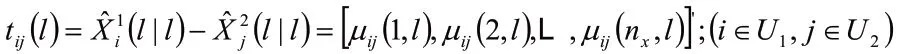
(3)序貫法和雙門限法

序貫法考慮歷史航跡，改善了加權修正法的問題。該算法來源于雷達信號中的序貫檢測。

雙門限法，需要設定計數器T，流程如圖2 所示，對R 個估計誤差樣本（系統中兩個任意節點），逐個基于X2分布門限進行假設檢驗，若判定為同一目標的航跡，則T=T+1，否則T 不變。將T 與指定的數 L 進行比較，經過R 次檢驗后，如果T ≥L，航跡關聯判決結束，否則判定為不關聯航跡。

圖2 雙門限法流程圖

2.2 基于模糊數學的航跡關聯方法

在某些場合中，例如目標密集、隨機目標較多、存在較多分岔航跡或者系統中存在較大導航誤差、傳感器校準誤差、傳感器轉換和延遲誤差，用統計學方法來判斷航跡關聯性是很困難的，不能滿足實際要求。

考慮到在航跡關聯判決中的模糊性，可以用隸屬度函數來界定兩個航跡的相似程度，這種方法可以稱之為模糊航跡關聯法。可細分為模糊函數法和模糊邏輯法，其特點見表1。

表1 基于模糊數學的航跡關聯法

3 結論

航跡關聯問題在傳感器的間距遠或沒有干擾時，比較簡單。對于多目標、噪聲、多交叉及分岔航跡的情況，就會比較困難。再考慮更實際的狀況，比如傳感器組合失配、傳感器位置誤差、監測目標的誤差，航跡關聯問題就更為復雜。

文中提到的加權修正法等統計方法均是在某時刻就做出最終判決，準確度不可控。概率數據關聯算法或者將各種算法進行組合優化，會相對完善，但是目標增多時，計算量會劇增，應進一步探討簡單實用的關聯方法。