距離模糊下天空雙基地預警雷達雜波抑制方法

(空軍預警學院，湖北武漢 430019)

0 引 言

天空雙基地預警雷達將發射端置于衛星上，接收端置于預警機或無人機上[1-2]，具有典型的雙基地雷達特點，同時由于各部分相對運動關系復雜，影響因素較多，使得地面雜波呈現嚴重的非平穩性[3]。在進行空時自適應處理(STAP)時，難以準確估計待檢測單元的雜波協方差矩陣，導致抑制凹口變形展寬，STAP性能下降，嚴重影響了雜波抑制效果和對慢速目標的檢測能力。

為了抑制雙基地機載雷達以及非正側面陣單基地機載雷達帶來的非平穩雜波，提出了導數更新法(DBU)、多普勒頻移法(DW)、聯合時間訓練樣本法(JTTS)等多種方法[5-7]。其中，導數更新法將自適應權矢量與距離變化聯系起來進行非平穩雜波抑制；多普勒頻移法在準確計算出每個距離環方位-多普勒曲線的基礎上，利用多普勒頻移實現雜波抑制；聯合時間訓練樣本法通過減少距離向的訓練樣本降低雜波非平穩性的影響，從而實現雜波抑制。但這些方法都沒有考慮距離模糊的影響，當距離模糊存在時，近程雜波和遠程雜波疊加在一起，使用上述方法時會導致雜波協方差矩陣估計失準，影響抑制效果[8-9]。基于此，本文提出一種距離模糊非平穩雜波抑制方法[10]，既能有效抑制天空雙基地預警雷達非平穩雜波，同時又考慮了距離模糊的影響。

1 天空雙基地預警雷達幾何模型

天空雙基地預警雷達的幾何關系如圖1所示，T代表衛星發射端，B為衛星星下點，ht為衛星軌道高度，vt為衛星飛行速度大小，θaz代表衛星發射波束相對于衛星速度的方位角，θel為衛星發射波束的下視角，φt為衛星發射波束擦地角，Rt為發射距離，C為地面雜波散射點，R代表空基接收端，D為空基接收端的地面投影，θrz代表接收波束方位角，θrl代表接收波束下視角，φr為接收波束擦地角，hr為空基接收端高度，vr為空基接收端速度大小，Rr為接收距離,Re為地球半徑。

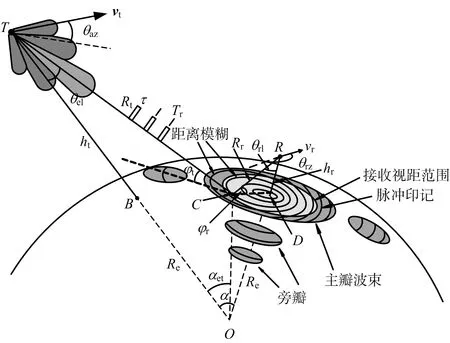
圖1 天空雙基地預警雷達幾何關系

不同于單基地雷達，在天空雙基地預警雷達系統中，信號傳播距離為衛星發射端T到雜波散射點C的距離與雜波散射點C到空基接收端R的距離之和。相應的角度關系以及距離和如下：

在發射三角形TOC中，由正弦定理可得

(1)

衛星波束下視角θel為

(2)

則衛星的發射球心角αet為

αet=π-θel-∠TCO=π-θel-

(3)

從而，發射距離Rt為

Rt=Resinαet/sinθel

(4)

接收距離Rr為

(5)

式中，(α2,β2)和(α3,β3)分別代表地面雜波散射點C和當前時刻空基接收端R的地理緯度和經度對應的弧度。

收發距離和Rs為

Rs=Rt+Rr=Resinαet/sinθel+

(6)

2 考慮距離模糊時的天空雙基地預警雷達雜波模型

2.1 雜波單元劃分

如圖2所示，在天空雙基地預警雷達空基接收端的視距范圍內，將地面劃分為一系列等距離環，每條等距離環上的散射點對應的收發距離和相同，這里的ΔR指相鄰兩個等距離環對應的收發距離和的差值，即雷達距離分辨率。對于線性調頻信號，脈沖壓縮之后的距離分辨率為

(7)

式中，c代表光速，Bn代表線性調頻信號的帶寬。

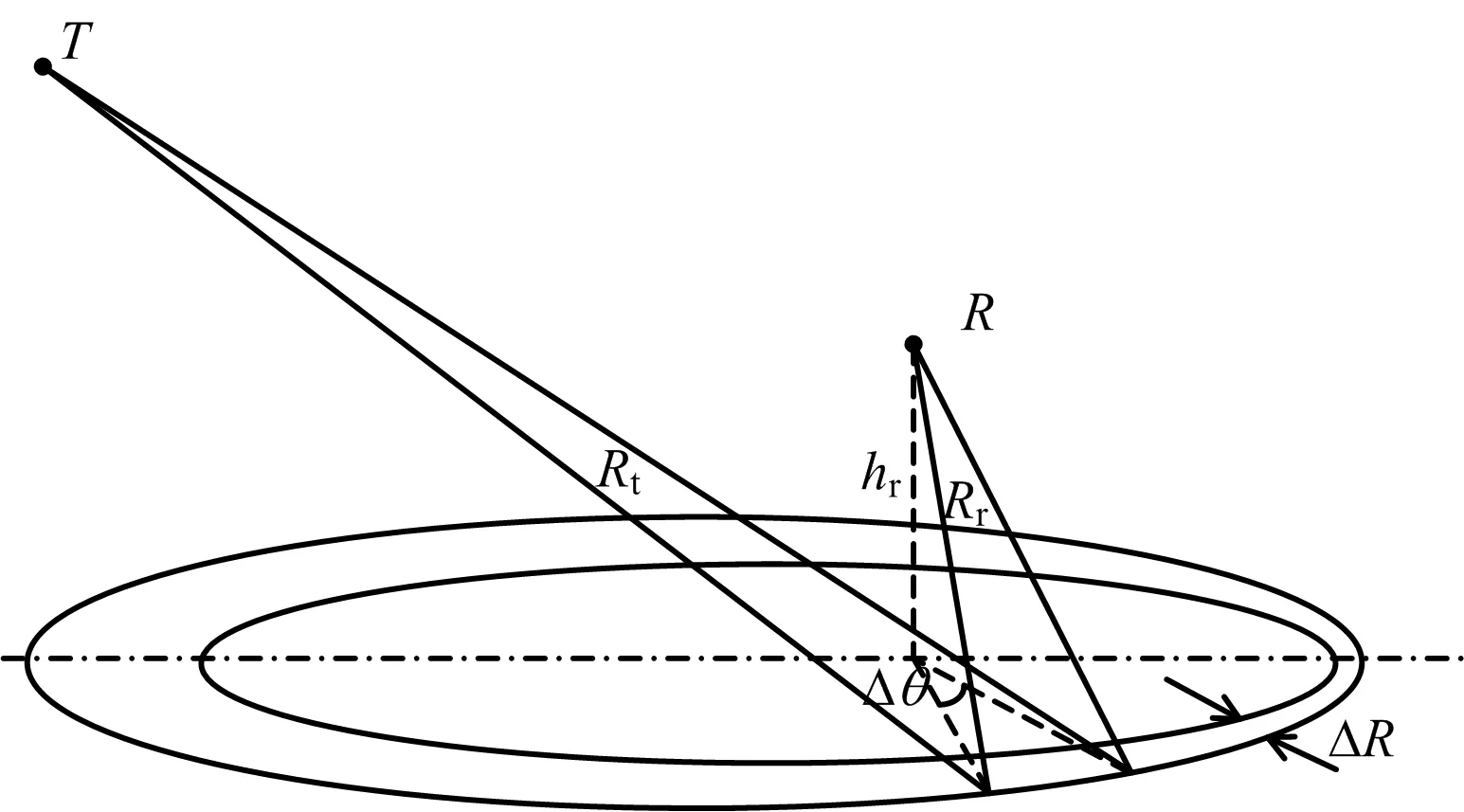
圖2 雜波單元劃分圖

2.2 距離模糊

天空雙基地預警雷達最大不模糊距離Ru=c/fr，在空基接收端接收范圍內，收發距離和最大為Rmax，最小為Rmin，則等距離環數M和距離模糊數L分別為

(8)

(9)

式中，floor(·)表示向下取整。

2.3 考慮距離模糊時的雜波模型

假設雷達接收天線采用N路通道的矩形正側面陣，經過列向合成后，進行N點空域采樣和K(時域脈沖數)點時域采樣，Cm表示第m個距離環雜波采樣信號，則Cm可用(NK×1)維的空時采樣信號的數據矩陣表示：

Cm=[cm(1,1) …cm(N,1) …

cm(1,K) …cm(N,K)]T

(10)

式中，cm(n,k)表示第n列陣元在第k個時刻對第m個距離環的空時二維采樣數據，其表達式為

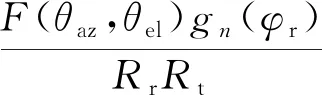
j(k-1)ωt(θrz,φr)]dθrz

(11)

式中，

(12)

(13)

式中，n=1,2,…,N，k=1,2,…,K，m=1,2,…,M，d為陣元間距，F(θaz,θel代表發射方向圖，gn(φr)代表接收方向圖，ωs(θrz,φr)代表空間角頻率，ωl(θrz,φr)代表時間角頻率，fd(θrz,φr)為對應雜波單元的多普勒頻率，fr代表脈沖重復頻率。

為了不產生多普勒模糊，天空雙基地預警雷達采用的脈沖重復頻率較高，相比傳統地基和空基雷達，最大不模糊距離較短，加上探測范圍大，距離模糊較為嚴重。假設在探測范圍內地面回波出現L次距離模糊，則接收回波中雜波的協方差函數變為

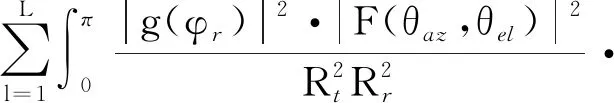
exp[jΔnωs+jΔkωt]dθrz

(14)

2.4 雜波特性對STAP性能的影響

在天空雙基地預警雷達中，雜波和噪聲的相關矩陣為

R=E{(Cm+n)(Cm+n)T}=Rm+σ2I

(15)

式中σ2代表噪聲方差，I為NK×NK的單位矩陣，Rm為雜波協方差矩陣。由于真實的雜波協方差矩陣Rm是未知的，需要進行估計，通常由臨近距離單元估計得到，即

(16)

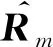
3 考慮距離模糊的非平穩雜波抑制方法

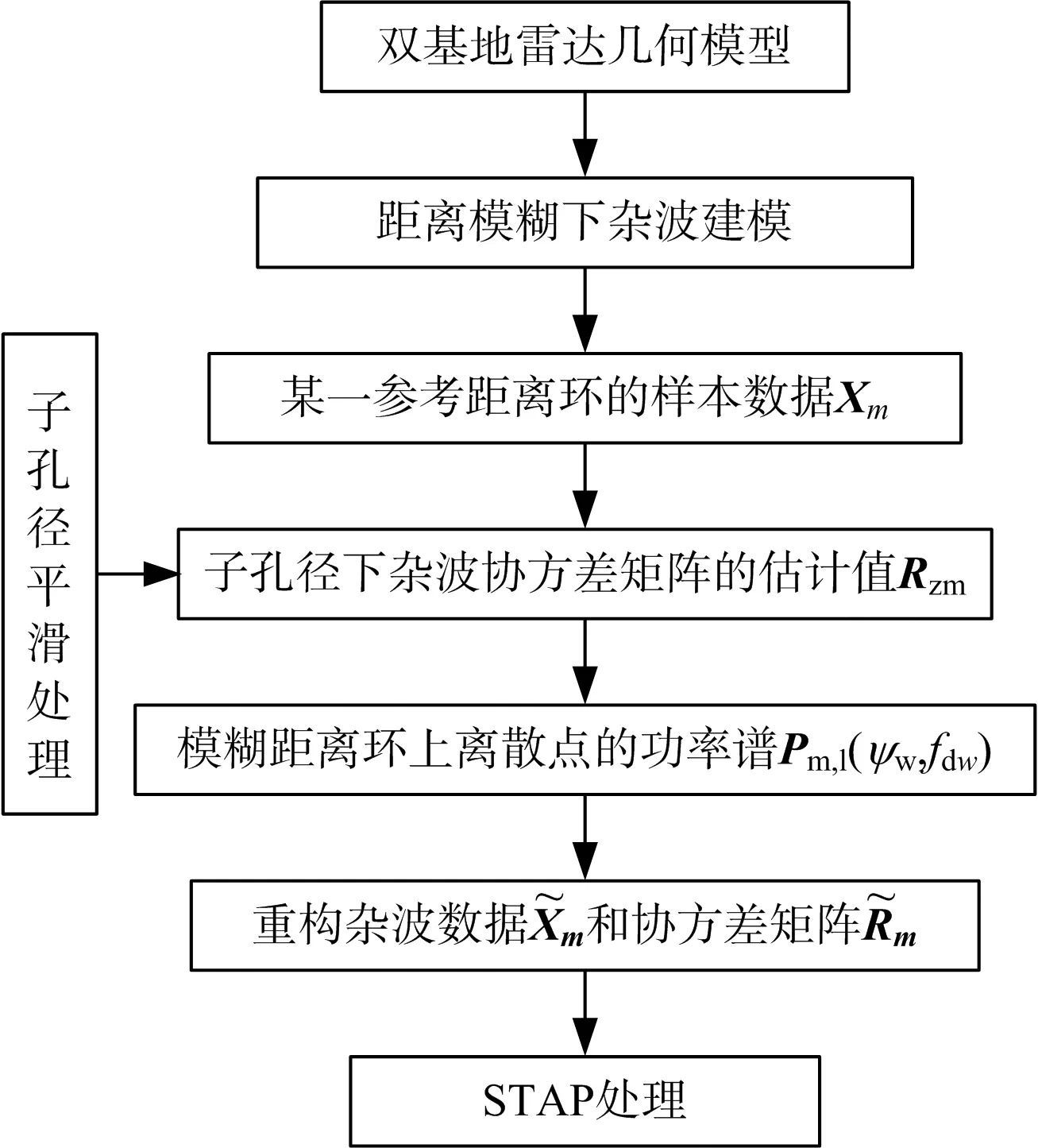
圖3 天空雙基地預警雷達非平衡雜波處理步驟

為了有效抑制天空雙基地預警雷達非平穩雜波，本文提出一種基于子孔徑平滑和重構雜波數據的補償方法。首先對指定距離環數據進行空時子孔徑平滑，犧牲陣列孔徑以產生大量回波數據，同時減小非平穩性的影響，從而估計出該距離環在子孔徑下的雜波協方差矩陣。然后，在該距離環上取一些離散點，計算功率譜作為其幅度值。再利用該距離環功率譜重構各模糊距離環的回波數據和雜波協方差矩陣，最后進行空時自適應處理，具體實現步驟如圖3所示。該方法充分考慮雜波非平穩性以及距離模糊的影響，從而對天空雙基地預警雷達雜波進行抑制。

3.1 子孔徑平滑

空基接收端對第m個距離環的空時采樣數據Xm∈CN×K可以表示為

(17)

為了保證協方差矩陣估計的精確性，必須擁有足夠多的距離環數據，而天空雙基地預警雷達對距離環的快拍數有限，難以獲得充足的數據量。為解決這一問題，首先對某一距離環的回波數據進行空間和時間子孔徑平滑，取空間子孔徑為G，時間子孔徑為J，經過空間子孔徑平滑，得到(N-G+1)(K-J+1)個矩陣Qg,j∈CG×J：

g=1,…,N-G+1;j=1,…,K-J+1

(18)

經過子孔徑平滑后，樣本數據量明顯增大，利用這些樣本數據可以計算得到雜波協方差矩陣子孔徑下的估計值Rzm∈CGJ×GJ

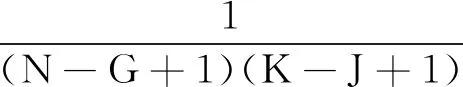
(19)

式中，(·)H表示轉置共軛，Vec(·)表示將矩陣按照列的順序變換成一個列矢量。

3.2 重構協方差矩陣

在重構數據時，考慮各個模糊距離環的影響，通過計算每個模糊距離環的功率譜來重構出雜波協方差矩陣。首先計算功率譜，在第m個距離環的第l次模糊距離環上均勻取W個離散點(W>2NK)，其功率譜Pm,l(ψw，fdw)的表達式為

(20)

式中，ψw和fdw分別代表離散點對應的空間錐角和多普勒頻率，Szl(ψw，fdw)代表離散點在子孔徑下的空時二維導向矢量，其表達式為

Szl(ψw，fdw)=Szl(ψw)?Szl(fdw)=

(21)

式中，Szl(ψw)和Szl(fdw)分別代表雜波空域和時域導向矢量，?表示Kronecker積。

(22)

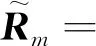
(23)

式中，Sl(ψw，fdw)為離散點在空時平面上的空時導向矢量，其表達式為

Sl(ψw，fdw)=

(24)

3.3 STAP處理

利用式(23)得到的重構協方差矩陣對天空雙基地預警雷達距離模糊雜波進行空時自適應處理，選擇線性處理器權矢量：

(25)

式中，s為空時導向矢量。改善因子為

(26)

式中，tr(·)表示矩陣的跡。

4 仿真分析

仿真時具體仿真參數如表1所示。

4.1 距離模糊對雜波功率譜的影響

圖4(a)和圖4(b)比較了在不考慮距離模糊和考慮距離模糊時1 200 km處的雜波功率譜的分布情況。可以看出，考慮距離模糊時，近距離的雜波和遠距離的雜波疊加在一起，雜波的幅度和范圍比單距離環時明顯變大，頻譜嚴重展寬。

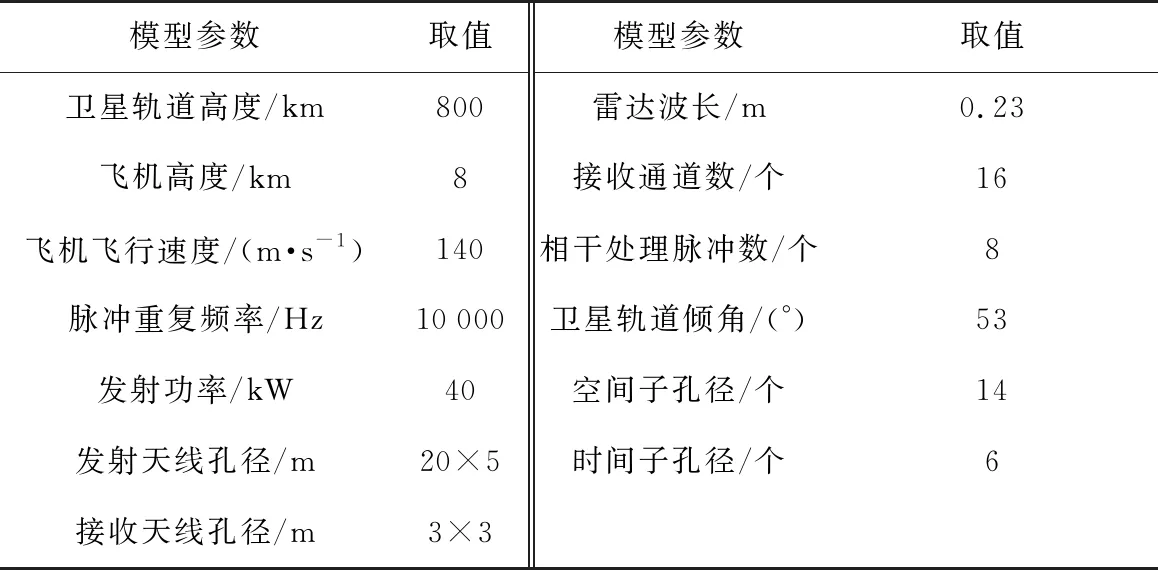
表1 天空雙基地預警雷達系統模型參數

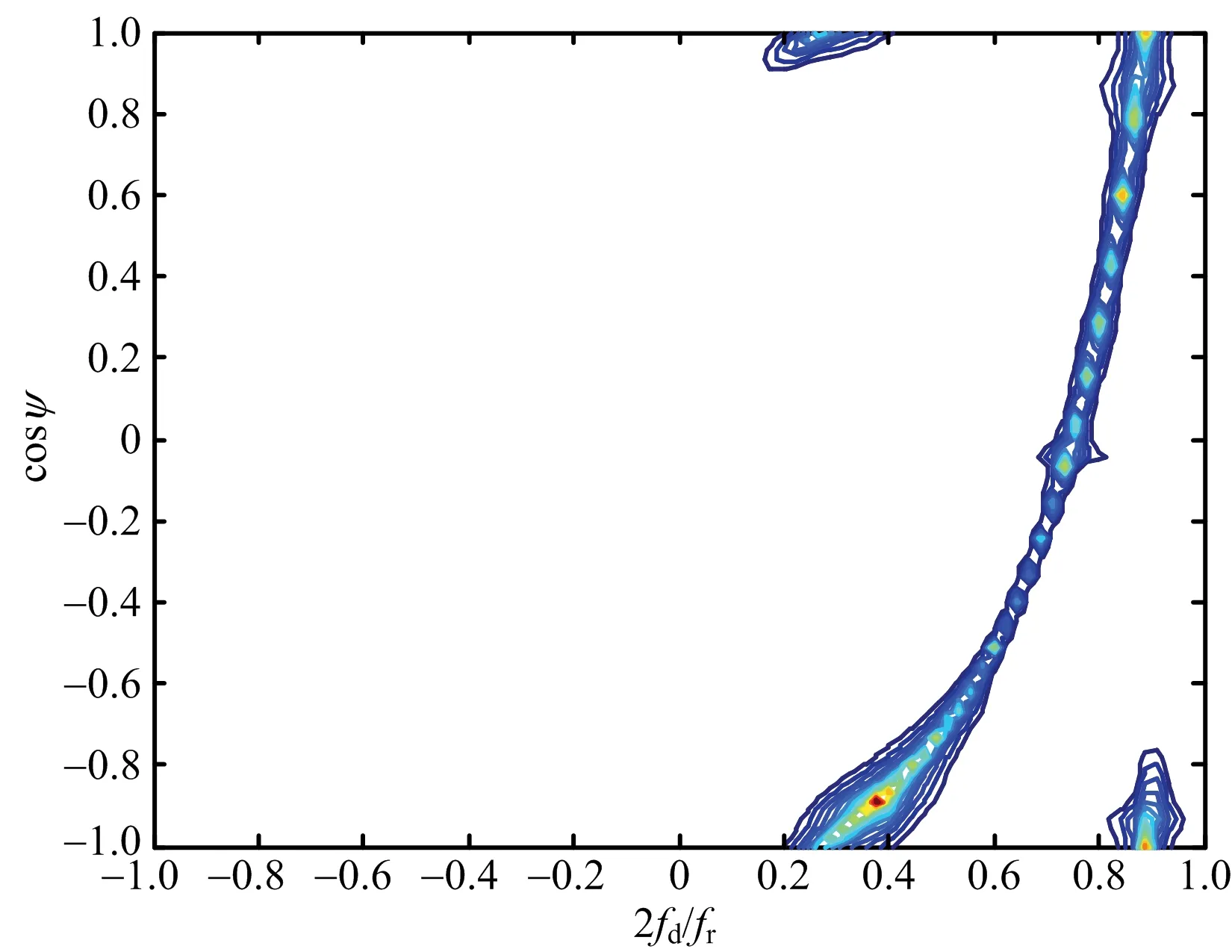
(a) 不考慮距離模糊

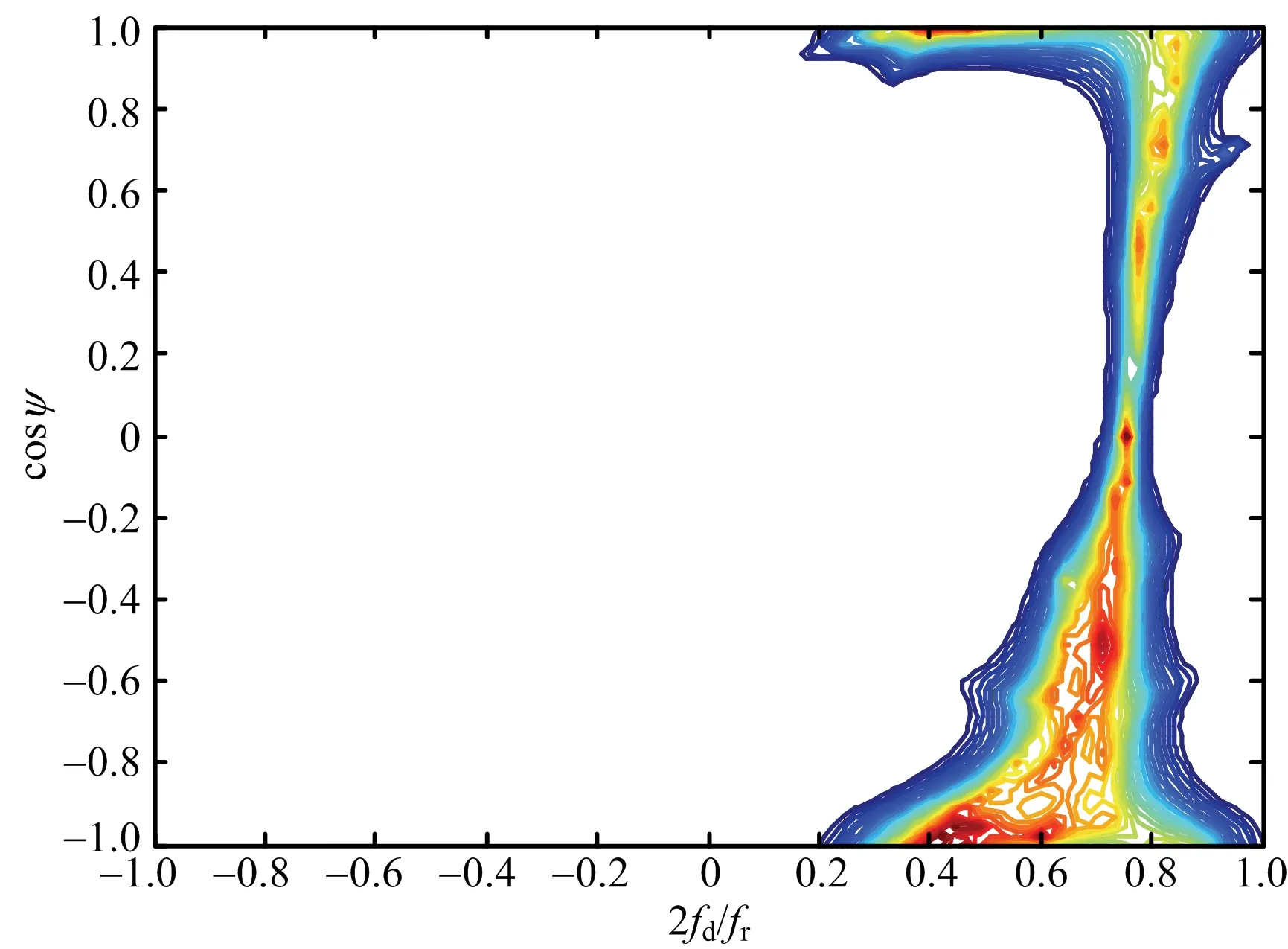
(b) 考慮距離模糊圖4 1 200 km處的雜波功率譜

4.2 重構功率譜仿真

利用式(23)可以得到重構的雜波協方差矩陣，在重構時將雜波非平穩性和距離模糊都考慮在內，通過雜波協方差矩陣得到重構雜波功率譜，圖5～圖7為不同收發球心角下同一距離環的理論功率譜與重構功率譜。

通過對比圖5～圖7可以得出，利用本文方法重構出的雜波協方差矩陣與理論值十分接近。

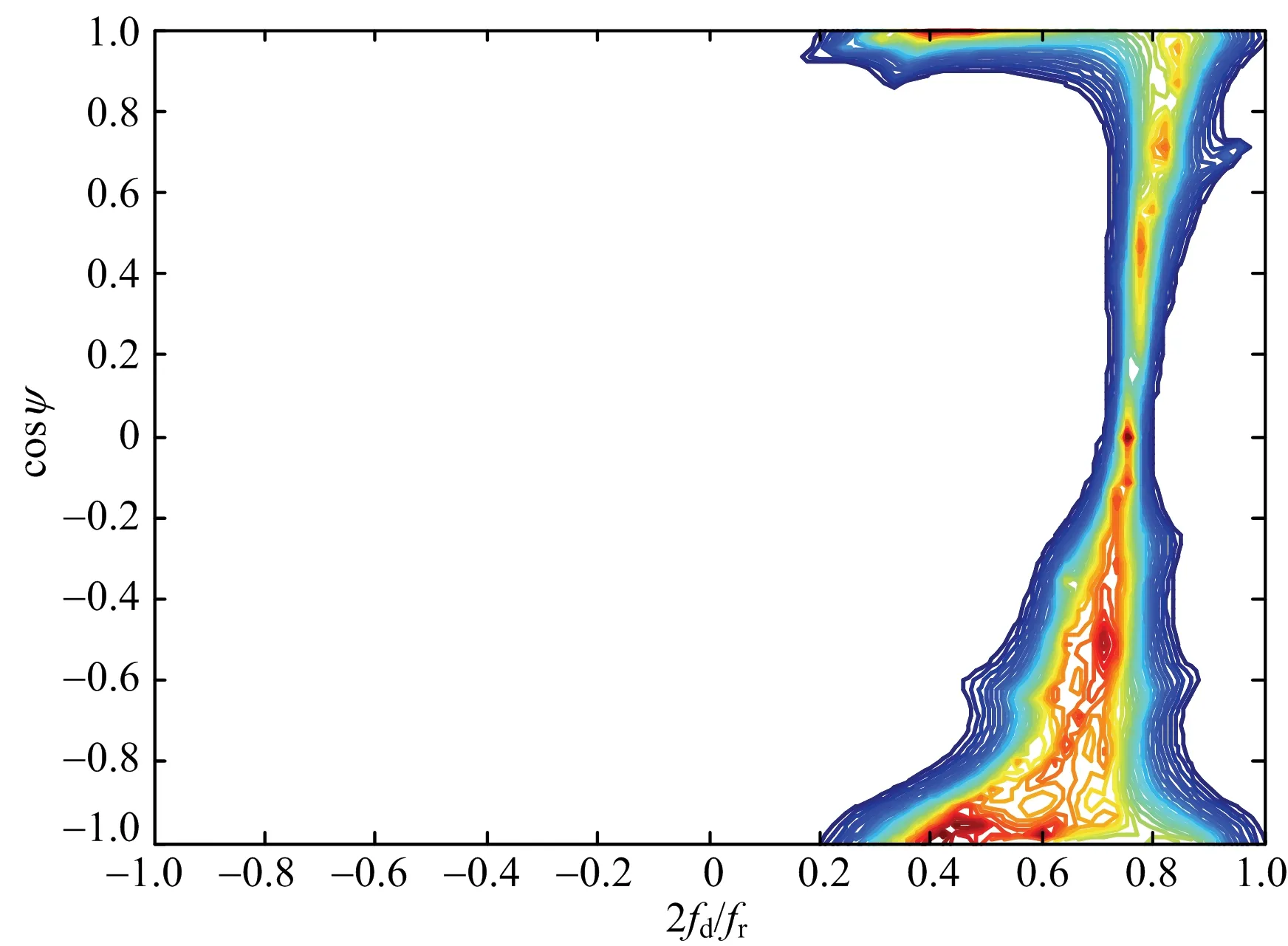
(a) 理論譜

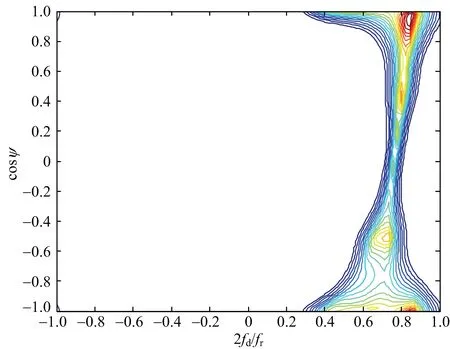
(b) 重構譜圖5 收發球心角5°的雜波功率譜

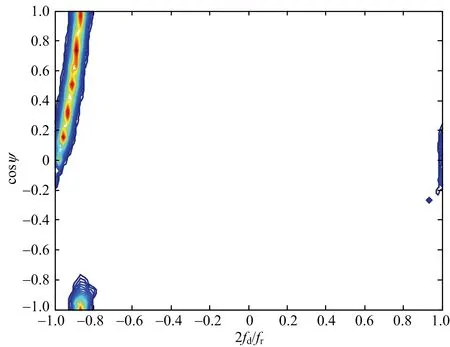
(a) 理論譜

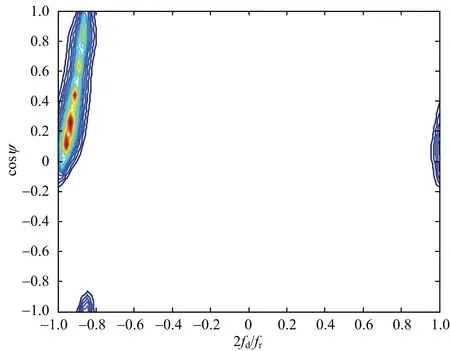
(b) 重構譜圖6 收發球心角10°的雜波功率譜

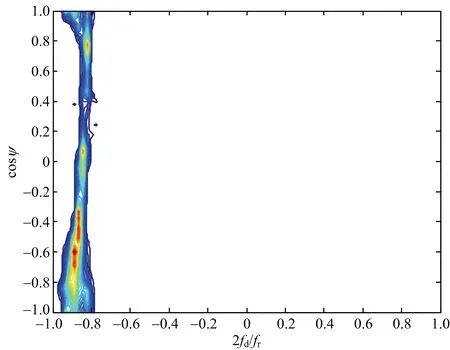
(a) 理論譜

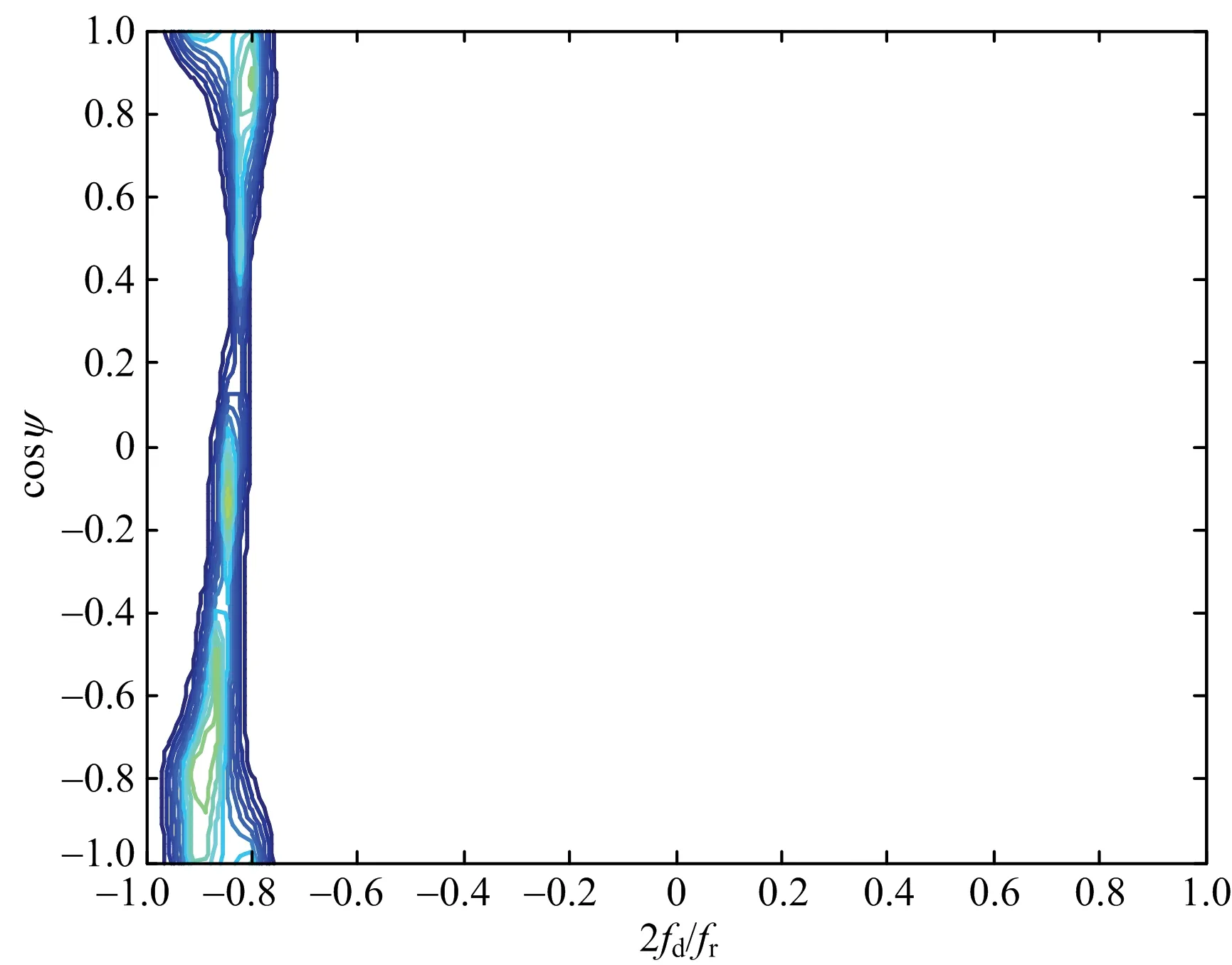
(b) 重構譜圖7 收發球心角15°的雜波功率譜

4.3 雜波抑制仿真

利用重構雜波協方差矩陣對不同收發球心角下的距離模糊雜波進行STAP處理，得到的改善因子三維圖如圖8所示。

取上述改善因子一個多普勒通道并與臨近單元取平均方法的抑制效果進行比較，仿真結果如圖9所示。

(b) 收發球心角10°

(c) 收發球心角15°圖8 改善因子三維圖

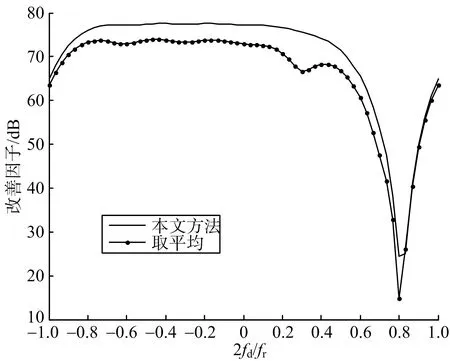
(a) 收發球心角5°

(b) 收發球心角10°

(c) 收發球心角15°圖9 改善因子對比圖

由圖9可知，在不同收發球心角下，使用本文方法進行補償后的雜波抑制效果明顯好于臨近單元取平均后的雜波抑制效果，其主雜波區的凹口更窄，多普勒展寬減小，改善了天空雙基地預警雷達雜波抑制效果和對慢速目標的檢測性能。這是由于在重構協方差矩陣時，將近程和遠程的模糊距離環雜波同時考慮在內，重構雜波協方差矩陣與理論值十分接近。采用臨近單元取平均方法時，由于雜波非平穩性的存在，使得雜波協方差矩陣估計不準，導致抑制性能下降。

5 結束語

本文在研究天空雙基地預警雷達雜波特性的基礎上，綜合考慮非平穩性和距離模糊問題，提出一種基于子孔徑平滑處理和重構雜波協方差矩陣的距離模糊非平穩雜波抑制方法。結果表明，該方法提高了天空雙基地預警雷達非平穩雜波抑制效果和對慢速目標的檢測能力。但在重構雜波協方差矩陣時，重構功率譜與理論功率譜在幅度上仍有所差異，這是本文方法的不足。