單頻網外輻射源雷達定位算法分析

(中國電子科學研究院，北京 100041)

0 引 言

外輻射源雷達是一種雙/多站構型的雷達系統，本身并不發射電磁波，通過被動接收第三方發射的電磁信號，對目標進行定位、跟蹤。相對于傳統雷達，外輻射源雷達具有優良的“四抗”性能[1-3]。

然而傳統外輻射源信號采用多頻網模式(各輻射站頻率不同)，頻率利用率低、功耗大，容易對其他網絡產生干擾并且覆蓋盲區大。而隨著數字信號和正交頻分復用技術的發展，單頻網模式應運而生。單頻網由多個處于同步狀態的無線電發射塔組成，這些發射塔采用相同的頻率，在同一時刻發射相同的電磁波，以完成對特定服務區的可靠覆蓋[4]。

單頻網外輻射源雷達是指輻射源采用單頻網輻射源的外輻射源雷達，屬于多基地雷達(多發射單/多接收雷達)的一種。其不僅兼有單頻網和傳統外輻射源雷達的優勢，而且相比于多頻網外輻射源雷達具有以下優點[5]：1)系統多采用多發單收模式并且各回波信號同時處理，相對于多頻網采用多發單收(分時處理)或單發多收的模式具有系統性能高、硬件成本低的優點；2)只有一個發射站，設備集中，系統維護簡單便捷；3)接收的數據集中于一個節點，處理集中，軟件成本低；4)各節點之間通信少，安全性更高(抗反輻射導彈能力強)，而多頻網數據分散于各個節點，聯合處理各節點之間需要頻繁通信，安全性能低。近年來，數字廣播電視信號逐步取代模擬信號，單頻網技術因具有頻率節約、頻譜利用率高等諸多優勢，更是得到廣泛應用。基于單頻網數字廣播電視信號的外輻射源探測也相應成為近年來的研究熱點。

然而，由于單頻網中所有發射站發射信號完全相同，在接收端能夠接收到所有發射站信號的回波，但是無法對每個發射站的回波進行區分，從而導致測量-發射站模糊[6-9]。即恒虛警檢測后能夠獲得距離-多普勒點跡，但是這些點跡來自哪一個發射站是未知的。如果不解決該模糊問題，直接進行目標關聯會出現海量虛警，后續的目標跟蹤無法實現。本文首先對測量-發射站關聯問題進行了建模，然后從目標定位算法選擇的角度出發，分析了不同定位方法的定位精度以及對測量-發射站關聯問題的影響，并通過三發單收的外輻射源定位模型進行了仿真分析。

1 測量-發射站關聯

測量-發射站的關聯是單頻網外輻射源雷達的一個關鍵問題，主要是由同頻發射站對同一目標的照射引起的，如圖1所示。

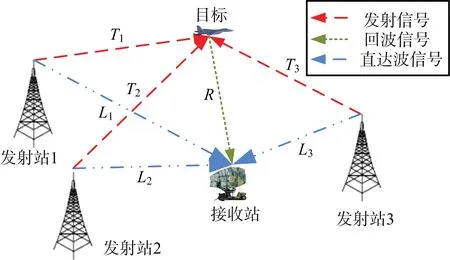
圖1 單頻網外輻射源雷達探測系統

假設發射站位置為TXs，接收站位置為RX，目標位置xt，目標速度為vt，則目標的距離和多普勒頻率為

(1)

考慮噪聲的影響，假設噪聲是高斯加性白噪聲nr～N(0,σr),nf～N(0,σf)，則

(2)

式中，c表示電磁波在空氣中的傳播速度。如果目標狀態已知，則測量的條件概率可表示為

(3)

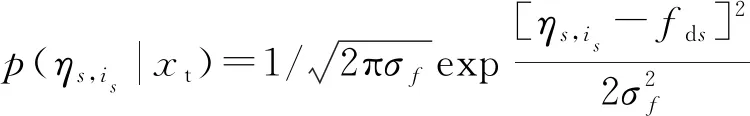
(4)

在實際場景中，并不是所有的發射站都能夠探測到目標，則S維測量的似然概率可表示為

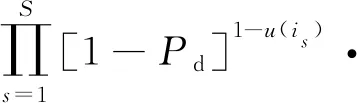
[Pdp(ωs,is|xt)]u(is)

(5)

式中，u(is)是一個指示函數，表征第is個測量是否屬于目標，其定義如下：

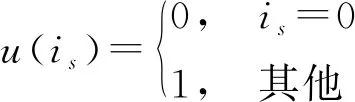
(6)

當所有測量均為虛警時，似然概率可表示為

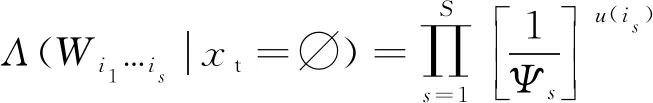
(7)

式中，Ψs表示第s個發射站觀測區域的體積。這樣，S維測量-發射站關聯的代價函數可表示為

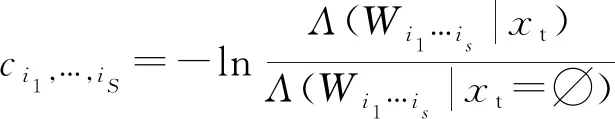
(8)

但是，目標xt的狀態是未知的，其可以用下式的似然估計代替：

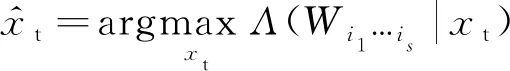
(9)

假設一個測量最多與一個目標關聯，一個測量最多與一個發射站關聯，同一個目標同一發射站最多有一個測量，則目標的測量-發射站的正確關聯可通過下式獲得：

(10)

式中，

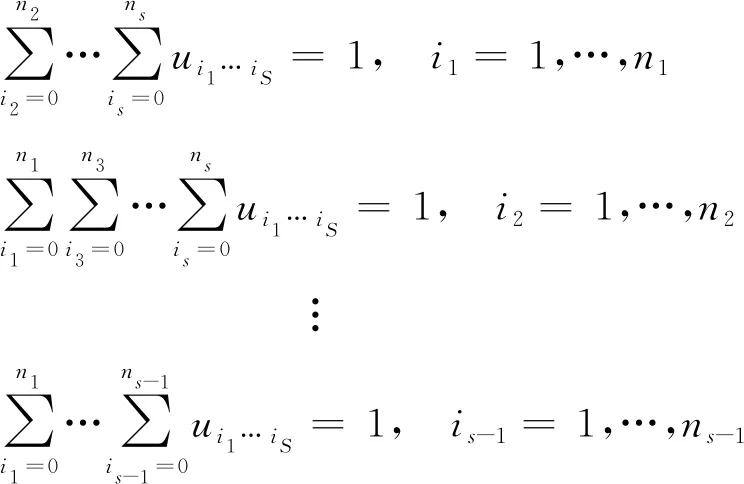
(11)

因為每個測量值的發射站來源是未知的，其可能來自于S個發射站中的任何一個，因而在利用這些測量時必須假設每個測量來自于所有的發射站。這樣測量的數目變為了原來的S倍。假設有M個測量，則每個發射站對應的測量會有M+1個(需要考慮某發射站漏檢的情況)，如圖2所示。

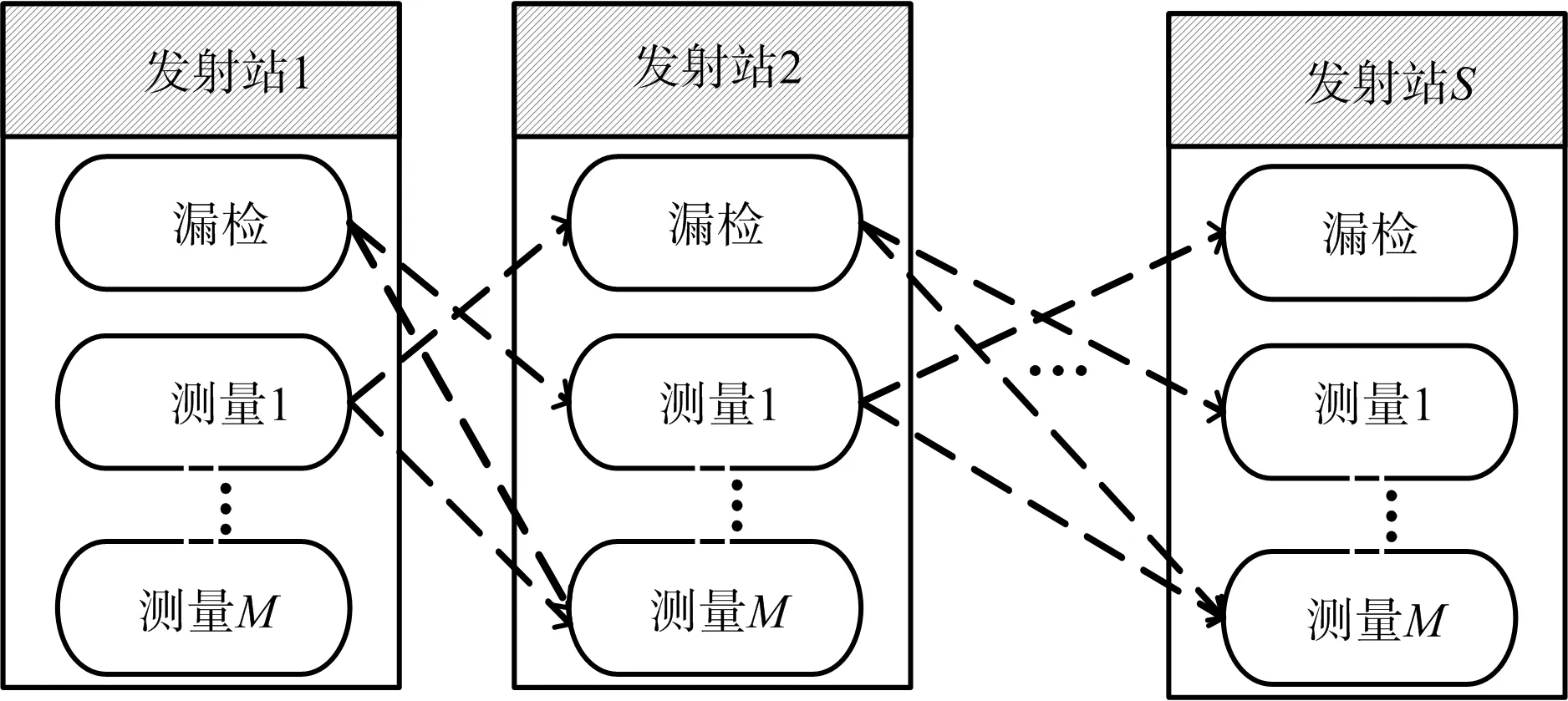
圖2 測量-發射站關聯示意圖

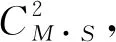
圖3 關聯問題示意圖

假設有S個發射站、1個接收站、N個目標和M個測量，則需要關聯的事件的數目為

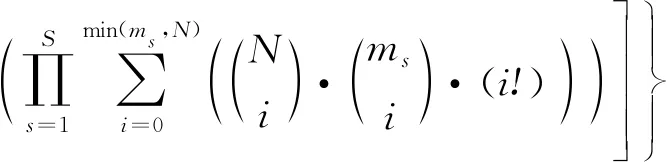
(12)

式中，ms表示與發射站s關聯的測量數目。假設有3個目標、5個發射站、12個測量，則需要考慮的關聯的數目高達353 767 425。已經被證明[10]，當發現概率小于1、發射站數目S≥3時，該關聯問題是一個NP的問題。

2 基于TOA的定位方法原理

2.1 三維TOA定位方法

TOA定位采用同一目標的多個時延測量τs構造多個空間曲面求交點即可得到目標的位置[11]。

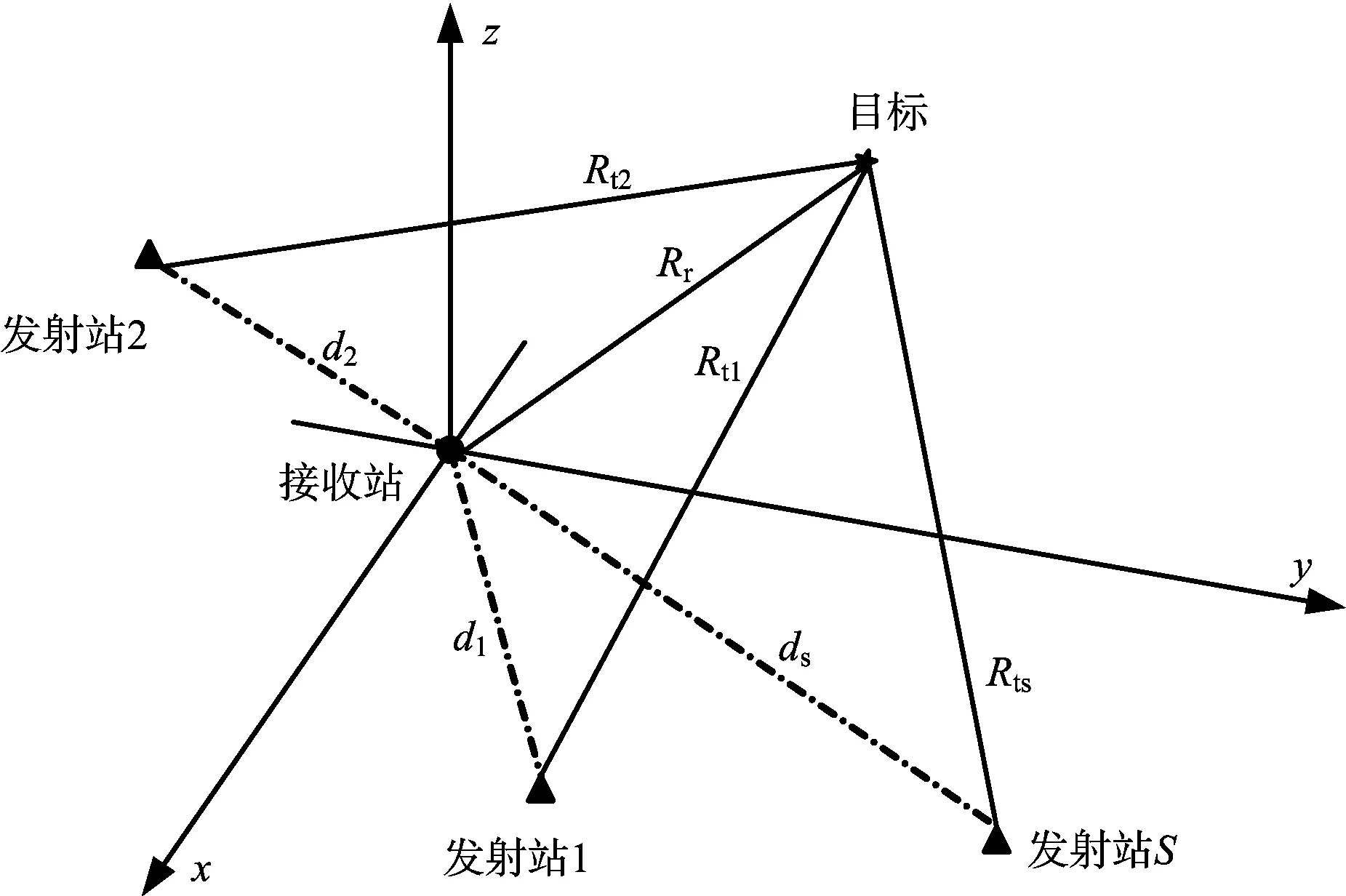
圖4 TOA定位示意圖

如圖4所示，為不失一般性，假設接收站位置為坐標原點RX(0,0,0)T，第s個發射站位置TXs(xts,yts,zts)T，目標位置xt(x,y,z)T。目標與接收站的距離Rr可表示為

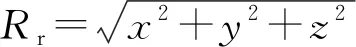
(13)

目標與發射站之間的距離可表示為

(14)

同樣，第s個發射站與接收站之間基線的距離可表示為

(15)

通過時延信息可以獲得目標與發射站和接收站的距離和信息：

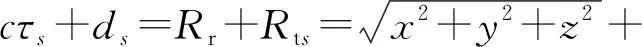
(16)

則上式變形可得

(17)

兩邊平方可得

(18)

令

(19)

則

Qxt=P+rRr

(20)

式中，r表示S個發射站-接收站的距離和信息向量，r=[R1,R2,…,RS]T。如果Rr已知，目標的最小均方誤差解可表示為

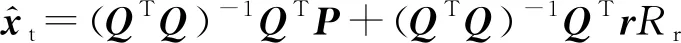
(21)

假設

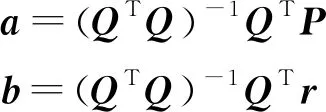
(22)

則有

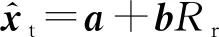
(23)

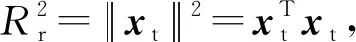
(24)

方程的解為

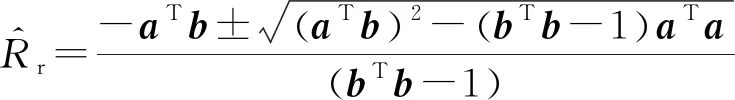
(25)

2.2 估計目標高度的二維TOA定位方法

假設目標位置為xt(x,y,H)，其中H表示根據目標的飛行高度范圍估計的目標高度，則目標與接收站的距離為

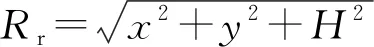
(26)

目標與發射站之間的距離可表示為

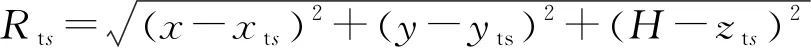
(27)

通過時延信息可以獲得目標與發射站和接收站的距離和信息：

(28)

則可得

(29)

兩邊平方可得

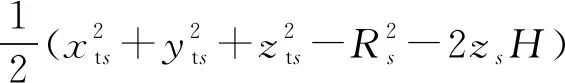
(30)

令

(31)

則

Qxt=P+rRr

(32)

如果Rr已知，目標的最小均方誤差解可表示為

x′t=[x,y]T=(QTQ)-1QTP+(QTQ)-1QTrRr

(33)

假設

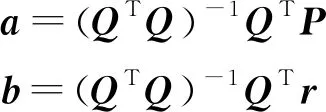
(34)

則有

x′t=a+bRr

(35)

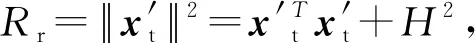
(36)

方程的解為

(37)

2.3 定位精度分析

同一目標經過不同發射站照射可以得到多個距離和測量，根據多個距離和測量信息對應的發射站-目標-接收站空間關系可以得到目標的空間位置。距離和測量公式兩邊求微分可得

dRi=(ci1+cr1)dx+(ci2+cr2)dy+kzi+

kti+kr,i=1,2,…,S

(38)

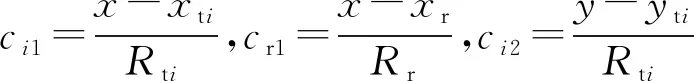
kti=-(ci1+cr1)dxti-(ci2+cr2)dyti-

(ci3+cr3)dzti

kr=-(ci1+cr1)dxr-(ci2+cr2)dyr-

(ci3+cr3)dzr

kzi=(ci3+cr3)dH

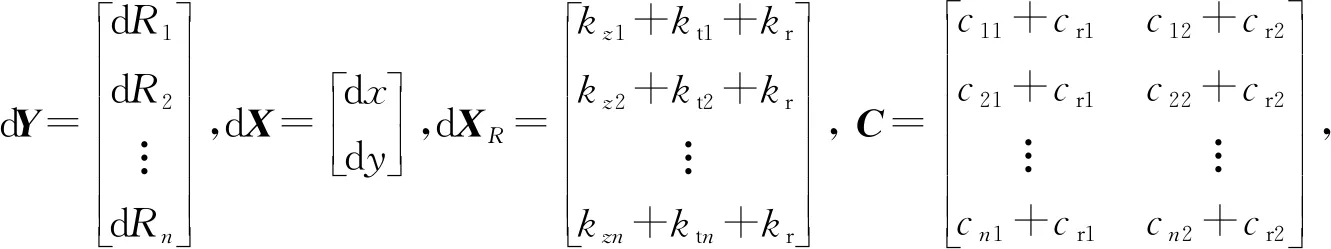
dY=CdX+dXR

(39)

目標位置誤差矢量為

dX=(CTC)-1CT(dY-dXR)

(40)

假設不同發射站得到距離和的測量誤差不相關，站址誤差不變，則定位誤差協方差為

P=E[dXdXT]=

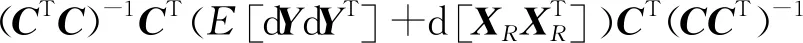
(41)

式中，

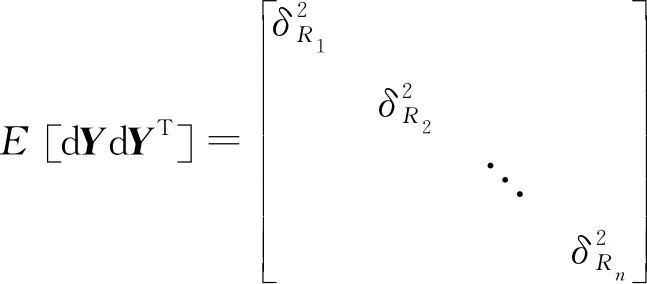
(42)

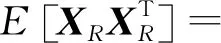
(43)

式中，δRi表示第i個發射站與接收站的距離和的標準差，δs表示站址誤差，δH表示目標估計高度與真實高度偏差的標準差。則基于TOA信息的定位精度表示為

(44)

3 仿真實驗分析

仿真條件：接收站坐標(30,40,0.1)km，發射站1坐標(-40,30,0.1)km，發射站2坐標(0,0,0.2)km，發射站3坐標(50,0,0.1)km，距離和測量誤差30 m，站址誤差10 m，目標位置在如圖5所示軌跡上，飛行高度7～11 km隨機選取。

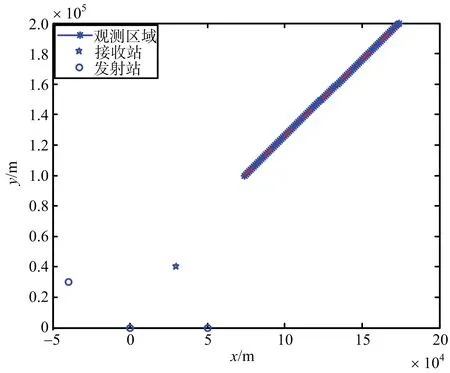
圖5 仿真場景

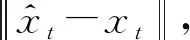
如圖6(a)和圖6(b)所示，在雙基距離較小時，三維定位算法在二維平面的定位精度要高于二維定位方法的定位精度，當雙基距離較大時二維定位算法的定位精度較高。在圖6(c)和圖6(d)中可以發現，三維定位算法在高度方向的定位精度隨雙基距離增加衰減較為嚴重，當雙基距離超過350 km時，高度方向的定位誤差甚至大于10 km，而根據目標的實際情況估計的目標高度誤差較為穩定。綜合圖6可知，當目標距離較近時，三維定位方法的定位精度較高；當目標距離較遠時，三維定位方法的高度定位誤差很大，導致目標的定位精度降低。而單頻網外輻射源雷達屬于預警探測雷達的一種，主要針對遠距離目標的探測和監視，因而二維定位方法相對三維定位方法更加適用。

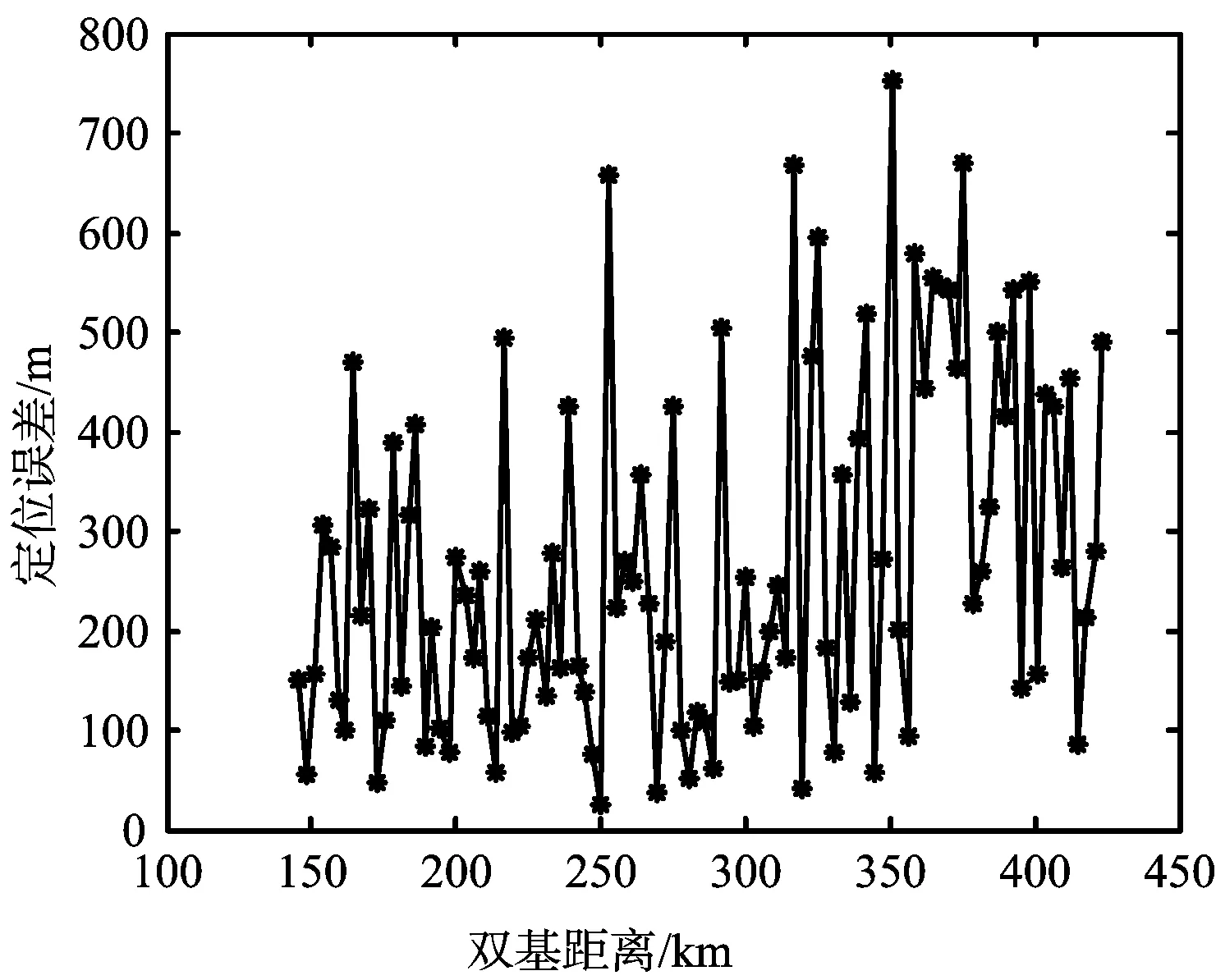
(a) 三維定位方法二維定位誤差

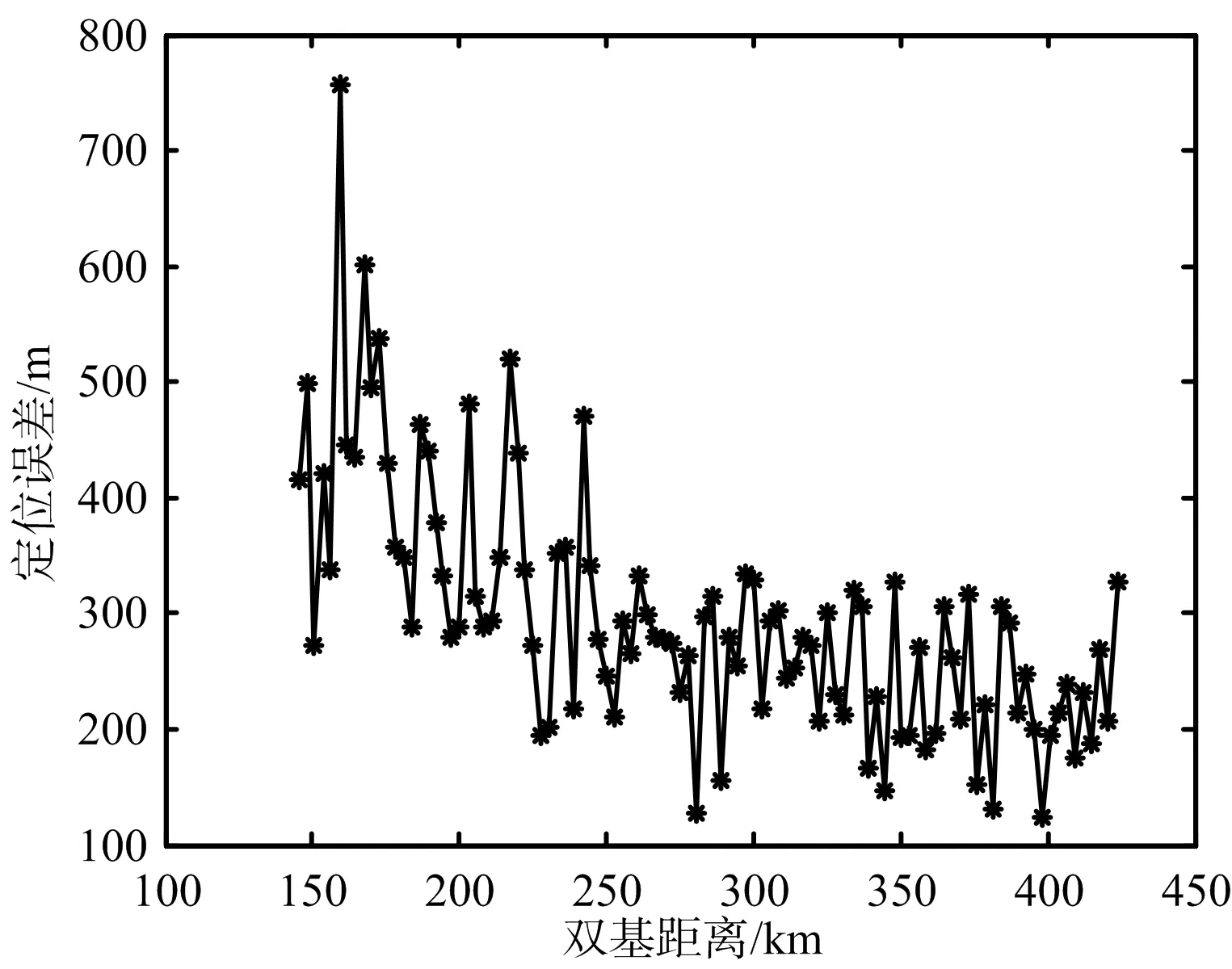
(b) 二維定位方法二維定位誤差

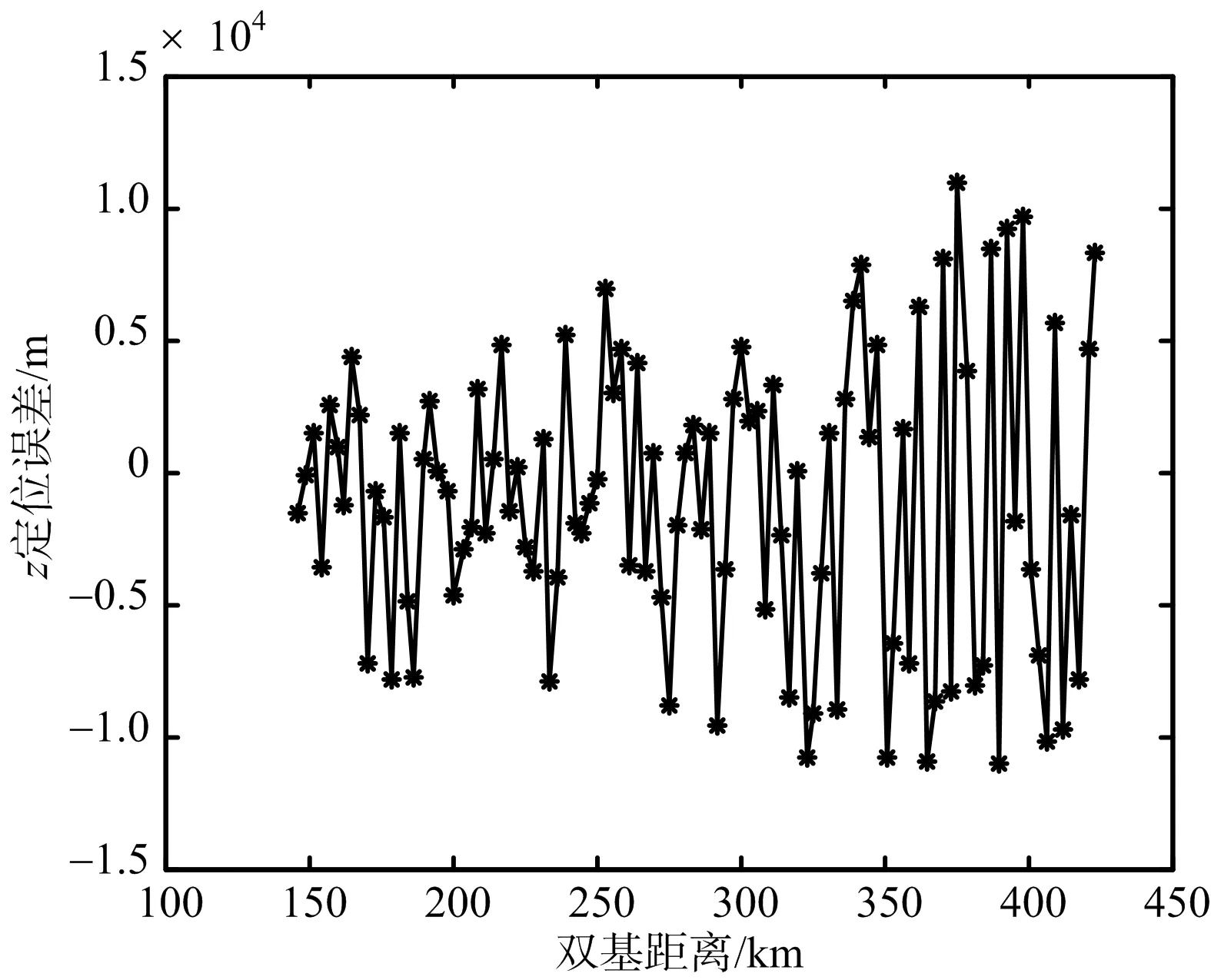
(c) 三維定位方法高度定位誤差

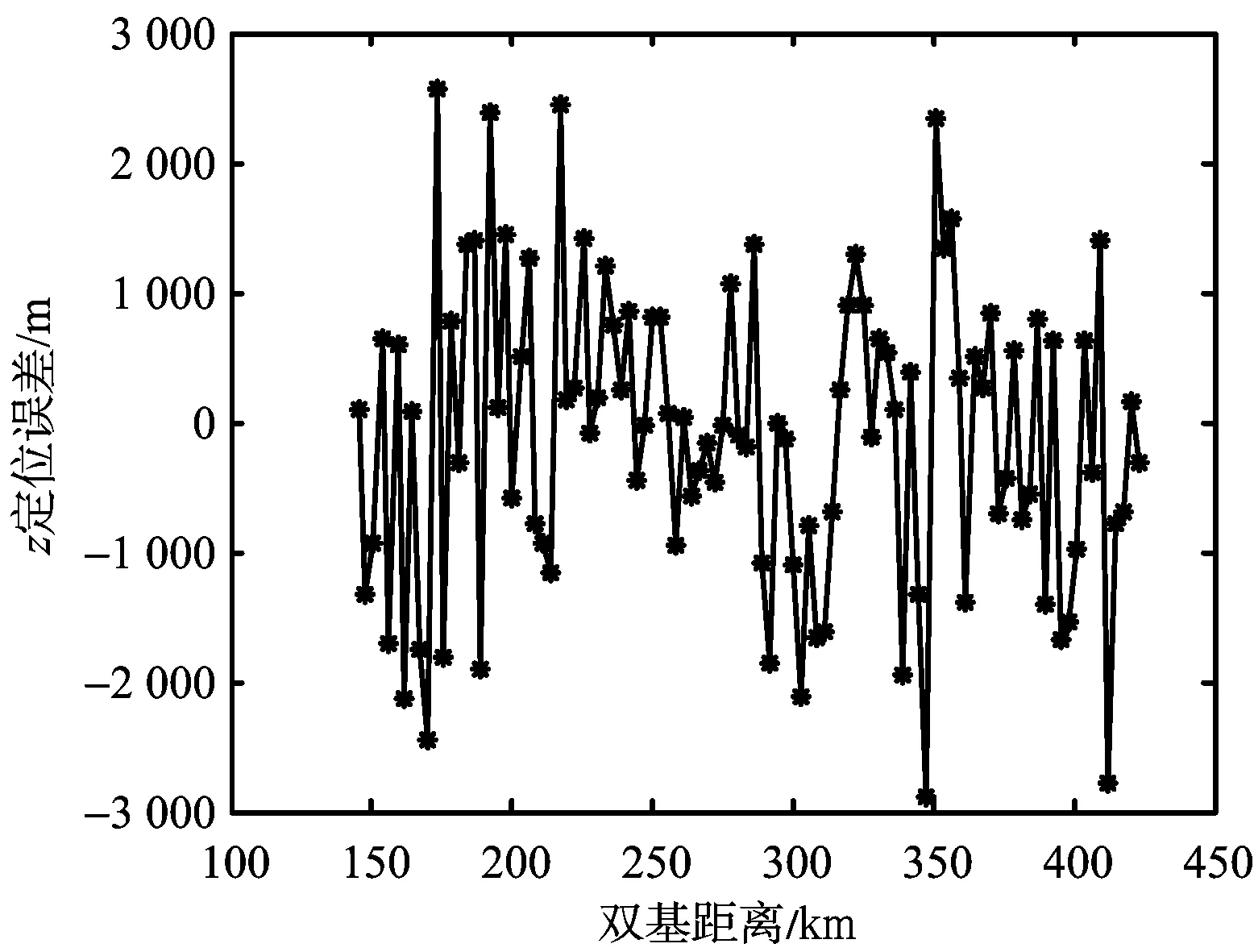
(d) 目標高度估計誤差圖6 定位誤差分析

而由之前的工作[13]可知，估計目標的距離和誤差越大，正確關聯的概率越小，在單頻網外輻射源雷達定位方法選擇時必須確保估計目標的估計誤差盡量的小以保證較高的關聯概率。圖7表示目標估計的距離和誤差。

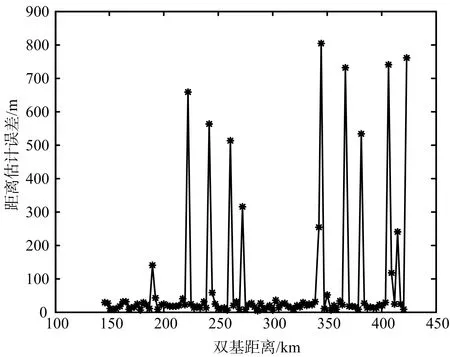
(a) 三維定位方法目標距離和誤差

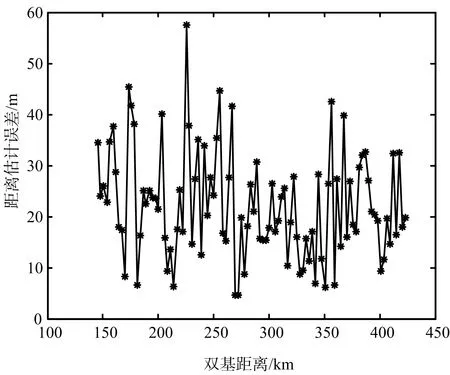
(b) 二維定位方法目標距離和誤差圖7 距離和誤差分析

目標距離和誤差的測量值一般小于一個距離單元的距離(對于10 MHz采樣率的數字電視信號，一個距離單元雙基30 m)，因而可以將距離和的測量值作為目標距離和的真值。當目標距離和的估計值與測量值相差較小時，可以完成正確關聯。由圖7(a)和圖7(b)可知，三維定位方法獲得的目標距離和誤差存在很多奇點會導致關聯概率降低，錯誤關聯數目上升，而估計目標高度的二維定位方法獲得的距離和誤差較小較穩定，能夠更好地保證測量-發射站關聯質量。

4 結束語

本文建立了單頻網外輻射源雷達測量-發射站關聯模型，分析了測量-發射站關聯問題對后續數據處理的影響。然后從目標定位算法選擇的角度出發，分析了不同定位方法的定位精度以及對測量-發射站關聯問題的影響，并通過一個三發單收的單頻網外輻射源雷達定位模型進行了仿真驗證。綜合目標的二維定位精度和目標距離和估計誤差可以發現，估計目標高度的二維定位方法更適合單頻網外輻射源雷達的定位和測量-發射站解模糊。