基于速度修正的固壁邊界處理方法

朱曉臨，陳 薇

基于速度修正的固壁邊界處理方法

朱曉臨，陳 薇

(合肥工業大學數學學院，安徽 合肥 230009)

固壁邊界處理方法的研究一直是流體模擬中的難點問題，常見的固壁邊界處理方法有邊界力法和虛粒子法。邊界力法通過對靠近邊界的流體粒子施加作用力防止其穿透邊界，但模型參數較多，力的大小難以調控，且在計算中會產生邊界截斷誤差問題；虛粒子法通過在邊界外生成虛粒子解決了邊界截斷誤差問題，但在處理復雜邊界問題時，由于外部的虛粒子的生成較困難，且分布不均，計算精度受到影響，出現粒子飛散的情況。針對2種方法存在的問題，提出一種基于速度修正的固壁邊界處理方法，無需求解邊界力或在邊界外生成虛粒子，直接利用動量方程和計算速度耗損量求出流體粒子碰到邊界后的反彈速度，大大降低了處理邊界的復雜程度，也克服了2種方法在邊界拐角處粒子不均勻采樣而導致的算法不穩定的問題。模擬仿真驗證了該方法在穩定性、計算效率方面均較傳統邊界力法和虛粒子法更好；隨著粒子數的增加，該方法耗時更少、計算效率更高，對復雜場景的模擬效果更好。

流體模擬；固壁邊界；邊界力法；虛粒子法；速度修正

光滑粒子流體動力學(smooth particle hydrodynamics, SPH)方法是流體模擬，尤其是液體模擬的主要方法。流體模擬的固壁邊界處理方法主要包括邊界力法和虛粒子法2種。

邊界力法應用一層邊界粒子來表示固壁邊界，通過該層邊界粒子對鄰近邊界的流體粒子施加作用力，防止流體粒子穿透固壁邊界。其關鍵是壁面作用力的施加模型。

1994年，MONAGHAN[1]最先提出通過施加邊界力的方式進行固壁邊界處理，并提出蘭納-瓊斯(Lennard-Jones，L-J)勢函數作為作用力的施加模型，但該模型中存在許多未知參數，需要根據具體問題進行調整，調整不當可能會導致流體粒子穿透邊界或粒子飛亂等問題。2004年，MüLLER等[2]基于L-J勢函數實現了在微可壓縮情況下，將SPH方法用于模擬流體與可變形固體的相互作用，并且在作用力較大時，流體粒子不會穿透固體邊界，但需要更小的時間步長來確保模擬的穩定性。2007年，HARADA等[3]針對邊界粒子不足的問題，提出一種邊界粒子密度權重函數，將邊界粒子的密度加入到流體密度的計算中，從而減小了因邊界粒子的不足造成的計算誤差。2009年，BECKER等[4]以直接力的方法處理固壁邊界，同時采用預測-校正技術計算粒子的速度和位置。上述方法僅適合規則固體邊界的情況，且在計算鄰近邊界粒子的屬性時由于邊界外測粒子的缺失導致計算會產生截斷誤差。

2009年，MONAGHAN和KAJTAR[5]采用一種簡化的邊界力計算公式克服了L-J勢函數方法計算邊界力參數較多的不足，但力的大小和作用范圍仍難以控制。2012年，LIU等[6]提出了一種新型邊界力模型，并將邊界粒子與虛粒子結合施加邊界條件，但若單獨使用一層邊界粒子表示固壁邊界，仍會出現流體粒子穿透邊界的問題。邊界力法可以方便地表征復雜的邊界，且實現方法相對簡單，易于編程。然而，主要缺點為邊界力的范圍和強度難以控制，若邊界力太大，則會導致邊界附近粒子屬性的數值計算波動較大造成粒子飛亂；反之則將導致流體粒子穿透邊界。

虛粒子法應用多層虛粒子表征固壁邊界，通過插值或鏡像方式將流體粒子的部分屬性(質量、密度、壓強等)賦予虛粒子，虛粒子與流體粒子通過流體力學控制方程相互作用。虛粒子法的關鍵是其屬性值的獲取及與流體粒子的相互作用。

1996年，RANDLES和LIBERSKY[7]提出通過鏡像方式生成虛粒子進行邊界處理，如果流體粒子到邊界的距離小于其支持域半徑，那么在固壁外就會自動生成鏡像虛粒子，流體粒子和鏡像虛粒子的速度大小相等但方向相反，其他物理量相同。1997年，MORRIS和MONAGHAN[8]使用插值虛粒子法模擬SPH流體與固壁邊界的相互作用。2002年，LIU等[9]提出在固壁邊界處布置2種虛粒子，第一種是固定在邊界上，且對靠近邊界的流體粒子施加一個排斥力，從而防止流體粒子穿透邊界；第二種是由鄰近邊界的流體粒子對稱產生的，并賦予其相應物理量，從而使得邊界附近的流體粒子在進行積分計算時不會產生截斷誤差。2006年，HU和ADAMS[10]使用鏡像虛粒子法模擬流體在規則固體邊界條件下的運動，虛粒子設置在流體粒子作用域與邊界重疊的部分，并且虛粒子與流體粒子具有相同的密度、質量、壓力和黏度，將虛粒子看作是流體粒子進行處理。上述方法只適用于規則固壁直邊界，對于復雜邊界情況，虛粒子的生成過于復雜，計算量較大。

2012年，SCHECHTER和BRIDSON[11]提出了一種新鏡像粒子法來模擬流體的自由表面和進行邊界處理。該方法在液體和固體之間以及液體和空氣之間產生鏡像粒子，并使用液體粒子通過插值運算推導出鏡像粒子的屬性值。該方法解決了存在于流體自由表面附近的非自然張力視覺形變問題和在固壁邊界處無法真實模擬的流體的黏附現象。2015年，劉虎等[12]提出了應用一系列的虛粒子來表征固壁邊界的處理方法，當求解方程式時，讓虛粒子具有流體粒子的部分屬性(密度、質量、壓力等)，求解其連續方程和狀態方程，并將邊界問題耦合到方程的求解過程中，無需提出顯式的邊界條件。該方法的優點是無需對邊界進行特殊的處理，缺點是通過求解連續方程和狀態方程得到的虛擬粒子的壓力，與真實壓力之間存在誤差，導致模擬的不穩定，出現粒子飛散的情況。雖然虛粒子法的守恒性較好，精度也較高，但在生成自由表面的虛粒子時過于復雜，計算時間大大增加，固壁邊界形狀復雜時更加如此。

總體而言，邊界力法適合處理復雜的固體邊界，然而模型的參數較多，力的大小難以調控，并且在計算過程中會產生邊界截斷誤差問題；虛粒子法能夠很好地解決邊界截斷誤差，但在處理復雜邊界問題時，邊界外部的虛粒子的生成較困難，計算精度和穩定性難以保證，會出現粒子飛亂甚至程序運行崩潰的情況。

針對上述問題，本文提出一種基于速度修正的固壁邊界處理方法，無需在邊界外生成虛粒子或求解邊界力，直接利用動量方程和計算速度耗損量求出流體粒子遇到邊界后的反彈速度，大大降低了處理邊界的復雜程度，也克服了虛粒子法和邊界力法在拐角處粒子不均勻采樣而導致的算法不穩定的問題。模擬仿真驗證了本文方法在穩定性、計算效率方面均比傳統方法更好；隨著粒子數的增加，本文方法的耗時增長慢于傳統方法，計算效率高的優勢更明顯；對復雜場景的模擬效果更好。

1 SPH方法簡介

1.1 SPH基本公式

在SPH方法中，函數()定義為

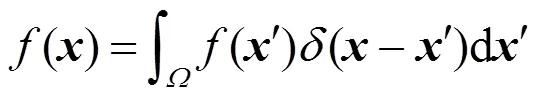
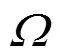
其中，為光滑函數的影響和支持范圍即光滑長度；則稱為光滑核函數(smoothing kernel function)或光滑函數(smoothing function)，簡稱為核函數(kernel)。

本文采用三次樣條的核函數

其中，=/；α為函數在維空間中的歸一化系數，其在一維、二維和三維空間中的取值分別為1/，15/(7π2)，3/(2π3)。

通過將式(3)離散化，用光滑函數的支持域內所有粒子疊加求和的形式表示任一點處的粒子近似式為

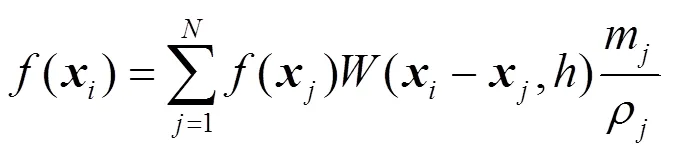
其中，為粒子的支持域內的粒子總數；m，，分別為支持域范圍內粒子的質量、密度和位置；(–,)為粒子對粒子產生影響的光滑函數，且該函數與光滑長度有關。

1.2 控制方程

本文用到的是拉格朗日形式的Navier-Stokes方程(簡稱N-S方程)

本文采用SPH方法的計算過程流程如圖1所示。

圖1 SPH方法的流程圖

使用SPH方法求解N-S方程，對于任一粒子，其密度為

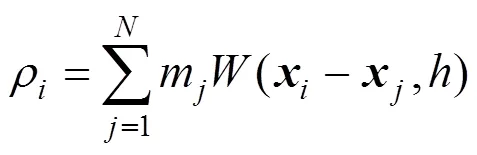
求得粒子密度后，還需要計算粒子壓強，進而求得粒子的壓力。

利用泰特方程求壓強，即

其中，為常數，一般取=7；為參數，用于限制密度的最大改變量；0為參照密度。

SPH方法中求解粒子所受的壓力和黏性力的表達式分別為

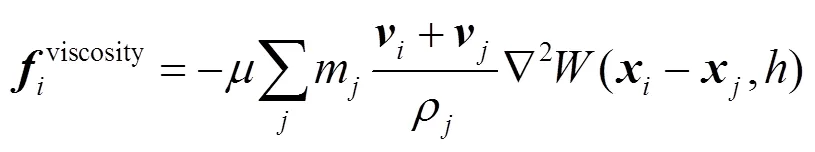
流體粒子的速度、位置等信息是根據其所受合力計算所得，利用式(10)和式(11)，將N-S方程中的動量守恒方程式(7)轉化為

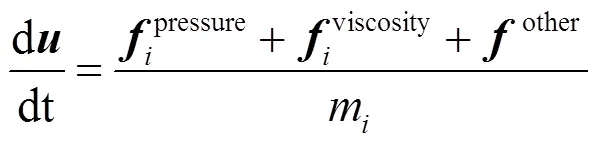
2 基于速度修正的固壁邊界處理方法

文獻[1]最早提出應用邊界力的方式施加流固邊界條件，并提出一種基于距離的L-J勢函數的方法施加作用力

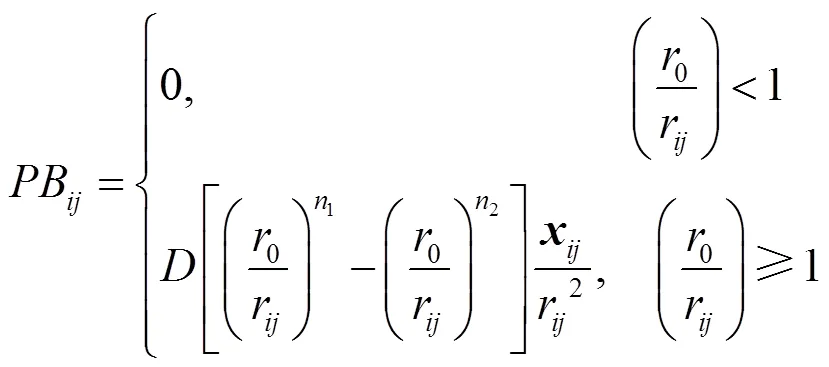
其中，系數1一般取12，2一般取4；的取值一般為流體最大速度的平方量級；0為光滑核半徑；r為流體粒子到固體邊界上位置點的距離；為流體粒子位置到固體邊界上位置點之間的向量。

文獻[7]在處理直壁邊界問題時，能夠很好地解決邊界截斷誤差，但在處理圓弧表面、傾斜壁面等邊界問題時，邊界外部的鏡像粒子的生成較困難，并且鏡像粒子分布不均，計算精度也會受影響，出現粒子躍出甚至程序崩潰的情況。

目前，已有的邊界處理方法都很難兼顧計算精度、邊界復雜度以及計算效率。本文提出一種新的基于速度修正的固壁邊界處理方法：先在邊界上設置一個阻尼區，當流體粒子運動到阻尼區內時，且流體粒子速度與邊界法向夾角大于π/2時，將該區域分為4個小區域，并分別對流體速度作不同處理：將流體粒子速度從，坐標系轉化為，坐標系表示(其中，分別為邊界的法向與切向)；然后用流體粒子與相關的邊界粒子的相對位置計算速度耗損量；之后將不同區域的流體粒子反彈到相應區域；最后將處理后的流體粒子速度轉回，坐標系。具體步驟如下：

(1) 添加阻尼區。以邊界斜坡為例(圖2)：在斜坡邊界(黑色線條)上方添加阻尼區邊界(藍色線條)，阻尼區的寬度為，其數值與粒子的支持域長度(即核函數的光滑長度)相同。

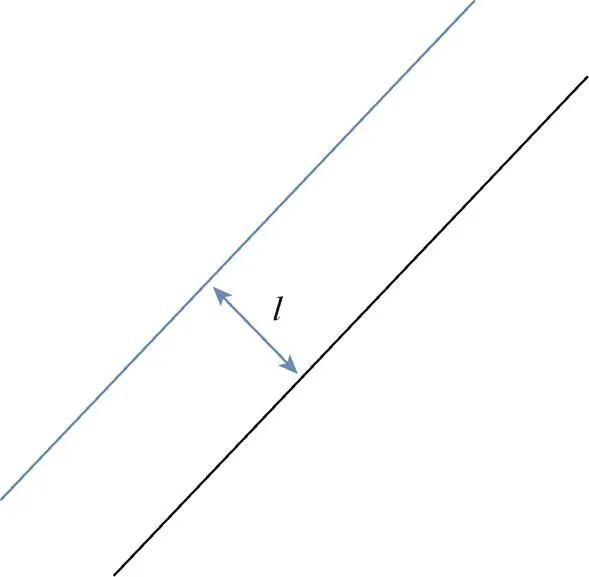
圖2 邊界阻尼區示意圖

(2) 流體粒子到邊界的距離。在邊界上等距分布粒子，邊界粒子間距與初始流體粒子間距有關。流體粒子到邊界的距離定義為：流體粒子到邊界粒子的2個最短距離的平均值作為該流體粒子到邊界的距離，如圖3所示。

圖3 流體粒子到邊界粒子的距離

(3) 劃分區域。當流體粒子在阻尼區內，且其速度方向與邊界法向夾角大于π/2時，將該區域分為①、②、③、④4個小區域，如圖4所示，其中，①~④為第1~4個小區域。

依本文方法，區域①中的粒子將反彈到區域⑧中；區域②中的粒子反彈到區域⑦中；區域③的粒子反彈到區域⑥中；區域④的粒子反彈到區域⑤中。在流體粒子碰到邊界反彈的過程中，其反彈速度會受到周圍流體粒子的影響，故需要計算速度的耗損量。

(4) 計算速度耗損量。在流體粒子周邊的邊界粒子數為，記為1,2,···,，如圖5所示。

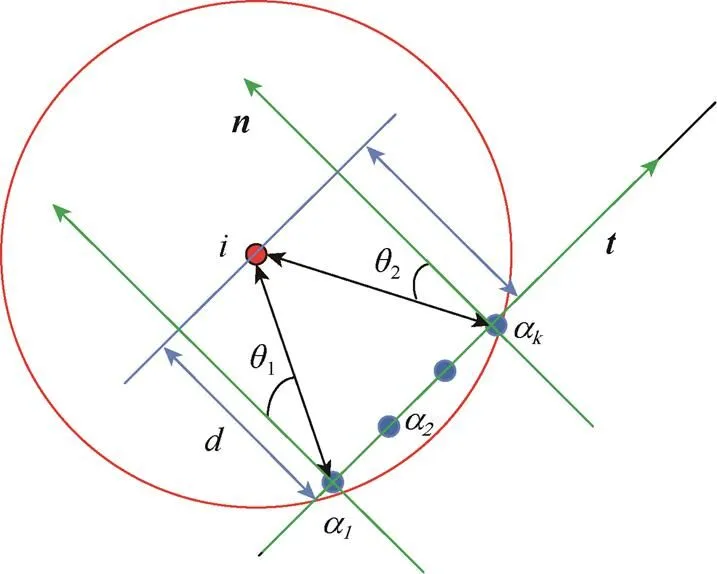
圖5 流體粒子與邊界粒子的夾角

由圖5得

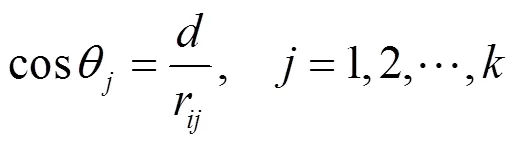
其中，為流體粒子到邊界的距離(式(14))，r為粒子到粒子α的距離(=1,2,···)。

計算粒子速度耗損量為

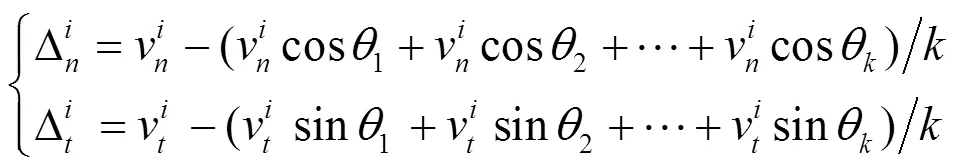
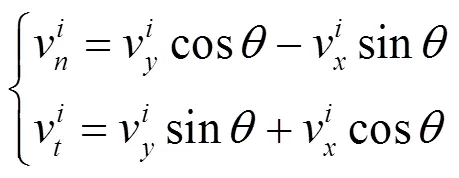
當粒子到達邊界時會發生反彈，各種復雜邊界均可用類似的方法進行處理。

將本文方法與傳統邊界力法和虛粒子法進行對比，可以發現：①在穩定性方面，邊界力法是通過基于距離的L-J函數來計算鄰近邊界的流體粒子受到的排斥力，當流體粒子運動到拐角處時，因受到來自相同距離邊界粒子施加的力的影響導致粒子的反彈速度的計算不穩定；虛粒子法在處理復雜邊界問題時，邊界外部的鏡像虛粒子的生成較困難，且分布不均勻，計算精度受影響。本文方法可對邊界的形狀做檢測，通過計算速度耗損量對速度進行修正，可以更好地控制粒子在拐角處運動的穩定性，克服了傳統方法在邊界拐角處粒子不均勻采樣而導致的算法不穩定的問題。②在計算效率方面，與邊界力法相比，本文方法無需使用較多參數且通過較復雜的邊界力模型來計算力，而是直接對速度進行修正，通過計算速度耗損量求出流體粒子遇到邊界后的反彈速度，減小了計算量；與虛粒子法相比，本文方法無需在邊界外部生成虛粒子，降低了處理邊界的復雜程度，尤其在處理復雜邊界問題時，虛粒子的生成較困難，且在計算流體粒子的速度及位置信息時，虛粒子也參與其中，使得計算量大大增加。因此，本文方法在穩定性和計算效率方面均要優于傳統的邊界力法和虛粒子法。

3 實 驗

3.1 二維潰壩模擬

以二維潰壩實驗模擬斜坡邊界和弧形邊界場景，驗證本文方法在穩定性和計算效率方面的有效性。相關參數：流體粒子的初始密度為1 000 kg/m3，粒子初始間距為0.002 92 m，時間步長為10×10–3s，粒子的支持域長度=0.006 m。

(a) 邊界力法(b) 虛粒子法(c) 本文方法

由圖6可知，圖6(a)為邊界力法，穩定性略差，粒子撞到邊界后，上爬升過程中出現輕微的粒子飛散現象；圖6(b)為虛粒子法，穩定性差，粒子撞到邊界后，上爬升過程中粒子飛散情況明顯；圖6(c)為本文方法，在粒子撞到右側邊界后，爬升時的穩定性好，沒有出現明顯的粒子飛散情況，與實際中水撞到固壁邊界后爬升的效果更為接近。

上述3種方法模擬實驗進行流體粒子總數分別為2 500個、5 000個和7 500個粒子，每組實驗進行5次取運行到2 000幀時的平均值作為運行時間，模擬二維潰壩斜坡邊界運行時間的結果見表1。

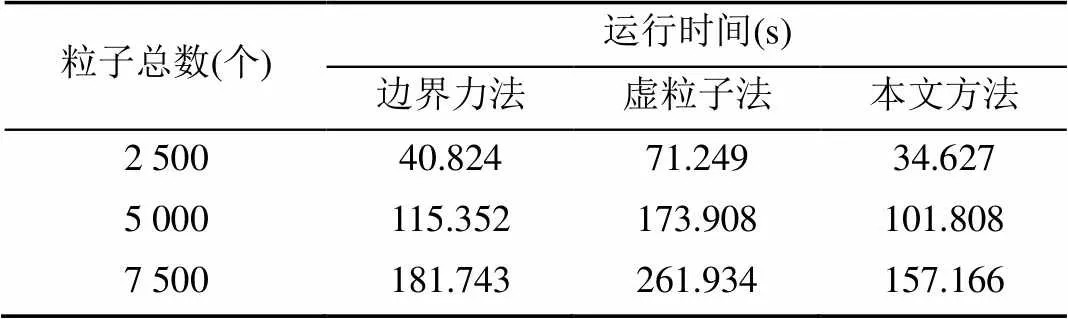
表1 3種方法模擬二維潰壩斜坡邊界的運行時間

由表1和圖7可以看出，本文方法明顯比傳統的邊界力法和虛粒子法的計算效率高，并且隨著粒子數的增加，耗時增長也比其他2種方法慢，計算效率高的優勢更明顯。

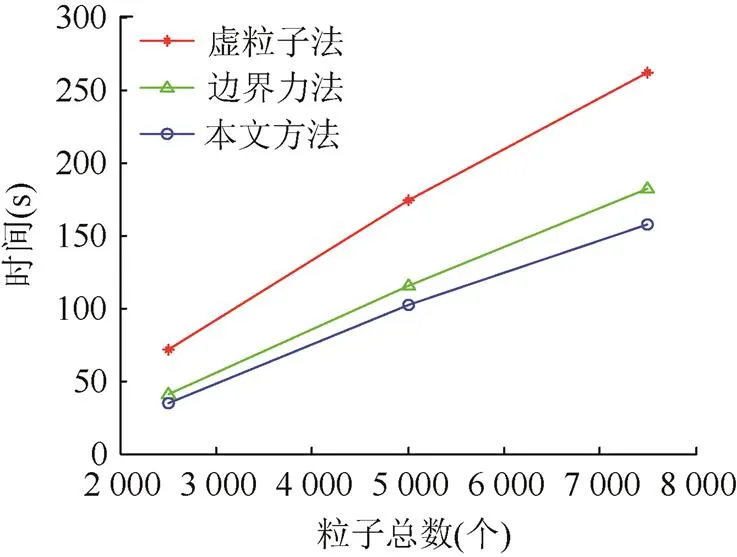
圖7 隨著粒子數的增加，邊界力法、虛粒子法和本文方法耗時增長對比

同表1模擬實驗條件，3種方法模擬二維潰壩弧形邊界的運行時間見表2。

由圖8和圖9及表2可知，本文方法在穩定性和計算效率方面要優于傳統邊界力法及虛粒子法，并且隨著粒子數的增加，本文方法的耗時增長慢于其他2種方法，計算效率更高。

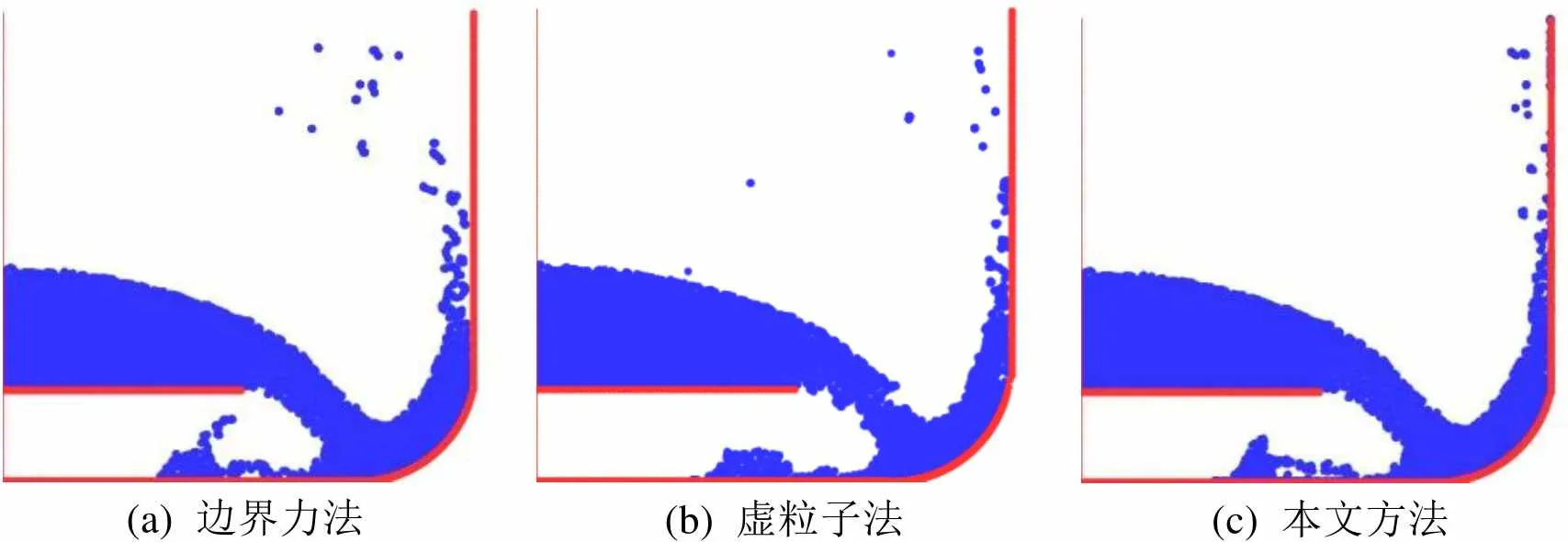
(a) 邊界力法(b) 虛粒子法(c) 本文方法

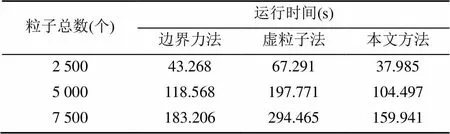
表2 3種方法模擬二維潰壩弧形邊界的運行時間

3.2 復雜場景模擬

圖10和圖11為3種方法模擬液體在漏斗和弓形水管的運行場景以及邊界處理效果。

由圖10和圖11可知，圖10(c)為本文方法模擬漏斗的場景，上壁未出現明顯的粒子飛散情況；圖11(c)為模擬弓形水箱場景，流體流動的整體穩定性較好，且粒子分布更均勻。說明本文方法在模擬復雜場景時的穩定性更好，適用范圍更廣。

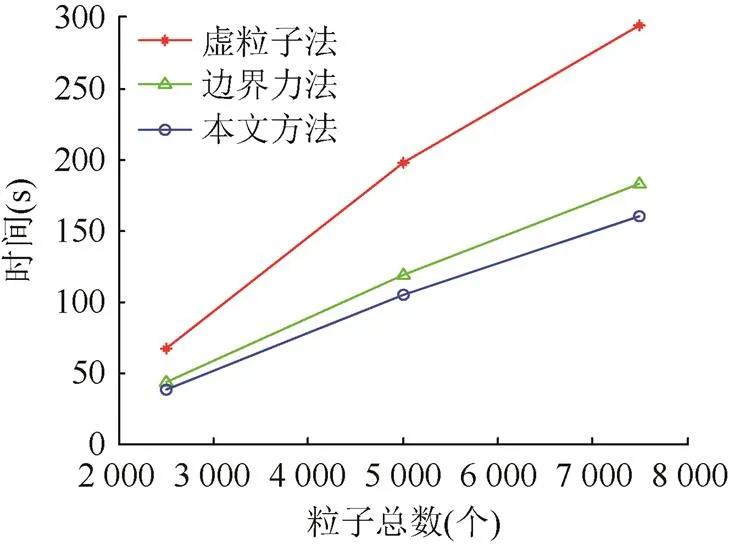
圖9 隨著粒子數的增加，邊界力法、虛粒子法和本文方法耗時增長對比

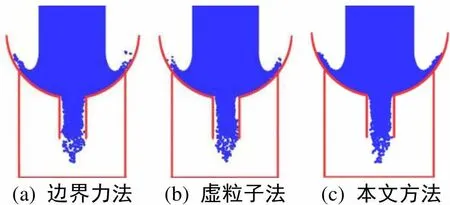
(a) 邊界力法(b) 虛粒子法(c) 本文方法

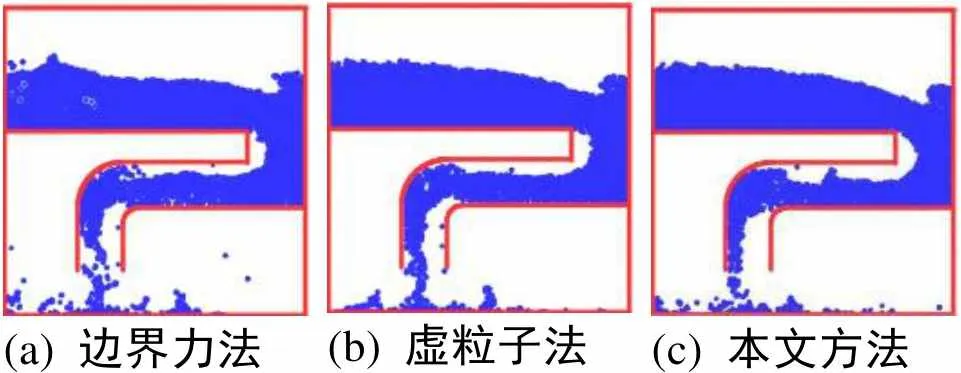
(a) 邊界力法(b) 虛粒子法(c) 本文方法

4 結 論

針對傳統的邊界力法和虛粒子法的不足，本文提出一種基于速度修正的固壁邊界處理方法，既不需要求解邊界力也無需在邊界外生成虛粒子，直接利用動量方程和計算速度耗損量求出流體粒子遇到邊界后的反彈速度，大大降低了處理邊界的復雜程度，也克服了邊界力法和虛粒子法在邊界拐角處粒子不均勻采樣而導致的算法不穩定的問題。模擬仿真結果表明本文方法的穩定性、計算效率均比傳統的2種方法更好，且隨著粒子數的增加，本文方法的耗時增長也比上述2種方法慢，計算效率高的優勢更明顯；通過模擬一些復雜場景，本文方法未出現粒子飛散情況，穩定性好，適用范圍更廣。

[1] MONAGHAN J J. Simulating free surface flows with SPH [J]. Journal of Computational Physics, 1994, 110(2): 399-406.

[2] MüLLER M, SCHIRM S, TESCHNER M, et al. Interaction of fluids with deformable solids [J]. Computer Animation and Virtual Worlds, 2004, 15(34): 159-171.

[3] HARADA T, KOSHIZUKA S, KAWAGUCHI Y. Smoothed particle hydrodynamics in complex shapes [J/OL].[2018-10-11].https://dl.acm.org/citation.cfm?id=2614375.

[4] BECKER M, TESSENDORF H, TESCHNER M. Direct forcing for Lagrangian rigid-fluid coupling [J]. IEEE Transactions on Visualization and Computer Graphics, 2009, 15(3): 493-503.

[5] MONAGHAN J J, KAJTAR J B. SPH particle boundary forces for arbitrary boundaries [J]. Computer Physics Communications, 2009, 180(10): 1811-1820.

[6] LIU M B, SHAO J R, CHANG J Z. On the treatment of solid boundary in smoothed particle hydrodynamics [J]. Science China (Technological Sciences), 2012, 55(1): 244-254.

[7] RANDLES P W, LIBERSKY L D. Smoothed particle hydrodynamics: Some recent improvements and applications [J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1-4): 375-408.

[8] MORRIS J P, MONAGHAN J J. A switch to reduce SPH viscosity [J]. Journal of Computational Physics, 1997, 136(1): 41-50.

[9] LIU M B, LIU G R, LAM K Y. Investigations into water mitigation using a meshless particle method [J]. Shock Waves, 2002, 12(3): 181-195.

[10] HU X Y, ADAMS N A. A multi-phase SPH method for macroscopic and mesoscopic flows [J]. Journal of Computational Physics, 2006, 213(2): 844-861.

[11] SCHECHTER H, BRIDSON R. Ghost SPH for animating water [J]. ACM Transactions on Graphics, 2012, 31(4): 1-8.

[12] 劉虎, 強洪夫, 陳福振, 等. 一種新型光滑粒子動力學固壁邊界施加模型[J]. 物理學報, 2015, 64(9): 384-397.

Treatment of Solid Boundary Based on Velocity Correction

ZHU Xiao-lin, CHEN Wei

(School of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China)

The study of solid boundary treatment method has been a difficult problem in fluid simulation. The common methods of solid boundary treatment are boundary force method and virtual particle method. The boundary force method prevents fluid particles from penetrating the boundary by exerting force on the fluid particles near the boundary, but this method has too many parameters and the force is difficult to adjust, and the boundary truncation error will occur in the calculation. The virtual particle method solves the problem of boundary truncation error by generating virtual particles outside the boundary. However, when dealing with complex boundary problems, the generation of virtual particles is difficult, and the calculation accuracy will be affected due to the uneven distribution of virtual particles, which leads to particles to disperse. To solve these problems, the paper presents a new method for the treatment of solid boundary based on velocity correction, which does not need to solve the boundary force or generate virtual particles outside the boundary. The momentum equation and the velocity consumption are used directly to calculate the rebound velocity of the fluid particles when they hit the boundary, which greatly reduces the complexity of the boundary treatment. It also overcomes the problem of the instability of the boundary force method and the virtual particle method caused by the uneven sampling of particles at the corner of the boundary. Simulation results show that the proposed method is more stable and more efficient than traditional methods above, and with the increase of the number of particles, the time consuming of this method is also slower than that of the two methods, and the advantage of high computational efficiency is more obvious and the simulation effect of complex scene is also better.

fluid simulation; solid boundary; boundary force method; virtual particle method; velocity correction

TP 391.9

10.11996/JG.j.2095-302X.2019040637

A

2095-302X(2019)04-0637-07

2019-01-30；

定稿日期：2019-03-20

國家自然科學基金項目(61272024)

朱曉臨(1964-)，男，安徽池州人，教授，博士，碩士生導師。主要研究方向為數值逼近、計算機圖形學、CAGD、圖形圖像處理等。 E-mail：zxl_hfut@126.com