基于間隙浮動的行星齒輪傳動系統靜態均載特性分析

董 皓，劉志宇，張建文

(西安工業大學 機電工程學院，陜西 西安 710021)

0 引言

行星輪系優點諸多[1]，被廣泛應用于航空發動機、船舶主推進系統、車輛傳動裝置以及直升機主減速器等裝置中。目前，國內外學者分別從理論和實驗兩個方面對行星齒輪傳動系統的均載問題做了大量研究。Kahraman和Ligata[2-3]等通過靜力學理論模型和實驗對行星齒輪傳動系統的均載問題進行了研究；Boguski和Nishino[4]提出一種新的方法用以測量行星齒輪傳動系統的均載特性和太陽輪的浮動軌跡；Montestruc[5-6]通過數值方法計算了行星齒輪傳動系統的均載模型，分析了各誤差因素對均載特性的影響；周璐[7]通過建立動力學均載分析模型，研究了誤差對行星傳動系統均載特性影響；朱增寶[8]分析了支撐剛度對行星傳動系統動態均載特性的影響；陸俊華[9]從動力學角度建立2K-H型行星傳動系統的計算模型，研究了系統的均載特性；杜進輔[10]等提出一種基于變形協調條件的行星輪系靜態均載特性分析方法。還有一些學者對功率分流的均載力學特性進行了大量的研究[11-15]

本文以應用于風電行業的六行星輪齒輪傳動系統為研究對象，從靜力學角度分析了該系統的均載特性。根據功率流動閉環特點，建立考慮制造、偏心誤差、間隙浮動和徑向浮動的系統整體變形協調條件。運用當量嚙合誤差理論，結合力矩平衡條件，建立了考慮各影響因素的靜態均載力學模型。通過引入輪齒承載接觸仿真分析方法，計算了模型中各齒輪副的時變嚙合剛度。分析各誤差對均載系數的影響，研究花鍵間隙浮動和徑向浮動對系統均載特性的影響。

1 力學平衡方程建立

圖1是行星齒輪傳動系統的運動簡圖[9]。其中，輸入扭矩T1(輸入轉速ns)經太陽輪Zs分流給i個行星輪ZPi(i=1,2,…,6)，行星輪ZPi與內齒圈Zr進行嚙合，將輸出功率經行星輪ZPi匯流到行星架C上，由與行星架C固聯的輸出軸進行輸出，輸出扭矩為Tout，輸出轉速為nc。建立如圖2所示的靜力學平衡關系模型，設定系統輸入扭矩T1(輸入轉速ns)為逆時針方向旋轉，太陽輪S對各行星輪Pi(i=1,2,…,6)的作用扭矩為Tspi，各行星輪Pi對太陽輪S的反作用扭矩為Tpis，各行星輪Pi和內齒圈r的作用扭矩和反作用扭矩分別為Tpir和Trpi，規定主動扭矩為正，負載扭矩為負；Kspi表示太陽輪和行星輪Pi之間的等效輪齒嚙合剛度；Kpir表示行星輪Pi和內齒圈r之間的等效輪齒嚙合剛度；Ks和Kr分別表示太陽輪和內齒輪支承處的等效彈性支撐剛度；rbs、rbp和rbr分別表示太陽輪、行星輪和內齒圈的基圓半徑；Ks和Kr表示太陽輪和內齒圈的彈性支撐剛度。

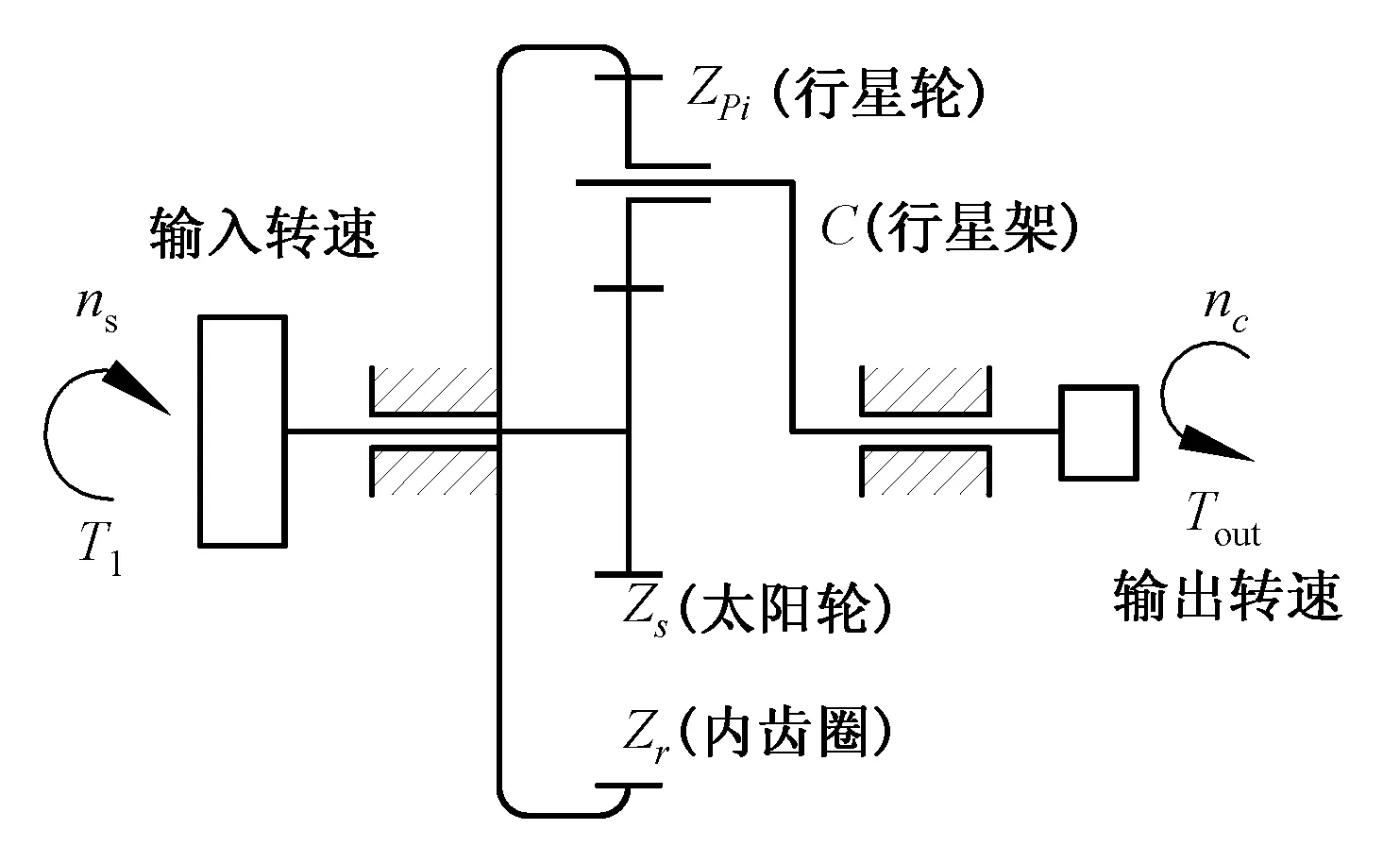
圖1 2K-H行星傳動系統的運動簡圖
Fig.1 Kinematic sketch of 2K-H planetary transmission

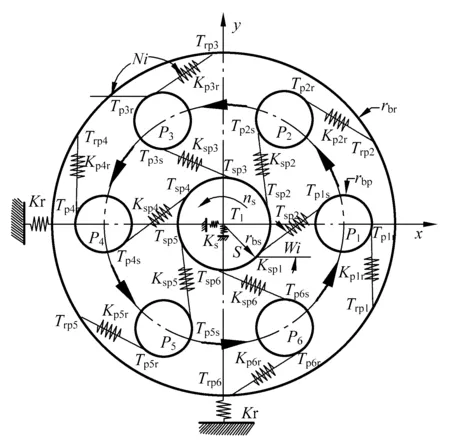
圖2 靜力學平衡關系示意圖
Fig.2 A diagram of static equilibrium relationship

得到靜力學扭矩平衡條件為

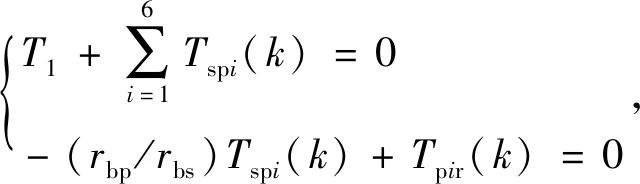
(1)

式中，i=1,2,…,6，Tij(k)(ij=spi、pir)表示在一個嚙合周期中被動輪j對主齒輪i在第k(k=1,2,…,5)個嚙合位置扭矩。

圖3表示了系統各齒輪的扭轉角關系。

圖3 各齒輪扭轉角關系示意圖
Fig.3 Schematic diagram of the relationship between the torsion angle of the gear

圖3中，Δφpi表示各行星輪Pi的扭轉角；Δφs表示太陽輪S的扭轉角；Δφr表示內齒圈r的扭轉角；Δφspi表示太陽輪在扭矩作用下相對于行星輪Pi的扭轉角變形；Δφpir表示行星輪Pi在扭矩作用下相對于內齒圈的扭轉角變形，嚙合轉角滿足

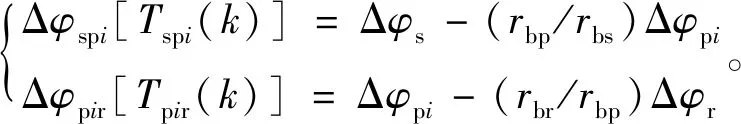
(2)

由于Δφspi和Δφpir分別是Tspi(k)和Tpir(k)的函數，將i(i=1,2,…,6)個行星輪嚙合傳動誤差換算為相對于太陽輪S的當量嚙合誤差，可得

Δφi=Δφspi[Tspi(k)]+(rbp/rbs)Δφpir[Tspi(k)]=

Δφs-(rbr/rbs)Δφr。

(3)

由于Δφ1=Δφi(i=2,3,…,6)，可以得到基于功率流動閉環特性的系統扭轉角變形協調條件為

Δφsp1[Tsp1(k)]+(rbp/rbs)Δφp1r[Tsp1(k)]=

Δφspi[Tspi(k)]+(rbp/rbs)Δφpir[Tspi(k)]。

(4)

2 當量嚙合誤差和均載系數計算

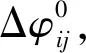
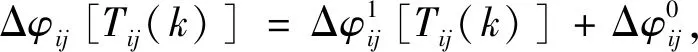
(5)

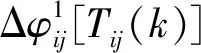
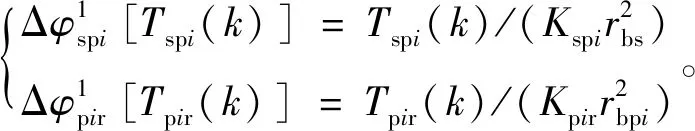
(6)

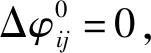
2.1 誤差引起的累積綜合嚙合誤差

制造誤差E和安裝誤差A的方向角以β和γ表示[9]，引起的角位移誤差可由

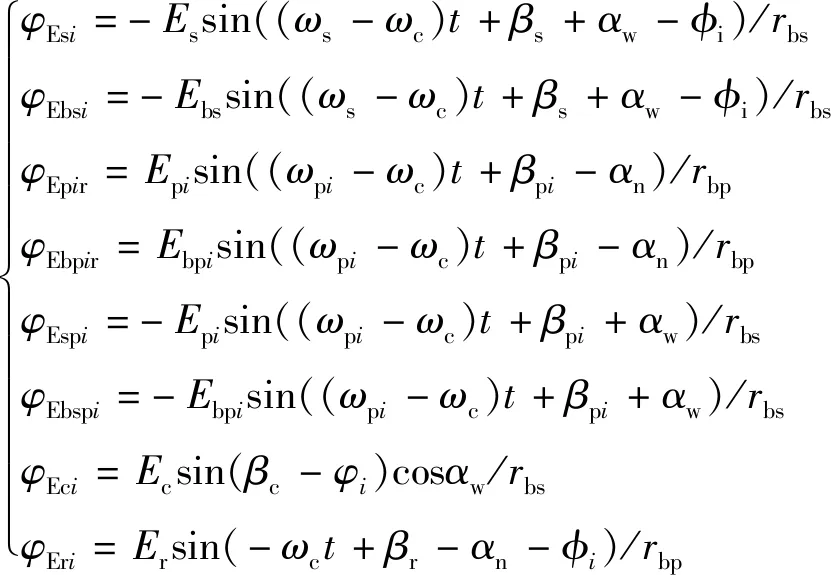
(7)

表示，其中，由太陽輪制造誤差Es引起的角位移φEsi，太陽輪軸承制造誤差Ebs引起的角位移φEbsi，第i個行星輪的制造誤差Epi引起的內嚙合角位移φEpir和外嚙合角位移φEspi，第i個行星輪聯接軸軸承的制造誤差Ebpi引起的內嚙合角位移φEbpir和外嚙合角位移φEbspi，行星架制造誤差Ec引起的角位移φEci，內齒圈制造誤差Er引起的角位移φEri。

由太陽輪安裝誤差As引起的角位移φAsi，第i個行星輪的安裝誤差Api引起的內嚙合角位移φApir和外嚙合角位移φAspi，內齒圈安裝誤差Ar引起的角位移φAri，可以分別表示為

(8)

其中，ωs、ωpi和ωr分別為太陽輪、星輪和內齒輪的角速度；αw和αn分別表示外嚙合齒輪傳動與內嚙合齒輪傳動的嚙合角；φi為第i個行星輪相對于第1個行星輪的位置角，φi=2π(i-1)/6。

將式(7)和(8)的誤差分別等效轉換為太陽輪和行星輪spi以及行星輪與內齒圈pir的內外嚙合線上，形成當量嚙合誤差，并逐次分別疊加，得累積當量嚙合誤差φspi和φpir為[14]

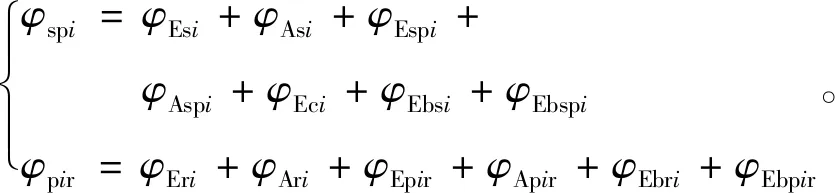
(9)

設太陽輪、內齒圈沿x、y向的軸心浮動位移量分別為xs、ys、xr、yr，則浮動構件引起的角位移φsi與φri分別為

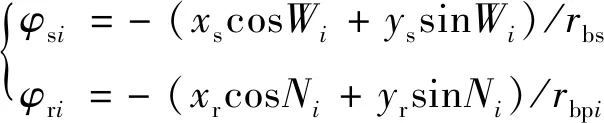
(10)

式(11)中，Wi和Ni分別如圖1所示的角度關系，Wi表示太陽輪與第i個行星輪嚙合線的方位角，Wi=ωct+π/2-αw+φi，Ni表示第i個行星輪與內齒圈嚙合線的方位角，Ni=ωct+π/2+αn+φi。

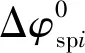
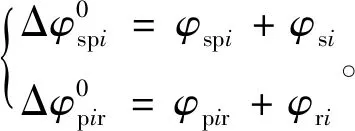
(11)

將式(6)和式(11)代入式(5)，得各齒輪副嚙合傳動誤差Δφspi[Tspi(k)]和Δφpir[Tpir(k)]為

(12)

將式(12)帶入到式(4)可以得到當量嚙合誤差因素影響下的系統完整變形協調條件為

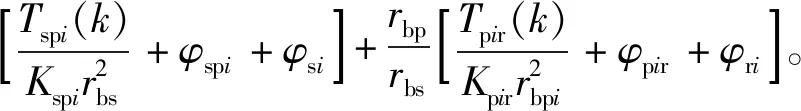
(13)

2.2 花鍵間隙浮動平衡條件

太陽輪浮動過程中，受到6個與之相嚙合的行星輪的嚙合力Tspi以及花鍵聯接軸的支承反力的共同作用。由于內外花鍵之間存在徑向間隙，如果太陽輪受力不均衡，會產生徑向的微移動，直至受力趨于均衡，而太陽輪受花鍵軸的約束不能完全自由浮動。

在花鍵傳遞扭矩的過程中，內、外花鍵摩擦力為Fm，Fm=τFN，FN表示內外花鍵之間的正壓力，τ為摩擦系數，內、外花鍵的徑向間隙量L=S2-S1。太陽輪在一個嚙合周期中，產生的浮動量為

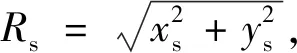
(14)

式中，xs和ys表示在x和y方向的浮動量。

當支承反力小于摩擦力Fm時，內、外花鍵之間不產生滑移，在滿足系統強度要求的條件下，由花鍵軸的彎曲變形適應太陽輪的位置變化，當支承反力大于摩擦力Fm時，內、外花鍵之間產生滑移，由滑移量適應太陽輪的位置變化，當內、外花鍵消除了徑向間隙時，重新由花鍵軸的彎曲變形適應太陽輪的位置變化，因此，太陽輪的支承反力在x、y向的分量引起的平衡方程可以表示為[15]

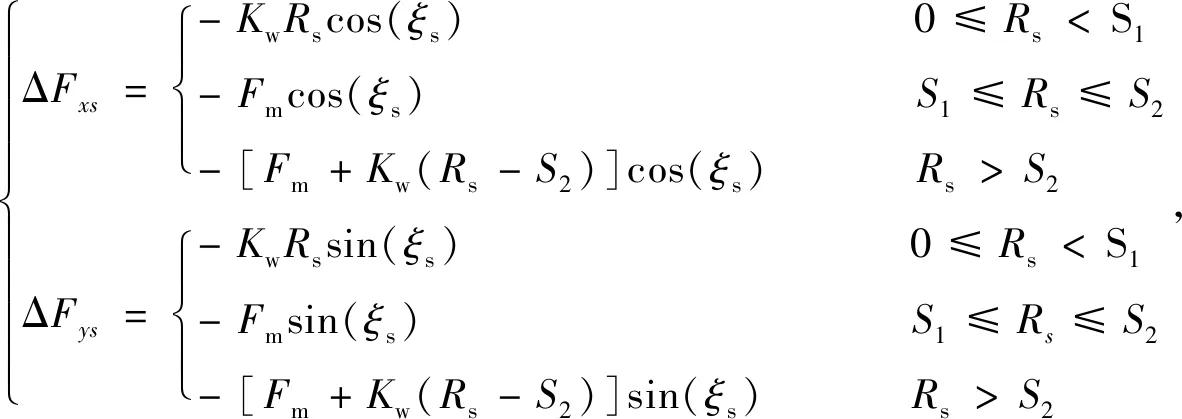
(15)

式中，花鍵軸的彎曲剛度Kw=EIz，E為彈性模量，Iz為花鍵軸的慣性矩；ξs表示向量xs、ys的方向角。

將式(15)聯立其它各構件的支承平衡條件和力矩平衡條件以及變形協調條件，建立間隙非線性數學模型，可以求解得到系統的均載系數。

2.3 均載系數求解

考慮太陽輪花鍵間隙浮動和內齒圈徑向彈性浮動引起的靜力平衡，得到平衡方程

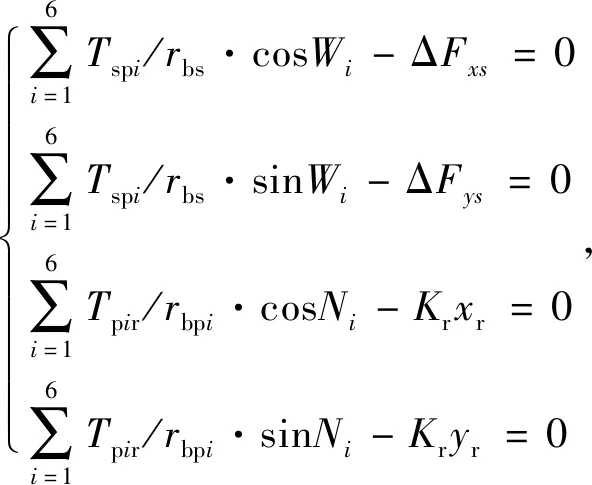
(16)

聯立式(1)、式(13)和式(16)，可以求出各齒輪副的傳遞扭矩Tspi(k)和Tpir(k)，從而求得各行星輪的均載系數為Jpi=Tspi(k)/(T1/6)，系統的均載系數為J=(Jpi)max，均載系數的大小表征著系統的均載特性的好壞，均載系數越大，系統均載特性越差。

3 均載特性的影響分析

系統各參數如表1所示。其中，給定輸入轉速ns=85.9 r/min，輸入功率為82.18 kW，太陽輪和內齒圈的支撐剛度為Kr=9.42×109N/m。各誤差值均取3 μm。給定內外花鍵摩擦系數τ=0.1，內外花鍵之間的正壓力FN=1.14×105N，花鍵軸的支撐彎曲剛度為Kw=9.16×1010N/m。

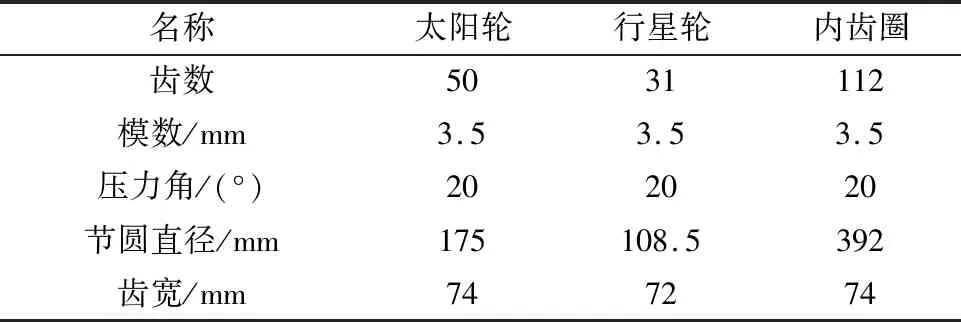
表1 各齒輪的主要參數數據Tab.1 Main parameters of the gear data

根據文獻[13-15]，利用LTCA仿真分析方法計算得到時變嚙合剛度曲線如圖4所示，太陽輪和行星輪spi的嚙合剛度在1.391×109N/m處波動，行星輪和內齒圈pir的嚙合剛度在1.533×109N/m處波動。

3.1 誤差因素對均載特性的影響

制造誤差和安裝誤差作用時的系統均載系數如圖5所示，此處，行星輪的制造誤差和安裝誤差為各行星輪內外嚙合各誤差因素的疊加。

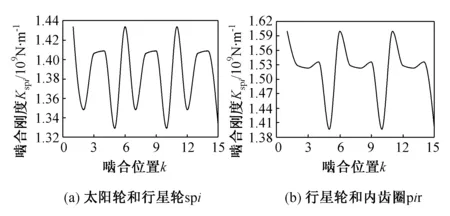
圖4 各齒輪副時變嚙合剛度
Fig.4 The time varying meshing stiffness of each gear pair

計算得到Es、Epi和Er影響的均載系數分別為1.132 6、1.090 7和1.132 6，As、Api和Ar影響的均載系數分別為1.132 6、1.085 2和1.132 6。Es、Epi、Er、As和Ar影響的均載系數呈周期性變化，Api和Ec影響的均載系數隨時間為固定值。太陽輪和內齒圈的制造和安裝誤差影響下的系統均載系數為1.132 6，兩者峰值一樣，制造誤差的影響頻率高于安裝誤差，行星輪的制造誤差比安裝誤差影響的均載系數值略大。

圖5 制造誤差和安裝誤差單獨作用時的系統均載系數
Fig.5 Load sharing coefficient of system when manufacturing error and installation error are acted separately

以制造誤差Es、Epi、Er和Ec為例，給出各主要制造誤差單獨變化時的均載系數，如圖6所示。

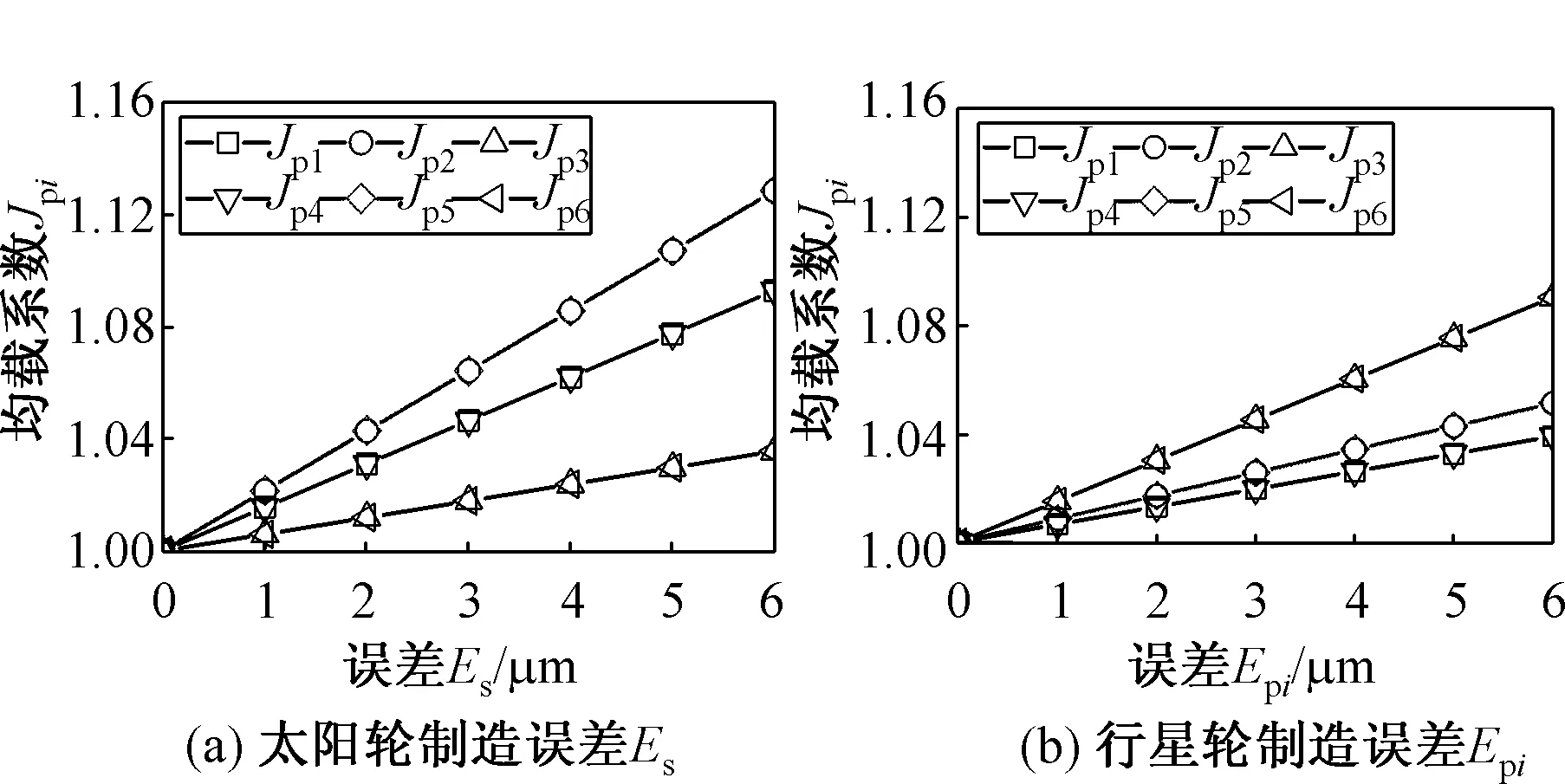
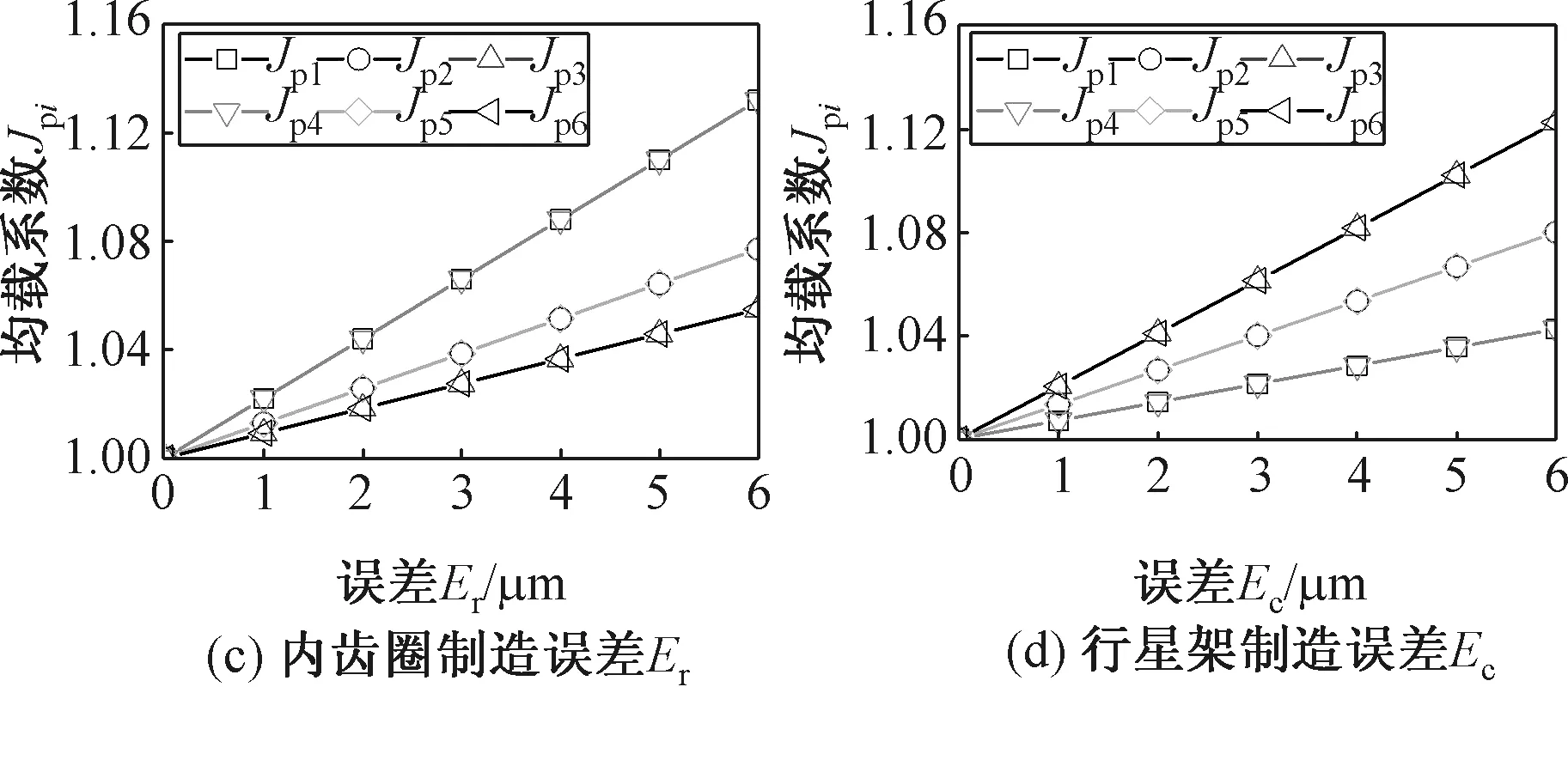
圖6 各主要制造誤差單獨變化時系統均載系數
Fig.6 System load-sharing coefficient when each major error changes individually

隨著各構件誤差值的增大，系統均載系數均變大，其中太陽輪和內齒圈的制造誤差影響最大，行星架影響次之，行星輪的影響較小。

3.2 浮動因素對均載特性的影響

以給定Ep2=3 μm為例，計算了花鍵間隙量從0 mm到0.2 mm對應的系統均載系數如圖7所示。

圖7 不同花鍵間隙量影響的系統均載系數
Fig.7 Load coefficient of system with different spline clearance

在間隙量分別為0.0 mm、0.04 mm、0.1 mm和0.2 mm時，計算得到系統的均載系數分別為1.379 6、1.315 7、1.219 8和1.094 9。間隙量為0.2 mm時，達到浮動條件。在不滿足完全浮動之前，系統均載系數的變化隨時間呈非線性變化，當隨著間隙量的增大，達到完全浮動時，即內外花鍵的滑移量適應太陽輪的位置變化，均載系數又呈周期性變化，整體均載特性有所改善。

圖8給出了Ep2在誤差0 μm、3 μm、6 μm和10 μm下時各行星齒輪均載系數隨花鍵間隙量變化的情況,可以看出，隨著間隙量的增大，均載系數逐漸減小，最終達到均載。給定誤差Ep2下的行星輪2的均載系數影響最大。花鍵間隙量為0 mm時，完全由軸的彎曲適應浮動輪的位置變化。隨著誤差的增大，系統達到均載時所需的花鍵間隙量也增大。給定幾組誤差下最終達到均載時的系統均載系數分別為1.063 32、1.126 6和1.316 1。

圖8 均載系數隨間隙量變化
Fig.8 Load coefficient changed with spline clearance

當給定制造誤差和安裝誤差共同作用時，誤差量均為3 μm，得到均載結果如圖9所示，同時給出太陽輪和內齒圈浮動對系統載荷分配的影響，此時，給定內齒圈的彈性浮動支撐剛度為Kr=9.42×106N/m，給定太陽輪浮動時的花鍵間隙量為0.3 mm。

由圖9可以看出，當誤差共同作用時，不浮動條件下，各行星輪i(i=1,2,…,6)上的均載系數分別為1.334 1、1.456 0、1.356 5、1.259 8、1.123 3、1.187 5，得到系統的均載系數為1.456 0。三種浮動狀態下(如圖(b)、(c)、(d)所示)的均載系數分別為1.023 6，1.018 7，1.012 0，內齒圈單獨完全浮動下要比太陽輪單獨完全浮動對均載特性的改善效果好。

圖9 誤差共同作用下的浮動均載系數
Fig.9 Floating load-sharing coefficient under the common effect of error

4 結論

1) 通過引入齒輪承載接觸仿真方法，真實地反應了各嚙合位置的均載力學情況。推導了系統的變形協調條件，從本質上反映了由構件彈性變形導致的均載問題。

2) 均載系數隨系統各誤差呈周期性變化，太陽輪和內齒圈的制造誤差影響頻率較安裝誤差大；隨著各構件誤差值的增大，系統均載系數均變大，其中太陽輪和內齒圈的制造誤差影響最大，行星架影響次之，行星輪的影響較小；

3) 當存在花鍵間隙時，系統均載系數隨時間變化呈非線性變化，當花鍵間隙量增大到一定程度時，均載系數又呈周期性變化。隨著間隙量的增大，均載系數逐漸減小，最終達到均載，給定誤差Ep2下的行星輪2的均載系數影響最大。

4) 太陽輪間隙浮動和內齒圈徑向浮動能有效改善系統的均載特性，太陽輪和內齒圈同時浮動的效果更好，單獨浮動情況下，內齒圈的浮動效果要好。