高中物理中模型思維能力的培養
童鍇

【摘要】 ?物理是一門以觀察、實驗為主的學科,物理教學的基本任務是使學生掌握物理學的基礎知識和基本技能更重要的是使學生掌握研究問題的方法。而模型的變換對于高中生來說是一個重要的問題,本文中重要從模型變換的障礙和方式兩個方面來作一個簡單的研究。
【關鍵詞】 ?模型思維 模型變換 思維定式 表象干擾 等效變換 類比變換
【中圖分類號】 ?G633.7 ? ? ? ? ? ? ? 【文獻標識碼】 ?A ? 【文章編號】 ?1992-7711(2019)15-131-01
模型就是通過我們對問題現象的分解,利用我們考究得來的機理,吸收一切主要因素,略去一切不主要因素所創造出來的一幅圖畫。所謂模型思維,就是利用模型達到特定認識目的的思維方式。在物理教學活動中之所以要研究模型思維,是因為它不但是推動物理學進展的重要的思維方式,而且是教好、學好物理課程的重要的思維方式。
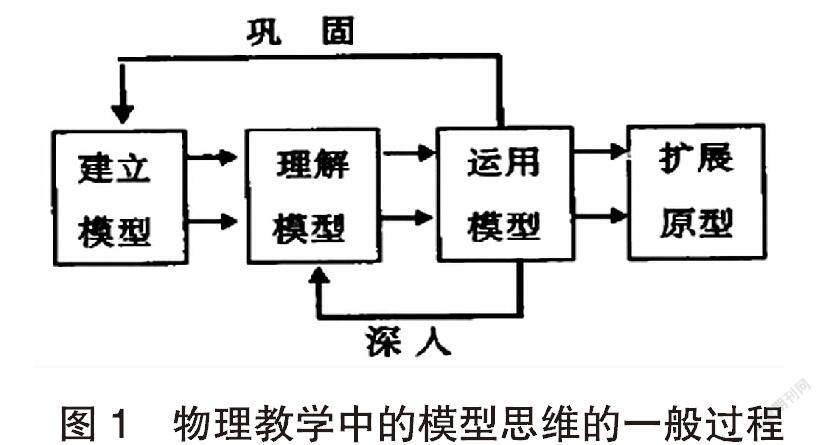
物理教科書中有許多理想化模型,如研究對象的理想化模型有質點、剛體,彈簧振子,單擺,理想氣體,勻強電場、點電荷,薄透鏡等;物理過程的理想化模型有勻速直線運動,簡諧振動,理想氣體的等溫變化,鏡面反射等。物理模型是物理實體的近似反映,實際物體要經過合理的近似處理才能模型化。但是,由于模型突出了事物的主要因素,忽略了次要因素,因此物理模型不但反映了事物的本質特征,而且使研究過程大大簡化。因此物理模型教學的一般過程可用下圖表示
許多學生反映物理課聽起來有趣,做起來(做練習)難。他們的困難,往往不在于記不住某個物理公式,而在于對一個新情景問題不知道該用什么公式。換句話說,就是不善于將一個具體問題轉換成某一物理模型,因此,加強中學生模型變換能力的培養對于其模型思維的發展將顯得尤為重要。即,模型思維能力的培養重在模型變換能力的培養。
1.模型變換的主要障礙
1.1思維定勢
在教學過程中,尤其在建立模型時,教師往往強調了模型的理想化而忽視其可變性,即模型可以靈活變換,廣泛運用,使學生在思想上產生模型的絕對化傾向,妨礙了思維的開展。
例l,已知質量是0.99kg的物體M放在光滑圓弧軌道OA的最低點O,質量為m=0.01kg的子彈以100m/s的速度水平擊中物體M并留在其中,求物體從開始運動到返回O點所用的時間(圓弧軌道半徑為39.2m)。
學生能根據系統碰撞前后動量守恒求出物體獲得的速度V。物體獲得速度V后沿圓弧軌道的運動是變速曲線運動,題目又未給出弧長或它所對圓心的張角,在中學階段按常規方法無法求解。但仔細分析物體的受力情況后,不難發現它受重力和軌道的支持力作用完全類似于單擺的受力情況。這就啟發我們:能否用單擺模型求解?通過計算知道,物體在圓軌道最高點與最低點的半徑夾角,這樣,可把物體在圓弧軌道上的運動歸結為單擺模型,巧妙地用單擺周期公式求出t=4s。造成學生不會聯想到用單擺模型來解的根源在于單擺模型教學中的思維定勢,認為單擺總是懸掛著且擺球上只能受到重力和擺線的拉力作用而在最低點附近振動。
1.2表象干擾
學生在分析物理問題時,思維的焦點往往集中在問題的表面現象上,對于陌生的物理模型缺乏辨異識同,無法把知識運用到未知現象中去,即不善于排除表象干擾抓住本質因素,將題中的物理模型與熟悉的物理模型相比較,分析異同并尋找出內在的聯系和相同點,建立起熟悉的模型與未知現象的關系。
例2.在光滑的水平軌道上有兩個半徑都是r的小球A和B,質量分別為m和2m,當兩球心間的距離大于I(I比2r大得多)時,兩球之間無相互作用力:當兩球心間的距離等于或小于l時,兩球間存在相互作用的恒定斥力F.設A球從遠離B球處以速度v0沿兩球連心線向原來靜止的B球運動。欲使兩球不發生接觸,v0必須滿足什么條件?
該題描述的物理模型與教材中分子球的相互作用,如圖2所示,求彈簧的最大勢能等,都屬于相互作用的問題,所不同的是本題中相互作用的是“恒力”而不是變力。平時用動量守恒和功能關系來解碰撞中壓縮過程中的問題訓練也不少。學生打不開思路的關鍵是被題設中的一個抽象的斥力迷惑。若能與熟悉的兩物體作完全排彈性碰撞模型類比,并運用其結論,必將觸發靈感,啟迪思路:兩球將接觸而未接觸時系統損失的動能最大,且損失的動能全部轉化為系統的斥力勢能,此時刻A、B球應具有相同的速度。
2.模型變換的兩種方式
2.1等效變換
等效的思想是物理學研究的基本思路之一,教材中不乏其例,前面例1中介紹的分析方法便是一種等效變換方法。又如:導線電阻為R,做成一個閉合圓環,半徑為r,一直導線以速度V運動,環放在磁感應強度為B的習強磁場中,直導線電阻不計,則運動到圓心處的瞬間,直導線中的電流為多少?
當直導線經速度V的運動時,直導線兩端會產生感生電動勢,由于整個回路是閉合的,故圓環中有感生電流產生。這時,直導線相當于一個電源。這種情況與圖所示電路等效,若能作這樣等效變換,那么本題就變得簡單易解了。
2.2類比變換
物理學中有許多事物或現象之間的關系具有相似性,這就為我們進行類比變換提供了依據。
例3,一長為l的細繩,上端固定,下端拴一質量為m的帶電小球,將它置于場強大小為E的水平向右的勻強電場中,當處于平衡時,細線與豎直方向成a角(α≤45°)。如果使偏角由a增大到φ,然后由靜止釋放,則φ應多大才能使細線到達豎直位置時,小球的速度剛好為零。
本題的原型是重力場中的單擺模型,現在小球不僅受到重力作用,同時還受到電場力作用,若將這兩個力合為一個力,則容易判斷小球的平衡位置在O點。小球從A點釋放后,在A、B之間來回振動的模型若與原型類比,則小球相當于懸掛在一個特殊場中的擺球。由原型的結論推知:小球通過平衡位置O時速度最大,在兩振幅位置A、B時速度為零。由于對稱性可判定φ=2α.
在模型變換教學中,教師是導游,是引路人,學生則是領略大自然勝境,進而改造自然的主人。這樣,簡繁有致,逐漸深人,學生的模型變換能力就有效地建立起來。

