分數延時濾波器設計與研究
徐 宇,安 濤,楊祎綪
(中國船舶重工集團公司第七二三研究所,江蘇 揚州 225101)
0 引 言
分數延時濾波器是指一種可以延時分數個采樣間隔的數字濾波器。在雷達對抗領域,主要用于相控陣雷達接收端和數字多波束干擾機發射端的相位延時控制。常用的分數延時設計方法有2種:第1種是通過把數字信號轉變成帶寬受限的連續信號,再進行精確延遲后重新采樣;第2種方法是通過設計有限脈沖響應(FIR)數字濾波器使得濾波器在整個有效帶寬內的幅度響應為1,并且在相位上有理想分數延時特性[1],本文是研究的后一種方法。
1 數字波束形成原理
數字波束形成技術是通過數字技術實現波束形成,如圖1所示,廣泛應用于電子對抗、相控陣雷達和通信領域。為了獲得高距離分辨率、低旁瓣的能力,相控陣雷達必須要擁有大的瞬時帶寬。對于傳統的寬帶數字陣雷達,傳統的波束形成方法經常會引起主瓣寬度變寬,天線波束掃描不準,這是因為傳統的波束形成網絡里面的延時精度不準,做不到精確補償引起的,這就需要引入分數延時濾波器。
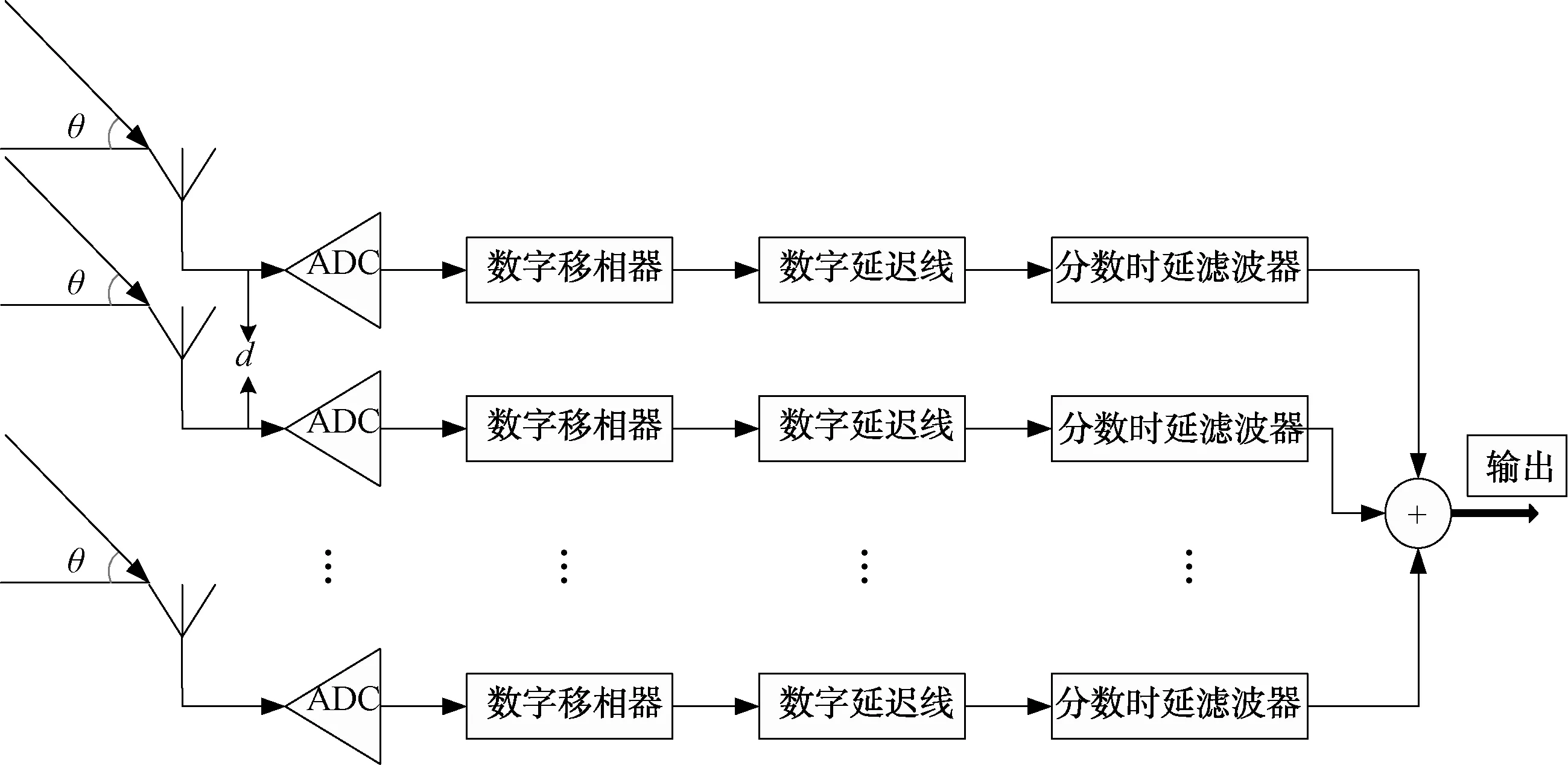
圖1 寬帶陣列數字波束形成結構
常見的寬帶雷達信號是經過載波調制的脈沖,可以用數學表達式表示為:
(1)

(2)
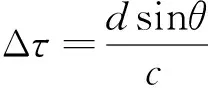
(3)
其基帶形式為:
(4)
比較式(2)和(4),可以發現,對式(4)第2項進行數字移相、第3項進行時延補償,就能使各陣元信號同相疊加,在預期的方向上波束形成。第k個陣元上的時延τk為:
(5)
采樣周期為T時,補償第k個陣元的時延是:
(6)
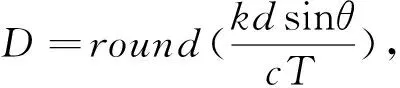
2 分數延時設計方法
一般對于輸入信號x(t)進行時延D,得到輸出信號:
y(t)=x(t-D)
(7)
對于采樣周期為T的離散信號有:
(8)
hd(n)=sinc(n-d)
(9)
式中:hd(n)為理想響應的分數延時濾波器。
由于延時數d通常不是一個整數,hd(n)往往會是一個非因果的系統。設Hd(ejω)為期望的頻率響應,有:
(10)
分數延時濾波器的目的是尋找有限長度的h(n)去逼近理想的hd(n)。這里引入頻域誤差函數去決定h(n)的系數:
E(ejω)=H(ejω)-Hd(ejω)
(11)
由上面的誤差函數可以看出,要使得實際的頻率響應越接近理想的頻率響應,那么E(ejω)就得越小。通過這種方法求解的均方誤差如下:
(12)
根據Parseval定理可以得到時域的表達式:
(13)
從上式可以看出要使均方誤差最小,h(n)得等于hd(n)。在均方誤差的準則中,理想的無限長沖擊響應最有效和最簡單的逼近方法是截斷。因此,有限長的沖擊響應濾波器可以表示為:
h(n)=hd(n),M≤n≤M+N
(14)
即:
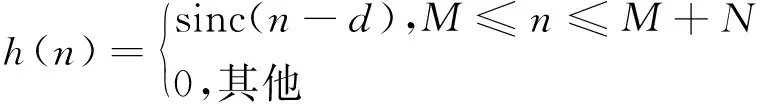
(15)
式中:M為沖擊響應的第1個非零值的下標,為了滿足因果系統,M的值需要大于0。
一般情況下設計一個低通的(0~απ)FIR濾波器,則有:
(16)
2.1 窗函數法
通常直接截斷的sinc函數會產生吉布斯效應,設計出來的分數延時濾波器往往達不到期望的要求。窗函數法能夠有效地改善吉布斯效應。窗函數法的實質是對時域的加權:
h(n)=w(n)*hd(n)
(17)

(18)
通常使用的窗函數有切比雪夫窗或者海明窗。此方法不但可以體現脈沖響應的中間值,還能減小峰值幅度誤差。采取加窗法設計分數延時濾波器的對理想響應的逼近程度取決于窗函數頻率響應的主瓣寬度和旁瓣幅度的尖峰值[2]。理想狀態下窗函數主瓣窄,旁瓣幅度低,但是由于選取的窗長度固定,很難達到理想狀態。一般情況下,隨著窗長度L的增加,主瓣寬度會隨之減小,而副瓣的幅度是由窗函數的形狀決定的,與窗的長度無關。
2.2 復頻響應法
窗函數法是在時域上去逼近理想分數延時濾波器,同樣可以通過對頻域誤差函數加權去逼近。原則上只需要關注帶寬內的誤差,因此只需要定義低通頻率的帶寬,從而得到誤差公式:
(19)
這里令濾波器的系數矩陣和離散傅里葉變換的因子矩陣為:
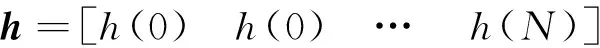
(20)
(21)
令:
C=Re{eeH}=
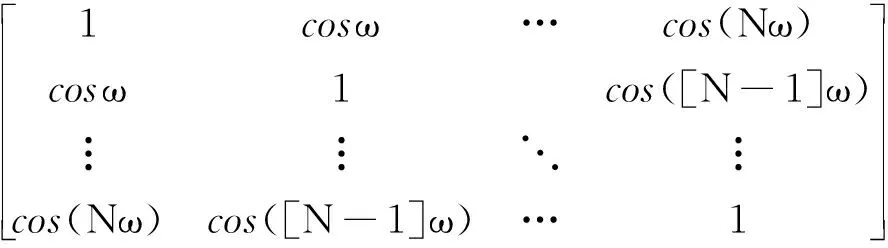
(22)
那么誤差公式可以簡化為:
E2=hTPh-2hTP1+p0
(23)
(24)
(25)
(26)
(27)
(28)
要使誤差達到最小,即E2對h求導使其等于0,得到:
2Ph=2P1=0
(29)
求得濾波器系數矩陣為:
h=P-1P1
(30)
此方法計算濾波器系數要求積分,復雜度與線性方程的個數成3次方正比,計算的代價比上面的方法大很多。
2.3 可變延時參數的Farrow結構法
上面的2種方法都是固定延時參數,而Farrow結構可以連續不斷地控制分數延時。這種方法是先計算好原型濾波器的系數,再用最小二乘曲線去擬合這個曲線。每個系數都是延時值d的Q階多項式,d的范圍是0~1,則:
(31)
那么濾波器的傳播函數可以表示為:
(32)
從上式可以看出,濾波器系數可以用幾個固定長度的濾波器以并行方式,通過延時d的冪指數來產生。
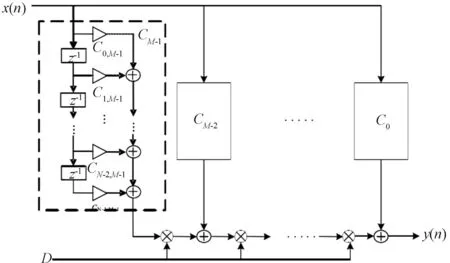
圖2 Farrow結構濾波器實現圖
由圖2可知,Farrow結構由M組N階FIR濾波器構成,其中虛線框圖中具體畫出了第M組N階FIR濾波器的內部結構,其余M-1組N階FIR濾波器的實現方式與之相同。Farrow結構所需要的濾波器階數遠大于前2種濾波器結構,運算量很大,它的優點是當時延變化時,僅改變時延參數D,就可以獲得不同的分數時延,不用重新加載系數,節省了存儲空間,降低了硬件實現的復雜度。
3 仿真分析
這一小節對上文中的幾種方法進行了仿真分析,對不同方法設計相同的濾波器階數和歸一化頻率,分析分數延時濾波器幅度頻率響應和相位延時響應特性。
在仿真過程中,4種方法都選擇設計階數為16階的分數延時濾波器,有效帶寬的歸一化頻率為0.8π,其中Farrow結構的濾波器系數曲線通過擬合的復頻響應法計算出來。圖3是4種方法的幅度頻率響應圖,分數延時濾波器實現的是數字時延,因此其幅度響應特性在線性時延帶寬中應該與全通濾波器一致,即濾波器的幅度頻率響應應該為1。從圖中可以看出,簡單的截斷不加窗函數的方法在通帶和阻帶在1附近有較大的波動,吉布斯現象明顯,而通過添加切比雪夫窗可以明顯改善吉布斯效應,在整個有效帶寬內獲得的幅度基本為1。復頻響應法相比于切比雪夫窗函數法,有效帶寬更加寬,過渡帶更窄;而通過Farrow結構去擬合的方法,可以發現幅頻特性基本一致。
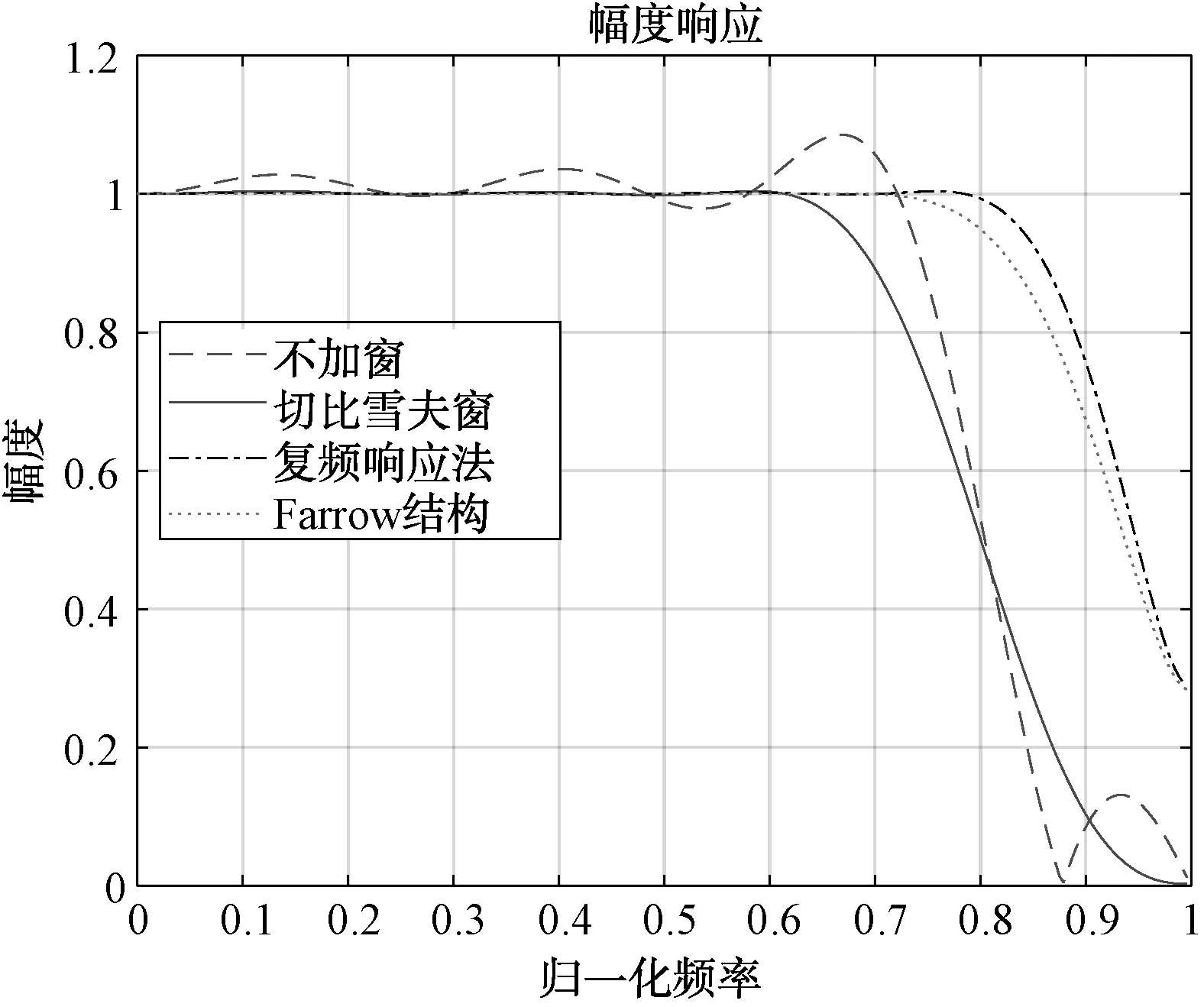
圖3 幅度頻率響應圖
圖4是4種方法的延時響應曲線圖,本文選取16階的分數延時濾波器理論值為7.4個采樣周期。從圖中可以看出,不加窗直接截斷的相位延時特性在有效帶寬內比較差,上下浮動接近0.1個采樣周期,而簡單的加切比雪夫窗后,得出的相位延時在通帶內只有0.02個采樣周期的誤差。復頻響應法雖然計算特別復雜,但是得到的效果最好,基本與理想曲線一致。Farrow結構法的相位延時特性同樣能夠接近復頻響應法的相位延時特性。
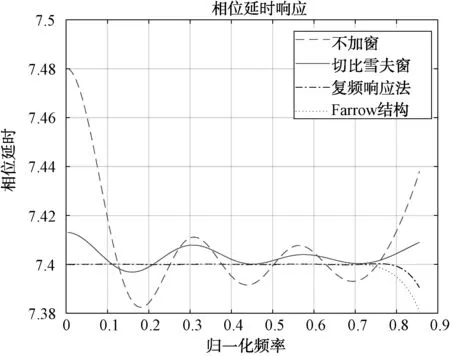
圖4 群延時響應圖
4 結束語
本文闡述了數字波束形成原理,并對分數延時濾波器進行了多種算法的推導和仿真,對比它們的性能。分數延時濾波器是數字波束形成技術中的核心,能夠應用于同時多波束干擾機,解決以前干擾多部目標需要分時干擾和分子陣同時干擾的功率不足問題。

