基于用戶特征和相似置信度的協同過濾算法

(河南理工大學 計算機科學與技術學院， 河南 焦作 454000)

網絡的普及提高了人們的生活質量，每天在我們所生活的這個世界出現了大量的信息，信息的增長速度絕對是一件近乎恐怖的事情——我們稱之為“信息爆炸”[1]。面對如此多的信息，較快地獲取用戶想要的或感興趣的信息變得較為困難。推薦系統可以推薦給用戶有用的信息，減少了用戶獲取信息的時間和精力。協同過濾推薦技術是在推薦系統中應用最早和最為成功的技術之一，因其可以充分利用信息間的聯系，執行效率高，能夠得到較好的推薦結果，因而成為當前研究的熱點[2]。

協同過濾一般采用最近鄰技術，利用用戶的歷史喜好信息計算用戶之間的距離，再利用目標用戶的最近鄰居用戶對商品評價的加權評價值來預測目標用戶對特定商品的喜好程度，從而根據這一喜好程度來對目標用戶進行推薦[3]。對于新用戶而言是沒有歷史數據的，這就出現用戶冷啟動問題。針對此問題，魏琳東[4]等人采用了矩陣分解的方法和神經網絡映射的知識各自對興趣向量進行計算再融合。在現實生活中用戶并不是對每一個項目都進行評分等行為，這就帶來評分數據的稀疏性問題。針對此問題，王竹婷[5]等人用懲罰因子應對共同評分項較少的用戶，并用依據自信息量所得的項目權值修正傳統的相似度計算方法。

為了緩解算法存在的問題，本文提出一種基于用戶特征和相似置信度的協同過濾算法(Attributes and Similar Confidence Collaborative Filtering，ASCCF)。將置信度和用戶特征按比例引入到用戶之間的相似性計算，得到較為可靠的用戶最近鄰居集合進而計算預測評分，并將評分從大到小的前N個推薦給用戶。置信度可以避免兩個用戶共同評分項目很少時所帶來的虛假相似現象，用戶特征可以避免新用戶因沒有歷史數據所造成的推薦質量較低的問題。

1 基礎協同過濾算法

推薦算法一般包括三步：建立用戶模型、尋找最近鄰居和產生推薦[6]。

1.1 用戶模型的建立

用戶對項目的評分信息一般用R表示，R是一個m×n的矩陣。m表示用戶的數量，n表示項目的數量，Rij表示用戶i對項目j的評分。評分在[1～5]之間，用戶的喜好程度與評分大小成正比。

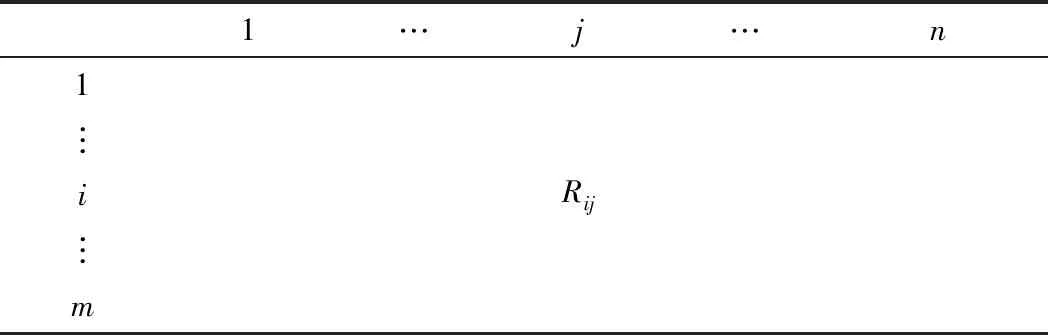
表1 用戶評分矩陣

1.2 尋找最近鄰居集合

目標用戶的最近鄰居通過相似度計算來尋找，相似度越大說明兩用戶之間越相似。最常用的相似度計算方法有皮爾遜(Pearson)相關系數、余弦(Cosine)相似度和修正的余弦(Adjust Cosine)相似度[7]。

(1) 皮爾遜(Pearson)相關系數：首先會找出兩位用戶都曾評論過的項目，然后計算兩者的評分總和與平方和，并求得評分的乘積之和。

(1)

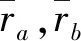
(2) 余弦(Cosine)相似度：用向量空間中兩個向量夾角的余弦值作為衡量兩個個體間差異的大小的度量。

(2)

式中，rai、rbi分別為用戶a和用戶b對項目i的打分；simcos(a,b)為兩用戶的余弦相似度。

(3) 修正的余弦(Adjust Cosine)相似度:考慮到每個用戶打分時都打分習慣的影響，經用戶的評分去掉用戶的平均評分來均衡用戶的評分差異。

(3)

式中，rbi為用戶b在項目i上評論分數；Ia、Ib分別為兩用戶各自評論的項目集合；sima-cos(a,b)為用戶間調整的余弦相關性。

1.3 產生推薦

用以上任一種相似度計算方法進行計算，獲取最近鄰居集合之后，利用式(4)對用戶沒有打分的項目進行預測打分，并將預測分數從大到小取前N個推薦給目標用戶。

(4)

式中，Ua為目標用戶a的最近鄰居集合；sim(a,b)為皮爾遜相關系數；prea,i為目標用戶a對沒有打分的任一項目i的預測打分。

2 算法改進

2.1 基于置信度的相似度計算

并不是用戶對所有的項目都進行評分，由于不同用戶的不同的興趣愛好，所以用戶的打分項目各種各樣，所得到的用戶評分矩陣稀疏度很大。在獲取用戶最近鄰居集合的時候，無法反映用戶的相似喜好，尤其是兩個用戶共同評價的項目只有一個的情況下，他們的相似度很高[8]。

因此，在計算用戶相似度時需要有一個置信度，本文將Jaccard函數[9]作為置信度的度量函數，公式如下：

(5)

式中,I(a)、I(b)分別為用戶a和用戶b各自打分的項目集合；|I(a)∩I(b)|為兩用戶打分項目的交集數量；|I(a)∪I(b)|為兩用戶打分項目的總數量。

將式(5)引入到相似性計算公式(1)中，得到一個改進的相似性度量公式，如下：

(6)

式中，S(a,b)為相似置信度。simi(a,b)在一定程度上緩解了兩用戶共同打分項目少時造成的相似虛假現象，提高了推薦的質量。

2.2 基于用戶特征的相似度計算

用戶一般擁有用戶編號、年齡、性別、職業、郵編等基本的信息。這些基本特征在一定程度上會影響著用戶的興趣喜好，擁有相同特征的用戶可能會是相似用戶。這些信息可以分為三類：① 年齡；② 性別；③ 職業和郵編。在新用戶來臨沒有歷史數據的情況下，用戶特征顯得尤為重要，所以將用戶的基本特征引入到相似度的計算中，可以避免用戶冷啟動所帶來的推薦效果不好的問題。

(1) 用戶年齡特征。不同年齡的人喜好會有所不同，比如兒童喜歡動畫片，少年喜歡青春偶像劇，老年人喜歡經典影視。兩用戶的年齡差距越小，其喜好相似性越大，超出一定范圍時相似度受年齡的影響微弱。本文中將這一范圍定為10，年齡特征的相似度計算如下：

(7)

式中,UAa、UAb分別為目標用戶a和相似用戶b各自的年齡；simage(a,b)為兩用戶的年齡相似度。

(2) 用戶性別特征。性別相同的用戶喜好一般會相同，如女性比較喜歡化妝品，男性比較喜歡汽車等。性別的取值只有兩個，所以性別特征的相似計算公式如下：

(8)

式中,Sa、Sb分別為用戶a和用戶b各自的性別；simsex(a,b)為用戶間性別的相似度。

(3) 用戶標稱特征。有相同職業的人可能有相同的喜好，如學生常看書籍，醫生常看病例等；有相同郵編的人說明所處地區相同，他們可能會對該區域內的一些東西感興趣。對用戶的標稱特征的相似計算公式如下：

(9)

式中，n為兩用戶間相同標稱特征的數量；m為用戶標稱特征的總數量；simother(a,b)為標稱特征的相似程度。

通過上述所得的各種特征的相似性可以用公式(10)計算用戶a和用戶b在用戶特征上的整體相似度。

(10)

式中,c為用戶特征的分類數；sima(a,b)為用戶特征的整體相似度。本文按用戶各類特征所占比例相同計算。

2.3 基于最終相似度的推薦

改進的相似度計算能夠應對數據稀疏性和用戶冷啟動，把基于用戶特征的相似計算公式與基于置信度的相似計算公式進行結合：先計算基于用戶特征的相似度；再計算基于置信度的相似度；最后將單獨計算所得的兩個相似度按照前者w的比重，后者(1-w)的比重進行相加得到最終的相似度。相似計算公式如下：

Fsim(a,b)=wsima(a,b)+(1-w)simi(a,b)

(11)

式中,Fsim(a,b)為用戶的整體相似度。整體相似度越高，說明兩用戶越相似，喜好也越接近，推薦給目標用戶的結果也更符合用戶的需求。

2.4 改進的算法描述

Input:用戶評分矩陣Rm×n，用戶特征信息，最近鄰居數K，目標用戶a。

Output:目標用戶a的Top-N推薦集。

① 將用戶評分信息轉化為用戶評分矩陣Rm×n，利用式(6)計算用戶間的相似程度，獲得simi；

② 利用用戶特征信息，獲取用戶的各類特征，并分別計算用戶間的年齡相似程度simage，性別相似性simsex，標稱特征相似程度simother；

③ 將所得的各類特征相似程度代入到式(10)中，從而獲得用戶特征的整體相似程度sima；

④ 把第①步所得的結果和第③步所得結果利用式(11)進行計算，取得最終用戶相似度，并得到目標用戶a的最近鄰居集合Ua；

⑤ 根據目標用戶a的最近鄰居集合Ua和式(4)對未打分的項目進行預測打分，對分數從大到小排序，形成Top-N集合進行推薦。

2.5 算法分析

本文的相似度算法與傳統的相似度算法(余弦相似度)復雜度都為O(n2)。本文中每兩個用戶特征總相似度計算需2次加法，一次除法，開銷很小；計算置信度相似度計算時，在Pearson相關系數計算公式之后乘以一個置信度。而文獻[5]在計算相似度時，在Pearson相關系數計算公式中為每個項目增加權值。兩相比較知本文算法的開銷小于文獻[5]中算法的開銷。

3 實驗結果及分析

3.1 實驗數據

實驗選取的MovieLens數據集，是由GroupLens研究小組在明尼蘇達大學研究項目上收集的。其中包括943個用戶對1682部電影的100000條評分記錄[10]。用戶的打分最低為1，最高為5，所打的分數與用戶的喜歡程度成正比。根據數據稀疏性公式可以計算該數據集的數據稀疏度[11]。

(12)

式中,Spa為數據集的稀疏程度；num為打分總數量；m為用戶的數量；n為項目的數量。用式(12)計算得到該數據集的稀疏程度為93.69%。

3.2 評測標準

推薦系統準確性測量分為3類：預測準確測量(如MAE、RMSE)、分類準確測量(如ROC曲線)和排序準確測量[12]。本文采用平均絕對誤差(Mean Absolute Error，MAE)作為度量標準，MAE的定義如下[13]

(13)

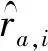
3.3 實驗結果分析

在數據集中給出了5個訓練集(u1.base，u2.base，u3.base，u4.base，u5.base)和5個測試集(u1.test，u2.test，u3.test，u4.test，u5.test)。隨機選取一個訓練集和與其相對應的測試集進行實驗。

改進的相似度計算是由基于置信度的相似計算公式與基于用戶特征的相似計算公式用一個因子w進行結合得到的。對于新用戶而言，沒有歷史數據作為推薦的依據，此時用戶的特征起到主要作用；對于老用戶而言，大量的歷史數據可以為用戶提供充足的依據，此時用戶的特征作用會有所減小，所以理論上w取值在0～0.5之間。下面由實驗進一步來確定w的最佳取值。

w的值從0開始取間隔為0.1，到1為止，w=0表示相似性計算公式中只有置信度，w=1表示相似性計算公式中只有用戶特征，不同w的取值所得的MAE值結果如圖1所示。從圖1可以看出w在取0.1時，MAE取值最小，算法效果最好。

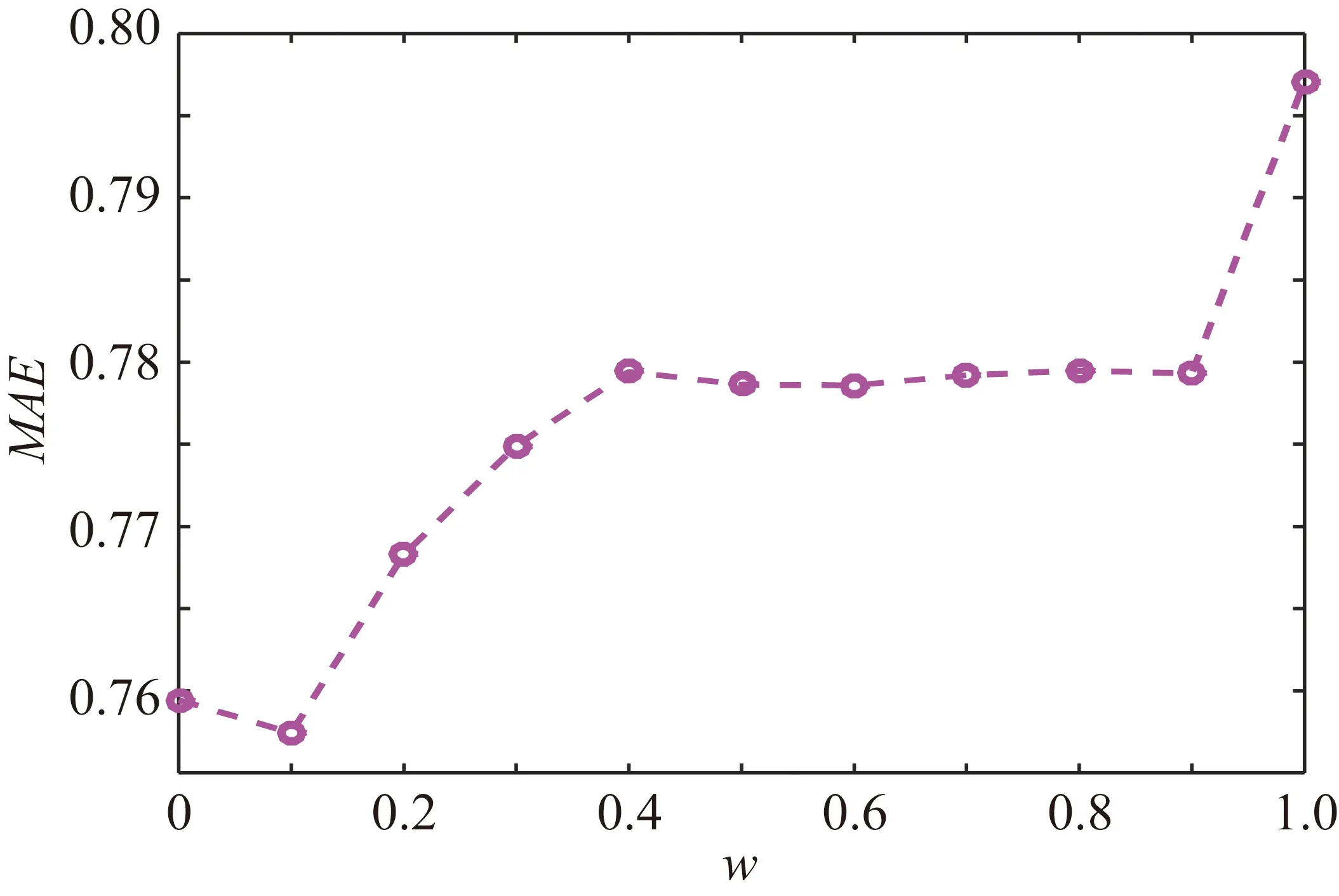
圖1 不同w的取值與所得MAE

目標用戶的最近鄰居數的不同取值對MAE也有一定的影響，最近鄰居數越小，用戶冷啟動的可能性越大。利用上述實驗所得結果，將w的值定為0.1，最近鄰居數從10開始間隔為10直到100為止，計算不同鄰居數下的MAE值大小，結果如圖2所示。從圖2中可以知道用戶最近鄰居數最小時MAE取值最小，這就說明改進的協同過濾算法的推薦質量在用戶冷啟動時有所提高。

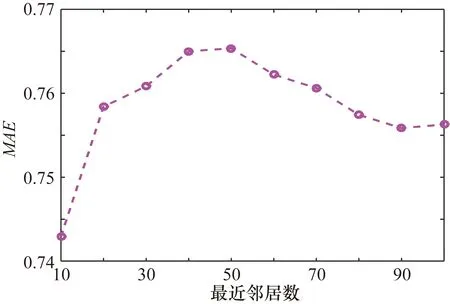
圖2 不同最近鄰居數下的MAE取值

為更好地體現改進的協同過濾算法的效果，將本文的改進算法(ASCCF)與傳統的協同過濾算法(修正余弦相似度)和文獻[5]的改進算法相比較。用戶最近鄰居數從10開始間隔為10依次增加到100 為止，比較不同鄰居數量下各自算法的MAE取值。所得的實驗結果如圖3所示。從圖3可知，最近鄰居很少時本文的算法結果最好，隨著最近鄰居數量的增加，本文改進的協同過濾算法所得的MAE值雖然有所增大，在70點處與文獻[5]相同，80點處比文獻[5]好，最近鄰居數大于85時稍遜色與文獻[5]，但依然比傳統算法的MAE值小，所以本文改進的算法更適用于最近鄰居數小的情況。

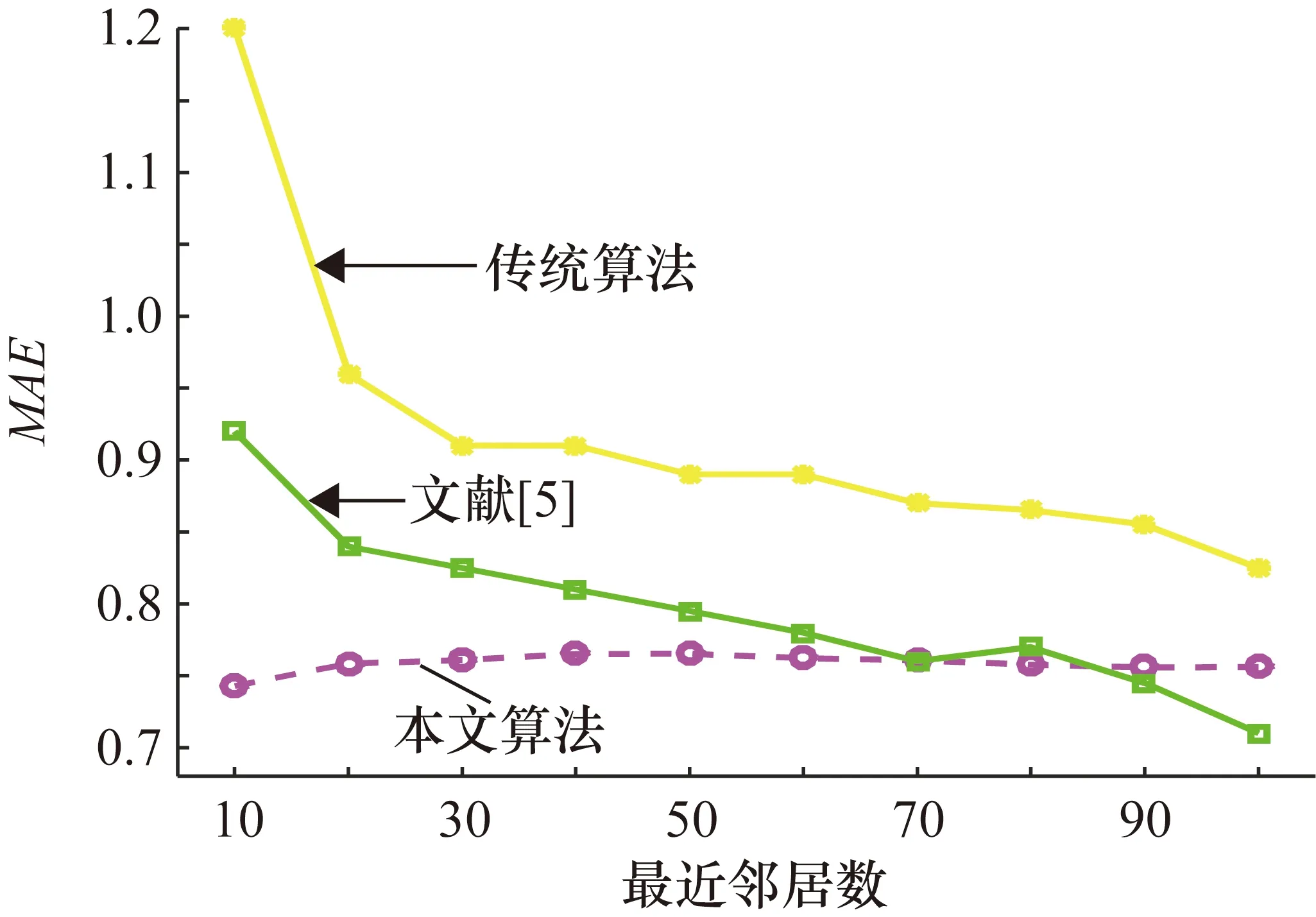
圖3 3種方法的比較

4 結束語

本文針對算法中存在的數據稀疏和用戶冷啟動問題，對最初的傳統過濾算法進行改進，提出一種基于用戶特征與相似置信度的協同過濾算法。置信度的引入讓兩用戶在共有打分項目較少情況下，減少了兩用戶間相似的假象，用戶相似度得到保證進而提高了推薦的準確性。用戶特征的加入，讓新用戶通過自身特征計算用戶間的相似程度，避免了冷啟動所帶來的困擾，進而保證了推薦的質量。再用一個因子將兩種相似度計算方法聯系起來，控制各自所占比重計算用戶間最終相似程度，獲取目標用戶的K個最近鄰居集進行預測打分，按照打分的高低形成Top-N推薦給目標用戶。實驗表明，在評分矩陣稀疏和冷啟動的情況下，本文改進的算法效果很好。但沒有考慮用戶的興趣會隨時間的變遷而發生變化，在最近鄰居數越大的情況下算法也有待改進，因此考慮用戶興趣的時間有效性和在較大最近鄰居數下提高推薦質量將是本文的下一步研究。