基于CW測試的改進Lee室內模型的研究

12 李 帥12 王逸軒

(1.蘭州交通大學 電子與信息工程學院，甘肅 蘭州 730070； 2.甘肅省無線電監測及定位行業技術中心，甘肅 蘭州 730070；3.甘肅省高精度北斗定位技術工程實驗室，甘肅 蘭州 730070)

信息時代的到來，給無線通信網絡帶來了極大的挑戰[1-2]。移動終端和數據流量的爆炸式增長和業務類型的演進更加劇了無線通信網絡規劃和優化的難度[2]。同時隨著無線通信技術的迅猛發展，室內預測模型的應用也愈加廣泛[3]。室內預測模型的最終目的是確保需求區域足夠的信號覆蓋，并能夠方便小型基站或監測站的合理選址[4]。因此，模型的精準化變得十分必要。然而由于室內環境的復雜性，經驗模型即使較為準確，也達不到很高的精度，所以需要經驗模型做出改進才能夠滿足精度上的要求。

現有的室內模型都存在各自的不足，或是精度較低，或是計算耗費時間長，或是適應性不強[5-8]。而Lee模型根據收發天線之間的不同距離，在自由空間損耗模型上添加不同情形計算公式，與其他模型相比，復雜度不高且適用各類場景，經過驗證其準確度較高[1,9]。本文對Lee模型進行了建模以及仿真，通過實際房屋的平面建模，驗證了其準確性，并且在比較了不同擬合方法后，對近中心距離做出了進一步的劃分，添加穿墻情形對應的修正項使得模型更為精準。

1 Lee室內模型

Lee室內預測模型是適用于預測建筑物內部的無線傳播損耗的模型，其核心思想是將路徑損耗的預測分為不同建筑物環境下的幾種情況。該模型定義了近中心距離Dc且認為近中心距離只與天線高度及穿透性值εr有關，而與頻率無關。通過大量的實際數據的測量，針對不同的建筑物情形，Lee模型具有相對應的經驗公式。單樓層模型包括兩種情形：視距(LOS)和非視距(NLOS)情形，其中視距是指接收端位于發射端的直接可視距離之內。其路徑損耗為

(1)

式中，λ為信號波長，d1為近中心距離Dc內的距離。

而近中心距離定義為

(2)

式中，ha和hm分別是基站和移動端天線高度。近中心距離Dc的推導是基于雙射線模型得出的[1,10]。

那么接收端的總功率Pr為

Pr=Pt+Gt-LLOS+Gr

(3)

式中，Pt為發射功率；Gt為發射天線增益；Gr為接收天線增益。

當接收端與發射端距離是不直接可視，即有遮擋物存在。或者距離較遠，即位于近中心區之外甚至建筑物之外時，路徑損耗是3種不同的計算方法。

① 當一堵墻阻擋了發射端和接收端時，其路徑損耗為

(4)

其中，FLOS為由于在天線與近場距離之間缺少近中心空隙產生的損耗，

(5)

式中，B為阻擋物厚度(ft)。

② 當接收端位于近中心區之外時，其路徑損耗為LLOS+Lroom，接收端的預測接收功率則為

Pr=Pt+Gt-LLOS-Lroom+Gr

(6)

③ 當接收端位于建筑物之外時，預測接收功率為

Pr=Pt+Gt-LLOS-Lroom-Loutside+Gr

(7)

對于在模型的優化時擬合方法的選擇，主要考慮和比較了4種方法，即最小二乘法、平滑樣條法、線性插值法和線性擬合法。

① 最小二乘法。最小二乘法[11]是最為基礎的擬合方法，其核心思想應用在模型校正中即是求AX=B最小二乘解的問題。A是模型輸入變量的系數，變量如頻率、距離等；B則是實測路徑損耗值。

(8)

式中，{φj(x)}為已知的線性無關函數系，求得系數aj使得上式極小的問題稱為最小二乘問題。

② 平滑樣條法。平滑樣條法[5,12]是對所得接收信號電平或路徑損耗散點值的平滑處理，由于測試時噪聲干擾等不確定因素的影響，損耗值會出現明顯錯誤點，此時運用平滑樣條法就能去除這些點。

③ 線性插值法。線性插值法的主要原理是已知信號強度與距離測量對，估計未知距離對應的強度值。插值是在原來的數據散點之間按照一定的關系插入更多新的點，這樣可以方便找出數據的變化規律。平滑樣條和線性插值法一樣都是非參數擬合。

④ 線性擬合法。最小二乘法是線性擬合中的一種。線性擬合的一般原理是找到最為逼近原始數據的形如y=f(x,b)的表達式。求出函數關系，如果未知參數b是線性的，則模型是線性的。

2 測試方法與過程

為了驗證Lee模型的準確性，將圖1所示房間作為測試的場所，選取走廊為視距情形，測試室至走廊以及辦公室至走廊為穿墻情形，進行了大量測試。同時還需要對房間環境建模以方便模型環境信息的提取。

2.1 測試設備

測試主要設備包括：AV1485射頻合成信號發生器、便攜式頻譜儀、矢量網絡分析儀、ICOM AH-8000、0 dB增益天線、拉桿天線及支架、5D-FB饋線、各種TNC/SMA轉接頭等。

2.2 測試場所的測量和繪制

首先對實驗室進行精確測量，繪制包括各房間布局、墻體、門等。見圖1。

圖1 測試場所平面圖

2.3 模型的驗證

分別對視距和非視距兩種情形做了驗證測試。視距情況時在走廊選擇相距3 m、5 m、7 m的三組收發端，并根據天線的適用發射頻率范圍選取902～926 MHz頻段，以4 MHz為步進來進行點進式測量，用得到的數據與經驗公式計算出的數據作對比，發現得到的誤差不超過10 dB。見圖2。

非視距情況時在走廊和測試室利用矢量網絡分析儀依據不同距離從800～3300 MHz頻段做掃頻，得到的損耗與實際差值最多可達25 dB。圖3以兩組距離，分別是2.7 m和5 m為例。

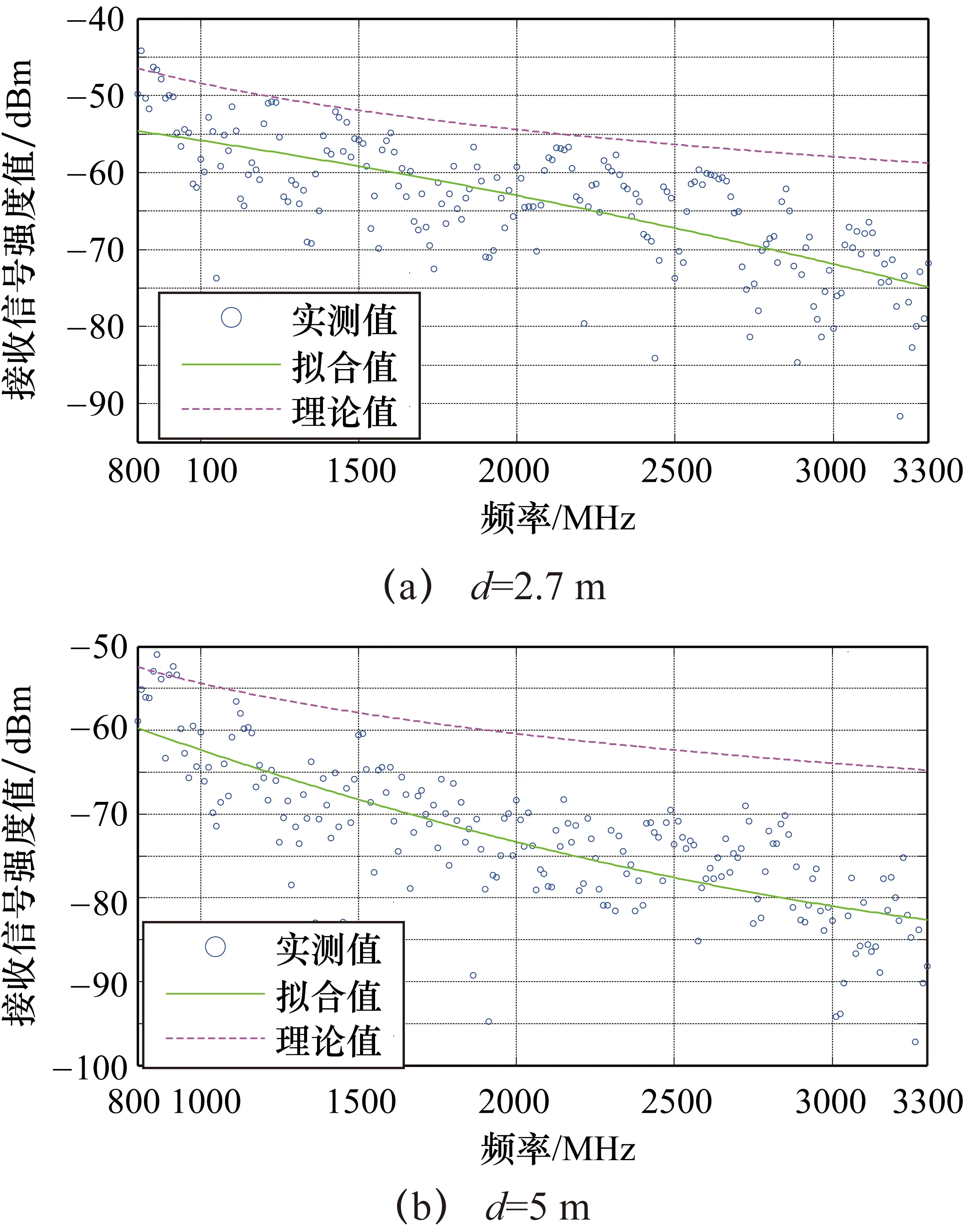
圖3 非視距測量結果

2.4 模型的優化

通過驗證測試發現Lee模型較為符合實際環境。但在非視距情況時由于電磁波傳播是有阻擋的，使得NLOS情形變得更復雜，且增加了影響因素，預測模型與實際環境還是存在較大的差距。在傳播模型的優過程中，大量而又準確的測量數據是得到與實際場景相吻合的傳播模型的前提。因此，由Lee提出的CW測試原則[13-15]，即在測試信號的40個波長內必須滿足有36～50個采樣點，使得校正后的傳播模型滿足保留慢衰落，平滑快衰落的要求。為滿足此原則，設定從直線距離穿過墻體(即墻體與收發端成90°)以5°步進到150°的不同距離值(即將近中心距離分段)，分三組共39個測試點，每個點做三次掃描平均，再次測試得到收發端有一堵墻隔擋的損耗情形。此次測試使用拉桿天線來避免全向天線可能造成的接收端位置不確定問題。使用平滑樣條擬合去掉較為明顯的噪聲或設備影響產生的干擾點，圖4顯示拉桿天線駐波比SWR(Standing-Wave Ratio)較高和較低的幾個頻點的結果。

從圖4的結果可以看出當加上與理論值相差的恒定25 dBm損耗值后，Lee模型的理論曲線與實測值平滑樣條擬合后的曲線基本相符合。產生這種情況的原因可能有三種：

① 設備原因，由于拉桿天線在高頻段的性能較差以及饋線的彎曲程度較大，出現了粗大誤差。

② 人為原因，在實驗時由于測試人員在周圍走動的干擾造成損耗值增大。

③ 場景因素，墻壁上的鐵質掛件，會影響電磁波的傳播。

為了減小Lee預測模型與實際應用到場景時的誤差，最終采用平滑樣條和線性擬合的方法對模型優化。

Lee模型中當有一堵墻阻擋收發兩端時，預測的損耗實際上是自由空間損耗加上阻擋物厚度(即墻厚)的損耗。由于墻厚一般在20 cm左右，而當天線高度和地板材質確定時，近中心距離也是不變的，所以可以把阻擋物損耗看作一個常數C。測試時采用的CW測試所發射的信號頻率是已知且固定的，所以自變量只有距離lg(d)，用X表示，其系數表示為A，自然式(4)可以改寫成：

(9)

發射0 dBm功率、2.4 GHz頻率的信號，兩天線高度總和為2.23 m，木地板的εr值為3，近中心距離為3.86 m，依舊以角度選定測量點，每個點還是做三次測量并將所得值平均，對得到數據先做預處理，即平滑各散點并繪制曲線，考慮天線增益，饋線損耗以及駐波比換算出的反射率，利用線性擬合方法求出A、C值，那么式(9)變為

LLOS=17.06×lg(100×d)+35

(10)

式(10)就是最終對Lee模型在穿墻情形下的修正公式。圖5是修正模型與原模型在實測數據下的吻合度對比。

通過原模型和改進模型的對比可以明顯看出：改進模型消除了Lee模型應用到實際穿墻場景時的粗大誤差(25 dB)，實測數據與改進模型的均方根誤差RMSE為1.4842(<8 dB)，符合模型校正結果分析判別準則。

圖4 網格化測量結果

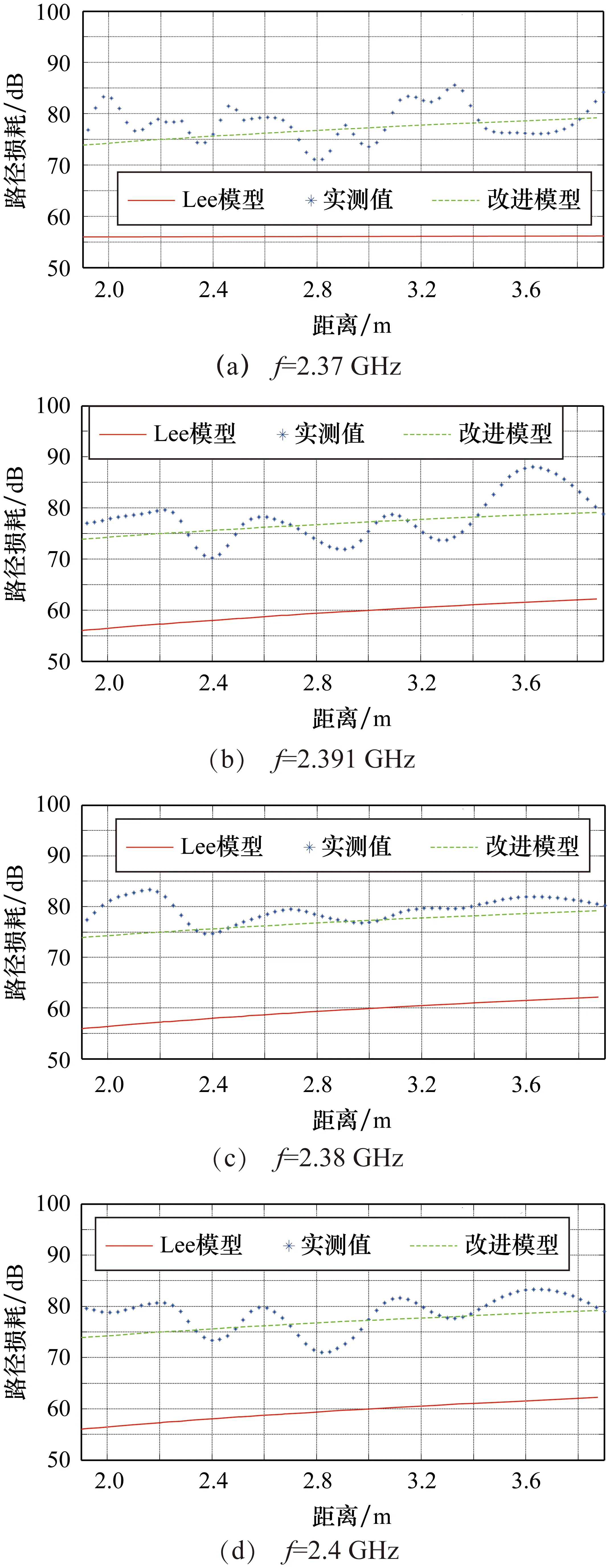
圖5 改進模型與原模型對比結果

為進一步驗證改進模型的準確性，進行其他實際場景的測試。辦公室和走廊之間間隔一堵墻，設置頻率為800～3300 MHz，距離分別是5 m和2 m，使用相同的設備得到穿墻的測量結果，如圖6所示。

從圖6可以看出改進模型很好地與實測數據吻合，說明改進模型對不同的實際場景有較強的適應性。

3 結束語

模型針對于收發兩端間隔一堵墻、天線位置較低、高頻段、超短距離的特定情形做出了預測模型在實際場景的改進，并實現了較為符合實際測量數據的預測。

圖6 辦公室場景測試結果

改進模型可以準確預測穿墻情形時信號傳播衰減情況，并且不需要輸入太多參數，只需知道收發端的間距。精確度上比原模型提高了近20 dB。除了本文所使用的平滑樣條和線性擬合結合的方法之外，還可以考慮例如大數據、深度學習等方法進行仿真，前提是有足夠多的數據可以作為真值去學習和訓練，從而得到更為準確的預測模型。室內環境是極為復雜的，存在各種各樣的場景，由于經驗模型需根據大量真實房屋建模測試得出一般公式，因此不僅穿過單一墻體的模型需要校正，還需要對多堵墻和人等影響電磁波傳播情況校正，多樣情形的室內傳播模型的校正還需進一步研究。