電動汽車充放電的優化管理

● 劉 洋

一、問題重述

（一）引言

為應對交通領域的石油資源消耗多、溫室氣體排放多的問題，世界各國政府都在積極推廣電動汽車的發展。電動汽車的大規模發展離不開電力系統的支撐，但電動汽車無序充電行為隨機性強、同時率高的特性給配電網帶來負荷峰谷差增大、電壓下降、損耗增加等挑戰。同時，電動汽車作為移動式儲能，在削峰填谷、提供電力系統輔助服務、協同消納新能源等方面有廣闊的應用前景。電動汽車與電網互動（Vehicle to Grid，V2G）作為一種對電動汽車充放電行為優化管理的方式應運而生。

（二） 問題提出

根據題目及提供的相關數據，解決如下問題：

第一，根據某城市100輛電動汽車一周的充電記錄，分析電動汽車充電行為特征量的分布規律，為電動汽車充電行為建模，并計算規模化電動汽車的年用電量。

第二，根據一萬輛車的充電電功率的分布以及問題一所得充電行為規律模型，計算24小時1萬輛車的充電負荷曲線。并分析，在何種充電功率的分布下，既能滿足用戶需求，也能減少設備投資，并可降低電動汽車無序充電負荷的峰谷差。

第三，根據充電需求的記錄和光伏發電功率的分布對充電站進行優化管理，在光伏全額利用和允許棄光的條件下計算24小時內充電站的最大利潤。

第四，根據電網各個物理屬性的限制以及根據不同時段用戶充放電電價，使得電網有功網損最小值并且電動車車主總花費最小。

第五，綜合以上各題對電動汽車、新能源充電站、電網互動之間的關系進行綜合分析，對電動汽車與電網互動的綜合規劃進行分析預測。

二、問題分析

問題一：要求根據大量充電行為記錄，建立充電行為模型，并求規模化電動汽車的年用電量。首先七天100輛車的樣本數據進行預處理。因100輛車各天的充電行為沒有必然的聯系，所以將七天100輛車的樣本數據簡單合并為一天700輛車的樣本數據。假設一輛車三種行為特征量（充電開始時刻、連接時長、充電電量）兩兩相互獨立，互不影響，用MATLAB分別作出三個行為特征量的經驗分布函數圖像，并與泊松分布的分布函數圖像對比。猜測它們均服從泊松分布，再利用K-S檢驗法驗證猜測的正確性，并得到參數。分別寫出三個行為特征量的分布律，再相乘即可得到電動汽車充電行為的規律。該模型可做時間和規模上的推廣，最終只需根據充電電量的分布律，得到規模化電動汽車的年用電量。

問題二：要求計算24小時的充電負荷曲線，并計算不同充電功率等級的比例，使得用戶需求得到滿足，減少設備投資，并降低電動汽車充電負荷的峰谷差。首先，在本題中影響充電負荷曲線的因素有充電功率、充電開始時刻、連接時長，因此根據這三個因素的分布，采用蒙特卡洛模擬的方式，使用MATLAB軟件繪制充電負荷曲線。進而求較優的不同充電功率等級的比例，這是一個目標規劃問題，根據題意只需求出一個滿足要求的比例即可。減少設備投資作為目標函數，即讓投資最小；滿足用戶需求和降低峰谷差作為約束條件；最后檢驗是否滿足題目條件。

問題三：要求計算在不同情況下24小時內最大利潤。首先，對數據進行預處理，根據充電時刻計算在每15分鐘內的需求量。得出結果后就能判斷在此時間段之內是否需要購電或售電。將所有時間段內的利潤進行加和，即得到24小時光伏全額利用可獲得的利潤。此問題為優化問題，以此利潤做目標函數，是否需要購電或售電做約束條件，即可得到最大利潤。對于允許棄光，就是可以將多余的光能棄用，只需在第一問目標函數中去掉向電網售電部分即可得到最大利潤。

問題四：要求對配電網中電動汽車充放電行為優化。首先求電網有功網損最小值，采用動態規劃的方法，對電網進行優化，進而采用分層序列法，將求得的電網有功網損的最小值作為約束，采用線性規劃和蒙特卡洛仿真的方法，最終得到電動車車主總花費最小的充放電行為方案。

問題五：綜合前四問的分析結果和方法，對電動汽車和電網之間信息的相互交流進行分析、綜合評價，在深刻了解電動汽車發展意義的前提下，根據切實的問題結果和分析過程，綜合評價未來電動汽車的發展。

三、基本假設

第一，EV用戶在進行電能交換時無需等待；

第二，電動汽車各天的充電行為沒有必然的聯系；

第三，每一輛電動汽車的充電開始時刻、連接時長、充電電量三個行為特征量兩兩相互獨立，互不影響；

第四，每一輛車在固定時間段內充電功率不變

第五，所有電樁都能正常進行充電

第六，電動汽車電池容量充滿后立刻斷電

四、符號說明

ζ1：充電開始時刻

ζ2：連接時長

ζ3：充電電量

t：（t-1）～ t時刻，i=1，2…

q：（q-1）～ q kWh，m=1，2...

h：（h-1）～h小時，j=1.2.3…

L：24小時充電負荷（kW）

N：車輛總數

Pr：第r級充電功率的平均功率，r=1,2,3

Q1：充電量之和

ai：第i個時間段內的售電電價

ti：第i個時間段內的光伏發電功率

Si：第i個時間段內的需求電量

li：第i個時間段內的購電電價

wi：0-1 變量

五、模型的建立與求解

（一）問題一的建模與解答

要求根據大量充電行為記錄，建立充電行為模型，并求規模化電動汽車的年用電量。

第一，電動汽車充電行為模型的建立

首先將七天100輛車的樣本數據進行預處理。因100輛車各天的充電行為沒有必然的聯系，所以將該樣本數據簡單合并為一天700輛車的樣本數據，并將充電開始時刻的取值轉化為數值型。這就相當于進行了700次試驗，得到的結果記為樣本X。

記充電開始時刻為ζ1、記連接時長為ζ2、記充電電量為ζ3，則（ζ1,ζ2,ζ3）是樣本X上的一個3維隨機變量。為了建立電動汽車充電行為的模型，則需要求出（ζ1,ζ2,ζ3）的聯合分布列［1］。根據獨立性假設，ζ1、ζ2、ζ3兩兩相互獨立，則分別求出ζ1、ζ2、ζ3的邊際分布，相乘后得到聯合分布，進而求得充電行為模型。

對于充電開始時刻ζ1，設k為觀察值，求得ζ1的經驗分布函數其中k不大于樣本X的樣本容量n。根據Glivenko定理可知，用經驗分布來近似理論分別是可行的。利用MATLAB的作圖功能做出的經驗分布函數的圖像，如圖1。

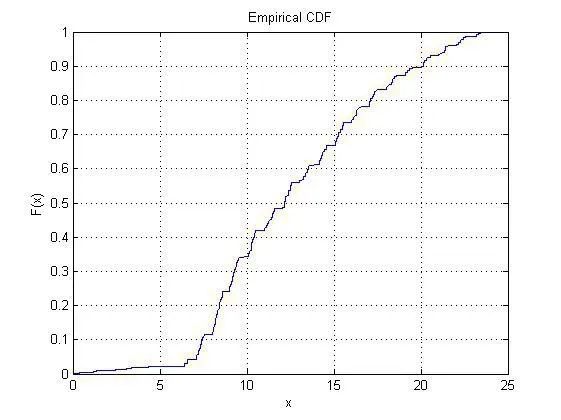
圖 1 ζ1的經驗分布函數圖像

通過圖1觀測出ζ1的經驗分布函數圖像符合泊松分布函數分布圖像的各種特點，推斷ζ1服從泊松分布。進而利用SPSS軟件對猜測進行檢驗，采用K-S檢驗法，檢驗出ζ1服從參數=12.73的泊松分布，檢驗結果如圖4。其中ζ1的分布為

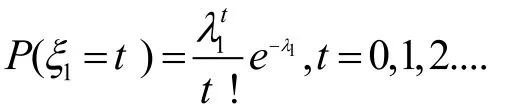
同理，分別對ζ2和ζ3進行以上操作，得出ζ2和ζ3的經驗分布函數圖像，如下圖2和圖3。

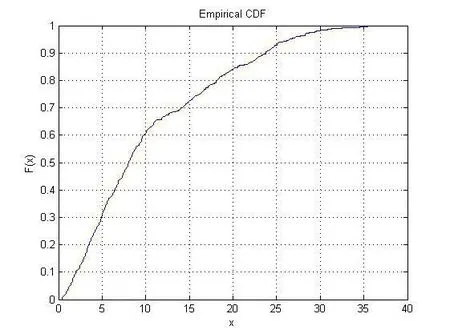
圖 2 ζ2的經驗分布函數圖像

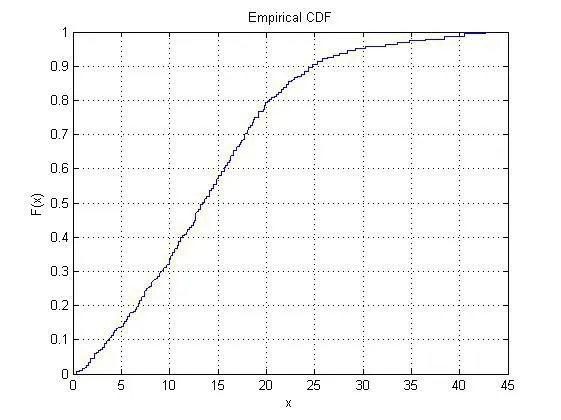
圖 3 ζ3的經驗分布函數圖像

圖 4 K-S檢驗結果圖

得到ζ2和ζ3分別服從λ2=10.60和λ3=14.22的泊松分布，分布分別為

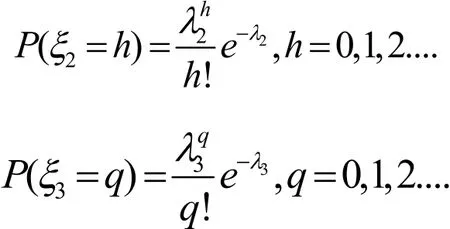
得到電動汽車充電的行為規律為

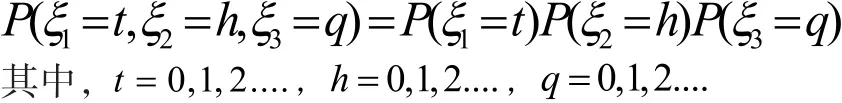
第二，規模化電動汽車的年用電量

求規模化電動汽車年用電量只與1）中充電電量ζ3的分布有關，記N為車輛總數，Q為年用電量

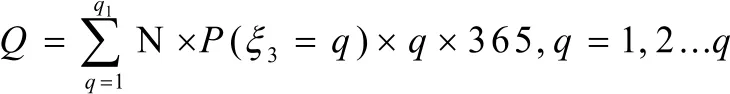
q1為從樣本X觀測出的充電電量的最大值，q1=40。通過MATLAB計算，填寫附表1，如下

附表 1 規模化電動汽車的用電量

通過計算可以發現大約在上午十點大多數車輛開始充電，凌晨零點到六點開始充電最少，主要是因為多數人此時在睡覺。連接時長主要分布在0到10小時之間，這段時間是一般人的休息時間，超過這個時間之后就需繼續工作。充電電量和連接時長的頻率分布類似，主要是因為電動車的充電功率恒定，充電電量也就和充電時長正相關。

（二） 問題二的建模與求解

要求計算24小時的充電負荷曲線，并計算不同充電功率等級的比例，使得用戶需求得到滿足，減少設備投資，并降低電動汽車充電負荷的峰谷差。

第一，計算24小時充電負荷曲線。

充電負荷曲線是指電能用戶的用電設備在某一時刻向電力系統取用的電功率的總和，將24小時平均分為96個時間段，每個時間段的時長為15min。記Lri為在第i時刻以第r級充電功率Nr輛車的充電功率和為車輛數，充電功率等級表如下表1

表 1 電動汽車充電功率等級

第r級充電功率下充電負荷曲線公式［2］為

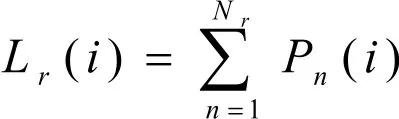
已知采取三個級別的充電功率的汽車比例，記為ωr，其中最終總充電負荷曲線的公式為

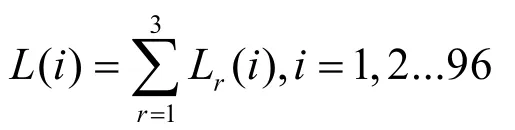
在本題中影響充電負荷曲線的因素有充電功率、充電開始時刻、連接時長，我們已按照充電功率分成三類來計算，因此因素只剩下充電開始時刻T和連接時長Tc。T和Tc對充電負荷的影響為

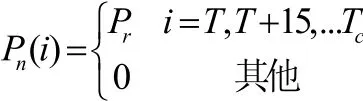
進而使用蒙特卡洛模擬仿真［3］的方法，根據充電開始時刻和連接時長的分布規律，來選取充電開始時刻和連接時長，進而算出充電負荷曲線。

第二，確定較優充電功率等級的比例。

本題為一個目標規劃問題，題意中包含三個要求：滿足用戶需求、減少設備投資、降低充電負荷峰谷差。可將減少設備投資作為目標函數，即

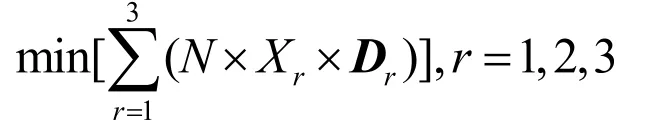
記N為車輛總數1萬輛，Xr為新第r級充電功率等級的比例，Dr為第r級充電功率對應設備的成本。滿足用戶需求作為一個約束，可將該約束簡化為1萬輛車的總需求大于每輛車的平均充電量與1萬輛的乘積，即

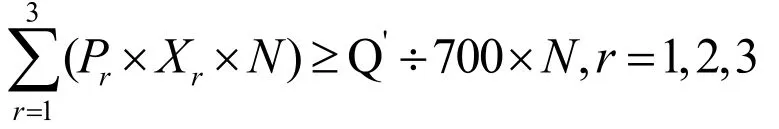
其中Pr為第r級充電功率的平均功率，Q'為充電量之和。

降低峰谷差，我們簡化為降低峰值，根據1萬輛電動汽車的充電負荷曲線，觀測到峰值所在時刻為一天的第900分鐘，即為15點鐘，根據問題一所求充電開始時刻的分布規律，求得時開始充電的車輛數的概率［4］

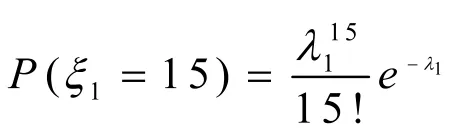
使得在t=15時的充電負荷小于第900分鐘，也就是第i=60個時間段的充電負荷，求得約束

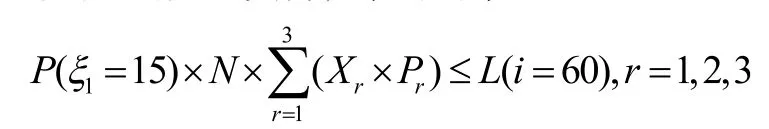
另外有

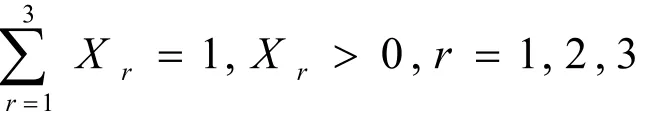
使用lingo求得

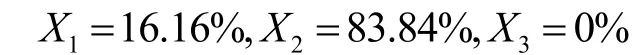
用MATLAB做出在該比例下充電負荷曲線，如下圖6

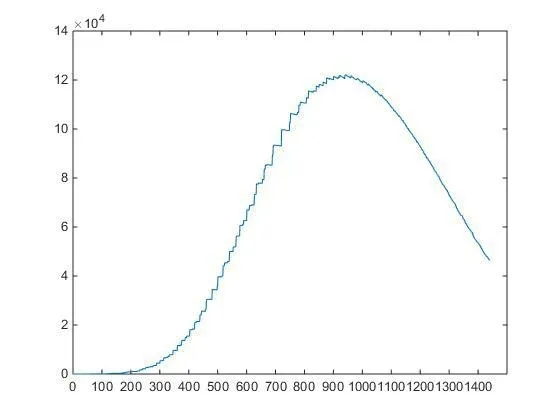
圖 6 改進充電功率比例后的充電負荷曲線

（三）問題三的模型與求解

根據數據列出目標函數和約束條件，用lingo進行求解。

1．數據預處理。要求最大利潤需先知道需求量和光伏發電量的關系，而每15分鐘內的光伏發電量是已知的，就需要求出在此時間段內的需求量即充電電量。

首先在excel中對充電開始時刻進行排序，若該時刻在某一時間段內，則將其對應的電量累加到這一時間段內，直到所有時刻都進行完畢，共得到96組數據。

已知8臺電樁最大功率為50KW，則在15分鐘內的最大充電量為100KWh。若所得結果超過此數值，將其超出部分加到下一時間段內繼續充電。

2．計算光伏全額利用時的最大利潤。由于本題要確定是否需要購電和售電，就要根據發電量和需求量的關系建立一個0-1變量，來確定利潤的組成。

目標函數：

最大利潤=售電電價*剩余電量-購電電價*缺少電量+充電電價*需求電量

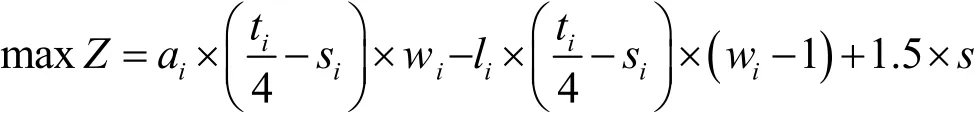
約束條件：

當光伏電量大于需求電量時，0-1變量值為1；當光伏電量小于需求電量時，0-1變量值為0

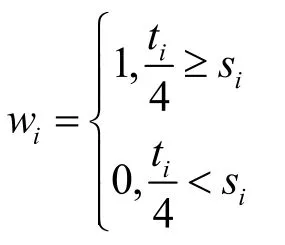
求解結果：最大利潤為1367.527

3．計算允許棄光時的最大利潤。本題與第一問相比只需去掉售出電量所得利潤。

目標函數：

最大利潤= -購電電價*缺少電量+充電電價*需求電量

約束條件：

當光伏電量大于需求電量時，0-1變量值為1；當光伏電量小于需求電量時，0-1變量值為0

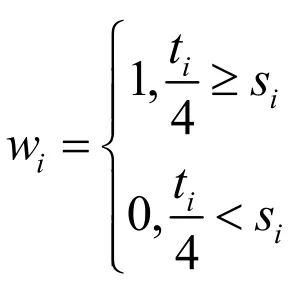
求解結果：最大利潤為1255.355

（四）問題五分析

通過上述分析，使用蒙特卡洛模擬仿真的方法，根據充電開始時刻和連接時長的分布規律，來選取充電開始時刻和連接時長，進而算出充電負荷曲線。進一步調整比例，以降低電動汽車無序充電負荷的峰谷差。利用新能源充電站，通過對不同充電時段劃分進行優化，實現了電動汽車的優化充電；討論光伏的全額利用和允許棄光兩種情況，優化出了24小時充電站的最大利潤。

第三問主要展現了電網與新能源發電站的雙向信息交流，使得充電站根據用戶的需求、不同階段的電價水平、光伏的利用情況與電網進行電量的雙向交流，在合理利用的情況下，使得新能源充電站的利潤達到最高。

由此可見，電動汽車可為電網提供多種改善服務，這些服務主要包括參與系統削峰填谷與新能源發電聯合運行等。

隨著科技的發展，汽車尾氣污染的日益嚴重，電動汽車的將成為一種趨勢，未來將有大量的電動汽車充電站，大量的電動汽車無序接入電網進行充電，將對電網的運行和規劃方面產生較大的影響和改變，根據充電行為對充電負荷曲線進行研究，優化降低峰谷差，對電網的運行狀態有重要意義。新能源充電站在與電網進行聯合規劃時達到盡量大的盈利性，將成為未來新能源發展的極為重要的一部分。

六、模型的評價

模型優點：

第一，利用MATLAB對數據進行處理，并畫出相應圖像，簡單、直接、快捷。

第二，利用蒙特卡洛模擬仿真的方法，對電動汽車的行為進行分析。綜合了各個特征量的分布規律，分析更具客觀性。

第三，對不同時段充電進行優化，根據不同用戶的需求、不同時段的電價水平，實現了新能源充電站電動汽車的優化充電。

模型缺點：

第一，問題一中忽略了連接時長、充電電量之間的相互關系，偏離實際情況。

第二，問題三中約束條件太過于簡化，未能充分反應新能源充電站和電網之間的相互信息傳遞。

七、模型的推廣

仔細分析各題所建模型，對未來電動汽車的發展有良好的輔助作用。聯系電動汽車對電網進行規劃可有助于未來新能源充電站的建立和合理利用。通過減少峰谷差減少電動汽車無序充電對電網的損害，利用優化模型優化出不同條件下的充電站最大利潤，對未來新能源充電站的發展是一大機遇。未來將有大量電動汽車面向社會，根據我國的具體交通數據，通過所建立的無序充電模型，構建出適合我國的無序充電模型，及充電站和電網的交互。