淺談數學情境型試題的命制

沈健

摘要：基于對數學情境的認識，還原2019年蘇州市學業質量監測中兩道小學數學試題（油價上調問題和選購比薩問題）從取材到初稿，再到試測與修改，最后定稿的命制過程，說明數學情境型試題（將數學問題置入某種現實情境中的試題）的命制原則：突出現實性和針對性;體現過程性和導向性;重視開放性和差異性。

關鍵詞：數學情境試題命制學業質量監測

通過學業質量監測了解學生學業水平和綜合素養的發展是國際通行的做法，很多國家和地區都將其作為評價教育質量和促進教育質量提升的重要手段。2019年蘇州市學業質量監測學科工具命制小組提出了“基于課標，關注素養，對接國際，著眼未來”的命題理念，要求兼顧對學生知識、能力和素養的測試。這就對各個學科的試題命制提出了加強情境設計，注重聯系生活實際，考查學生運用所學知識分析問題、解決問題能力的更高要求。

數學情境型試題是指將數學問題置入某種現實情境中的試題。本文嘗試基于對數學情境的認識，還原2019年蘇州市學業質量監測中兩道小學數學試題的命制過程，說明數學情境型試題的命制策略。

一、對數學情境的認識

《義務教育數學課程標準（2011年版）》（以下簡稱《課標》）對數學情境有較充分的闡述，數次提到了“情境”一詞。例如，在“教材編寫建議”中指出：“素材的選用應當充分考慮學生的認知水平和活動經驗。這些素材應當在反映數學本質的前提下盡可能地貼近學生的現實，以利于他們經歷從現實情境中抽象出數學知識與方法的過程。”在“評價建議”中指出：“對基礎知識和基礎技能的考查，要注重考查學生對其中所蘊涵的數學本質的理解，考查學生能否在具體情境中合理應用。”

PISA（Programme?for?International?Student?Assessment）是一個具有廣泛影響的國際學生評估項目。PISA數學學科的設計理念是：一個人的數學素養不僅僅是指學會（理解和掌握）一定的數學知識和技能，更重要的是，能夠在未來的社會中、在各種不同的領域和情境中，提出問題、分析問題和解決問題。因此，PISA的數學題目都具有現實背景。

PISA將數學情境分成個人情境、教育與職業情境、公共情境、科學情境四大類。個人情境與學生個人的日常活動直接相關;教育與職業情境取材于學生的學校生活或工作環境;公共情境要求學生觀察更為廣泛的周邊環境的某些方面;科學情境更加抽象，可能會涉及一個技術過程、理論情境或明確的數學問題。

二、兩道數學情境型試題的命制過程

（一）取材

數學情境型試題可以取材于學習生活或社會生活的焦點或熱點問題，從而在情境中既考查學生通過閱讀梳理條件和問題的能力，又考查學生選擇并提取數學信息的能力，還可以考查學生是否養成認真讀題審題、細心檢查反思的良好習慣。

我們分別從一條新華網的消息和一個網絡段子中摘選了兩個素材。

素材1記者從國家發改委獲悉，12月29日0點，國家上調汽油、柴油限價，汽油每噸上調70元，柴油每噸上調70元。本次調價是年內第十一次上調。本次調價過后，2017年成品油調價將呈現“十一漲六跌八擱淺”的格局。北京市92號汽油價格調至6.84元/升，按一般家用汽車油箱50L容量估測，加滿一箱92號汽油多花約2.5元。下一次調價窗口將在2018年1月13日0時開啟。

2017年油價的第十一次上調雖然不屬于和學生生活有密切聯系的“個人情境”，但是是學生耳聞目染的社會熱點問題，屬于“公共情境”。

素材2今天上午改試卷遲了，食堂沒有吃的了，幾個老師就去沃爾瑪吃比薩。點了一份9寸（直徑）的，結果服務員端來兩份5寸（直徑）的。我們說：“我們點的是9寸的啊！”服務員客氣地說：“9寸的沒有了，所以給你們上了兩份5寸的，不僅價格是9寸的一半，還多送了你們1寸。”于是，我們拉住服務員，好好地給她普及了一下圓的面積的知識：“圓的面積公式是S=πr2。算了一下，9寸的面積約為63.585平方寸，5寸的面積約為19.625平方寸，所以，兩個5寸的面積加起來是39.25平方寸。老實說，給我們三份5寸的，我們還虧著呢！”服務員驚呆了，無語了，最后上了四份5寸的，相當于免費多送了一份。我們都吃得走不動路了。知識就是力量啊！

這一材料的背景，大部分學生都比較熟悉，屬于“個人情境”。由一個場景引出數學知識的應用，通過面積計算實現“劇情反轉”，能夠體現《課標》中“從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律，求出結果并討論結果的意義”的要求。

（二）初稿

根據命題的要求和遴選的素材，我們命制了兩道試題。

試題12017年12月29日，汽油價格出現年內第十一次上調。北京市92號汽油價格調至6.84元/升，按一般家用汽車油箱50?L容量估測，加滿一箱92號汽油多花約2.5元，則油價上調前為元/升。

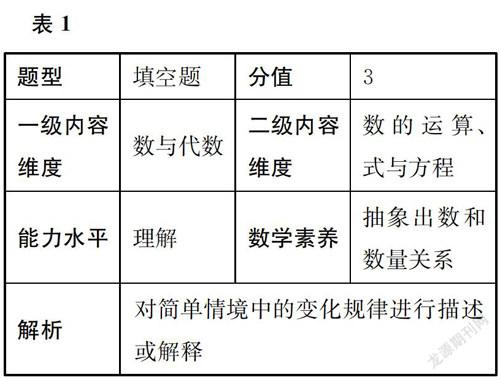
結合監測框架，確定本題的各項指標（見表1）。

本題重點考查學生解決生活中簡單的實際問題的能力，要求學生在讀懂題意的基礎上，抽象出數量關系，即“上調前每升油的價格+每升油上調的價格=現在每升油的價格”和“每升油上調的價格=多花的錢÷加油的量”。求的是上調前的油價，可以用算術和方程兩種方法解決。

試題2一般來說，必勝客普通裝比薩是9寸（直徑）的，大盒裝是12寸的，小盒裝是6寸的，可以滿足不同的需求。小章和小陶去吃比薩，點了一份12寸的。服務員客氣地說：“很抱歉，12寸的賣完了。”同時，端來了一份9寸的和一份6寸的來抵換。小章說可以，“9+6=15（寸），還大了3寸”。小陶說不行，一定要服務員拿一份9寸的加兩份6寸的。你同意誰的觀點？用計算來支持你的看法。

評分標準如下：

12寸面積=36π或113.04，得2分

9寸面積=20.25π或63.585，得2分

6寸面積=9π或28.26，得2分

9寸面積+6寸面積=29.25π<36π，得2分

9寸面積+6寸面積×2=38.25π>36π。得2分

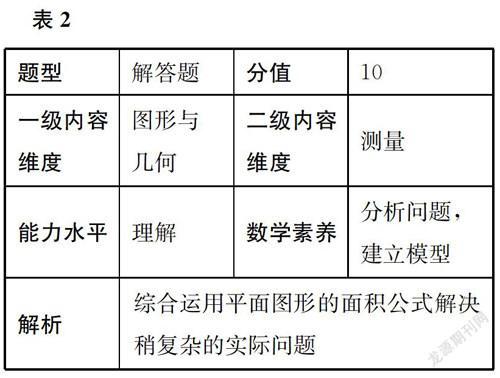
結合監測框架，確定本題的各項指標（見表2）。

本題重點考查學生解決生活中稍復雜的實際問題的能力，要求學生從換比薩情境中抽象出圓的面積問題，即“一個直徑為9的圓和一個直徑為6的圓”與“一個直徑為9的圓和兩個直徑為6的圓”，哪一種組合的面積之和更加接近一個直徑為12的圓的面積——比薩的大小本質上是圓柱的體積，但是由于比薩的厚度大致相同，所以可以轉化成圓的面積來比較。

（三）試測及修改

根據第一輪試測（選取約300名外地學生進行的小規模測試）的數據分析，對兩道試題做進一步修改。

試題1在第一輪試測中得分率為44.9%，表明不少學生無法對這道題正確作答，但是其具體原因可能是多樣的。根據本題的特點，決定將其改為選擇題：相對于填空題而言，選擇題通過設置不同的選項，不僅可以測量學生掌握所學知識的程度，而且可以測量學生對所學知識理解、分析、判斷、應用和綜合的能力;通過對錯誤選項的分析，更便于發現、剖析學生在學習中存在的問題，以更好地指導教學。修改后的試題1如下：

2017年12月29日，汽油價格年內第十一次上調。北京市92號汽油價格調至6.84元/升，按一般家用汽車油箱50升容量估測，加滿一箱92號汽油比上調前多花約2.5元，則油價上調前為（）

A.?6.89元/升B.?6.79元/升

C.?7.34元/升D.?6.34元/升

其中，B為正確選項;錯選選項A表明學生可能審題不清，如理解題中“上調”“調至”“上調前”等關鍵詞的意義出現失誤，導致數量關系分析錯誤;錯選選項C表明學生運算出錯;錯選選項D表明學生不但運算出錯，而且數量關系分析錯誤。

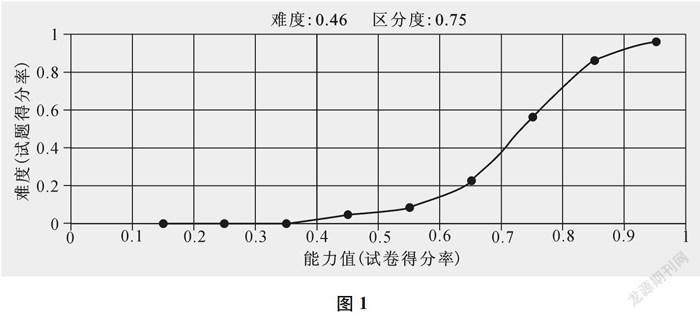
試題2在第一輪試測中得分率為46.0%，有37.19%的學生得滿分，而有47.93%的學生得0分。觀察難度曲線（如圖1），可以看到本題區分度良好，但是能力值較低的學生得分率基本都為0。

《課標》指出：“恰當評價學生在解決問題過程中所表現出的不同水平。”所以針對以上情況，對試題2在兩方面進行修改：（1）修改題干的描述，加上直觀的圖示，使題目更具有生活氣息，從而降低閱讀難度;（2）修改評分標準，使之能將能夠判斷結論但在說明中存在困難的學生區分出來。修改后的試題2如下：

某快餐店一般有直徑為6寸、9寸、12寸幾款厚度大致相同的普通比薩供顧客選擇。小章和小陶去吃比薩，點了一份12寸的。服務員客氣地說：“很抱歉，12寸的賣完了。”同時，端來了一份9寸的和一份6寸的來抵換。

小章說：“可以，9+6=15（寸），還大了3寸。”小陶說：“不行，拿一份9寸的加兩份6寸的，那才差不多。”你同意誰的觀點？用計算來支持你的看法。

評分標準如下：

答：同意小陶的觀點。得1分

12寸面積=36π或113.04，

9寸面積=20.25π或63.585，

6寸面積=9π或28.26，得3分

9寸面積+6寸面積=29.25π<36π，

9寸面積+6寸面積×2=38.25π>36π。得4分

圖1

（四）定稿

經過試測和修改，試題1基本達到設計目標，可以定稿。

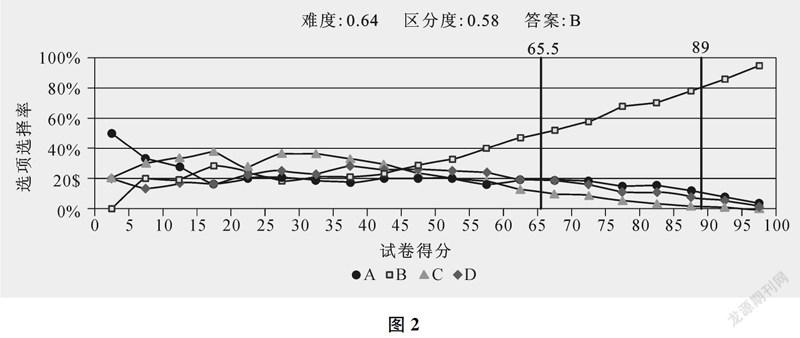
定稿后的試題1在正式測試中的選項分析曲線如圖2所示，表明各個選項都有一定比例的學生選擇，并且選擇情況與學生的數學水平基本一致。

試題2雖然也滿足了命題要求和框架，但是在查看學生的作答時發現了一個問題：部分學生不同意小陶的觀點，理由是3個比薩的面積之和超出了1個12寸比薩的面積，要求店家虧本補貼顯然是不合理的;部分學生同意小陶的觀點，理由是相對而言，3個比薩的面積之和更接近1個12寸比薩的面積。分析這兩種相互矛盾但都有道理的觀點的成因，是對題目中“差不多”三個字理解的歧義。由此造成的解答的多樣化并不體現數學核心素養，也給閱卷帶來了很大的困擾。此外，可將之前的比薩平面圖改為立體圖，使之更加生動形象。因此，對本題做進一步修改：

某快餐店一般有直徑為6寸、8寸、12寸幾款厚度大致相同的普通比薩供顧客選擇。小章和小陶去吃比薩，點了一份12寸的。服務員客氣地說：“很抱歉，12寸的賣完了。”同時，端來了一份8寸的和一份6寸的來抵換。

小章說：“可以，8+6=14（寸），還大了2寸。”小陶說：“不行，拿一份8寸的加兩份6寸的，那才差得不多。”你同意誰的觀點？用計算來支持你的看法。

評分標準如下：

答：同意小陶的觀點。得1分

12寸面積=36π或113.04，

8寸面積=16π或50.24，

6寸面積=9π或28.26，得3分

8寸面積+6寸面積=25π<36π，

8寸面積+6寸面積×2=34π，更接近36π。得4分

將原來的“9寸”改為“8寸”，使得小陶的方案為34π，更接近36π;同時，將原來的“差不多”改為“差得不多”，避免了文字理解的歧義，不會引起考生不必要的猜測和誤解。

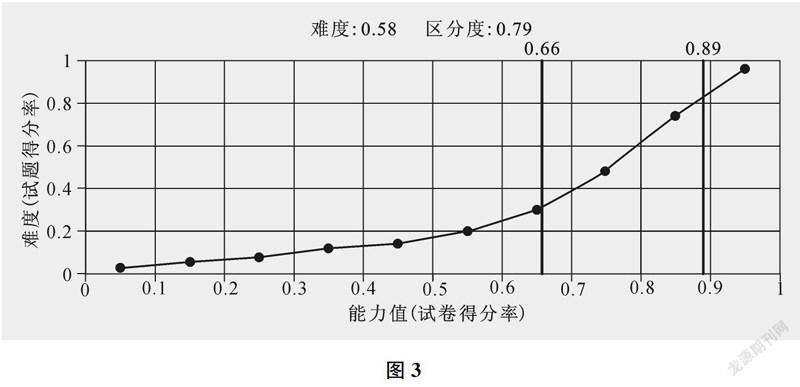
定稿后的試題2在正式測試中的難度曲線如下頁圖3所示，區分度優異，使得各個層次的學生能力均有體現。圖2

圖3

三、數學情境型試題命制的基本原則

（一）突出現實性和針對性

數學知識來源于現實生活，又服務于現實生活。上述兩道試題均選擇了現實生活中的真實素材——油價上漲是學生經常聽說的生活情境，有利于調動學生的生活經驗，并與其數學知識建立聯系;選購比薩是學生日常經歷的生活情境，有利于激發學生的探究興趣，體現學生對具體情境中數學本質的理解和數學知識的運用。在試題信息的選擇上，兩道試題呈現的都是生活中的真實數據，有據可查。考慮到小學生的年齡特點和認知水平，試題2呈現對話情境，配以具有生活氣息的圖片，顯得簡潔、清晰，便于學生閱讀，具有較強的針對性。

（二）體現過程性和導向性

《課標》指出：“在書面測驗中，積極探索可以考查學習過程的試題，了解學生的學習過程。”“評價既要關注學生學習的結果，也要重視學習的過程。”命制數學情境型試題，應該重視過程性和導向性，體現對學生思維過程的考查，方便教師對學生的學習水平做出判斷，從而肯定成績、找出問題，進而引導和改進教學。

例如，上述試題1的不同選項，便考查了學生的不同思維過程。針對學生的不同錯誤，教師可在相關內容的教學中，貫穿“理解題意—分析數量關系—列式解答和檢驗—回顧反思”的策略;關注學生審題能力的提升，如理解題中“上調”“調至”“上調前”等關鍵詞的意義;突出對基本數量關系的分析，即結合題中關鍵詞的意義，找到正確的數量關系。

（三）重視開放性和差異性

數學情境型試題在解題策略和方法上常常能更多地體現開放性：學生通過獨立思考，可以得到不同的解題策略和方法。命制數學情境型試題，應該滿足評價不同思維層次學生的需求，允許不同的學生展現不同的推理、運算等思維過程，讓不同的人在數學考試中展現不同的發展，而不是用程式化的套路題給學生戴上“金箍”。

例如，上述試題2需要學生靈活運用圓柱和圓的相關知識以及轉化的策略，選擇合適的解題方法;還需要學生選擇合理的計算方法，用數據來有理有據地表達觀點，比如用圓周率的近似數3.14進行計算，或者用π來代替，以避免復雜的運算。這些能體現學生在數學素養上的差異。

參考文獻：

[1]?陸璟.PISA測評的理論和實踐[M].上海：華東師范大學出版社，2013.4，6，9，13，30，35，36，41，44，50，56，69-71，81-82，85，88