京都大學行政事務改革的經驗與啟示
顧晟
摘? 要:行政事務改革是京都大學提升事務處理效率,優化行政服務的一項關鍵舉措。改革以破除由日本高校職能內涵擴展、用人經費削減、事務細分化等帶來的學校發展“瓶頸”為背景,其亮點為構建“事務本部-共通事務組織-二級單位事務組織”的三級事務處理體制。這項改革的實踐經驗對我國高校健全和完善提升行政服務效能的制度保障、組織保障、思想保障具有重要借鑒意義。
關鍵詞:高校行政改革;服務效能;事務集約化
中圖分類號:G640? ? ? ? ?文獻標志碼:A? ? ? ? ?文章編號:2096-000X(2019)16-0180-03
Abstract: Administrative reform is a key step of Kyoto University to improve the efficiency of transaction processing and optimizing administrative services. Against the background of breaking the bottleneck for the university resulted from the expansion of functional connotations, cut of personnel expenditure, and segmentation of transactions, the reform highlights the establishment of a three-level transaction processing system of "transaction headquarter - common transaction organization - secondary institutional transaction organization". Practical experiences of this reform is of important referential significance for higher institutions in China to improve the system, organization and ideology assurances for the elevating the efficiency of administrative services.
Keywords: administrative reform of higher institutions; service efficiency; transaction intensification
改革開放以來,我國的綜合國力不斷增強,高等教育規模不斷擴大,育人質量持續提升,科研水平穩步增長,但諸多的體制機制障礙仍制約著高等教育內涵式發展的步伐。傳統管理模式已成為高校進一步發揮人才集中、技術密集優勢,進一步強化立德樹人、科研創新職能的“瓶頸”。如何加快推進“放管服”改革,擴大學校辦學自主權,完善學校內部治理結構,優化學校行政管理模式,健全學校服務保障體系已成為亟需破解的問題。
放眼亞洲近鄰日本,相似的機遇與挑戰同樣推動著日本高校不斷在改革中探索前進。京都大學自2010年起以提升行政事務處理效率、優化行政服務保障體系為目的,研究論證開展行政事務改革的可行性和方法路徑。2012年印發《關于事務改革的思考》[1],集中宣傳改革理念與任務舉措,引導全校師生員工正確理解改革目的,積極配合工作推進。
一、行政事務改革的背景動因
(一)職能內涵擴大使高校事務與日俱增
日本高校承擔的職能內涵正隨著高等教育的發展持續擴大。新型教育研究組織的設立與制度導入、教學科研質量的不斷提升、外部資金與競爭性研究經費的增加、大學評價制度的導入等使日本高校業務日益多樣、日趨復雜。為適應各類資金的增加,日本社會向高校提出了擴大組織機構、統籌內部管理、開展風險管理等新要求,加之伴隨國立大學法人化而來的會計監察制度的施行、戰略目標及計劃的制定、非公務員化后的新型勞動關系處理等多方面因素導致國立大學法人的行政事務工作量與日俱增。
(二)用人經費削減使行政人員數量持續下降
日本十余次的高校人員編制削減與用人總經費改革使行政人員數量持續下降。導入效率化系數后,國家對國立大學法人運營補助金的計算方式發生了改變,其結果是國家對補助金的投入日益減少。另一方面,為應對不斷加劇的少子高齡化問題,確保震災復興資金充足,政府對相應預算的投入持續增長。嚴峻的國家財政迫使日本政府出臺臨時特例法,削減國家公務員薪資。這樣的大環境下,國立大學的運營預算、用人經費(包括人員編制與薪資)面臨著被再度削減的壓力。
(三)事務細分化使人才培養職能受限
設立新型教育研究組織后,京都大學對學校的行政事務組織進行了細分化,小規模事務部大量增加,行政人員個體的工作量與業務類別都有不同程度的增長,超額工作與病休人員數量增多的現象普遍存在,事務處理效率受到嚴重影響,大學的人才培養職能也由此受到制約。
激烈的國際競爭要求日本高校在高等教育的發展道路上不斷追求卓越,為國家建設培養更多的精英人才。
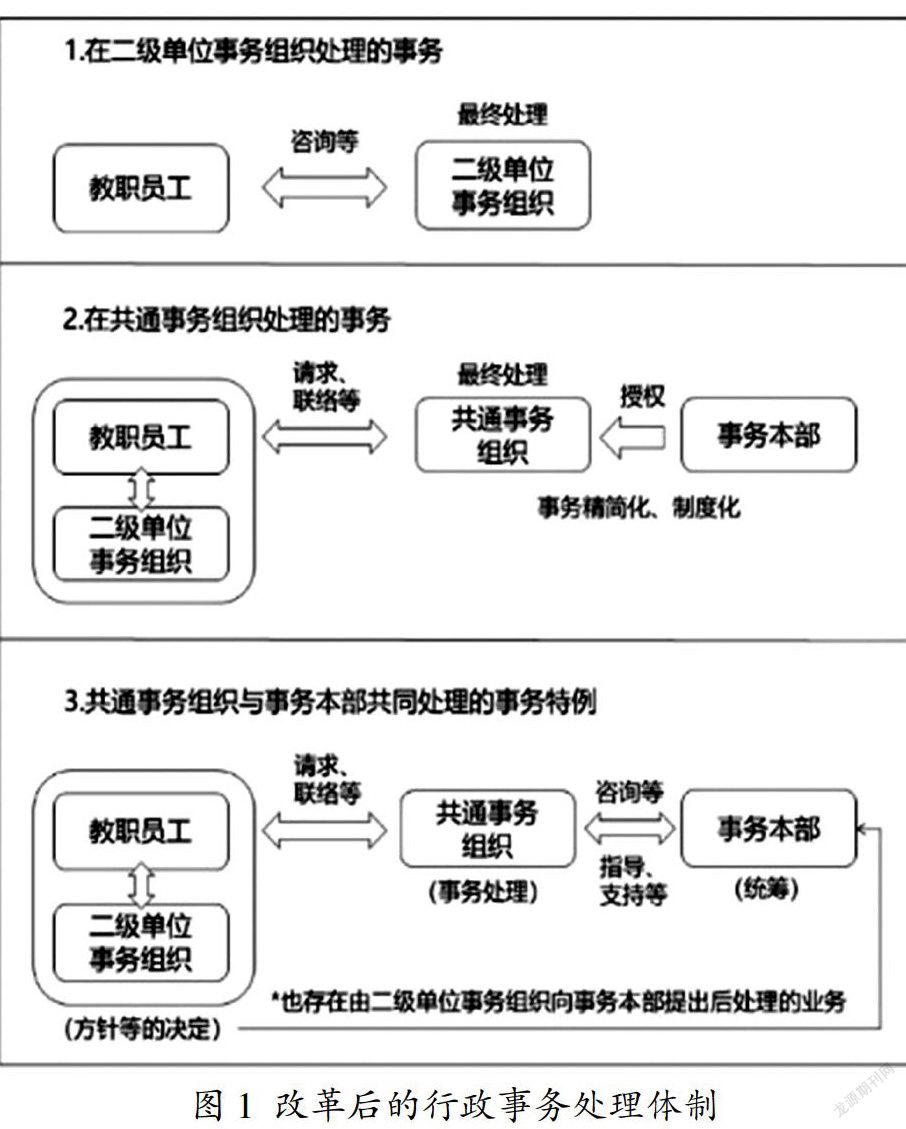
二、構建三級事務處理體制
學校先后多次召集相關職能部門與院系負責人開展座談,廣泛聽取意見,反復論證,對如何提高事務處理效率、優化服務保障體系展開充分探討,耗時兩年最終繪就由事務本部、共通事務組織、二級單位事務組織構成的三級事務處理體制藍圖。各擬建共通事務組織分別設立議事機構和推進機構,確保改革穩步推進,落地落實。改革主要有三項重要舉措:
(一)推進行政事務的效率化和集約化
作為整套改革的基礎,以科學嚴謹的態度對各項行政事務工作的流程與既有事務處理體系進行系統梳理,通過流程重建和系統重構實現事務的效率化與集約化是京都大學行政事務改革的第一步,也是關鍵一步。
推進行政事務效率化、集約化的指導思想主要包含三個方面:第一,為提升事務工作效率,完善事務處理質量,在確保不影響教員教育研究活動的前提下,對總務、財務、設施管理(包括安全衛生)等業務開展集約化改革;第二,對校部機關事務進行重新審視,積極推進授權,為實現“一站式”處理建立快速反應機制并根據需要調整相關人員配置;第三,充分考慮距離條件、國際化、資源共享等因素,確保二級單位各項事務正常運行。
在此框架下,學校對各級行政事務組織負責的范圍進行明確界定。
二級單位事務組織處理單位運營核心業務,如教授會及各委員會運營等總務工作,關于概算及預算事項的決策等財務工作,設施配備計劃等設施安全工作,除學費免除等業務外的教務工作,產官學結合推進規劃制定等研究支持工作,留學交流推進規劃制定等國際交流合作業務。
共通事務組織處理集約化業務,包括常規業務與需要事務本部授權的業務。常規業務有公務出差手續等總務工作,預算執行管理和報告等財務工作,設施運行情況調查等設施安全工作,競爭性科研經費管理等研究支持工作,因公出國手續辦理等國際交流合作業務。需要事務本部授權的業務則有教職員工任免等人事工作,工程執行等設施安全工作,與事務本部學術研究支援室合作推進的研究支持與國際交流合作業務。
事務本部處理需學校統籌協調的業務,但也有部分需事務本部與共通事務組織協作處理的事務特例,如對事故問題的處理處分等總務工作,概算預算賬單制作等財務工作,設施修配計劃制定等設施安全工作,知識產權管理等研究支持工作,國際化人才培養等國際交流合作業務。這些事務特例通常對業務人員的專業要求較高,協作處理時,在共通事務組織內配置專業崗,由事務本部開展指導支持。
建立如圖1所示的三級事務處理體制的同時,京大還設有七大專題部會,每年就總務、財務、教務等專題改革推進情況進行分析總結,設立新課題以推動相關事務效率化、集約化的進一步深入。
(二)設立共通事務組織
這一舉措是京都大學行政事務改革的亮點與核心。共通事務組織設立的指導思想充分考慮了三個方面:第一,行政事務工作量及處理效率方面要適應教職員工人數、學生人數、決算額等現實情況;第二,組織規模方面要充分發揮規模效應;第三,設置時要充分考慮二級單位間的距離、職能、專業領域相關性等因素。
在此框架下,作為京都大學主校區的吉田校區設立了包括本部境內(文科)共通事務部、本部境內(理科)共通事務部、吉田南境內共通事務部、醫學附屬醫院境內共通事務部、西南地區共通事務部、北部境內共通事務部在內的6個共通事務組織;宇治校區設立宇治地區事務部;桂校區設立工學研究科事務部。
本部境內(文科)共通事務部對接文學研究科事務部、法學研究科事務部等9個二級單位事務組織,服務12個二級單位。共通事務部下設總務課和財務課。
本部境內(理科)共通事務部對接能源科學研究科事務部、生命科學研究科事務部等8個二級單位事務組織,服務8個二級單位,同時也向原子爐試驗所事務部提供事務支持。共通事務部下同樣設有總務課和財務課。
吉田南境內共通事務部對接人類與環境學研究科事務部、綜合生存學館事務部等3個二級單位事務組織,服務5個二級單位。共通事務部下設總務課、國際規劃室、財務課和教務課。
醫學與附屬醫院境內共通事務部對接醫學研究科事務部、醫學部附屬醫院事務部共2個二級單位事務組織,服務3個二級單位。共通事務部的下設課室只有財務與研究協助課。
西南地區共通事務部對接藥學研究科事務部、東南亞研究所事務部等6個二級單位事務組織,服務9個二級單位。共通事務部下設總務課、管理課、財務課、西南地區學術研究支援室。
北部境內共通事務部對接理學研究科事務部、農學研究科事務部等5個二級單位事務組織,服務8個二級單位,同時向靈長類研究所提供事務支持與咨詢。共通事務部下設總務課、財務課、設施安全課、研究支援課、教務事務改革室、北部學術研究支援室。
宇治地區事務部與工學研究科事務部分別屬于宇治校區與桂校區,基本保持改革前的組織架構,其定位與吉田校區的6個共通事務組織相同。宇治地區事務部下設總務課、財務課、研究協助課、設施環境課。工學研究科事務部下設總務課、管理課、教務課、學術協助課、財務事務中心。
(三)重構二級單位事務組織與事務本部組織架構
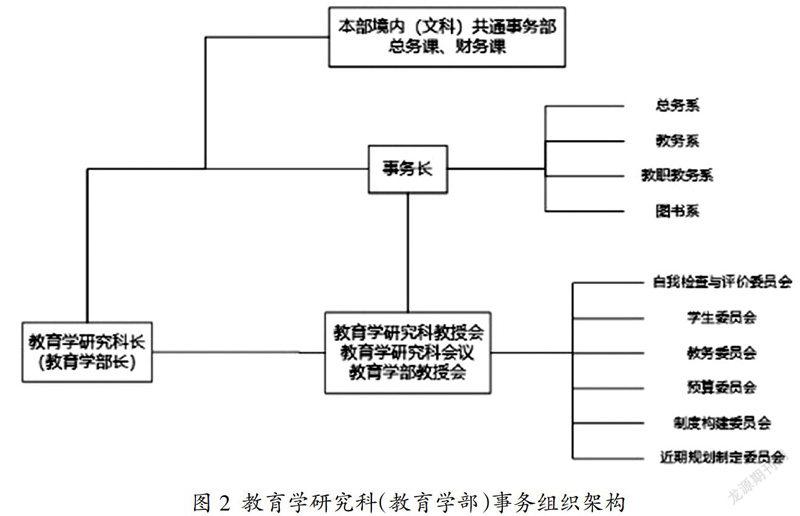
二級單位事務組織設立權主要在二級單位自身,因此相對靈活,組織架構不盡相同。以教育學研究科(教育學部)為例,如圖2所示,其決策機構由教育學研究科教授會、研究科會議、教育學部教授會組成,負責教育學研究科(教育學部)的管理運營。決策機構下還設有自我檢查與評價委員會、學生委員會、教務委員會、預算委員會、制度構建委員會、近期規劃制定委員會。研究科(學部)事務部下設總務系、教務系、教職教務系、圖書系,對接的共通事務組織為本部境內(文科)共通事務部。
同時,為適應三級事務處理體制的需要,進一步推進事務工作的效率化、集約化,更好地發揮事務組織對學校教學科研的服務支撐作用,事務本部也進行了“瘦身”,取消10個中心,變“部-課-中心”三級架構為“部-課”二級架構,最終由“10部24課10中心”變更為“7部25課”。
三、京都大學行政事務改革的啟示
京都大學行政事務改革推進至今,其改革紅利已逐步顯現,其舉措經驗對破除我國高校行政管理體制機制障礙,提升行政服務效能具有一定的借鑒價值:
(一)理清業務流程,明確責任邊界,健全完善行政服務制度保障
理清業務流程是簡化整合行政事務,理順業務鏈運行機制,明確各部門責任邊界,完善制度建設和規范管理的根基。京都大學通過明確事務本部、共通事務組織、二級單位事務組織的職責范圍和三級事務處理體制的運行機制,為整個事務改革打牢了制度基礎和保障。明確責任邊界,既能提高個人和部門的工作責任感,確保工作計劃的順利推進,又能有效防止工作中相互防礙的現象發生,協調相互間的工作關系。這是日本高校保證行政管理高效率的有效方法之一[2]。
(二)開展大部制改革,推進行政事務集約化,完善優化行政服務組織保障
京都大學在充分考慮二級單位間的距離、職能、專業領域相關性等因素的基礎上,建立共通事務組織集中處理相應二級單位的集約化事務可有效提升事務處理效率,減輕事務本部與二級單位事務組織人員的行政負擔。
深度優化高校行政管理結構,大膽創新高校行政管理模式,開展大部制改革,推進行政事務集約化,不僅可提高承接國家“放管服”改革要求的能力,推進行政管理與行政服務的相對分離[3],也可在管理重心逐漸下移至院系的情況下,提升處理共通行政事務的服務能力,為打破學科交叉融合中體制機制的制約提供可行路徑。
(三)加強服務意識,導入內部客戶管理理念,宣貫筑牢行政服務思想保障
服務意識的缺乏在日本高校中并不普遍,行政人員清晰的定位與高校教師較高的社會地位決定了日本高校中不允許也不可能出現行政人員不服從或對抗教師的現象,對學生也以提供方便的態度相待,“官本位”思想幾乎沒有萌芽的可能。在這樣的理念指導下,行政管理部門為學校職能的充分發揮提供了無可替代的服務和支持,大大減輕了教師在行政事務中的負擔[2]。
內部客戶管理理念的導入是有效提升服務意識的可行路徑之一。如每個人員個體或部門能將上下級、業務鏈前后環節等業務提供的對象作為自己的客戶,傾聽客戶需求,完善業務質量,主動提供幫助,行政服務意識在這個過程中就會自然得到提升,優化行政服務的思想保障也由此得以建立。
四、結束語
高校教學科研等職能的發揮離不開行政管理服務的支撐。理清業務流程,明確責任邊界,建立各層級全覆蓋的交流溝通機制,精簡不必要的業務環節,用制度文件將各項業務內容及相應崗位職責予以固化,提高行政工作透明度。在此基礎上,開展大部制改革,提高行政效率,降低行政成本,提高人員素質,加強服務意識。讓教師學者潛心教學科研,將“特事特辦”變為“制度規范”,使為全校師生提供一流服務成為全體行政人員共同的價值追求。用良性的組織管理機制、一流的行政管理服務支撐高校一流建設發展,助推我國向高等教育強國大步邁進。
參考文獻:
[1]事務改革の取組について[EB/OL]. http://www.kyoto-u.ac.jp/static/ja/issue/kouhou/2011.htm#jimukaikaku.
[2]鄭曉齊,孫明.談日本高校行政管理與借鑒[J].外國教育研究,1995(3):19-26.
[3]楊頡.協同治理 協議授權——探索校院二級管理改革新路徑[J].中國高教研究,2017(3):12-16.

