DEA模型在地區對外貿易量分析上的應用分析

李慧慧

摘要：本文提出用于多決策單元（Multiple Decision Unite，MDU）數據包絡分析（l）ata Envclope Analysis，DEA）的一次性模型。假設論域中有多個決策單元，其具體按年度劃分的有多個輸入向量和輸出向量。本文提出的一次性模型可以通過一次建模求解出所有DMU在各個年度中的DEA效率。相對于傳統的DEA模型需要針對每個決策單元和每個年度的單獨建立模型，本文方法具有高集成度和高效率的特點。本文利用MLCap建模語言對提出的一次性模型進行表達，并作為案例將其應用于地區對外貿易量的分析上。算例表明，本文提出的方法在相關研究中具有一定的參考價值。

數據包絡分析（Data Envelopment Analysis），簡稱DEA，是數理經濟學、運籌學、管理科學三者交叉研究的一個領域，曾被廣為研究和使用，目前可以看作是一個成熟的方法。DEA是一種數理方法，用于評價那些能夠用數字表達的多組織（也稱多決策單元，MDU），且每個對象有多輸入、多輸出的績效評價。DEA方法在多組織（多輸入、多輸出）的評價上具有絕對優勢。目前，DEA方法在多個領域的評價分析方面都得到了廣泛的應用[2-4]。在近30年的研究中，DEA方法發展出了多種類型的數學模型，其中線性模型更容易實現大規模求解，多篇文獻[6-7]在DEA研究上也采取線性模型。本文主要針對DEA中C2R對偶輸入模型（即以最小的投入實現指定量的產出）的整數規劃模型改進展開研究。

具體的DEA適用的問題可以被簡單表述為：假設有m個組織（編號：k=l，…，m），每個組織有r項投入（編號：i=l，…，r）.s項產出（編號：j=l，…，s），需要對每個組織的投入/產出效率作出相對評價。方法要求所有的投入和產出都能夠被量化表達，且隱含了對S項產出來說，其值越大越正向影響該組織的效率評價;且對r項投入來說，其值越小則越正向影響該組織的效率。

經典的DEA模型要求針對某個特定組織k分析其DEA效率ek.，將第k（k=l，…，m）個組織的輸入和輸出分別表示為X和y，則模型可以被表達為以下線性規劃模型：

式（1）中的ak是DEA方法引入的決策變量，其含義可以被理解為對組織K’輸入所做的凸組合拆分。求解上式即得到組織K’的DEA效率ek.。若ek.=l，則說組織K’是DEA有效的，或者可以不嚴格地說組織后，的相對效率是l00%。若ek，<1，則說組織K’非DEA有效，或者可以不嚴格地說組織K’的相對效率僅有ek ，XlOO%。

采用式（1）進行分析時，必須對重復m次，即對K’=1，..，，m的每種情況都單獨建模并求解。假設需要評價多年度的相對績效，即當Xki和Yki是分年度給出的若干組數據，則需要更多的模型和求解次數。針對這個問題，本文提出一種可以一次建模并求解出所有DMU在各個年度中DEA效率的方法，并作為案例將其運用于地區對外貿易量的分析上。該方法相比與傳統的模型（1）具有集成度好和效率高的特點。

在其后本文將在第1節中定義多年度多組織的DEA問題，并給出對該問題的一次性模型;在第2節中介紹本文模型基于Leap語言的機器表達方式;第3節給出算例求解和分析;第4節給出本文的結論。

1 問題及模型

1.1 經典DEA問題的一次性求解模型

模型（1）是經典DEA問題常用模型。其缺點是需要對每個組織后’=1，…，m都單獨建立模型并求解，總計建模和求解m次。本文提出使用以下模型完成對經典DEA問題的一次性求解：

式（2）中的變量是DEA方法中的決策變量，其含義可以被理解為對組織k’輸入所做的凸組合拆分。求解模型（2）將一次得到所有組織的DEA效率值ek.（尼’=1，...，m），即有以下簡單定理。

定理1：求解模型（2）將一次得到所有組織的DEA效率值ek，（K’=1，…，m），其結果與多次求解模型（l）所得到的效率值ek，一致。

證明：因模型（2）中每個ek.（K’=1，…，m）所承受的約束互不干擾且等同于模型（1），并且其總體目標是ek.（K’=1，…，m）之和最小，因此模型（2）的ek.（K’=1，¨.，m）最優值與模型（1）的ek.（K’=1，…，m）最優值一致。

1.2 多時間段DEA問題的一次性求解模型

經典的DEA問題只涉及單時間階段數據，即所有DMU的數據都是一個時間階段發生的，問題的要求也是評價該時間階段的相對效率。

本文討論的問題是一個多時間階段的DEA問題：有m個組織（編號：k-l，…，m），每個組織有NI項投入（編號t一1，…，NI）、NO項產出（編號：r一1，-NO），已知各個組織在n個年度的投入數據Xtk（t=1，…，NI，k=l，…，m，i=l，…，n）和產出數據Yrkj（r=1，…，NO，k=l，…，m，j=l，…，n），請相對評價各個年度每個組織的投入/產出效率。

顯然多時間段的DEA問題可以分別針對不同年度多次使用模型（l）或模型（2）完成求解，但是這種方法較為繁瑣。本文提出使用以下模型一次求出各個組織在不同年度的DEA效率值：

一次求解模型（3）與多次求解模型（2）將得到相同的效率值，

其原因在于ek.i（k’=1，…，m，i=l，…，，n）在模型（3）的目標和約束中都是可分解的，且模型（3）所表達的約束與模型（2）所表達的約束一致。

定理2：求解模型（3）將一次得到所有組織在各個年度的DEA效率值ek.i（k’=1，…，m，i=l，…，，z），其結果與多次分別求解模型（l）或模型（2）所得到的效率值ek，，一致。

證明：觀察模型（3）中的任意ek，，，其在目標和約束中均與其他ek。f.（k”≠k’，f’≠i）無關，且任意ek.f所承擔的約束均與模型（2）中的相同，因此上述定理成立。

1.3 一次性求解模型的求解效率問題

注意到模型（3）將比模型（2）和（1）引入更多地變量和約束。一般，具有更多約束和變量的模型在求解時會更困難些。但是對現代數學規劃求解器來說，對大規模模型都會進行模型分解預處理。對這種處理器來說，模型（3）是一個非常容易處理的可分解模型，因此其求解效率基本等同于多次重復求解模型（1）。

2 模型的MLeap表達

為獲得模型（3）的解，需要首先通過一種建模語言將其表達給機器，而后使用求解器得到所需要的結果。本文采用MLeap建模語言實現這一過程。MLeap語言是本文作者所設計的一種數學規劃模型的描述型建模語言。MLeap語言具有很強的描述性（與過程性相對，即不需要任何模型展開和求解過程，只需將模型描述出來即可），基本上只需將數學模型寫成文本形式即可，具體如圖1所示。

和約束段（subject to）的表達方式基本與傳統整數規劃的建模語言相同。不同的是，MLeap建模語言新增了標識符聲明（where），該部分需要明確表明模型中出現的標識符是變量或者常量，并且聲明其數據類型以及范圍。Data部分是MLeap建模語言中的數據表達部分，主要用來對已經聲明的常量進行賦值操作方便計算。MLeap表達中的“一”符號表示換行符，用于連接上一行與下一行的文本內容。

由于模型（3）中的已知常量Xtki和yrkj的賦值矩陣較大，不方便表述，故圖1中Data部分對常量Xtki和yrkj的賦值過程未給出。

3 算例求解與結果分析

為驗證模型的有效性，本文采用國家統計局從2010—2014年分省年度數據帶入模型中進行計算驗證。主要研究各省的各指標對該省的進出口總額（千美元）的相對效率。經過初步的判定，確定影響各省進出口總額的指標有：消費價格指數、消費零售總額、地區生產總值、可支配收入、固定資產投資、城鎮單位就業人員、高等學校數與地級以上城市數。

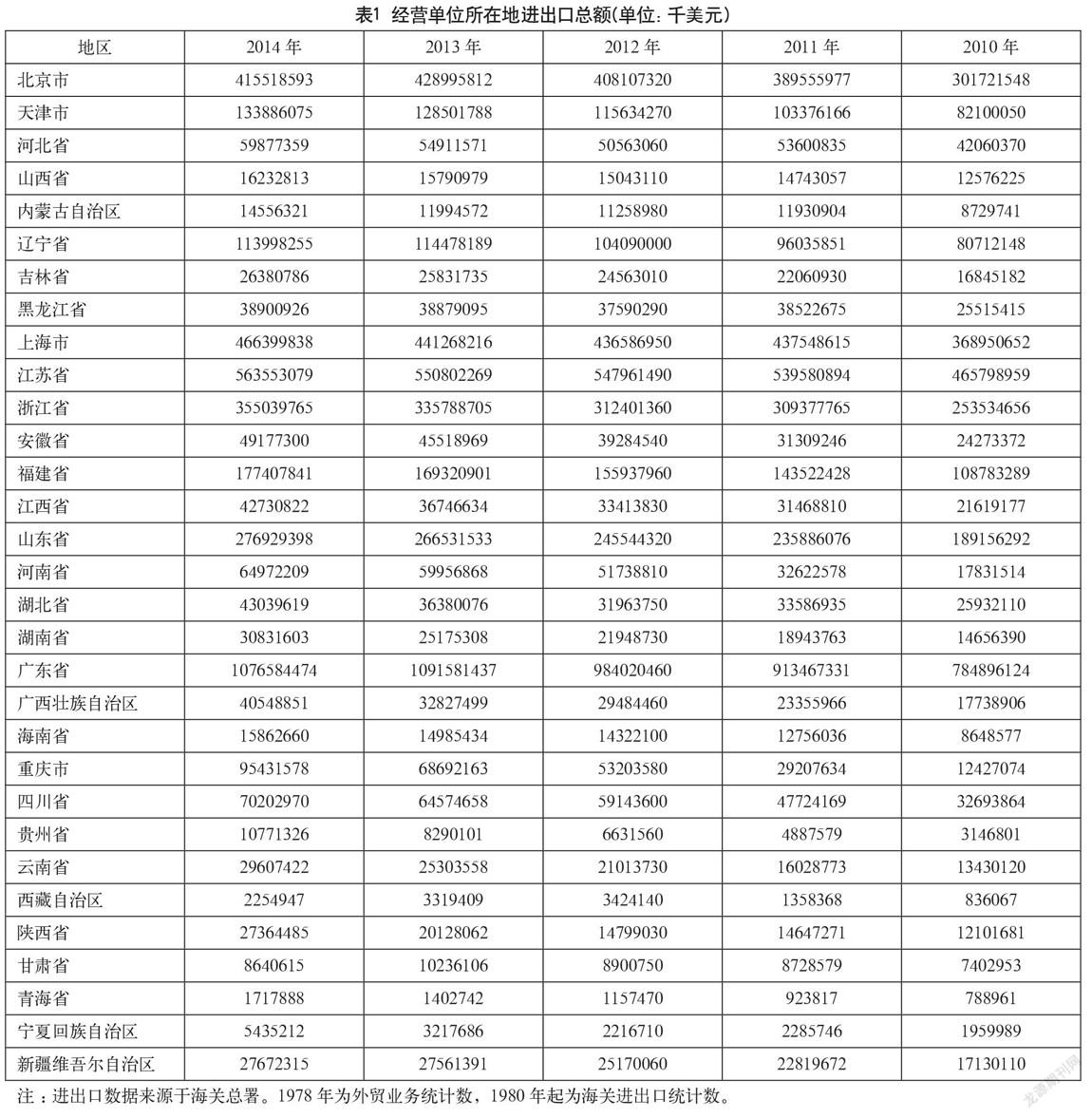
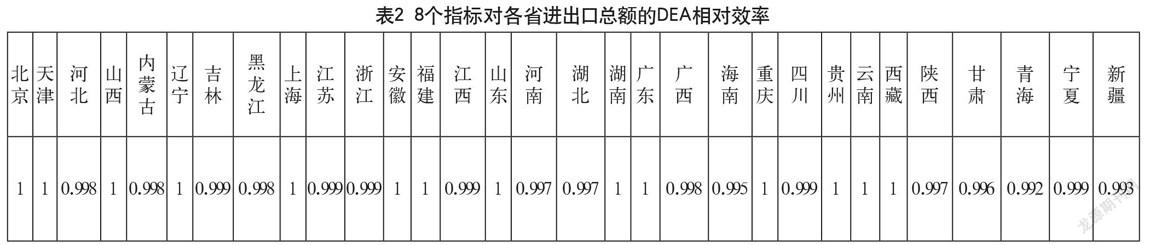
具體計算中，將確定影響各省進出口總額的8個指標作為模型（3）的輸入Xtki，將進出口總額作為模型輸出Yrkj。各省各年度進出口總額入的具體數據如表1所示。

由于本文篇幅有限，輸入8個指標的各年度數據不能一一展示。但本文的所有數據來源都來自干中華人民共和國國家統計局的官方網站的地區統計數據，可查閱到文中引用指標的具體相關數據。

3.1 算例求解與結果分析

經過MLeap對模型（3）的展開，總變量數為4960個，總約束數為1550個。由于模型展開的變量數較多，采用MLeap內部求解器求解時間成本較高，故調用Cplex12 63版本求解器求解，求解時間小于1秒得出結果。

表2是經過近似取值后的結果。對表2的結果數據分析發現，各省的DEA相對效率都為1，意味著各省從2010 2014年期間我們選中的8個指標相對進出口總額的投入/產出效率達到了近似最優的分配。但對輸入8個指標中各指標對輸出的影響還需要繼續探究。

為對輸入8個指標中各指標影響力的繼續探究，產生猜測：在各省DEA輸入數據中，其中某一項或者某幾項指標相對輸出指標的DEA效率極大（DEA效率接近于1）。在眾多指標中的顯著性很強，從而導致一次求解結果的各省DEA效率接近于1。

3.2 逐次剔除指標求解結果及分析

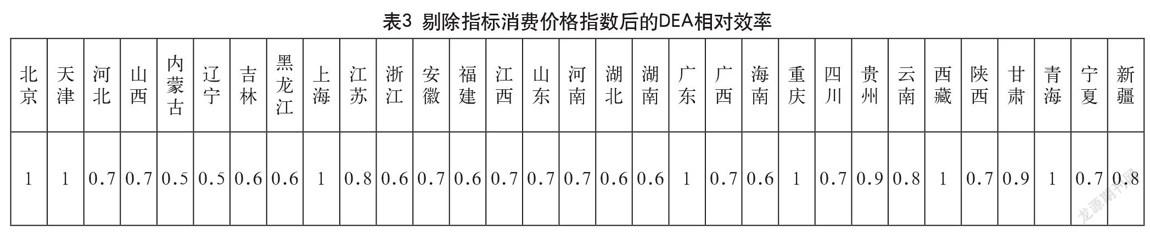
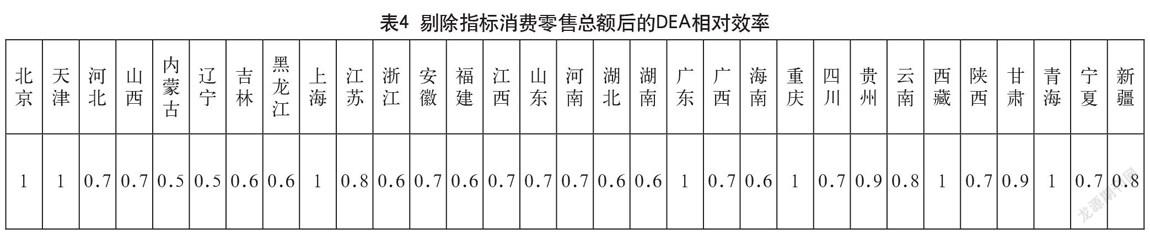
針對3 1節中的猜測，本次求解策略采用分批次求解，即每次剔除一項指標以進行檢驗。其指標的剔除順序為：消費價格指數、消費零售總額、地區生產總值、可支配收入、固定資產投資、城鎮

單位就業人員和高等學校數。再次調用Cplex12 .63對模型分批次進行求解，每次求解都能迅速得到結果（小于1秒），求解結果如表3-表9所示。

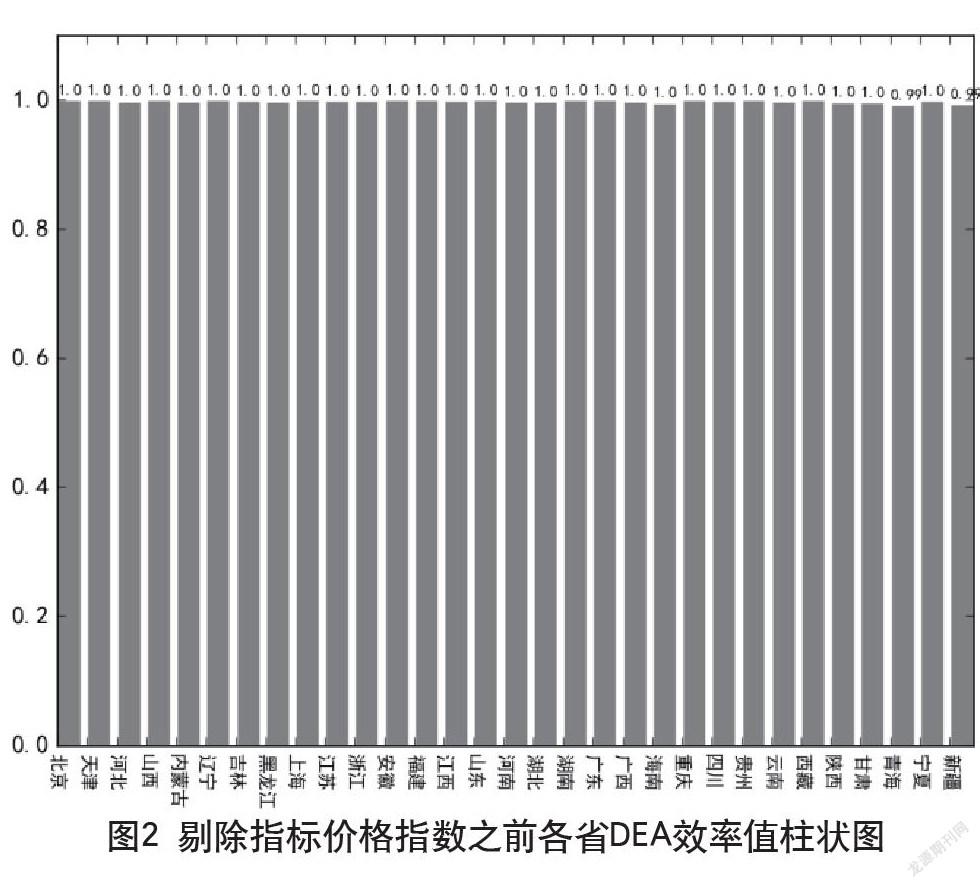
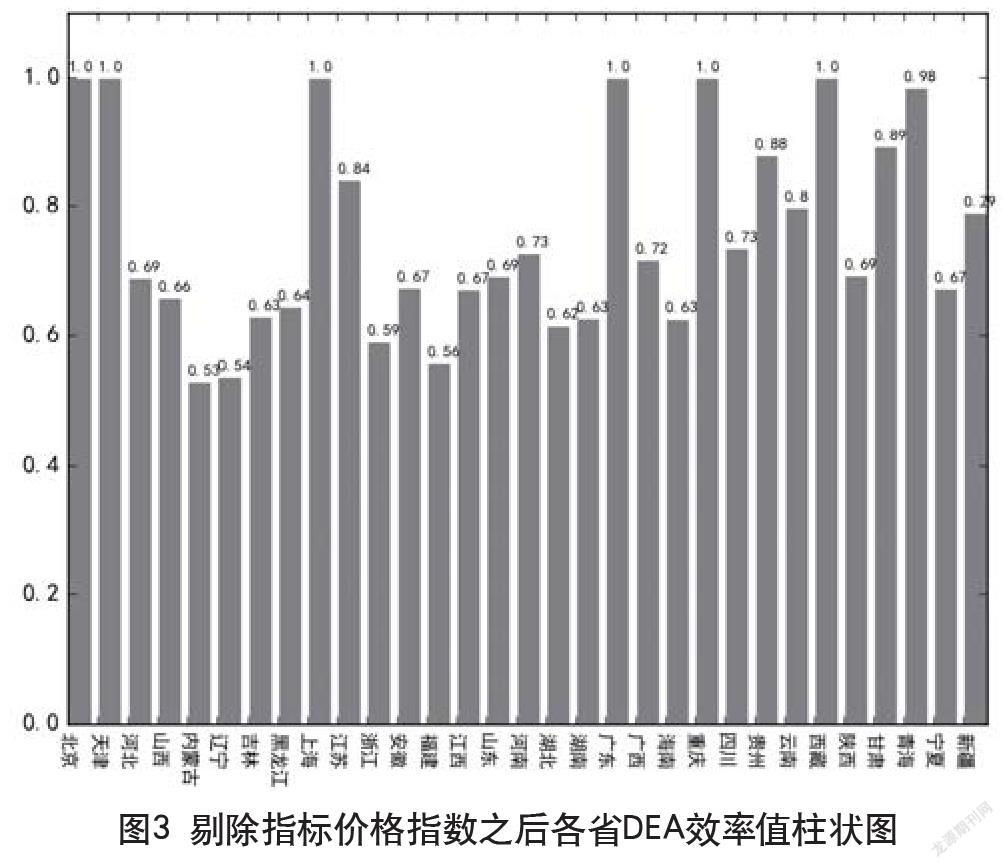
經過批次計算與對各批次結果對比分析，發現在剔除指標價格指數后各省的DEA效率值波動最大。由此可以判定在眾多的輸入指標中，消費價格指數對進出口總額的顯著性最強。而在剔除價格指數之后，顯著性較強的指標依次為：可支配收入、城鎮單位就業人員、高等學校數。具體如圖2、圖3所示。

通過以上指標顯著性的分析，基本可以得出結論：對一個地區進出口貿易總額起到顯著影響的是該地區的消費價格指數和總體居民購買力的強弱。

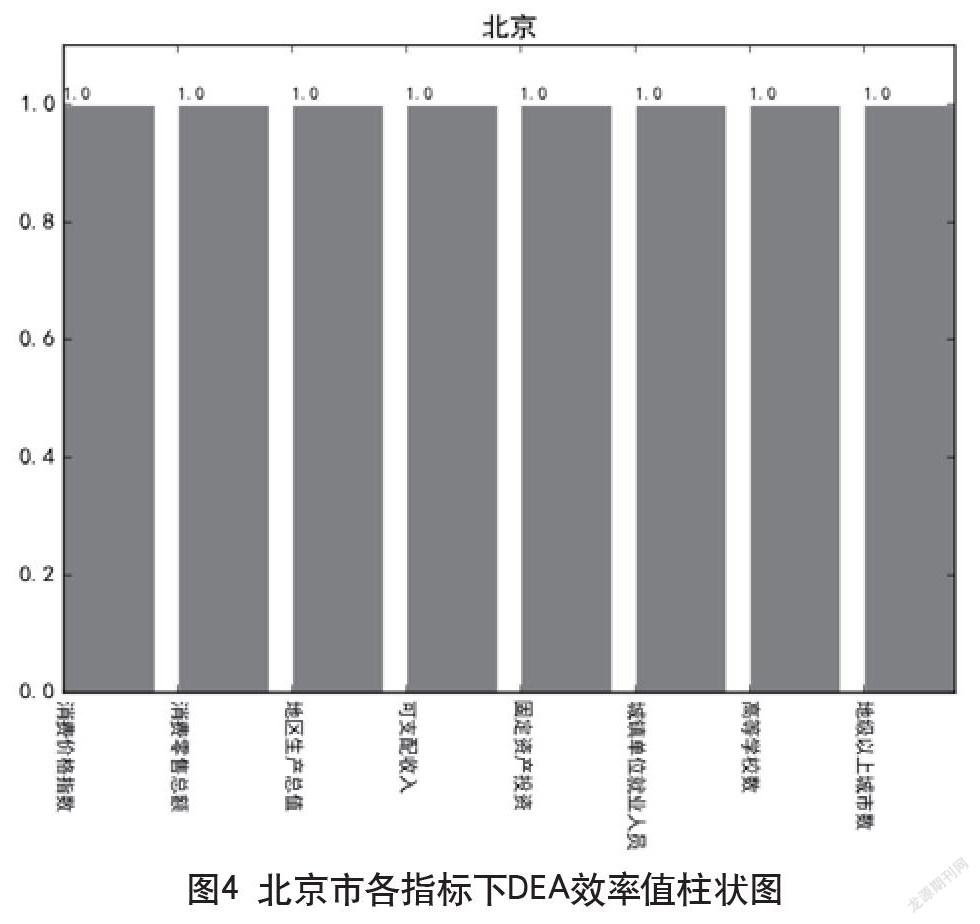
對求得結果按照城市整理分析，發現各指標下的相對DEA效率最高（剔除各指標階段下DEA效率值仍為1）的地區基本為發達城市或省份，分別為：北京、上海、天津、重慶、廣東。該結果即意味著對于上述發達城市或地區，消費價格指數、消費零售總額等輸入判別指標相對于輸出的判定指標（進出口貿易總量）來說，其輸入中的各項指標的資源分配已經達到了相對最優狀態。

由于本文篇幅有限，與上述結果相關的圖，文中未全部給出。其中北京市具體如圖4所示。

4 結語

本文給出了多時間段DEA問題的一次性求解模型，該模型可以一次建模求解出所有DMU在各個年度中的DEA效率。相對于傳統的DEA模型需要針對每個決策單元和每個年度的單獨建立模型，本文方法具有集成度更好和效率高的特點。

本文采用MLeap建模語言對數學模型給予機器表達，最后調用外部求解器對其進行求解。其中算例求解的數據來自于國家統計局的官方網站的地區統計數據。算例對消費價格指數、消費零售總額等8個指標相對于進出口總額的DEA效率值進行了計算，并采用逐次剔除指標求解的方式判定出了輸入各指標的顯著性影響。最后得出了一定有意義的結論，其在地區對外貿易量分析上有一定的指導意義。