城市空氣污染數據的真實性判別及分析

付 麗 師和欣

（綏化學院信息工程學院 黑龍江綏化 152061）

一、問題的分析

空氣中污染物濃度達到有害程度時就構成了空氣污染，污染物濃度超過了環境質量標準時，就對人和物造成了危害，它破壞了生態系統和人類正常生活的條件。[1]所有使空氣質量變壞的物質都是空氣污染物。城市空氣污染數據的采集由于各種客觀原因，會使采集的數據序列體現出一定的異常現象，因此以部分地區的空氣污染問題為背景，然后在現有的國家最新空氣污染無監測標準（HJ633-2012環境空氣質量指數（AQI）技術規定）的基礎上利用異常檢測來進行研究。通過建立數學模型，代入相關空氣質量和氣候的數據，分析空氣質量數據是否存在不真實現象，通過污染物之間的相關性來確定數據不真實及嚴重性，根據已建立的數學模型對數據進行分析，最終為環境保護和政策制定提供支撐。

二、模型建立與分析

我國現在通常采用AQI和空氣污染指數(API)來衡量空氣質量，根據國家最新空氣污染無監測標準（HJ633-2012環境空氣質量指數（AQI）技術規定）當中所規定的污染物排放限制，來建立衡量空氣質量優良等級的評價模型。

（一）單狀態量數據的時間序列自回歸模型(autoregressive，AR)。et為服從N(μe,λ2)的正態分布序列，xt為在線監測數據的時間序列，服從N(μ,σ2)，其中那么有公式：

正常狀態下每個在線監測狀態量，都不應超過相應的限值，那么假設a≤xt≤b。對所有a≤xt+k≤b，可以推導出：

由于et～N(μe,λ2)，所以根據（2）可知整個序列滿足屬于區間[a,b]，只能當α小于一個限值α0時才可實現。

因為設備產生故障的過程緩慢，此時監測到的數據通常未超出限值，很難被發現，所以在線監測數據如果沒有超出狀態量限值時，單純地用AR模型很難檢測出異常狀態。

（二）自組織神經網絡(self organized maps，SOM)對時間序列的量化。自組織神經網絡適用于數據很多、沒有標簽的狀態監測數據。SOM的輸入節點為整個序列xt，輸出節點為序列c={c1,c2,…,cn}，通過公式

對每一個xt訓練其屬于節點cj。為確保xt距其所屬節點的距離最小，用公式

反復進行循環和修正，其中學習速率γ(t)∈[0,1]，其隨著t的增大而減小。

通過SOM訓練完成后，單狀態量的時間序列xt就轉化為線性空間中的離散點時間序列ct∈{c1,c2,…,cn}：

因為ct表示關于每一個時間點t最接近于xt的節點，所以對時間序列xt的量化就用ct代表了[2]。

（三）時間序列變化過程的挖掘。SOM神經網絡的輸出節點間通過網絡拓撲結構兩兩相關。在拓撲結構中，由于SOM訓練時每個神經元節點與鄰域內的節點競爭強，與鄰域外的節點競爭弱的這一特點，在拓撲結構中通過量化后的時間序列ct將一個神經元轉移到另一個神經元，得出數據隨時間的變化規律[2]。

1.神經元所屬的概率密度函數。神經元之間的相關關系用一階轉移概率P來表示，AR(n)模型中P[ct+1|c1,c2,…,ct-n+1]為神經元之間的一階轉移概率，可得P[ct+1|ct]為AR(1)模型的一階轉移概率。c1,c2,…,cn取值分別1,2,…,n，在時刻t由式(5)可得，ct=cI的概率為

那么i(xt)的概率密度函數由式(5)和(6)得

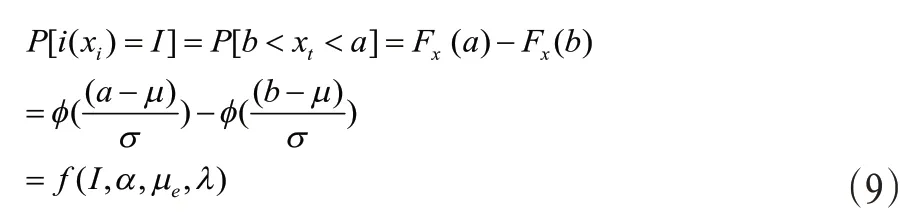
當I=1時，式(9)簡化為

當I=N時，式(9)簡化為

2.神經元之間的轉移概率。二階概率分布函數可表示為

式中cI1,cI2∈{c1,…,cN}，I1=(a1,b1)，I2=(a2,b2)。由于式(12)中xt屬于正態分布，因此xt的二階正態分布函數為

其中一階AR過程的自相關函數為ρ(k)=αk。由(6)、(9)將(13)式簡化為

對在線監測數據采用如圖1所示步驟，根據時間序列的特征量提取算法進行異常檢測。

圖1 異常檢測步驟圖

（四）多類Logistic回歸分析。我們要引入了多分類Logistic回歸模型，因為在實際問題中，響應變量有多種取值，不一定是發生及不發生兩種情況。記y是一個響應變量，取值從0到c-1，并且y=0是一個參照組，協變量x=(x1,x2,…,xp)，那么可以得條件概率：

其中k=0,1,2,…,c-1。由此可以得到相應的Logistic回歸模型：

顯然：g0(x)=0。考慮到社會因素問題，利用線性回歸分析建立空氣質量和工業生產數據之間的函數關系的數學模型，同時利用其他地區的數據，驗證了該模型有效性。線性回歸的數學模型為

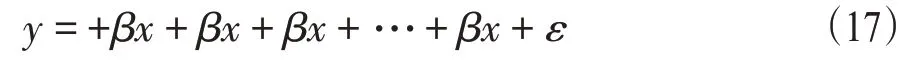
用矩陣形式表示為

其中：y=(y1,y2,…yn)T為解釋變量；α=(α1,α2,…αn)T為模型的截距項；

β=(β1,β2,…βn)T為待估計參數；x=(xij)n×k為解釋變量；ε=(ε1,ε2,…εn)T為誤差項。用α+Xβ組成的線性部分和隨機誤差項εt解釋被解釋變量的變化。線性模型估計相關的參數一般采用最小二乘估計法。估計相關的參數是回歸分析的核心也是預測的基礎。最后根據全國各省上半年PM均值排名及鋼材產量分省市統計數據，利用多類Logistic回歸分析SSPSS軟件獲得結果。

三、結語

這個模型充分地考慮到每一個因素所存在的差異，利用模型對城市的空氣質量數據進行重新鑒別，增強了數據科學性。模型對各城市空氣污染數據采用函數計算的方法來解決問題，依據已查找的數據計算分析AQI，提高了模型準確率。依據原有的數據和已計算出的數據進行對比，更加直觀的判斷了空氣污染數據的真實性。該模型在計算，制定計劃，政策分析等領域都可以廣泛應用。但是這個模型也有不令人滿意的地方，雖然要解決城市的空氣污染數據真實性問題，但是受數據的限制，只是判斷某些城市的某些天的空氣污染數據的真實性，那么位于同一空氣質量等級的城市還需要更多的數據，更多的背景加以數學處理和討論。