太陽系近地天體軌道運動的幾個問題

劉林,楊志濤

(1.中國科學院國家天文臺,北京 100101;2.南京大學天文與空間科學學院,南京 210093;3.中國科學院大學,北京 100049)

1 引言

對太陽系近地天體 (主要是近地小行星)軌道運動的了解是防御的前提,而準確的軌道確定和預報則取決于采用的動力學模型。太陽系近地天體繞日運動的力學環境,與近地衛星所處的力學環境有顯著差別,其外力源除中心天體太陽的質點引力外,主要攝動源來自各大行星的引力作用。至于表面力之類的攝動源,不外乎太陽風之類的耗散效應和源于太陽輻射的各種力學效應。對近地天體的軌道運動而言,前者無需討論,而后者歸結為輻射壓問題,但太陽實為弱輻射恒星,與之相關的動力學問題,特別是對太陽系內各大小天體 (包括彗星)運動的影響,并不重要,多年前作者就作過分析[1],本文將進一步給出該影響的定量體現,為處理近地天體軌道運動問題,提供準確的動力學模型和相應的計算方法。

2 日心系中小天體軌道運動的力學模型

2.1 小天體軌道運動的受攝運動方程

清晰的力學背景與相應的數學模型,是準確反映小天體軌道運動的重要前提。考慮到小天體的質量確實較小,可以引用限制性 (N+1)體模型,即小天體的質量可以忽略 (m=0),N體包括中心天體太陽、各大行星、冥王星和月球。

通常采用的計算單位系統中,長度單位[L],質量單位 [M]和時間單位 [T]分別為

其中,AU=1.459 978 707 00×108(km)是天文單位,S=GS/G=1.9884×1030kg是太陽質量,時間單位 [T]是導出單位。這種處理,一方面是為了各物理量的單位在一定程度上歸一化,便于對各有關物理量的量級進行估計和比較,同時也可簡化計算公式的表達。

在日心黃道坐標系中,小天體的運動方程表達如下[2,3]：

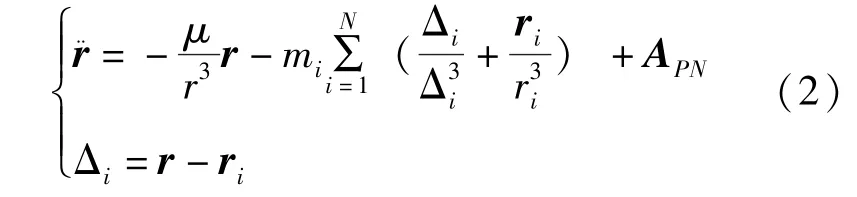
在上述歸一化的無量綱單位系統中,有μ=G(S+m)=GS=1,各大行星、冥王星和月球的無量綱質量以及日心距離分別記作和即

于是小天體軌道運動的受攝運動方程式 (2)可寫成下列形式：

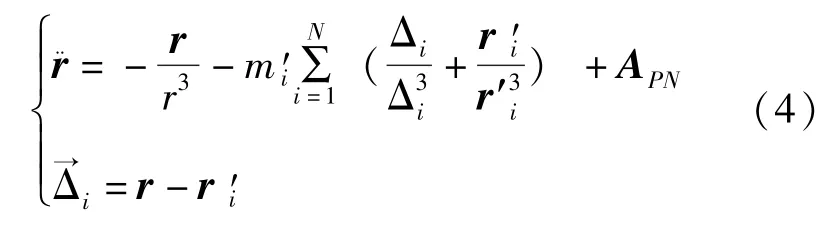
該式中的攝動項APN是源于太陽引力的后牛頓效應產生的攝動加速度,表達形式如下：

如果小天體離某大行星近到一定程度,還需要考慮相應大行星的主要非球形項 (如扁率J2)。至于與太陽輻射有關的表面力效應,對于已基本固化的小行星,其質量密度與地球接近,該影響并不重要,對于小行星監測預警和安全防御而言,不必夸大與其有關的輻射效應,后面2.4小節將會具體闡明并給出定量檢驗。

2.2 各大天體的質量與離日平均距離

這可參考下列表2列出的相關平均根數獲得。

關于月球離日的平均距離,在對近地天體受力估計中可取地球的值。

表1 質量比Tab.1 Mass ratio

表1 質量比Tab.1 Mass ratio

大行星 質量比 大行星 質量比 大行星 質量比水星 1.660136795×10-7 火星 3.227156038E×10-7 天王星 4.366244043×10-5金星 2.447838340×10-6 木星 0.954791898E×10-3 海王星 5.151383713×10-5地球 3.003489616×10-6 土星 2.858856701E×10-4 冥王星 0.732246679×10-8月球 3.694303465×10-8

表2 各大行星平均軌道的半長徑和偏心率i, i(i=1,2,…)Tab.2 Semi-major axis and eccentricity of mean orbit of planetsi, i(i=1,2,…)

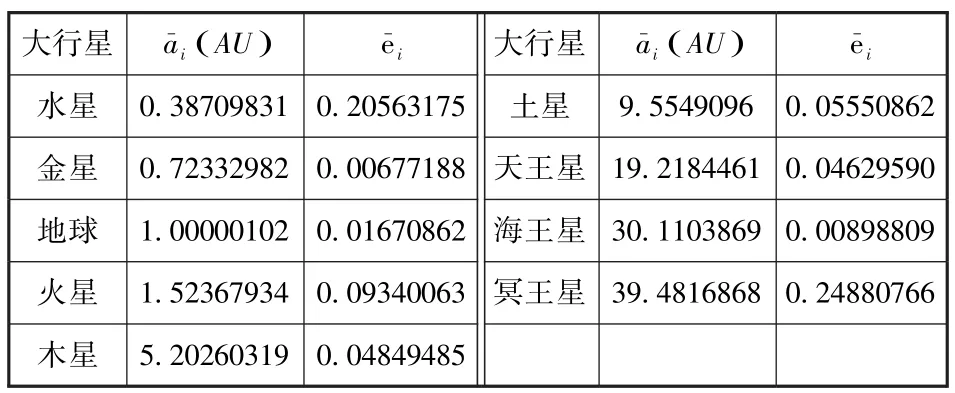
表2 各大行星平均軌道的半長徑和偏心率i, i(i=1,2,…)Tab.2 Semi-major axis and eccentricity of mean orbit of planetsi, i(i=1,2,…)

大行星 ai(AU) e-i 大行星 ai(AU) e-i水星 0.38709831 0.20563175 土星 9.5549096 0.05550862金星 0.72332982 0.00677188 天王星 19.2184461 0.04629590地球 1.00000102 0.01670862 海王星 30.1103869 0.00898809火星 1.52367934 0.09340063 冥王星 39.4816868 0.24880766木星 5.20260319 0.04849485

2.3 各大行星引力攝動加速度的量級估計

下面針對近地天體,對各大行星的引力攝動加速度進行量級估計。

(1)引力攝動加速度的近似估計

對于離太陽和運動小天體較遠的大行星 (土星、天王星等),其攝動量級的估計與地球衛星的日、月攝動類似,同樣可采用下列估計式：

否則按下式估計：

上兩式中的m′即上述各大行星相對太陽的質量比,r和r′各為小天體和攝動天體到中心天體太陽的距離,攝動天體到太陽的距離即可取上述表2中給出的平均軌道半長徑值,對軌道偏心率較大的水星和冥王星,可采用其近日距或遠日距。

對于近地天體,上述各大行星的攝動量級為ε=O( 10-9～10-4)。

(2)后牛頓效應的估計

這是引力攝動的另一類效應,近似估計如下：

在太陽系中,對于水星繞日運動而言,這一攝動量級為10-7,而對離太陽1～2個天文單位的近地天體,其攝動量級為10-8。該效應的特征是對小天體運動的軌道平面無影響,主要是對軌道近日點幅角ω有長期效應,這正是廣義相對論的幾個論據之一,水星近日點進動的檢驗,即牛頓力學無法解釋的水星近日點進動的偏差。

2.4 小天體繞日運動中承受的表面力問題

對于本文論述的問題,太陽系中各天體運動所承受的表面力主要源于太陽輻射壓,相應的量級估計式如下：

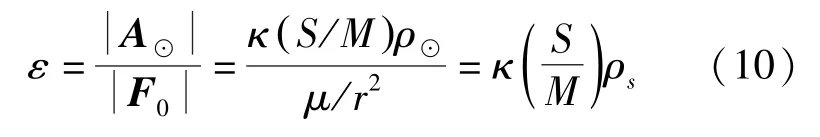
該估計式中的μ=G(S+m)=GS=1,是小天體所在位置 (日心距為r)的太陽輻射壓強度,ρs是地球附近rE=1AU處的太陽輻射壓強度,有

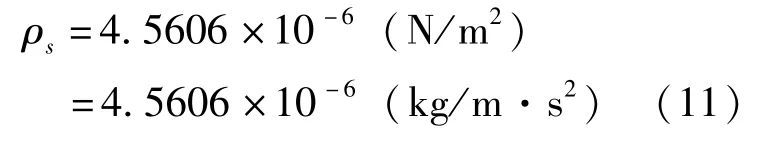
在日心系中的無量綱值 (本文采用的計算單位)為

面質比 (S/M)的常用單位是m2/kg,注意,這里的m是長度單位米的符號。在日心系統中面質比換算為無量綱值的公式為

下面舉幾個小行星的例子：

(1)小行星65803(Didymos)

Didymos是Xk型近地雙小行星,其主星的直徑約為800m,平均密度為ρ=1.7 g/cm3。作為估計,按球體形態考慮,相應的圓球截面積和球體形態的質量分別為

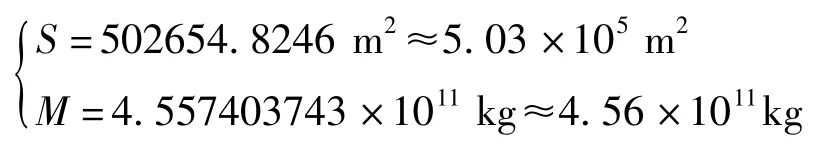
那么,面質比 (S/M)為

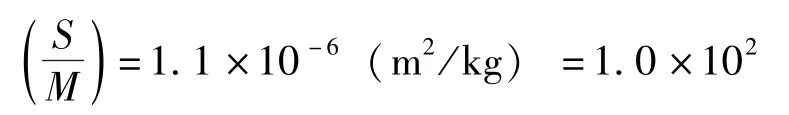
相應的太陽輻射壓攝動量級為

(2)小行星10302(1989ML)

直徑約為600m,平均密度為2.0g/cm3,質量可估為0.565×1011kg。相應的太陽輻射壓攝動量級為

(3)小行星175706(1996FG3)

直徑300m,質量2.7×1010kg,相應的太陽輻射壓攝動量級為

表3 兩顆小行星的軌道根數Tab.3 Orbit elements of two asteroids

(4)小行星99942(Apophis)

直徑1.9km,質量2.1×1012kg,密度1.4 g/cm3,相應的太陽輻射壓攝動量級為

(5)小行星433(Eros)

質量6.69×1015kg,直徑16.8km,面質比作為球形估計,相應的太陽輻射壓攝動量級為

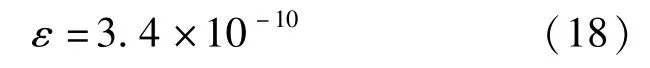
從上述幾個估計算例可以了解到,對于一般的近地小行星,作為表面力攝動源的太陽輻射壓確實不重要。至于輻射壓的大小,這從上述估計式 (10)不難看出：在質量密度相近的情況下,尺度越小的天體,承受的輻射壓越大。

2.5 小天體繞日運動中承受表面力作用大小的數值檢驗

這里考慮兩顆小行星,一顆近地小行星99942和一顆主帶小行星261936,看其在軌道演化中太陽輻射壓是否有明顯作用。兩顆星的初始歷元時刻分別對應UTC：2000年1月01日12時0分0.0秒,2016年7月31日0時0分0.0秒,相應時刻的軌道根數列于表3。

表3中半長徑a的單位是AU,其它4個角度的單位是 (°)。對上述兩條軌道作一個繞日運行周期的軌道外推,給出相應的軌道變化結果和各攝動因素影響的定量狀態。

(1)近地小行星99942

面質比(S/m)=10-6(m2/kg),運行一個周期 (395.238592天),結果列于表4和表5。

(2)主帶小行星261936

面質比(S/m)=10-6(m2/kg),運行一個周期 (1487.960956天),結果列于表6和表7。

上列各表中的力模型序號 (1)-(10),依次為

表4 瞬時根數狀態Tab.4 Instantaneous elements states

表5 空間位置、速度狀態Tab.5 Space position and speed states

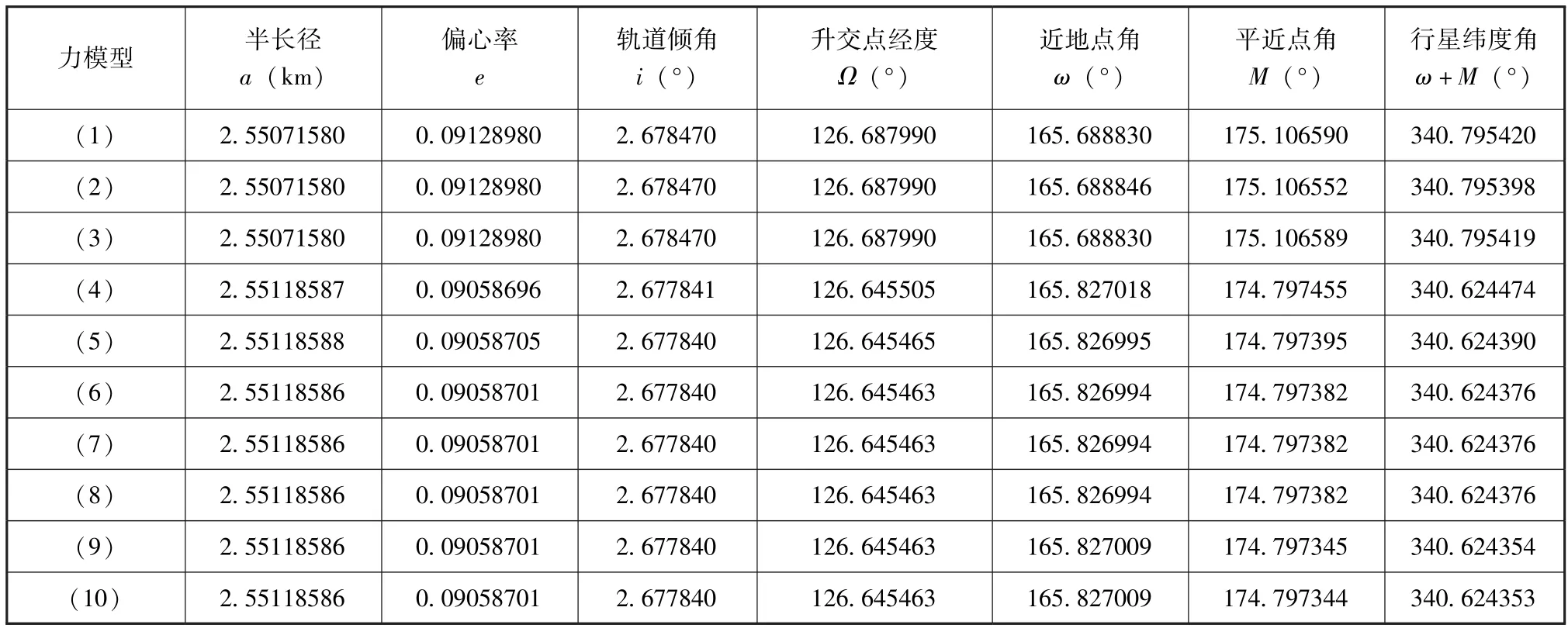
表6 瞬時根數狀態Tab.6 Instantaneous elements states

表7 空間位置、速度狀態Tab.7 Space position and speed states

序號中的1或0,分別表示考慮或不考慮對應的攝動源,相應的12個攝動源,依次對應8個大行星 (水星,金星,…,海王星)、冥王星、月球、后牛頓效應和太陽輻射壓。

從上述結果不難看出：前面對各攝動影響的定量分析是準確的,對于基本固化的小天體,面質比較小,就軌道運動而言,表面力之類的外力攝動影響確實無需考慮,特別在空間防御領域,不應受其“干擾”。作者曾采用上述力模型對應的受攝運動方程 (2),處理過“近地小行星與地球交會問題”的研究[4],所獲結果與國際小行星中心 (MPC)公布的結果相符。

3 小天體軌道運動解擬采用的數學方法[5,6]

與人造地球衛星的運動狀態不同,對于近地天體的軌道運動,若要構造攝動分析解 (即小參數冪級數解),將會涉及第三體攝動函數展開中出現的外攝 (r/r′＜1)和內攝 (r/r′＞1)情況,特別是兩種狀態出現在同一攝動天體的狀態,這給攝動分析解的具體構造帶來困難。

鑒于近地天體的運動不同于人造地球衛星,幾乎一年左右才繞日運行一圈,軌道預報的緊迫性不同于近地空間目標監測防御的要求,擬直接采用數值方法實現軌道預報計算。對于近地天體軌道運動方程的數值解,其狀態量的選擇可考慮采用相應的軌道根數σ,其運動方程表達如下：

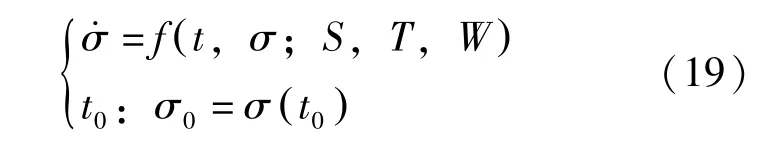
考慮到算法的普適性,擬采用同時消除小偏心率和小傾角的無奇點根數σ(即適用于0≤e＜1.0,0°≤i＜180°.0) 作為上述運動方程 (19)的積分狀態量。所有攝動源對應的攝動加速度分量S,T,W可由Fε形成,即

采用上述處理方法,導致整個計算過程與直接采用坐標、速度(r,)的流程沒有明顯差別,但卻避開了原運動方程 (2)或 (4)右端無攝項的計算,該項既是數值積分過程中制約積分步長增大的關鍵項,又是積分截斷誤差傳播最嚴重的誤差源。有關具體細節不再介紹,僅供參考。