福建省高等教育對經濟增長的貢獻實證分析

潘邦貴

福建省作為率先發展起來的東部沿海區域，也是“一帶一路”倡議的重要實踐省份，其教育在經濟發展的過程中得以良好發展，而且發揮著日益重要的作用。尤其是近年來高等教育獲得了長足的發展。1952年至2017年，全省高等教育的在校生人數從0.47萬人增加到75.1萬人，專任教師人數從611人增加到45398人(詳見圖1)。2018年，全省高等教育學校89所，研究生教育招生1.88萬人，在校生5.31萬人，畢業生1.22萬人。普通高等教育招生23.86萬人，在校生77.24萬人，畢業生20.43萬人。普通高校畢業生就業率為97%。[1]舒爾茨認為，人力資本對經濟增長具有重要作用。那么，快速發展的高等教育對福建省的經濟增長究竟有多大貢獻？本研究利用人口普查數據和某些年份1%人口抽樣數據，結合柯布-道格拉斯生產函數，對福建省高等教育對經濟增長率的貢獻率進行了計算分析，并結合研究結果，針對如何提高全省高等教育對經濟增長率的貢獻率建言獻策。

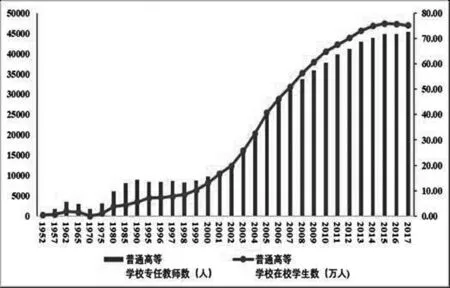
圖1 1952—2017年福建省普通高校專任教師數和在校學生數

數據來源：2018年《福建省統計年鑒》

一、福建省高等教育對經濟增長貢獻率的模型選擇

高等教育對經濟增長貢獻率的分析，國內外學者方法各異。但是，多數都是基于柯布-道格拉斯生產函數來進行實證分析的，就全國范圍而言，宋華明、王榮(2005)用C-D函數測算了1990—1999年間我國高等教育對經濟增長率的貢獻，結論為高等教育對經濟增長率的貢獻很低。因此，要加快經濟增長速度，實現社會全面小康，就必須大力發展高等教育，推進高等教育大眾化。朱迎春、王大鵬(2010)[2]在EFDenison和A Maddison算法基礎上進行延伸，結合C-D函數，運用省際面板數據測算高等教育對區域經濟增長的貢獻，并比較區域間差異。研究結果表明，1996—2006年中國高等教育對經濟增長的貢獻率平均僅有1.267%，且地區間差異較大，呈現由東向中西部地區逐步遞減的梯次分布。胡德鑫(2017)[3]以丹尼森因素分析法作為理論基礎，在柯布-道格拉斯生產函數的基礎上，對我國高等教育對經濟增長的貢獻進行測算。結果表明，1996—2014年我國勞動投入彈性系數為0.44，高等教育對經濟增長的直接貢獻率為1.82%；直接貢獻額由1996年的60.49億元增長到2014年的271.28億元，年均增長率為8.69%；與發達國家相比，我國高等教育對經濟增長的貢獻偏低。燕玉鐸等(2011)[4]用同樣的方法，全面測算1991—2008 年我國高等教育對經濟增長的貢獻。結果表明，1991—2008 年我國高等教育對經濟增長的貢獻呈上升趨勢，增長速度較快。高等教育對經濟增長的貢獻率為 0.81%，與發達國家相比，仍存在較大差距。從分專業角度看，邸俊鵬、孫百才(2014)[5]通過將高等教育劃歸為不同的專業類別，考察1978—2010年其對國民經濟各部門的影響，實證研究結果表明，高等教育對我國經濟產出產生了積極的作用，高等教育對工業部門的影響最大，對農業部門的影響在統計上不顯著。工業部門中理工類和農林類專業的影響較大，高等教育對服務業部門產出有顯著正效應。同時，需要意識到，一定的經濟發展水平決定著高等教育的專業配置和培養規模，而合理的高等教育專業設置和適當的規模反過來又會助推經濟的快速發展。因此，需重視高等教育和經濟增長的協調發展，從而更好地發揮高等教育服務社會的功能。聶娟、辛士波(2018)[6]采用 2017 年中國大學排名數據，分析各省高等教育質量的差異性，以高等教育質量與經濟發展關系為基礎，探索分析高等教育質量地域差異的成因。根據 C-D 生產函數模型，測算31個地區高等教育對于經濟增長的貢獻率，探討區域高等質量水平對經濟增長的效應差異性。研究發現，從國內高等教育發展現狀來看，整體教育質量在不斷提升，但仍存在區域性差異問題；基于高等教育質量評價角度，師資隊伍結構、學生發展能力、院校科研水平均是影響高等教育發展的重要方面；各省份經濟發展不平衡與教育質量密切相關，這是引起高等教育質量的經濟增長效應的主要原因。總體而言，多數研究認為，從全國范圍來看，高等教育對經濟增長的貢獻相對較低，遠低于國際水平。

就地區而言，多數研究認為高等教育對地方經濟的貢獻相對全國平均水平是比較高的。以山西省為例，郎永杰等(2011)[7]根據Cobb-Douglas Production Function模型，測算出2000年至2009 年山西教育對經濟增長的貢獻率為5.82%，其中高等教育對經濟增長的貢獻占 4.7 個百分點。可以看出，山西省高等教育對經濟增長的貢獻率高于全國歷史平均水平，與其他有關山西省以往不同時間段高等教育對經濟增長貢獻率的測算結果進行比較，山西省高等教育對經濟的貢獻率是不斷提高的，增長趨勢明顯。以安徽省為例，張根文、黃志斌(2010)[8]采用柯布-道格拉斯生產函數構造的模型,基于2000年至2007年的相關數據, 測算了安徽省高等教育對經濟增長的貢獻率。結果表明,安徽省高等教育對經濟增長的貢獻率仍然較低。以福建省為例，游璇(2015)[9]利用1984年至2012年的年度統計數據對經濟增長和高等教育發展的關系進行實證檢驗，采用協整模型，得出福建省高等教育發展與經濟增長間存在長期均衡關系的結論。以四川省為例，楊建國等(2012)[10]運用柯布-道格拉斯生產函數并通過實證研究方法推算出了高等教育對四川經濟增長的貢獻率為8.92%，這一比例在西部地區是比較突出的，發展教育與發展經濟具有內涵關聯關系。以長三角地區為例，王黎愷(2014)[11]采用數據回歸分析的方法，研究發現高等教育對長三角經濟增長的正向影響。以黑龍江省為例，崔玉平、王小婷(2017)[12]基于二級嵌套 CES 生產函數模型，估算2000—2013年高等教育投資存量增長對地區經濟增長量的年平均貢獻率為4.38%。以吉林省為例，林鳳麗等(2015)[13]測算了吉林省2000年至2012年間高等教育對經濟增長的貢獻率，并把計算結果同全國平均水平、東北三省數據進行了對比分析，發現吉林省高等教育對經濟增長的貢獻率低于全國平均水平，且在東北三省中排名遼寧省之后。以江蘇省為例，姚文韻、陳飛宇(2012)[14]分析發現教育發展與經濟增長相關性顯著，教育經費投入與經濟增長、教育規模增長、事業發展需求之間存在不均衡的現狀。以民族自治區為例，王邦權(2018)[15]借助柯布-道格拉斯生產函數和全國及地區統計數據，結果發現高等教育對經濟增長拉動作用差異顯著，民族自治區高等教育對經濟增長率的貢獻與全國平均水平相比還有較大差距。

整體來看，大多數研究采用的實證分析方法都是C-D函數，除了上述研究之外，還有琚曉星等(2007)[16]、張開洪(2008)[17]、游銳(2012)[18]、李洪天(2001)[19]和劉林(2001)[20]等。但是，現有的研究忽視了作為東南沿海發展快速的福建省的高等教育的發展對經濟增長的貢獻，且使用的實證分析方法缺陷明顯。鑒于此，本研究借鑒經典的柯布-道格拉斯生產函數，結合本研究的實際情況，對福建省高等教育對經濟增長的貢獻率進行分析。

首先，由于柯布-道格拉斯生產函數(簡稱C-D生產函數)的基本形式：

Q=ALαKβ

(公式1)

而教育因素蘊含在勞動L中，故此本研究中需要對C-D生產函數進行變形：

Q=AKα(L0tEt)β

(公式2)

其中，Q為產出量；A為技術常數；K代表資本；α代表資本的產出彈性；Lot表示不包含教育因素在內的初始勞動力，Et表示教育投入量，兩者的乘積就是勞動量L；β代表勞動的產出彈性。

其次，對公式2求對數，可得：

q=lnA+αlnK+βlnL0+βlnE=a+αk+β(l0+e)

(公式3)

在上式中，q為一段時間內的GDP年均增長率，a為年均技術進步率，k為年均資本增長率，l0為初始勞動年均增長率，e為教育投入量的年均增長率。

最后，根據上式可知，教育對經濟增長率的貢獻率(用Ce表示)為：

Ce=βe/q

(公式4)

由于國際上通常用教育綜合指數的年均增長率(簡寫為Re)來表示教育投入量的年均增長率，因此，公式4可變化為：

Ce=βRe/q

(公式5)

所以，教育對經濟增長率的貢獻率的計算公式即為Ce=βRe/q。

二、福建省高等教育對其經濟增長貢獻率的分析

(一)指標選取和數據來源

根據本研究的模型選擇，考慮數據的可得性，選取1990年至2014年間福建省各種受教育程度人口所占比重為研究指標，其中，數據主要來源于1990年、2000年和2010年福建省人口普查數據，1995年、2005年、2013年和2014年的《福建省1%人口抽樣調查報告》《中國勞動統計年鑒》《中國人口和就業統計年鑒》等。

表1 從業人員受教育程度構成(%)

(二)高等教育對其經濟增長貢獻率的計算過程

第一步：計算出各年份從業人員人均各級受教育年限。為了方便計算，我們用X1代表從業人員中受過小學教育的人口占總人口的比重，X2代表受過初中教育的人口占總人口的比重，X3代表受過高中教育的人口占總人口的比重，X4代表受過高等教育(即大專及以上)的人口占總人口的比重。同時，假設小學的受教育年限平均為6年，初中和高中的受教育年限平均各為3年，高等教育的受教育年限平均為4年。則：

從業人員人均受小學教育年數=(X1+X2+X3+X4)*6/100

從業人員人均受初中教育年數=(X2+X3+X4)*3/100

從業人員人均受高中教育年數=(X3+X4)*3/100

從業人員人均受高等教育年數=X4*4/100

按照上述算法，計算結果如表2所示。

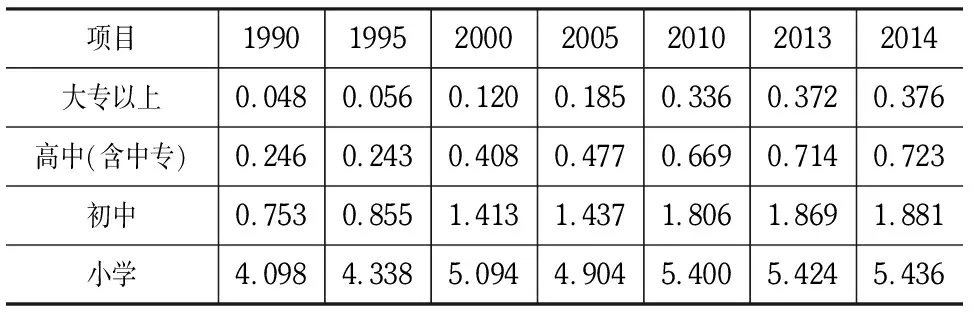
表2 歷年人均受教育年限(年)

第二步：計算出相應年份的教育綜合指數。關于不同受教育程度從業者的勞動生產率的確定，張開洪(2008)認為如果中部六省小學文化程度的勞動者的勞動生產率定為1，則初中、高中和高等教育勞動者的生產率分別為：1.2、1.4和2.0。琚曉星等(2007)根據重慶市的數據計算出初等教育、中等教育和高等教育的勞動生產率分別為1.0、1.4和2.0。游銳(2012)則假定福建省初等教育、中等教育和高等教育從業者的勞動生產率分別為1.0、1.5和2.3。綜合而言，他們對不同受教育年限的勞動者的生產率的分析結果并無太大差異。在本研究中，我們采用較為綜合的結果，借鑒張開洪(2008)的做法，假設小學、初中、高中和高等教育從業者的勞動生產率分別為1.0、1.2、1.4和2.0，則教育綜合指數(E)=小學人均受教育年限+1.2*初中人均受教育年限+1.4*高中人均受教育年限+2.0*高等教育人均受教育年限。計算結果見表3。

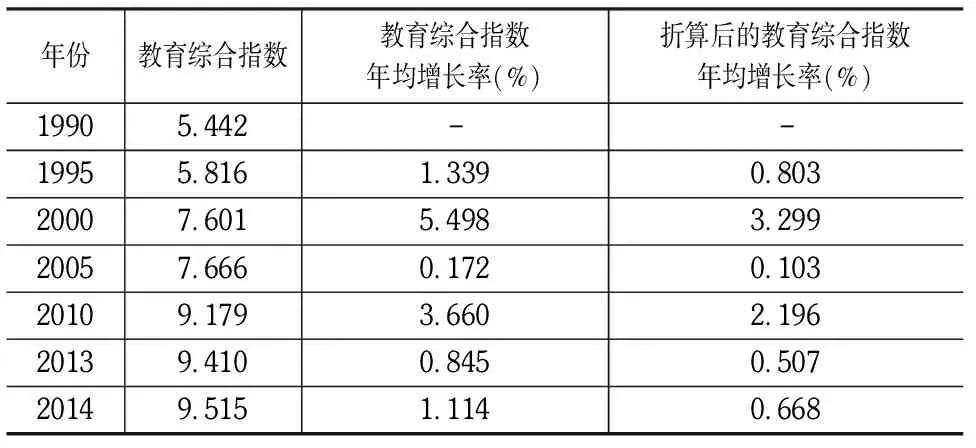
表3 教育綜合指數和折算前后的教育綜合指數年均增長率

第三步：計算教育綜合指數年均增長率Re。如果用Et表示報告期的教育綜合指數，E0表示基期的教育綜合指數，且n表示報告期年份t和基期年份0之間的時間間隔，則Re=(Et/E0)1/n-1。計算結果見表3。

第四步：計算折算后的教育綜合指數年均增長率β*Re。由于國內外學者多數認為勞動生產率的差別不一定全是由于教育程度不同造成的，也受其他學者的影響，所以有必要對Re進行折算。關于折算系數β的數值大小，琚曉星等(2007)和游銳(2012)按照西方通行做法0.6計算，張開洪(2008)則按照丹尼森系數0.73計算。在此，我們采用西方的通行做法，將折算系數β的數值定為0.6。計算結果見表3。

第五步：計算排除高等教育后的教育綜合指數年均增長率。方法類似于前述四步。即：排除高等教育后的教育綜合指數=小學人均受教育年限+1.2*初中人均受教育年限+1.4*高中人均受教育年限。而且，排除高等教育后的教育綜合指數年均增長率的計算方法同第三步。計算結果見表4。

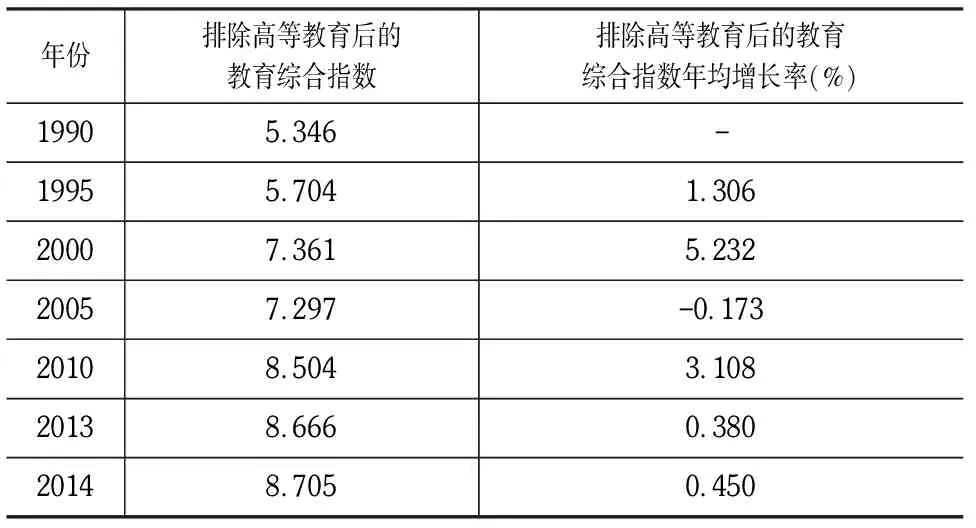
表4 排除高等教育后的教育綜合指數及其年均增長率

第六步：計算高等教育在教育綜合指數年均增長率中所占的比重。由第三步和第五步的計算結果可得，高等教育在教育綜合指數年均增長率中所占的比重(Ep)=教育綜合指數年均增長率-排除高等教育后的教育綜合指數年均增長率。計算結果見表5。

表5 歷年高等教育在教育綜合指數年均增長率中所占比例(%)

第七步：計算各時間段內的GDP年均增長率(q)。q=(GDPt/GDP0)1/n-1，n表示報告期年份t和基期年份0之間的時間間隔。結果見表6所示。

表6 歷年GDP年均增長率(%)

第八步：計算高等教育對GDP年均增長的貢獻率(Cr)。在此，需要先計算出教育對GDP年均增長的貢獻率(Ce)：Ce=β*Re/q，然后借助Ce計算Cr。Cr=Ce*Ep。結果見表7所示。

表7 高等教育對GDP年均增長的貢獻率(%)

由表7可知，1995年至2000年期間，高等教育對經濟增長的貢獻率增長迅速，在平均速度為10.26%的GDP增速中，全省高等教育對其貢獻率達到0.086%。同時，2005年至2010年期間，在平均速度為14.46%的GDP增速中，全省高等教育對其貢獻率達到0.084%。究其原因，主要是受益于1999年全國大學擴招以后的高等教育畢業生人數增加，對經濟增長的貢獻自然就較為顯著。但是，2000年至2005年期間，由于受東南亞金融危機和全國“非典”等情況的影響，福建省作為沿海開放城市，其發展勢必受到株連，而經濟對高等教育亦有反作用，故其高等教育對全省經濟增長的貢獻下降也較為迅速。同時，2010年以后，受經濟的快速發展、經濟轉型升級和高校畢業生供需日益增加，甚至供過于求等影響，高等教育對經濟增長的貢獻雖不如2005年至2010年那么高，但是其貢獻率也相對較好。不過，就整體而言，貢獻率偏低。

三、結論與建議

本研究結合C-D函數對福建省高等教育對經濟增長的貢獻進行研究，發現全省高等教育對經濟增長的貢獻不同年份波動較大，但是整體依舊相對偏低。為此，可從以下幾個方面提升高等教育對全省經濟增長的貢獻率。

第一，做有特色的高等教育，明確人才培養目標，根據專業特色、學校特色和地區經濟特色創新培養模式，有針對性地進行相應學科的專業布局，以便更有針對性地為全省的經濟發展作出貢獻。

第二，完善政策法規，引入民間資本積極參與高等教育發展，增強市場活力。政府要通過一定的措施鼓勵對高等教育的資本投入，[21]發揮民間資本的巨大能量，促進高等教育學校開放辦學，增強其資金實力，更好地為教學和科研活動服務。同時，也能強化產學研相結合的發展過程，增加科研成果的市場轉化率，進一步為高校、企業和市場謀得利益。

第三，強化與其他院校的交流合作，進一步提升高等教育學校的辦學質量。福建地理位置優越，也是重要的出海口，四通八達。因此，可利用地理優勢，加強與臺灣地區高校的交流與合作，側重發展雙邊交流項目。此外，擴大留學生教育與合作辦學，通過多種途徑吸收國外高校的優秀辦學經驗，從根本上提升全省高校的辦學質量。

第四，促進高校研究成果的轉化，使科學研究與市場經濟緊密結合，建設技術轉移中心和技術產業化基地，加快高校科技成果向現實生產力的轉化。