三維線性相位FIR數字濾波器對稱特性的設計

文/殷仕淑 武岳 常郝

1 引言

對多維信號處理的研究工作最早可以追溯到上世紀60年代。D.P. Petersen 與D. Middleton在文獻[1]中首次開展了對多維頻帶有限信號進行抽樣和重建工作的理論研究。此后，在多維數字濾波器的研究領域里，致力于二維數字濾波器理論及設計方法的研究工作占據絕大部分分量，發展很快。相較而言，由于數據量大，系統復雜度增加，處理三維空間信號（例如三維醫學影像信號，地球物理空間信號等）的三維數字濾波器（Three dimensional digital filters: 3D DF）的相關理論及設計工作進展不大。設計一個長度為10的FIR一維數字濾波器，最多有10個未知變量待求。設計一個三維長度都為10的FIR三維數字濾波器，待求的未知變量數為1000。雖然濾波器的設計問題描述相同，但龐大的未知變量數對于算法的有效收斂是個極大考驗。雖然可以利用低維濾波器去處理三維信號，但考慮到數據之間的相關性，尤其是在移動圖像處理、機器視覺、醫學圖像處理、地震信號處理和其他地球物理等三維空間信號處理領域中，發展三維數字濾波器的概念和研究三維數字濾波器的設計問題仍舊是不可避免的。

本文主要討論線性相位三維FIR數字濾波器的分類和設計工作。與IIR濾波器相比，FIR系統的單位脈沖長度有限，滿足絕對可和系統穩定性判斷條件。其次，FIR數字濾波器可以實現線性相位響應。最初FIR三維數字濾波器的設計是以一維數字濾波器為原型，采用McClellan變換(McClellan transform)進行轉換得到的[2-7]。遺憾的是，這種方法無法精確控制三維數字濾波器的頻率特性。優化迭代算法是另一種比較常見的用來設計FIR 三維數字濾波器方法。濾波器的設計問題寫成線性規劃問題求解，且不用約束其系統穩定性[8,9]。在文獻[10,11]中，解析最小二乘法用來求解FIR三維數字濾波器。為了降低設計工作的計算復雜度，FIR三維數字濾波器的設計工作充分利用三維空間的對稱特性[4,5,8-13]。即便如此，在上述文獻中所獲得的FIR三維數字濾波器頻譜特性仍舊不太令人滿意。此外還有一些工作嘗試采用比較新穎的算法思想來解決FIR多維數字濾波器的設計問題，如模擬退火算法[14]，凸集投影法[15]，但遺憾的是三維數字濾波器的實驗數據并沒有被成功獲取。

研究三維數字濾波器的對稱特性可以從頻域（幅度響應，相位響應）和空域（或稱時域，即系統單位脈沖響應或濾波器系數）兩個方面入手，如：球面對稱和立方對稱等屬于頻域概念[16-18]。基于平面對稱概念所定義的多種不同幅度響應對稱特性以列表的形式報告于[19]。在文獻[8]中，作者對濾波器的幅度平方響應對稱性進行研究，得出三維數字濾波器的幅度平方響應共有47種不同類型對稱性。而在文獻[11]中，基于單位脈沖響應三維數據的長度奇偶性和對稱奇偶性的不同組合，得出共有64種不同類型的線性相位FIR三維數字濾波器類型。類似地，在1998年，線性相位一維數字濾波器單位脈沖響應對稱性的四種組合被移植至多維系統[20]。本文中，在文獻[11,20]工作的基礎上，擬對單位脈沖響應三維數據對稱性的64種組合進行分析，剔除冗余數，初步提出20種不同類型的線性相位FIR三維數字濾波器。結合零點位置分析，給出設計不同種類（低通、高通、帶通和帶阻）線性相位FIR三維數字濾波器的單位脈沖響應對稱特性的選取。為了得到線性相位三維FIR數字濾波器，本文把此類型濾波器的設計問題寫出凸問題，采用約束凸規劃進行求解[21]，獲得具有良好頻率特性的線性相位三維FIR數字濾波器。最后給出設計實例。

2 3D FIR線性相位數字濾波器

對于一個因果的FIR三維數字濾波器，其單位脈沖響應可以用三維矩陣數據來表示：其系統函數表示為：

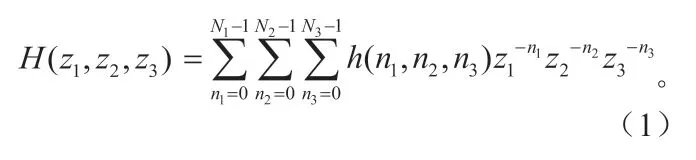
系統的頻率響應定義為濾波器單位脈沖響應的離散時間傅里葉變換（Discrete-time Fourier transform: DTFT），是式（1）中z變量在z平面單位圓上取值，即，

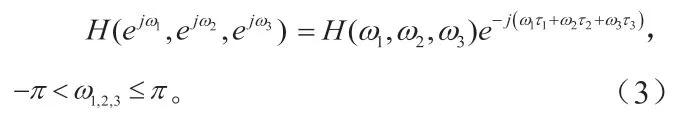
類似于一維數字濾波器單位脈沖響應的對稱性分析， FIR三維數字濾波器在三維方向濾波器長度在每一維度方向上可能是奇數長度也可能是偶數長度，且在每一維度方向可能是奇對稱，也可能是偶對稱的。因此，FIR三維數字濾波器的單位脈沖響應每一維度方向有四種可能組合：

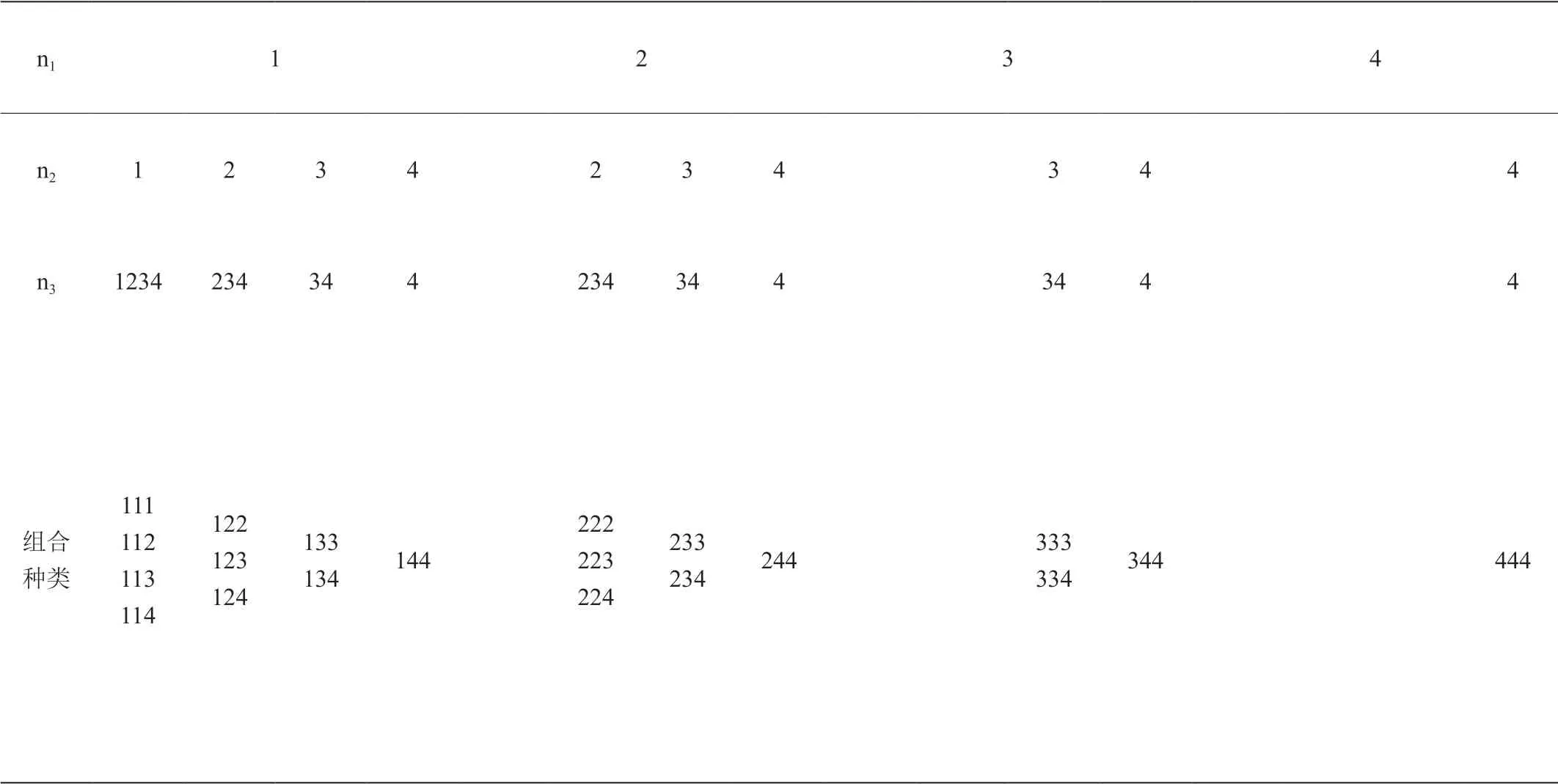
表1：單位脈沖響應三維方向對稱特性組合種類

（1）長度為奇數且偶對稱；

（2）長度為偶數且偶對稱；

（3）長度為奇數且奇對稱；

（4）長度為偶數且奇對稱。

也就是文獻[11]中所說的一共有64種組合。我們可以用數組（111），（112），（121），。。。，（444）來表示這64種組合。

利用線性相位濾波器單位脈沖響應的數據對稱性，我們可以很方便地寫出表1中三維FIR線性相位濾波器的頻率響應。例如，現有某FIR三維數字濾波器的單位脈沖響應三維方向對稱特性為表1中組合“111”，則有：

其中，

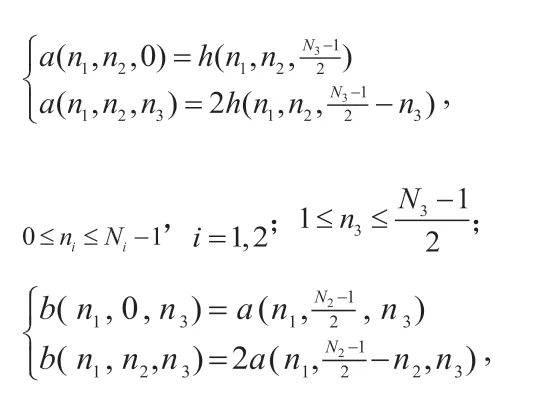
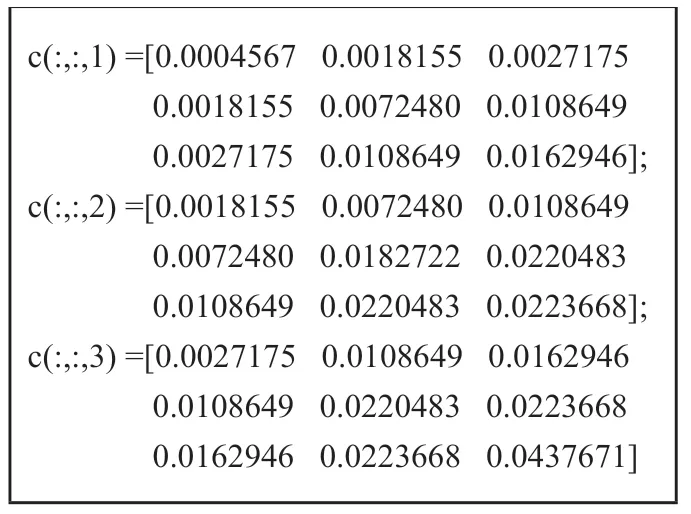
表2：例1中三維線性相位FIR濾波器系數

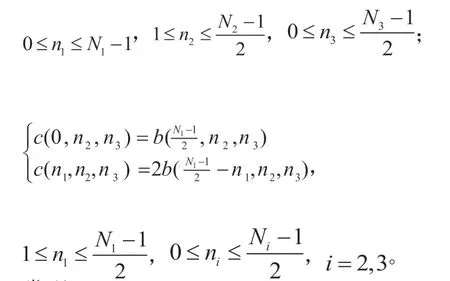
發現：

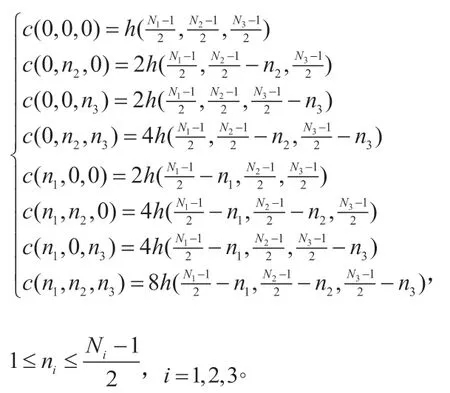
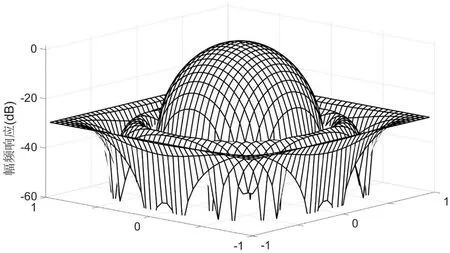
圖1：三維FIR數字濾波器幅頻特性

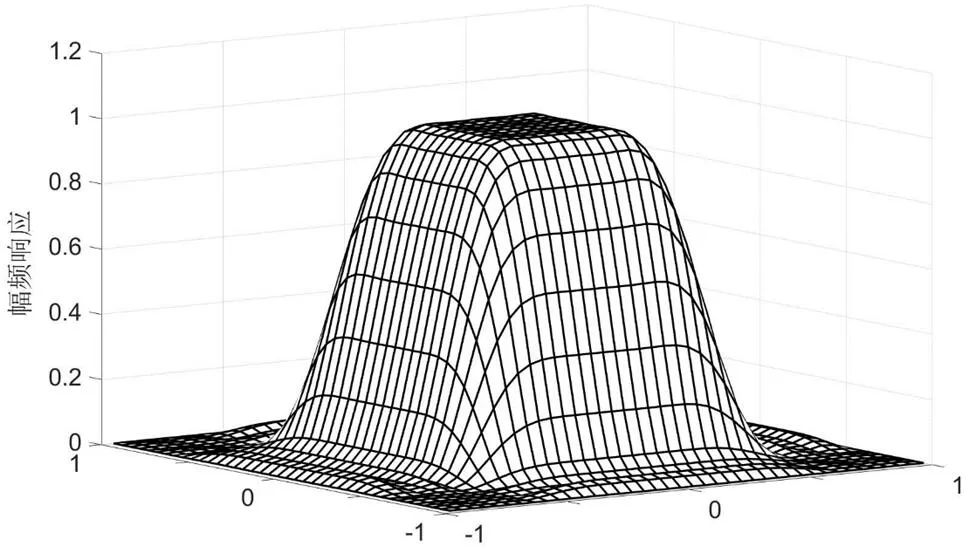
圖2

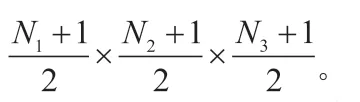
再例如：對于組合（444），利用濾波器系數對稱特性，濾波器的頻率響應可以寫成：

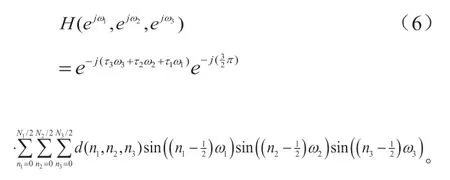
其中，

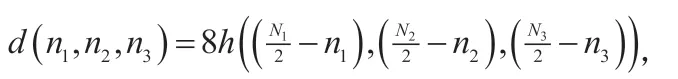
對于一維線性相位FIR濾波器的四種類型，類型1可用于設計低通（LP），帶通（BP），高通（HP），和帶阻（BS）濾波器；類型2可用于設計LP和BP濾波器；類型3僅能用于設計BP濾波器；類型4可用于設計HP和BP濾波器。因此，表1中20種類型中適用于設計在三個維度里具有相同通阻特性的線性相位FIR濾波器為：低通（111，112，122，222）、帶通（全部組合）、高通（111，114，144，444）和帶阻（111）。如果濾波器的三個維度具有不同的通阻特性，則根據具體要求可選擇不同組合種類。

在接下來的小節，我們把三維線性相位FIR濾波器組的設計問題寫出極小化極大值問題，帶入約束凸規劃求解。

3 線性相位3D FIR數字濾波器的設計

基于CVX工具箱的約束凸規劃法（DCP），用來求解各類凸問題[21]。與半定規劃（SDP）法和二階錐規劃（SOCP）法相比，DCP對問題描述簡單直觀，求解復雜問題的能力更強。為了采用CVX求解三維線性相位FIR數字濾波器的設計問題，我們先把FIR三維數字濾波器的設計問題表達成極小化極大值問題：

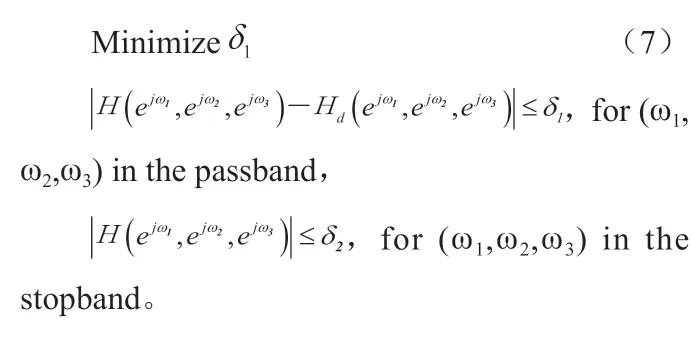
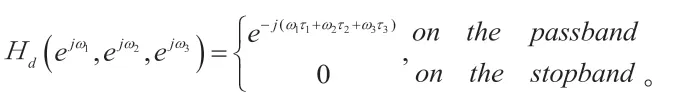
采用DCP設計FIR一維或二維數字濾波器時，問題描述相同。唯一不同的是在（7）式中待求未知變量數是三維變量。在濾波器每維度系數長度一樣時FIR三維數字濾波器的待求變量是一維數字濾波器的倍。式（7）可以用來求任意相位響應的FIR濾波器。對于線性相位FIR濾波器，可以利用其濾波器系數的對稱性，來降低待求變量數。只是對于表1中的不同組合形式，式5要做不同的改寫。例如組合111，式（7）改寫如下：

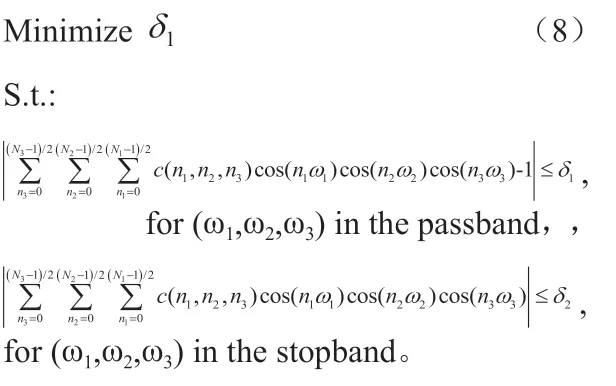
4 三維線性相位FIR數字濾波器的設計實例

設計三維線性相位FIR數字濾波器時，必須預先了解以下幾點：

（1）所期望的濾波器單位脈沖響應長度；

（2）所期望的濾波器分段頻率特性（低通、高通等）及截止頻率點；

（3）所期望的濾波器通帶/阻帶形狀（球形、立方形等）；

（4）所期望的濾波器通帶或阻帶所能接受的最大波紋誤差。

一般來說，濾波器系數的長度、過渡帶寬度（通帶與阻帶之間的間隔）和通帶、阻帶上的波紋誤差之間是一種相互制衡的關系。濾波器系數越長，過渡帶越寬，則通帶和阻帶波紋誤差則越小。而通帶和阻帶波紋誤差之間也有相互制衡的關系，壓縮通帶的波紋誤差，也就是要獲得更好的通帶平坦性，則在其他參數不變的前提下，必然以增大阻帶波紋誤差作為代價。

例1：設計一個長度(5，5，5)，球面對稱，線性相位的低通FIR三維數字濾波器。通帶截止頻率和阻帶截止頻率分別為（0.3π，0.6π），濾波器的阻帶最大波紋誤差設為-30dB。把濾波器設計問題寫成式（8）進行求解。待求系數c(n1,n2,n3)大小為（3×3×3）個。圖1中顯示其幅度頻率響應。

由于所得濾波器在三個維度方向上具有對稱性，從另外兩個維度看進去的濾波器幅頻特性與圖1中是一致的。其濾波器系數列于表2中，以供讀者參考。仔細觀察表2中數據，可發現每頁數據具有關于對角線對稱的特性；并且第一頁第二列數據與第二頁第一列數據相同，以此類推。表2中濾波器系數的對稱性緣于本例中所要求設計的濾波器在三個維度上通阻帶截止頻率點相同，濾波器長度一致，即濾波器在幅頻上具有對稱性。這種幅頻對稱特性也可以用來降低濾波器設計過程的未知變量數。但這種幅頻對稱特性在單位脈沖響應上的影響較為復雜，尤其是濾波器比較長的時候。例2：設計一個長度(12，12，12)，通帶區域方形對稱，線性相位的低通FIR三維數字濾波器。通帶截止頻率和阻帶截止頻率分別為（0.3π，0.6π），濾波器的阻帶最大波紋誤差設為-30dB。待求系數c(n1,n2,n3)大小為63個。圖2顯示的是所得三維FIR數字濾波器幅頻響應圖，其在通帶的最大波紋誤差為2.048e-3。由于篇幅所限，濾波器系數沒有列出來。

5 結束語

在處理三維數字信號時，考慮到數據之間的相關性，三維數字濾波器的設計不可避免。三維數字濾波器設計工作的難點在于龐大的待求未知變量數。本文從一維線性相位FIR濾波器系數的對稱性出發，首次提出三維線性相位FIR濾波器共有20種不同類型。利用濾波器系數的對稱性，大幅度減少濾波器設計過程中待求未知變量淑，把三維線性相位FIR數字濾波器的設計問題寫成極大值極小化問題，帶入凸規劃求解。實驗結果顯示，這種方法可以獲得具有良好頻率特性的三維線性相位FIR濾波器。