風力機攻角與錐角優化及其相關性探討*

趙 騫， 厲 偉， 姚興佳， 邵一川， 郭慶鼎

(1. 沈陽工業大學 電氣工程學院， 沈陽 110870； 2. 沈陽大學 信息工程學院， 沈陽 110004)

本文對風力機葉片攻角α及風輪錐角β進行優化，并對α與β之間的相關性做進一步研究，為進一步設計新型更高效風力機提供最佳的優化方案.采用兩套優化方案對NACA0012翼型的1.5 MW風力機α、β角進行實例優化，方案1對α、β進行獨立優化：首先應用傳統葉素動量(BEM)理論對葉片攻角α進行優化，確定α的最佳工作點，再在該最佳工作點處，應用對β錐角修正所得的β-BEM理論進一步對錐角β進行優化，計算優化后風能利用系數Cp1.方案2對α、β角進行統一優化：應用β-BEM理論同時對α、β角進行優化，計算優化后風能利用系數Cp2.通過對Cp1與Cp2進行對比分析，研究α、β之間相關性，并確定最佳優化方案.

1 傳統葉素動量理論

1.1 貝茨理論模型

圖1為Betz理論的氣流圖.在風輪上游遠端處，風速為υ0，氣流截面積為S0；風輪處，風速為υ，氣流截面積為S；風輪下游遠端處，風速為υ1，氣流截面積為S1.由Betz理論[6]可知，當滿足式(1)，即

(1)

(2)

式中，ρ為空氣密度.風力機工作于低風速環境下，此時氣流視為不可壓縮流體，式(1)結合連續性方程S0υ0=Sυ=S1υ1得

S0∶S∶S1=1∶2∶3

(3)

式(3)說明風輪上、中、下游的氣流截面積逐漸增大，表明在風輪處氣流除具有平行于風輪旋轉軸的軸向速度外，同時具有垂直于旋轉軸的徑向速度分量，這為進一步引入風輪錐角β提供了依據.

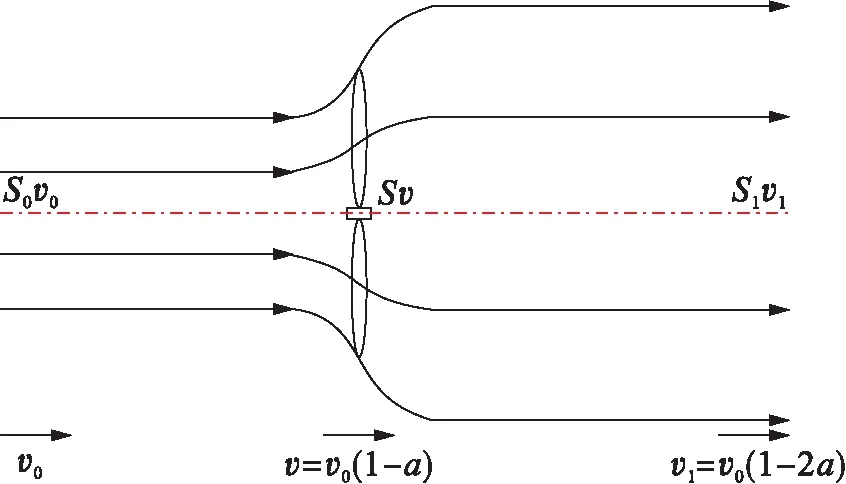
圖1 貝茨理論風輪氣流圖Fig.1 Airflow of wind wheel in Betz theory

1.2 傳統葉素動量理論

葉素動量理論一直是研究風力機氣動特性的有效方法，相關研究在文獻中多有報道[7-9].傳統的葉素動量理論采用零錐角模型(β=0°)，即風輪旋轉面與旋轉軸垂直，此時風輪處氣流的徑向速度分量與旋轉面平行，對風輪不產生轉矩作用，因此只考慮氣流軸向速度對風輪產生的轉矩作用.

由動量理論可知，氣流作用在風輪根部距離r處時葉素的軸向推力dFn和轉矩dM分別為

(4)

dM=4πρωυ0a′(1-a)r3dr

(5)

式中：a為軸向誘導因子；a′為周向誘導因子；ω為轉速.同時，由葉素理論可得到

(6)

(7)

式中：Nb為葉片數；c為葉素弦長；CL、CD為風力機翼型升力、阻力系數；φ為入流角，其表達式為

(8)

式中，λ為當地速度比，其表達式為

(9)

對于某確定的翼型，CL、CD主要由攻角α決定，其表達式為

α=φ-θ

(10)

式中，θ為節距角.

分別將式(4)、(6)及式(5)、(7)建立等量關系，并引入普朗特葉尖損失因子f，可計算出軸向誘導因子a及周向誘導因子a′為

(11)

(12)

式中，σ為實度，其表達式為

(13)

進一步結合式(2)、(7)計算出風能利用系數為

Cp=σλ[(1-a)2+λ2(1+a′)2]·

(CLsinφ-CDcosφ)

(14)

給定當地速度比λ及節距角θ，通過迭代式(8)～(13)計算出a、a′的收斂值，并進一步由式(14)計算出風能利用系數Cp.

2 基于錐角β的BEM修正理論

傳統BEM理論模型中沒有涉及到錐角β，因此，若要對β實現優化，須對傳統BEM理論進行β修正.圖2為將β引入到傳統葉素動量理論后的氣流分布示意圖，此時風輪旋轉面為圓錐面，氣流在與旋轉軸垂直平面內的徑向速度分量與風輪旋轉圓錐面不平行，因此，徑向速度分量亦將對風輪產生轉矩作用，進而轉換為風輪輸出功率.

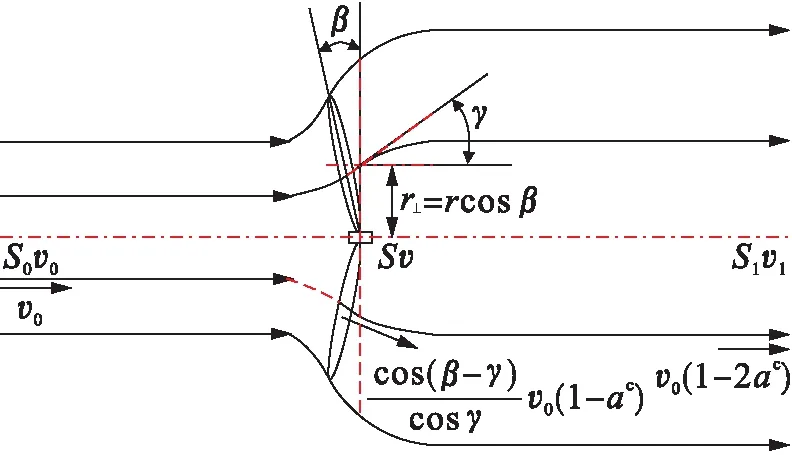
圖2 β錐角時風輪氣流分布Fig.2 Airflow distribution of wind wheel with cone angle β

如圖2所示，取與葉根距離為r的風輪葉素，其距離旋轉軸的垂直距離為

r⊥=rcosβ

(15)

氣流速度與風輪旋轉錐面垂直的速度分量υ⊥為

(16)

式中：γ為氣流發散角，表示氣流流線與旋轉軸夾角；ac為對軸向誘導因子a的修正值.

將修正式(15)、(16)及β代入傳統BEM理論表達式(4)～(14)中，得到修正后β-BEM理論表達式為

(17)

dMc=4πρωυ0a′c(1-ac)r3cos4βdr

(18)

CDsinφc)cosβdr

(19)

CDcosφc)rcos2βdr

(20)

(21)

(22)

αc=φc-θ

(23)

(24)

(25)

(26)

(CLsinφc-CDcosφc)

(27)

β-BEM理論表達式(17)～(27)在風輪錐角β=0°時與修正前表達式(4)～(14)完全一致，說明β-BEM理論表達式具有較強的通用性.

3 α、β獨立優化

3.1 NACA0012翼型風力機的α優化

為實現方案1中對α的優化，采用BEM理論對NACA0012翼型的1.5 MW風力機CP值進行數值計算.該翼型為NACA經典翼型，低風速時，該翼型的特性曲線如圖3所示，在小攻角段，CL與α幾乎成正比關系，在12°攻角時翼型發生失速，通常情況下，翼型均工作在失速點之前.

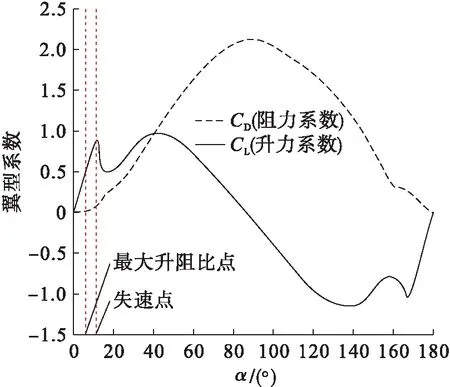
圖3 NACA0012翼型特性曲線Fig.3 Characteristic curves of NACA0012 airfoil

選取翼型中部葉素作為計算區域時，不涉及葉尖損失，因此葉尖損失因子f取1.將λ、θ做為循環變量，對于每一組λ、θ，通過式(8)～(13)迭代求解各參數，進一步代入式(14)計算CP，最終得到CP隨λ、θ變化的曲面圖.使用C++語言編寫該迭代程序，對6萬組λ、θ點的CP值進行計算，近似得到了CP與λ、θ之間的連續變化關系如圖4所示.曲面最高點處λopt=4.02，θopt=4.0°，CP-opt=0.482，攻角αopt=5.9°，該點即為最佳工作點，αopt即為最佳攻角(opt下標表示最佳工作點).

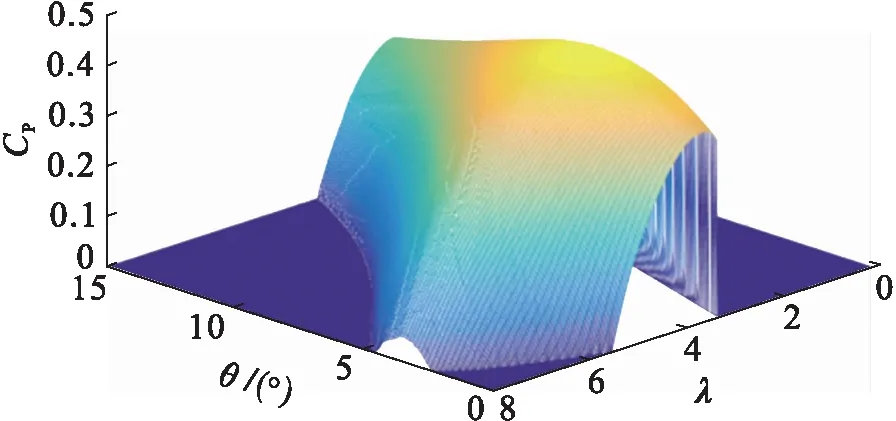
圖4 CP、λ、θ曲面圖Fig.4 Surface diagram of CP，λ and θ

進一步將采用最佳工作點與采用最大升阻比工作點的CP值做比較.在圖4中分別提取攻角α等于最佳攻角(α=αopt=5.9°)和最大升阻比攻角(α=αmldr=4.2°)的各數據點，構成兩條等攻角曲線，分別稱之為最佳攻角曲線和最大升阻比攻角曲線，兩者對比圖如圖5所示.

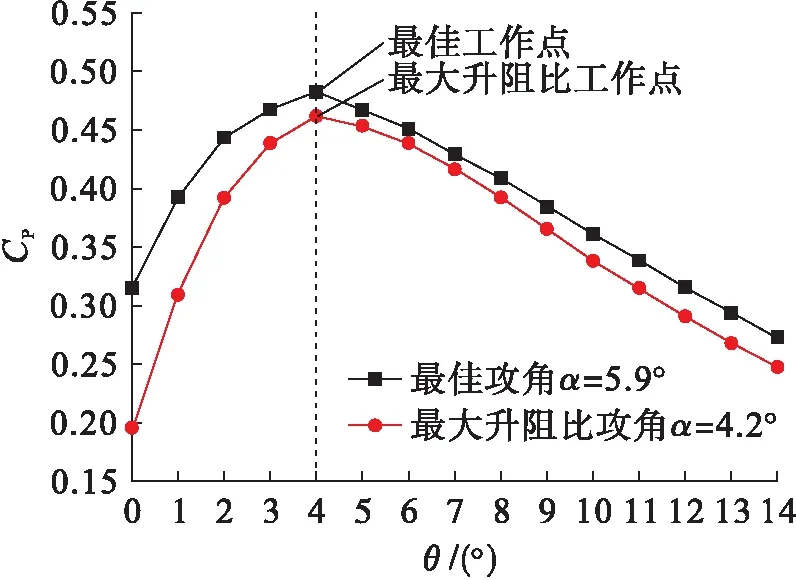
圖5 最佳攻角與最大升阻比攻角時CP對比Fig.5 Comparison of CP at optimum attack angle andattack angle with maximum lift-drag ratio

由圖5可見，在其它因素相同的條件下，采用最佳攻角比采用最大升阻比攻角的CP值顯著提高.兩曲線CP值均在θ=4°時達到極大值，兩極值點分別稱為最大升阻比工作點和最佳工作點，對應CP值分別為0.462 0和0.482 1.可見最佳工作點比采用最大升阻比工作點時，CP提高了4.3%.

計算結果同時表明，采用最佳工作點時，當地速度比λ由原采用最大升阻比工作點時的4.7降為4.0，減小15%.這說明在不改變風輪其它運行參數的條件下，轉速降低15%，可使風力機由最大升阻比工作點調整到最佳工作點.

3.2 NACA0012翼型風力機的β優化

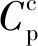
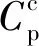
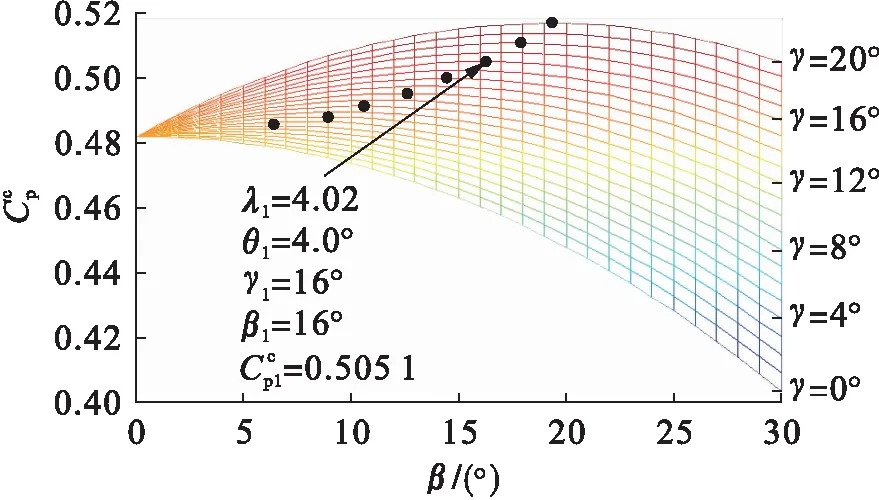
圖6 α、β獨立優化曲線簇Fig.6 Curve cluster of after independent optimization of α and β

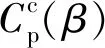
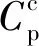
4 α、β的統一優化

為實現優化方案2中對α、β的統一優化，將β、γ、λc、θ四參數在迭代程序中進行統一考慮.程序流程圖如圖7所示.

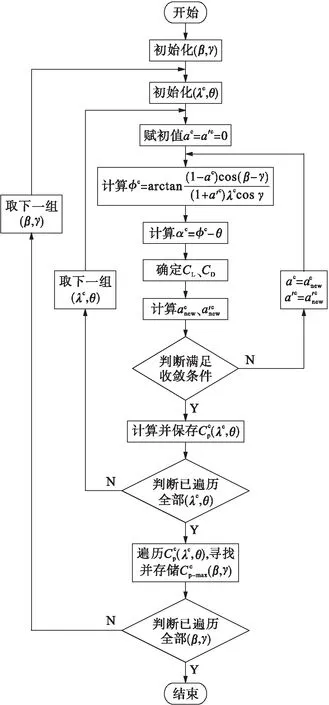
圖7 α、β統一優化程序流程圖Fig.7 Flow chart of procedure for unified optimization of α and β

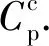
圖8 α、β統一優化曲線簇Fig.8 Curve cluster of after unified optimization of α and β

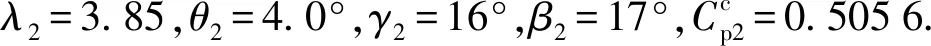
5 結 論

分別采用對α、β的獨立優化方案和統一優化方案對NACA0012翼型的1.5 MW風力機α、β角進行實例優化，結果表明：

1) 采用α最佳工作點攻角與采用最大升阻比工作點攻角相比，在其它因素相同的情況下，風力機Cp提高4.3%；在α最佳工作點處繼續對β優化，Cp再提高4.8%.

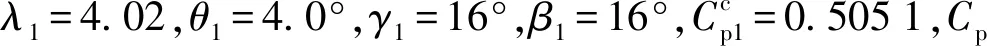
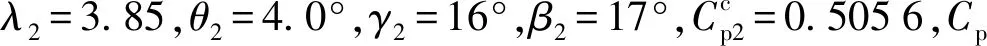
α、β具有弱相關性，理論上宜采用統一優化方案，但由于Cp提升率差異不大，故從工程方便角度考慮，仍可以采取獨立優化方案.