改進GM(1，1)模型對地鐵開挖沉降的預測*

戴文亭， 王 振， 王宇放， 王 琦

(吉林大學 交通學院， 長春 130022)

城市地鐵在施工過程中會對土層造成一定程度上的擾動，從而引起地表沉降，此外，由于城市中建筑密集、地下管線密布、施工條件受限，地表沉降較難控制，因此，滿足一定精度的隧道施工引起的地面變形預測方法愈加受到關注[1]，已有很多學者就此問題進行了研究[2-3]，有限元軟件也逐漸開始應用到地表沉降預測[4]，而灰色系統理論以其數據少、預測精度高和無需先驗信息的特點逐漸受到人們的關注[5]，且在各行業均有應用.

本文討論了建立新陳代謝GM(1，1)模型過程中最佳原始序列的個數，并采用多種方式對原模型進行改進，結合改進模型的預測值對改進模型的適用范圍進行了討論.

1 灰色系統理論

1.1 GM(1，1)模型建立過程

均值GM(1，1)模型(以下簡稱GM(1，1)模型)是鄧聚龍教授最先提出的灰色預測模型，也是目前影響最大，應用最為廣泛的模型，模型建立過程[10]如下：

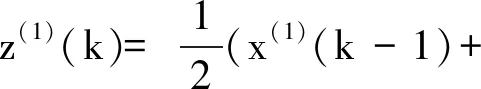
1.2 GM(1，1)模型局限性

1) 原始序列越平順則模型預測越準確[11]，若原始序列上下波動較大則模型預測精度將會降低，原始序列越接近指數函數的分布則模型預測越準確，若原始序列與指數函數的分布相差越大則模型預測準確度越差，因此，在建模過程中要注意原始數據段的選取并需要及時更新數據.

2) 原始模型中背景值由均值生成的Z(1)(k)來代替，而GM(1，1)模型擬合曲線為指數曲線，因此，在區間[k，k+1]上曲線的實際面積要始終小于abcd所未成的梯形面積，如圖1所示.其中，x(1)(t)為由GM(1，1)模型擬合曲線的指數函數；x(1)(k)為擬合的指數函數在k處的取值.若原始序列增長速率較慢則兩者相差不多，但當原始序列變化急劇時，兩者面積差ΔS變大，若仍用Z(1)(k)代替則模型偏差較大，而且為滯后誤差.

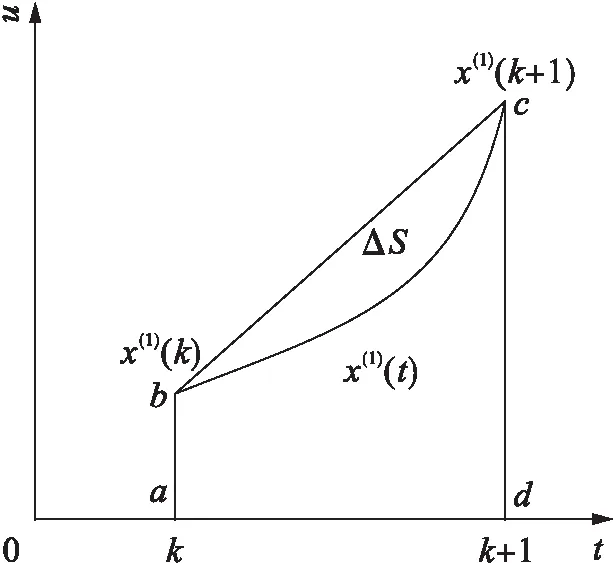
圖1 背景值構造示意圖Fig.1 Schematic establishment of background values

2 改進灰色系統理論

隨著灰色系統理論的不斷發展，研究人員在原始模型的基礎上不斷進行改進優化，對于GM(1，1)的優化改進主要有以下幾種方法：改變原始序列的平順度；改變模型背景值；組合模型.組合模型類型較多，例如與神經網絡結合，與時間序列結合等，在此不再贅述.

2.1 最佳原始序列個數

根據灰色系統的基本原理，新信息優先原理，即新信息對認知的作用大于老信息，在建立模型過程中一般采用新陳代謝GM(1，1)模型.新陳代謝模型建立時一般取4～8個數據作為原始序列，在出現新的數據后將其放入原始序列中，并將“老”的信息去掉，最后再進行下一次預測，保證模型中數據個數始終不變.從預測角度分析，新陳代謝模型是最理想的模型，系統在發生變化過程中老的數據已經無法反映系統當前特征，去掉是完全合理的，而且老數據的去除也能減少計算量.取長春地鐵二號線暗挖區拱頂地表沉降點進行分析，沉降觀測數據如表1所示.

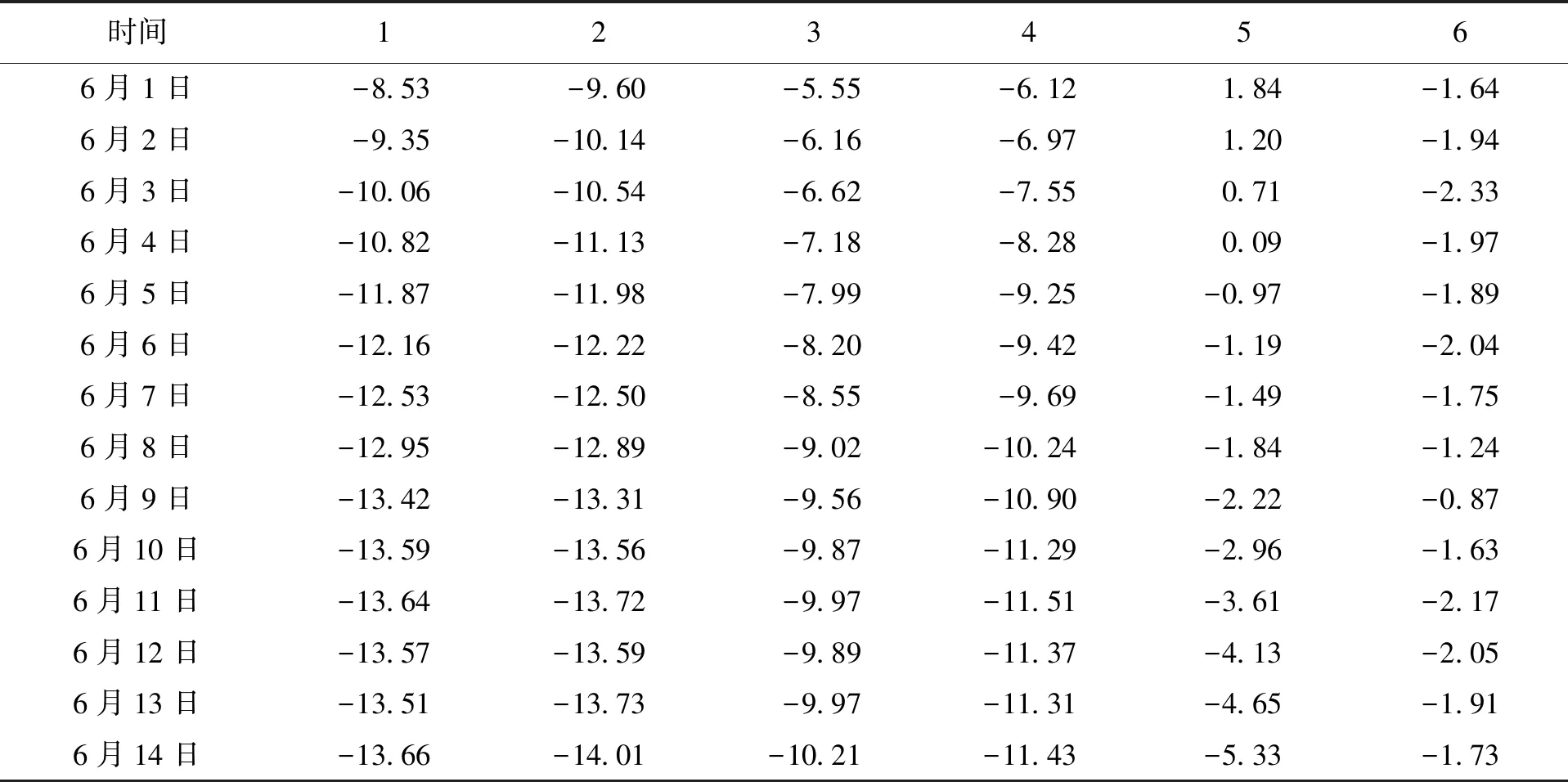
表1 地鐵二號線暗挖區拱頂地表沉降Tab.1 Ground surface settlement of vault of metro line 2 undermining area mm

取1號、2號沉降觀測點進行分析，根據6月1日～6月10日的累計沉降量對6月11日～6月14日的累計沉降量進行預測，分別取3～8個點(3個點，即6月8～10日，4個點，即6月7～10日，其余依次向前加一天)作為原始序列建立新陳代謝GM(1，1)模型，分別命名為模型3，模型4，，模型8，預測結果及誤差如表2所示.

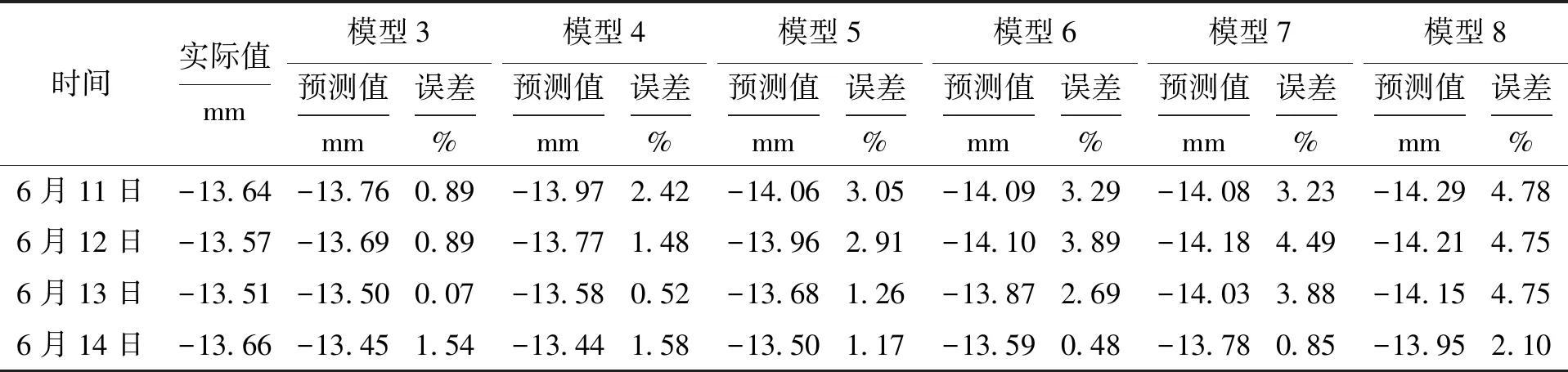
表2 各個GM(1，1)模型對1號點累計沉降量的預測Tab.2 Prediction of cumulative settlement of point 1 in each GM (1，1) model

各個模型預測值的平均誤差分別為0.847%、1.500%、2.098%、2.590%、3.112%、4.092%，隨著所取點數的增加，平均誤差不斷增加，實際值與預測值如圖2所示.由表2和圖2可知，取模型3的預測值與實際值相比無論是在整體走勢、預測值上均比較接近，且在與另外幾個新陳代謝GM(1，1)模型相比，其平均誤差最小，但是該模型對6月14日預測的誤差較大且變化趨勢與實際相反，這主要是因為實際的累計沉降量曲線在該處變化不平順.表3為各個GM(1，1)模型對2號點累計沉降量的預測.

與1號點類似，各個模型預測值的平均誤差分別為1.445%、1.755%、1.953%、2.210%、2.170%、2.729%，隨著所取點數的增加，平均誤差不斷增加，實際值與預測值如圖3所示.

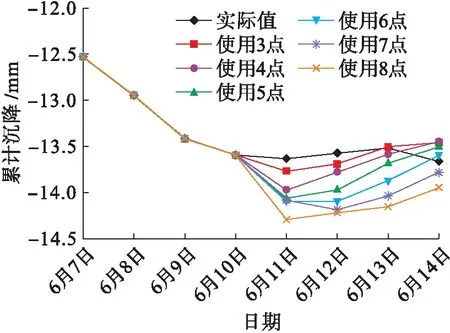
圖2 1號點累計沉降實際值與預測值Fig.2 Measured and predicted values of cumulative settlement of point 1

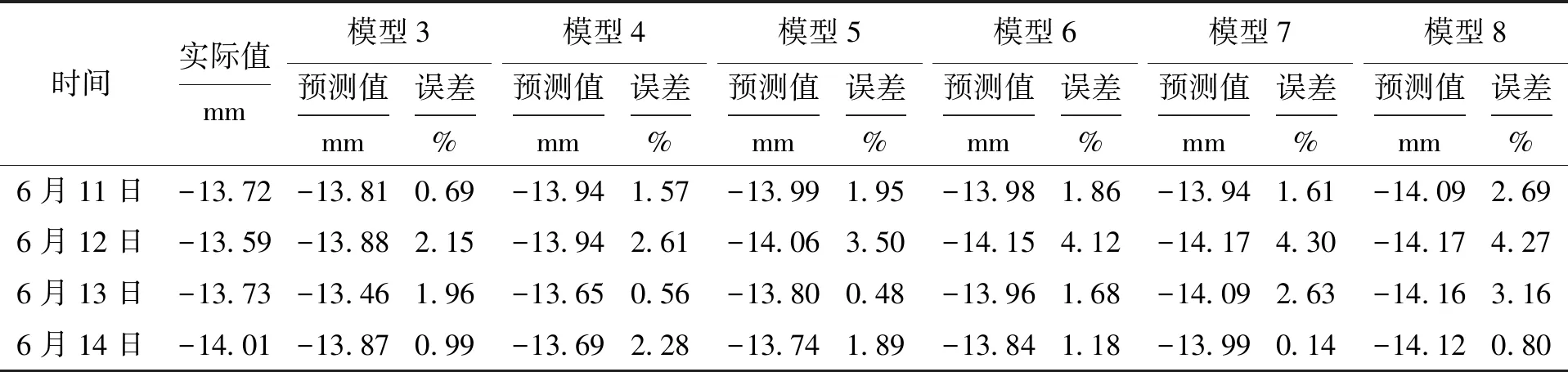
表3 各個GM(1，1)模型對2號點累計沉降量的預測Tab.3 Prediction of cumulative settlement of point 2 in each GM (1，1)model

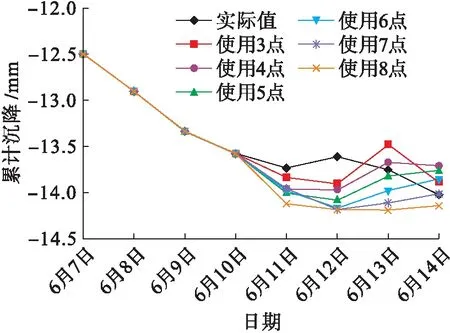
圖3 2號點累計沉降實際值與預測值Fig.3 Measured and predicted values of cumulative settlement of point 2

由表3和圖3可知，取3點建立的新陳代謝GM(1，1)模型的預測值與實際值相比，6月11日～6月13日走勢相反，而且對6月13日的預測偏差較大，這主要是因為實際累計沉降量變化不平順且趨勢不斷變化.采用同樣的方法對5號點、6號點進行處理，實際值與預測值如圖4、5所示.

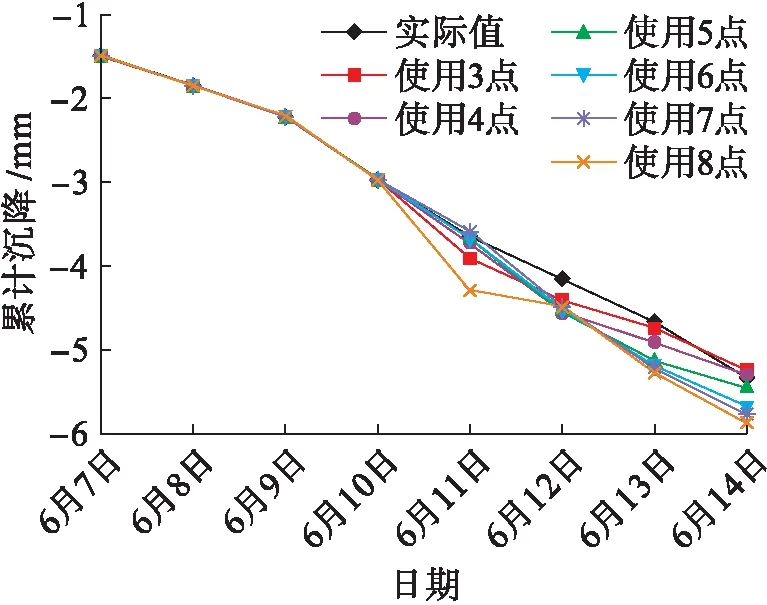
圖4 5號點累計沉降實際值與預測值Fig.4 Measured and predicted values of cumulative settlement of point 5

對比分析模型3對5號點、6號點的預測可知，當原始序列變化平順時除了模型8之外各個模型預測值雖然有優有劣，但是相差不大，當原始序列較為曲折時，各個模型的預測值相差變大.通過對比分析各個新陳代謝模型對以上4個點的預測可以發現，相對其他模型，模型3平均誤差相對較小，且對數據變化特別敏銳，但是當在某次出現極值時，對下一次預測模型的趨勢和精度均會出現誤差，尤其是連續出現極值時誤差與預測趨勢偏差更大，如模型對2號點和6號點累計沉降量的預測，當不出現極值時模型3對原始數據的預測一般會偏大.

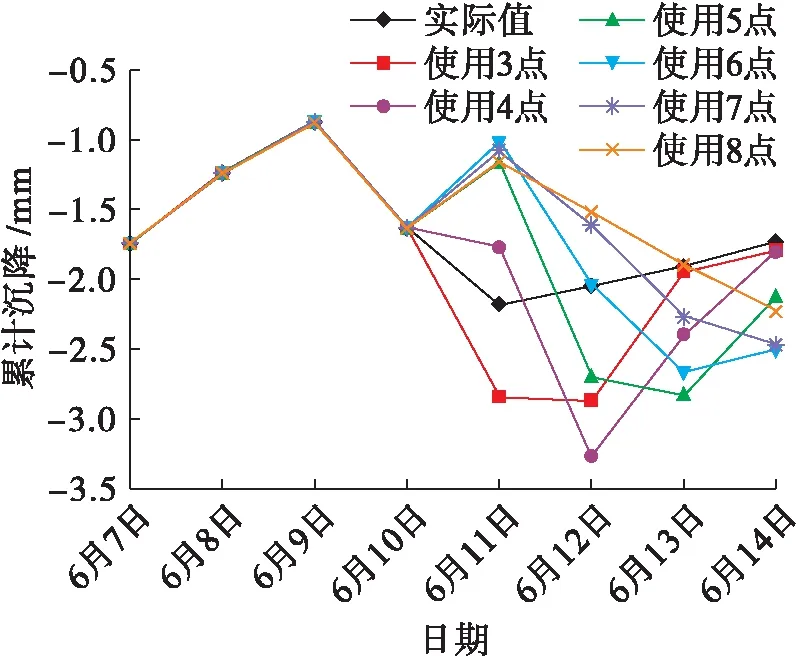
圖5 6號點累計沉降實際值與預測值Fig.5 Measured and predicted values of cumulative settlement of point 6

灰色系統理論在處理小容量樣本、貧信息、不確定系統方面有較強優勢，原始序列較少時更能體現出灰色系統理論的優勢，使用“新陳代謝”模型使預測模型更具有時效性，因此，在數據較少情況下平均誤差相對較小.

2.2 原模型的優化

根據GM(1，1)模型的局限性，對模型的改進主要有兩種方式：一種是改變原始序列的平順度，使序列變得平順從而減小預測；另一種是改變建立模型時的背景值Z(1)(k)，從而提高預測精度.

根據上述思路對新陳代謝GM(1，1)模型進行改進，取原始序列的緩沖算子作為原始序列，然后構建新的模型，對累計沉降量進行預測，改變背景值的構造方法，使模型更加接近實際走勢.

模型1當模型變化趨勢不變時，預測值總比實際值大，取弱化緩沖算子比較合理，取平均弱化緩沖算子(AWBO)對原始序列進行處理，再根據前文方法建立新陳代謝GM(1，1)模型.AWBO的定義如下：

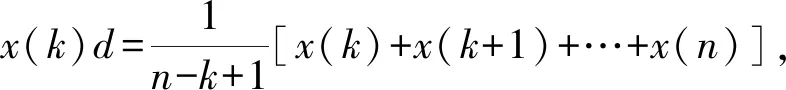
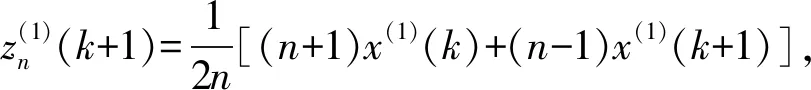
式中：N為原始序列長度；Ri=x(1)(i)/x(1)(i-1)，i=2，3，，N.

模型3將上述兩個模型進行整合，先按照模型1的方法得出緩沖算子序列并作為新的原始序列，再采用模型2中的方法構造背景值.

使用模型1～3分別對1號點進行預測分析，預測結果與誤差如表4所示.

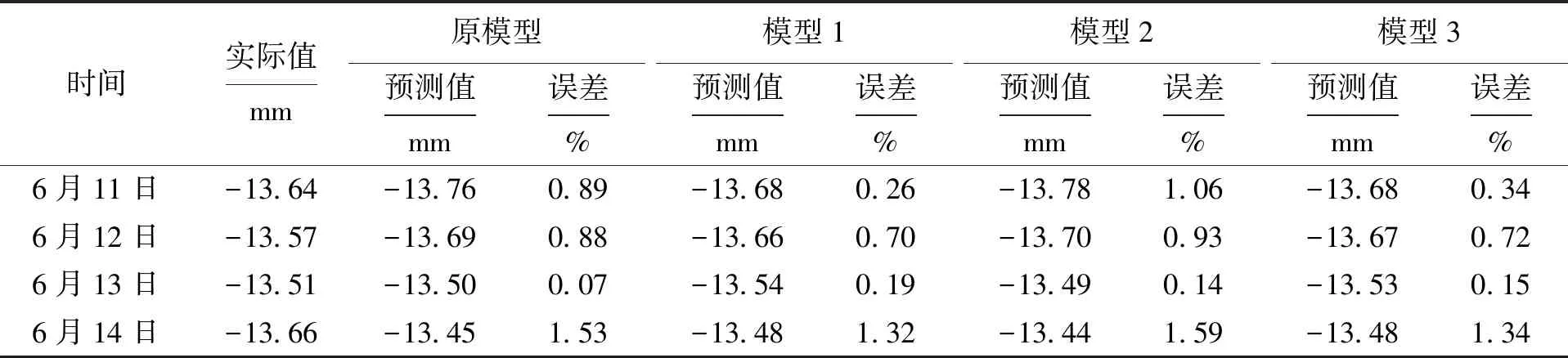
表4 各個模型對1號點的預測值及誤差Tab.4 Predicted values and errors of point 1 in each model

表4中4種模型的平均相對誤差分別為0.847%、0.616%、0.931%、0.641%，模型1的平均相對誤差最小，其次是模型3，而模型2的誤差比原模型的誤差大.實際值與預測值如圖6所示.表5為各個模型對2號點的預測值及誤差.

表5中4種模型的平均相對誤差分別為1.445%、1.196%、1.544%、1.183%，模型3的平均相對誤差最小，其次是模型1，而模型2的誤差比原模型的誤差要大.實際值與預測值如圖7所示.

通過分析各個模型對1號點、2號點累計沉降量的預測可知，背景值的改變并不能改變模型對地鐵開挖時產生累計沉降量預測的精度，且相比對緩沖算子的影響，預測值的改變量要小得多.

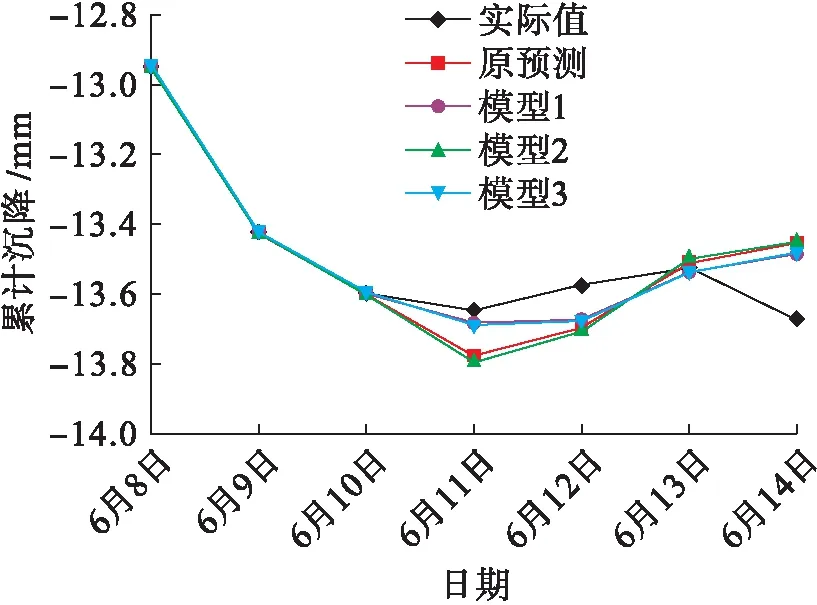
圖6 模型優化后1號點累計沉降實際值與預測值Fig.6 Measured and predicted values of cumulative settlement of point 1 after model optimization

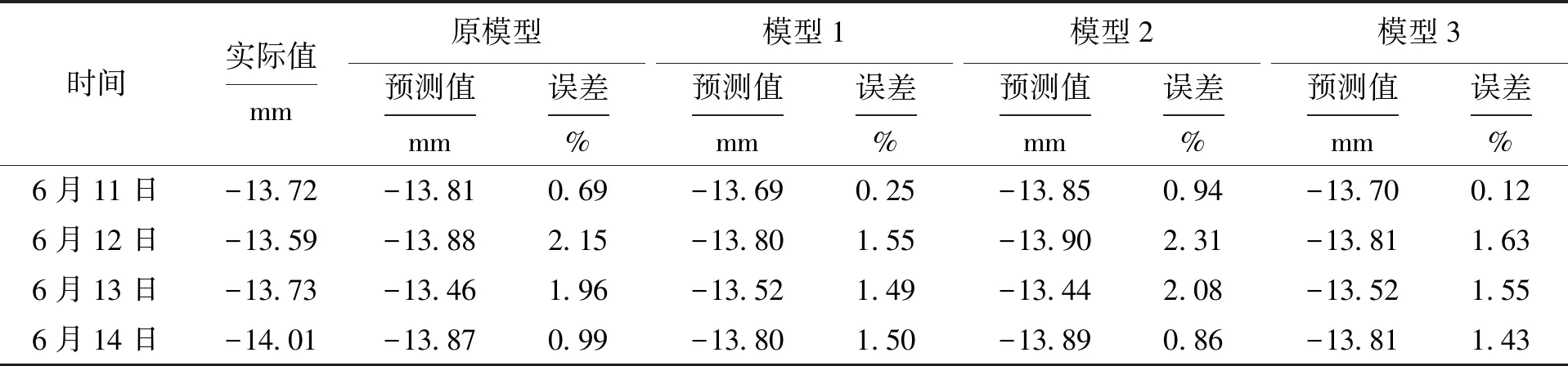
表5 各個模型對2號點的預測值及誤差Tab.5 Predicted values and errors of point 2 in each model

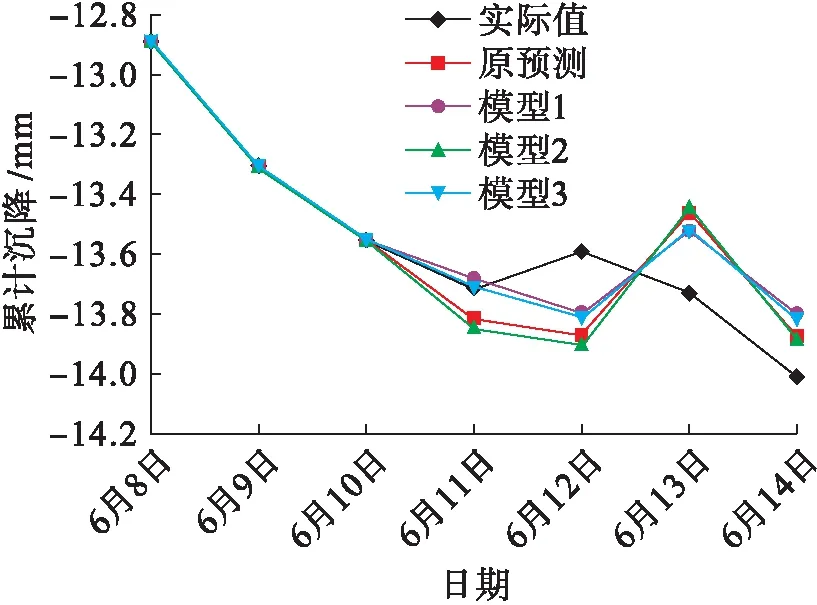
圖7 模型優化后2號點累計沉降實際值與預測值Fig.7 Measured and predicted values of cumulative settlement of point 2 after model optimization

圖8、9為5號點、6號點累計沉降實際值與預測值.對比分析各個模型對5號點和6號點的預測可知，當原始序列變化平順時，各個模型的預測值相差不大，緩沖算子對提高測量精度作用不明顯，甚至會使預測出現更大偏差.但當模型較為曲折時，模型1和模型3對預測精度的提高相當明顯.通過以上分析可知，緩沖算子改進模型對不平順原始序列的預測精度要高于原預測模型的精度，但對平順原始序列的改進效果則不太明顯.

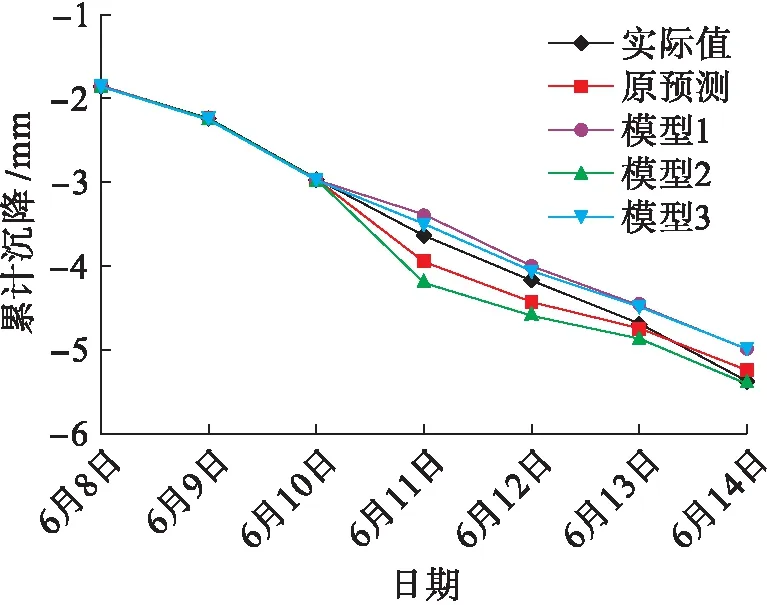
圖8 模型優化后5號點累計沉降實際值與預測值Fig.8 Measured and predicted values of cumulative settlement of point 5 after model optimization

3 結 論

本文使用灰色系統理論對地鐵暗挖區拱頂地表沉降量進行預測，并提出如下改進方法：

1) 對模型取用原始序列中數據個數進行了研究，對比取用3～8個數據時的預測精度，得出了最優取用個數.

2) 結合灰色模型本身局限性對新陳代謝GM(1，1)模型進行優化，通過對比分析可知，背景值優化對模型預測值影響較小；緩沖算子優化在原始序列變化較大、變化不平順時優化較好，但如果原始序列變化平順則其優化效果不好.

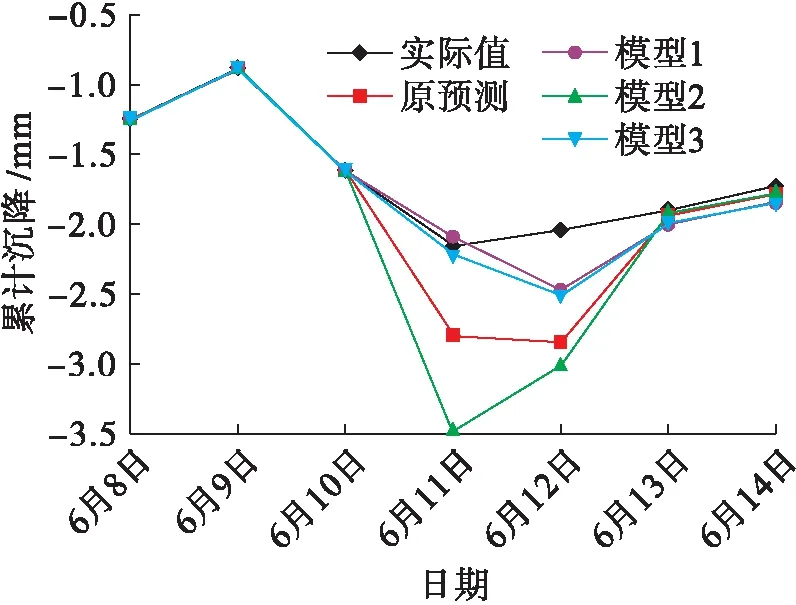
圖9 模型優化后6號點累計沉降實際值與預測值Fig.9 Measured and predicted values of cumulative settlement of point 6 after model optimization