PCA-改進(jìn)RPROP方法的BP算法在音樂信號(hào)分類中的應(yīng)用
(1.青島大學(xué) 機(jī)電工程學(xué)院,山東 青島 266071; 2.青島大學(xué) 商學(xué)院,山東 青島 266071)
傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)采用梯度修正法作為權(quán)值和閾值更新的方法,僅從預(yù)測(cè)誤差負(fù)梯度方向修正權(quán)值和閾值,學(xué)習(xí)過(guò)程收斂緩慢,并且容易陷入局部最小值,導(dǎo)致泛化能力不足[1-4]。為了解決在此方面的問(wèn)題,朱江森[5]等人提出一種應(yīng)用在氫原子鐘鐘差預(yù)測(cè)上的改進(jìn)BP神經(jīng)網(wǎng)絡(luò),通過(guò)加入誤差懲罰項(xiàng)的措施,減小了平均預(yù)測(cè)誤差,提高了預(yù)測(cè)精度并減少了收斂時(shí)間。Zweiri[6]等人提出三項(xiàng)BP算法,除了學(xué)習(xí)速率和動(dòng)量因子外,添加了第3個(gè)權(quán)重調(diào)節(jié)參數(shù),從一定程度上改善了收斂速度慢和易陷入局部最小值導(dǎo)致的泛化能力不足的問(wèn)題。文獻(xiàn)[7]~文獻(xiàn)[9]也分別提出了改善BP算法的方法,但是這些算法均是基于梯度大小改變權(quán)值和閾值的方式,雖然可以通過(guò)在梯度方面加入?yún)?shù),但實(shí)質(zhì)很難避免偏導(dǎo)數(shù)大小對(duì)網(wǎng)絡(luò)收斂速度和網(wǎng)絡(luò)的泛化能力的絕對(duì)影響。而Resilient Backpropagation[10](RPROP)方法是一種基于偏導(dǎo)數(shù)正負(fù)改變權(quán)值的方法,可以有效改善偏導(dǎo)數(shù)大小對(duì)網(wǎng)絡(luò)收斂的影響。楊存祥[11]等人利用RPROP 法改善BP神經(jīng)網(wǎng)絡(luò),建立了異步電動(dòng)機(jī)故障診斷模型,相比標(biāo)準(zhǔn)BP算法診斷精度和網(wǎng)絡(luò)的訓(xùn)練速度都明顯加快。文獻(xiàn)[12]和文獻(xiàn)[13]分別在BP網(wǎng)絡(luò)中應(yīng)用了RPROP方法,但是這些算法均是對(duì)RPROP方法的直接應(yīng)用,并沒有對(duì)RPROP方法做出改進(jìn)。
基于梯度大小更新權(quán)值和閾值的方式確實(shí)很難回避偏導(dǎo)數(shù)大小對(duì)網(wǎng)絡(luò)收斂速度的影響,但是計(jì)算出梯度馬上利用梯度進(jìn)行權(quán)值和閾值的更新讓算法比較簡(jiǎn)練,而且只需存儲(chǔ)網(wǎng)絡(luò)下一次更新的梯度,消耗的存儲(chǔ)空間較小。RPROP方法是一種基于偏導(dǎo)數(shù)正負(fù)改變權(quán)值的方法,偏導(dǎo)數(shù)的大小并不影響網(wǎng)絡(luò)的收斂速度,完全避免了偏導(dǎo)數(shù)大小對(duì)網(wǎng)絡(luò)收斂影響。但是由于需要近兩倍于標(biāo)準(zhǔn)算法更新權(quán)值的存儲(chǔ)空間,使基于RPROP的算法對(duì)計(jì)算機(jī)資源消耗較大,特別是在網(wǎng)絡(luò)較復(fù)雜的情況下。近年來(lái)計(jì)算機(jī)硬件的發(fā)展使得存儲(chǔ)空間在一般情況下不會(huì)成為算法的瓶頸,又考慮到網(wǎng)絡(luò)訓(xùn)練中步長(zhǎng)的大小對(duì)網(wǎng)絡(luò)的收斂影響極大,于是為了充分加快網(wǎng)絡(luò)的收斂速度,引入了一種變步長(zhǎng)的方法改善RPROP方法。Harris[14]等人提出的一種變步長(zhǎng)的方法被認(rèn)為是最有效的改變的方法,該方法需要根據(jù)多次網(wǎng)絡(luò)更新用到的偏導(dǎo)數(shù)情況來(lái)確定步長(zhǎng)的大小,同時(shí)該算法保留了合適的振蕩幅度,在加快收斂的同時(shí)很好地避免了陷入局部最小值問(wèn)題。本文將兩種算法進(jìn)行融合,改進(jìn)RPROP方法。同時(shí)考慮到網(wǎng)絡(luò)參數(shù)的數(shù)量對(duì)網(wǎng)絡(luò)的收斂速度和訓(xùn)練所消耗的計(jì)算機(jī)資源有直接影響,為減少網(wǎng)絡(luò)的非必要參數(shù),本文將PCA算法與改進(jìn)后的BP神經(jīng)網(wǎng)絡(luò)結(jié)合,提出了一種PCA-改進(jìn)BP神經(jīng)網(wǎng)絡(luò)算法。對(duì)重金屬音樂、山歌音樂、流行音樂和笛子音樂4種語(yǔ)音信號(hào)進(jìn)行識(shí)別,通過(guò)試驗(yàn)結(jié)果對(duì)比發(fā)現(xiàn),本算法確實(shí)可以達(dá)到加快網(wǎng)絡(luò)收斂速度和提高泛化能力的目的。
1 改進(jìn)的RPROP算法
1.1 變學(xué)習(xí)速率方法
Harris根據(jù)均方誤差的梯度分量符號(hào)來(lái)估計(jì)與最小均方誤差的距離,當(dāng)檢測(cè)到連續(xù)符號(hào)變化時(shí),步長(zhǎng)減小。當(dāng)檢測(cè)到的符號(hào)連續(xù)變化相同時(shí),步長(zhǎng)增加。該算法用均方誤差梯度分量符號(hào)來(lái)估計(jì)與均方誤差全局極小值間的距離,具體算法為
S(n+1)=S(n)×f(λ)
(1)
其中,
(2)
式中,λ為選擇的常數(shù);m0和m1為自己選擇的正整數(shù)參數(shù),實(shí)驗(yàn)證明m0=3,m1=3會(huì)取得良好的實(shí)驗(yàn)效果。
1.2 Resilient Backpropagation(RPROP)方法
RPROP方法是由德國(guó)的Martin Riedmiller 和Heinrich Braun在1993年提出,RPROP方法用來(lái)指導(dǎo)批處理學(xué)習(xí)的學(xué)習(xí)方案,其原理是:若前次和本次兩次更新的偏導(dǎo)數(shù)的方向不同,則本次不論權(quán)重是增加或者減小,權(quán)重的增減幅度都變小;若前次和本次兩次更新的偏導(dǎo)數(shù)方向相同,則本次不論權(quán)重是增加還是減小,權(quán)重的增減幅度都變大。此方法可以加快網(wǎng)絡(luò)的收斂速度,具體算法為
W(t+1)=W(t)+ΔW(t)
(3)
(4)
(5)
式中,0<α<1<β,為自己確定的參數(shù)值。當(dāng)α=0.5,β=1.2,Δt(0)=0,Δtmin=1×10-6,Δtmax=50時(shí),算法可以取得比較好的效果。
1.3 改進(jìn)后的算法
綜合上述幾種算法的優(yōu)點(diǎn),提出一種新的算法,該算法的推導(dǎo)過(guò)程為
W(t+1)=W(t)+ΔW(t)
(6)
(7)
簡(jiǎn)化得
(8)
所以,有
(9)
又因?yàn)?/p>
(10)
定義
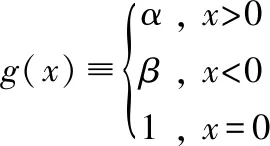
(11)
所以有
(12)
考慮變學(xué)習(xí)率f(λ)的加入,
(13)
使得
(14)
式中,s(t-1)為第(t-1)次學(xué)習(xí)率的步長(zhǎng)。
所以,最終更新的網(wǎng)絡(luò)權(quán)值為
(15)
式中,W(t)為網(wǎng)絡(luò)第t次的權(quán)值;E(t)為網(wǎng)絡(luò)的均方誤差函數(shù);f(λ)為變學(xué)習(xí)速率;g(x)為自定義分段函數(shù):
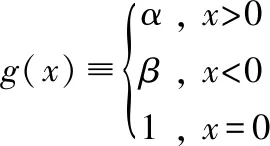
(16)
式中,α=0.5,β=1.2。
2 PCA-改進(jìn)BP神經(jīng)網(wǎng)絡(luò)算法
① 獲取M個(gè)n維的數(shù)據(jù)樣本構(gòu)成M×n的矩陣XM×n,其中每行表示一個(gè)樣本,取前N行用于訓(xùn)練,剩下n-N行用于測(cè)試。所以訓(xùn)練集為XM×N,測(cè)試集為XM×(n-N)。
② 求取訓(xùn)練集XM×N每維的均值為
(17)
③ 對(duì)RM×n進(jìn)行零均值化處理,得
(18)
并且構(gòu)造協(xié)方差矩陣為
(19)
④ 求出協(xié)方差矩陣的特征值λ1≥λ2≥…≥λn及對(duì)應(yīng)的已經(jīng)正交化的特征向量[u1,u2,…,un],其中ui=[ui1,ui2,…uin]。計(jì)算單個(gè)成分貢獻(xiàn)率為
(20)
前i個(gè)貢獻(xiàn)率的和是累計(jì)貢獻(xiàn)率,即
(21)
如果γ≥a(取a=85%)時(shí),就認(rèn)為前i個(gè)主成分為所求,構(gòu)成了投影向量子空間。
⑤ 主成分的個(gè)數(shù)是i,測(cè)試數(shù)據(jù)向主成分向量進(jìn)行投影,得F=[F1,F2,…,F(xiàn)i],其中Fi為
Fi=ui1Y1+ui2Y2+…+uinYn
(22)
⑥ 對(duì)F進(jìn)行歸一化處理,利用歸一化后的F建立i-p-q層神經(jīng)網(wǎng)絡(luò),其中i,p,q分別為輸入層、隱含層、輸出層神經(jīng)元的數(shù)目,具體根據(jù)題目決定。
⑦ 以所提出的改進(jìn)的RPROP算法作為網(wǎng)絡(luò)訓(xùn)練的權(quán)值更新算法訓(xùn)練網(wǎng)絡(luò)。
⑧ 測(cè)試集數(shù)據(jù)XM×(n-N)向投影向量子空間進(jìn)行投影,并進(jìn)行歸一化處理后,輸入訓(xùn)練好的網(wǎng)絡(luò)進(jìn)行測(cè)試,得到能正確識(shí)別的數(shù)目(n-N)′,網(wǎng)絡(luò)識(shí)別率為
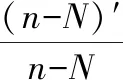
(23)
3 實(shí)驗(yàn)結(jié)果及分析
為了驗(yàn)證算法的有效性,對(duì)音樂分類的問(wèn)題進(jìn)行實(shí)驗(yàn)。采用所提出的PCA-改進(jìn)BP神經(jīng)網(wǎng)絡(luò)和附加動(dòng)量法改進(jìn)的BP神經(jīng)網(wǎng)絡(luò)及標(biāo)準(zhǔn)神經(jīng)網(wǎng)絡(luò)從最高識(shí)別率、達(dá)到最高識(shí)別率90%的用時(shí)和平均識(shí)別率3個(gè)方面進(jìn)行比較。實(shí)驗(yàn)環(huán)境是PC機(jī),Intel Xeon E3-1230 v2 CPU,四核心八線程,主頻3.3 GHz。Windows 10操作系統(tǒng),Matlab 7.1實(shí)驗(yàn)平臺(tái)。
選擇的4類音樂為:重金屬樂,山歌,通俗歌曲,笛子。每類音樂選擇一首樂曲并截取其中1段音樂,4段音樂信號(hào)分別用梅爾頻率倒譜系數(shù)法提取20維語(yǔ)音特征信號(hào)各2000幀,提取的音樂特征信號(hào)如圖1所示。
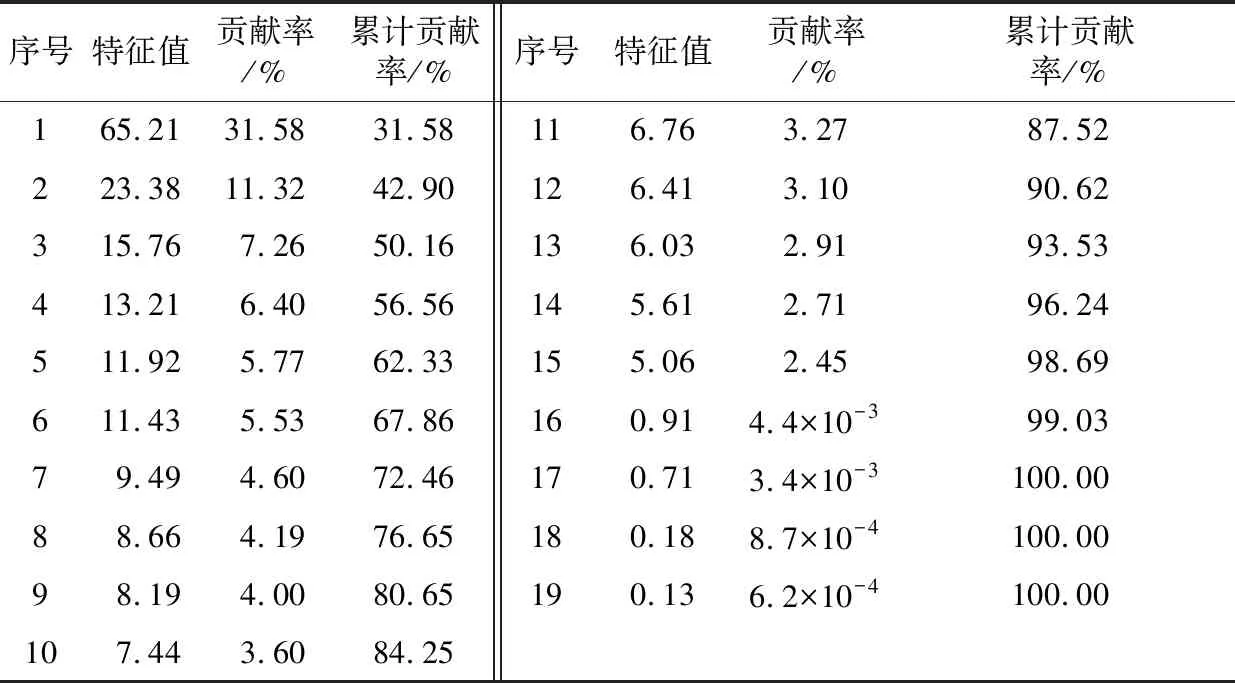
運(yùn)用主成分分析法,對(duì)訓(xùn)練集樣本數(shù)據(jù)R6400×20降維,得到的特征值、貢獻(xiàn)率和累計(jì)貢獻(xiàn)率如表1所示。
由表1可以看出,前11個(gè)特征值的貢獻(xiàn)率為87.52%,所以選擇協(xié)方差矩陣的前11個(gè)特征值對(duì)應(yīng)的個(gè)特征值對(duì)應(yīng)的特征向量組成的空間作為投影空間,對(duì)訓(xùn)練和測(cè)試樣本集數(shù)據(jù)R20×8000進(jìn)行降維,得到R11×8000,之后進(jìn)行歸一化處理。
經(jīng)過(guò)多次嘗試,隱含層節(jié)點(diǎn)數(shù)選擇13時(shí),可以取得比較好的效果。建立11-13-4的BP神經(jīng)網(wǎng)絡(luò),分別用不同的權(quán)值更新方法訓(xùn)練網(wǎng)絡(luò),用測(cè)試樣本進(jìn)行測(cè)試。進(jìn)行50次測(cè)試后,分別找出改進(jìn)后的BP神經(jīng)網(wǎng)絡(luò)和標(biāo)準(zhǔn)梯度下降BP神經(jīng)網(wǎng)絡(luò)能達(dá)到的最高識(shí)別率,最高識(shí)別率對(duì)比如表2所示。
序號(hào)特征值貢獻(xiàn)率/%累計(jì)貢獻(xiàn)率/%序號(hào)特征值貢獻(xiàn)率/%累計(jì)貢獻(xiàn)率/%165.2131.5831.58116.763.2787.52223.3811.3242.90126.413.1090.62315.767.2650.16136.032.9193.53413.216.4056.56145.612.7196.24511.925.7762.33155.062.4598.69611.435.5367.86160.914.4×10-399.0379.494.6072.46170.713.4×10-3100.0088.664.1976.65180.188.7×10-4100.0098.194.0080.65190.136.2×10-4100.00107.443.6084.25
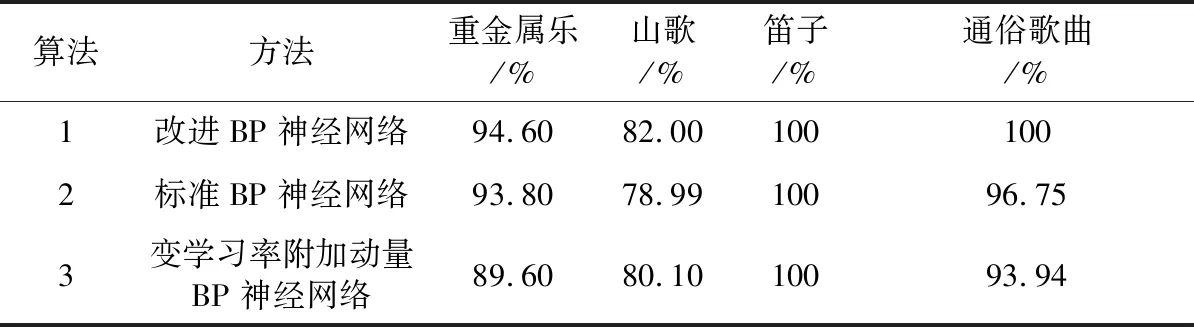
表2 最高識(shí)別率對(duì)比
由表2可以看出,在最高識(shí)別率方面,改進(jìn)的BP神經(jīng)網(wǎng)絡(luò)與標(biāo)準(zhǔn)BP神經(jīng)網(wǎng)絡(luò)相比,對(duì)每類音樂均有更高的識(shí)別率。
分別選擇1,2,3,…,9 s的訓(xùn)練時(shí)間訓(xùn)練網(wǎng)絡(luò),對(duì)應(yīng)每個(gè)訓(xùn)練時(shí)間訓(xùn)練和測(cè)試10次,分別做出每類音樂識(shí)別率和訓(xùn)練時(shí)間的關(guān)系如圖2~圖5所示,兩種神經(jīng)網(wǎng)絡(luò)訓(xùn)練時(shí)間和平均識(shí)別率的關(guān)系如圖6所示。
由圖2可以看出,在重金屬音樂識(shí)別方面,標(biāo)準(zhǔn)算法與改進(jìn)算法相比,開始有較高的識(shí)別率,訓(xùn)練結(jié)束時(shí),標(biāo)準(zhǔn)算法的識(shí)別率高于改進(jìn)算法;由圖3可以看出,標(biāo)準(zhǔn)算法和改進(jìn)算法在山歌音樂方面均有很高的識(shí)別率;由圖4和圖5可以看出,改進(jìn)算法與標(biāo)準(zhǔn)算法相比,具有更高的識(shí)別率。3種算法的對(duì)比如表3所示。
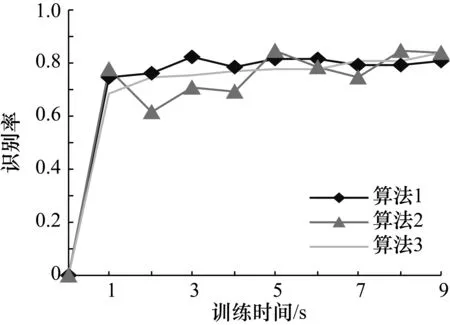
圖2 重金屬音樂識(shí)別率和訓(xùn)練時(shí)間的關(guān)系
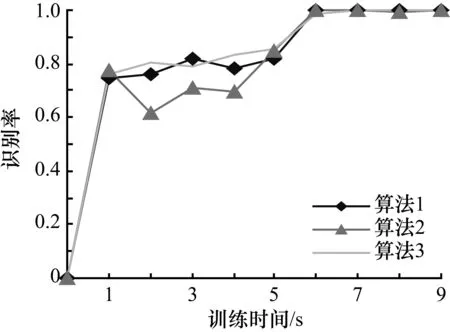
圖3 山歌音樂識(shí)別率和訓(xùn)練時(shí)間的關(guān)系
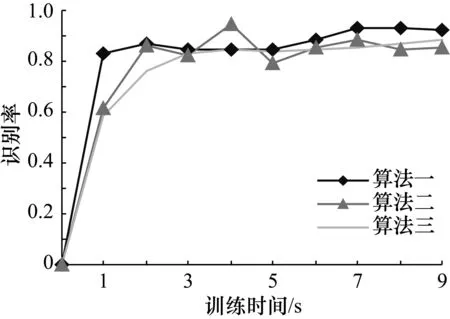
圖4 笛子音樂識(shí)別率和訓(xùn)練時(shí)間的關(guān)系
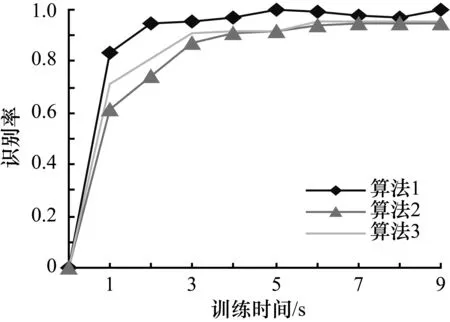
圖5 通俗歌曲音樂識(shí)別率和訓(xùn)練時(shí)間的關(guān)系

圖6 神經(jīng)網(wǎng)絡(luò)訓(xùn)練時(shí)間和平均識(shí)別率的關(guān)系
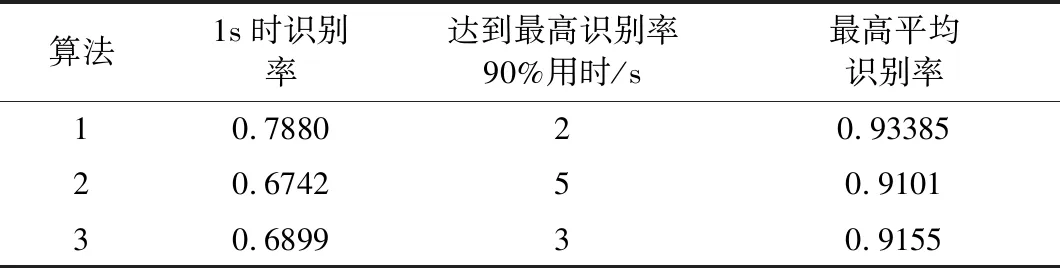
表3 3種算法的對(duì)比
由圖6和表3可以看出,當(dāng)訓(xùn)練時(shí)間在1s時(shí),算法1平均識(shí)別率達(dá)78.8%,其識(shí)別率遠(yuǎn)高于算法2的67.4%和算法3的69.0%,并且在整個(gè)訓(xùn)練過(guò)程中一直保持最高識(shí)別率。最后算法1的識(shí)別率為93.4%,算法2的識(shí)別率為91.0%,算法3的識(shí)別率為91.6%。分別高出算法1識(shí)別率2.6%,算法3識(shí)別率1.9%。在達(dá)到最高識(shí)別率90%用時(shí)方面,算法1為2 s,算法2為5 s,算法3為3 s。算法2節(jié)省時(shí)間60%,算法3節(jié)省時(shí)間33%。而算法3的識(shí)別率在訓(xùn)練過(guò)程中有較大波動(dòng),算法1的波動(dòng)較小。
4 結(jié)束語(yǔ)
本文推導(dǎo)出一種PCA-改進(jìn)RPROP方法的BP算法,通過(guò)對(duì)重金屬音樂、山歌音樂、流行音樂、笛子音樂四種音樂進(jìn)行識(shí)別實(shí)驗(yàn),證明了算法的可行性,同時(shí)可以看出算法在收斂速度,平均識(shí)別率方面均高于標(biāo)準(zhǔn)算法及其部分改進(jìn)算法。但在重金屬音樂的最終識(shí)別率方面,改進(jìn)算法要低于標(biāo)準(zhǔn)算法及其改進(jìn)算法。

