基于GA-GRU環境空氣污染物預測研究

(西南科技大學 信息工程學院，四川 綿陽 621000)

大氣污染形勢嚴峻，以可吸入顆粒物(PM10)、細顆粒物(PM2.5)為特征污染物的區域性大氣環境問題日益突出，嚴重危害著人們的身心健康和生活環境質量。隨著我國工業化、城鎮化的快速推進，資源消耗持續增加，空氣污染防治壓力持續加大。了解空氣質量現狀，及時采取有效措施進行治理，是改善空氣質量的唯一途徑[1]。因此，對環境空氣污染物濃度進行預測成為近幾年的研究熱點。

環境空氣污染物濃度預測分為兩類：機理模型和統計學習模型[1]。其中，機理模型是根據氣象、地理環境和污染源模擬污染物累積、釋放或擴散過程[2]，雖具有很強的適應性、模型參數易調整等優點，但過于依賴精確的數學模型，實現復雜且需要高計算能力的計算機和較長的運行時間[3-4]；統計學習模型不僅善于描述復雜的非線性關系，還避免了對精確數學模型的過分依賴，具有較好的預測精度和運行效率[5-6]。

支持向量機(Support Vector Machine,SVM)、非線性回歸、人工神經網絡(Artificial Neural Network,ANN)和深度信念網(Deep Belief Networks,DBNs)等統計學模型已成功地應用于環境空氣污染物濃度預測研究[7-9]。文獻[7]運用ANN模型預測PM2.5小時濃度，預測系統結構簡單且具有較好地預測能力，但存在局部最優和過擬合問題；文獻[8]在文獻[7]的基礎上利用小波分解和SVM對PM10濃度時序數據進行預測，克服了ANN導致的局部最優和過擬化問題，并且提升了泛化能力，但是數據單一，未做缺失值處理影響預測精度又缺乏數據深度相關性的分析。鄭毅[9]等人基于DBNs方法較好的預測出區域整體的PM2.5日均值變化趨勢，并與RBF的人工神經網絡方法進行比較，得出DBNs方法具有更好的預測精度，但存在局部優化、收斂速率慢和由于采用滑動窗口而導致更早時間之前的序列數據信息丟失問題。文獻[10]運用主成分分析(Principal Component Analysis,PCA)對氣象因子和空氣污染物因子進行降維和提取，并結合最小二乘支持向量機(Least Squares Support Vector Machine,LSSVM)，建立環境污染物PM2.5濃度預測模型，克服了文獻[7]存在的維度災難問題，但局部優化能力和泛化能力弱。上述方法雖都取得較好的預測結果，但仍存在以下幾個問題：① 缺失值未做處理，使時序信息提取不完整；② 維度災難，輸入因子增多，伴隨著訓練樣本大幅度增多，在實際應用中難以滿足；③ 不相關因子的干擾，加入非標識的特征因子，不僅降低模型性能而且干擾模型學習；④ 時間序列內在依賴關系未進行關聯，導致時間序列信息的丟失。基于以上問題和文獻[10]多指標降維思想的啟發，作者考慮到門控循環單元(Gates Recurrent Units,GRU) 神經網絡是在傳統循環神經網絡(recurrent neural network,RNN)上進行改進的，它既能繼承RNN探索序列數據內在依賴關系的能力，又能解決傳統RNN因序列過長而導致的梯度消失、訓練時間長和過擬合等問題，并提升局部優化能力和網絡泛化能力[11]。

因此，本文將綿陽市4個監測站點的環境空氣污染物濃度數據和氣象數據作為數據集，提出將遺傳算法(Genetic Algorithm,GA)[12]和門控循環單元神經網絡相結合的環境空氣污染物PM2.5小時濃度預測模型，以提高空氣污染物濃度預測模型的訓練時間、預測精度和網絡泛化能力等，并通過TensorFlow-GPU深度學習平臺分別與GRU、DBNs兩種預測模型的預測效果進行對比分析，驗證所設計的GA-GRU預測模型的有效性、合理性。

1 研究區域

綿陽，隸屬于四川省，中國唯一的科技城，是重要的國防科研和電子工業生產基地，此外，礦產資源豐富，煤、石油、輕紡工業等發展迅速，因此，PM2.5是綿陽地區中主要的大氣污染物之一[13]。

綿陽市環境空氣污染物的監測采用24 h自動監測的形式，全市共設有4個國控環境空氣污染物監測站點。本實驗數據采用綿陽市2015年1月至2017年12月逐小時環境空氣污染物數據(PM2.5、PM10、SO2、NO2、CO、O3)和每小時更新一次的氣象數據(溫度、溫差、壓強、氣壓、濕度、風速、風向、露點溫度、可見度、降水量)，總數據集共10萬余條。

2 數據預處理

2.1 缺失值算法

在實際數據集中，隨機缺失數據占有相當的比例，數據值缺失是數據分析中經常遇到的問題之一。對缺失值進行填充，能保證信息完整性和結論的準確性。因此，采用線性分段插值與日均值加權和算法進行缺失值填充。

① 缺失標簽。對于一個有缺失值的時間序列xt，其表示第T個時間步對應的時刻(x1=0)，如式(1)所示。

(1)

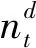
(2)

在原有神經網絡結構的基礎上，結合均值填充和線性插值，設計出本文加權和缺失值處理算法，如式(3)所示。

(3)

2.2 風力編碼

實際監測到的氣象數據，風力大小屬于分類值且具有離散特性，不具備特征之間數據的相關性。因此，在這些數據進入預測模型前，需對數據進行風力編碼處理，即采用One-Hot編碼，通過One-Hot編碼，擴充輸入特征，提高建模的可能性，見表1。

表1 風力編碼表

其中，小于或等于1級風用“0”表示，“1”表示大于一級風。

2.3 數據歸一化處理

為加快預測模型收斂速度，在采用加權和算法對研究數據進行缺失值處理后，結合歸一化算式(4)將研究數據進行歸一化處理。

(4)

在模型預測得到[0,1]之間一個數值后，應用式(5)進行去歸一化，進行模型性能分析評價。

(5)

3 遺傳算法-門控循環單元網絡模型

3.1 GA-GRU預測模型

為減少相關因子的干擾，選擇用GA算法從10個氣象因子和5個主要的空氣污染物濃度中篩選出GRU循環神經網絡模型的輸入因子，實現對GRU循環神經網絡輸入特征的優化與選取，即基于GA-GRU模型的PM2.5濃度預測，其中，GA-GRU預測模型如圖1所示。

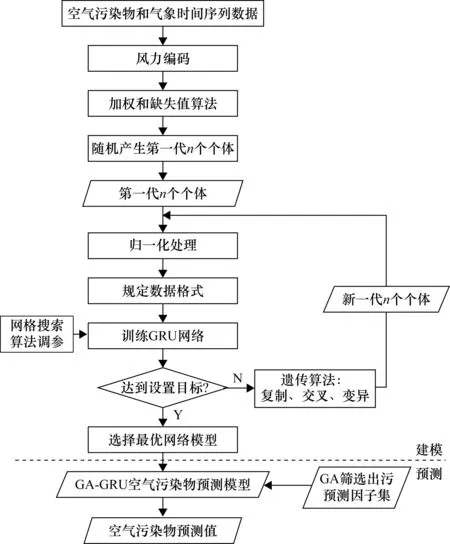
圖1 GA-GRU算法框架

(6)

3.2 GA篩選輸入因子

遺傳算法是一種高效全局搜索可并行化的優化方法，適合大規模問題以及多維多模態問題的求解[14]。面對優化復雜性問題，GA算法可避免精確建模和繁瑣運算，只需運用GA算法的選擇、交叉和變異三種算子便可確定最優解。

首先，定義群體規模每個因子的編碼形式，每個元素分別對應一個因子，取值為“0”或“1”。取“0”為不參與GRU神經網絡的訓練；同理，取“1”即參與。具體步驟如下。

① 在1個臨時群體中，復制n個原群體中的個體。

② 在0～1之間產生一個隨機數，若該隨機數大于預先設定的交叉概率，則隨機選擇2個原群體中的個體，并在隨機確定的若干位置上進行元素交換，并將交換后的向量放入臨時群體中。

③ 若隨機數不大于交叉概率，則隨機選擇原群體中的一個個體，并對其中每個位置隨機產生1個隨機數。反之，對該位置進行變異操作后，將其放入臨時群體中。

④ 重復步驟②和步驟③，直到群體中有n個個體。

⑤ 選出適應度最高的n個臨時群體的個體，組成新一代群體進行遺傳。

⑥ 算法迭代循環，直至滿足設置的目標，遺傳操作結束。

⑦ 選取適應度值最高的l維個體，其中值為1的元素對應的影響因子即為輸入因子集。

下面分別給出選擇算子、交叉算子和變異算子的算法。

① 選擇算子。個體i的選擇概率Ps如下：

(7)

式中，num為群體規模；E(w)為適應度優化目標函數，評價個體優劣，其計算公式為

(8)

② 交叉算子。采用實數編碼種群個體，對配對的粒子i、j進行交叉運算，過程如下。

位置交叉：

(9)

速度交叉：

(10)

式中，α1，α2為交叉概率Pe，取值[0,1]。

③ 變異算子。對第i個個體進行變異運算。

位置變異：

(11)

速度變異：

(12)

(13)

式中，Xmin、Xmax為粒子位置上下界；Vmin、Vmax為變異速度的最小和最大值；g為當前時刻迭代次數；Gmax為最大進化次數；r1、r2、r3為各自的變異概率Pm，取值范圍[0,1]。

3.3 門控循環單元(GRU)

門控循環單元神經網絡是在傳統循環神經網絡上進行改進的，它不僅繼承了傳統循環神經網絡探索序列數據內在依賴關系的能力，又解決了因序列過長而導致的梯度消失、訓練時間長和過擬合等問題[11]。門控循環單元網絡模型如圖2所示。

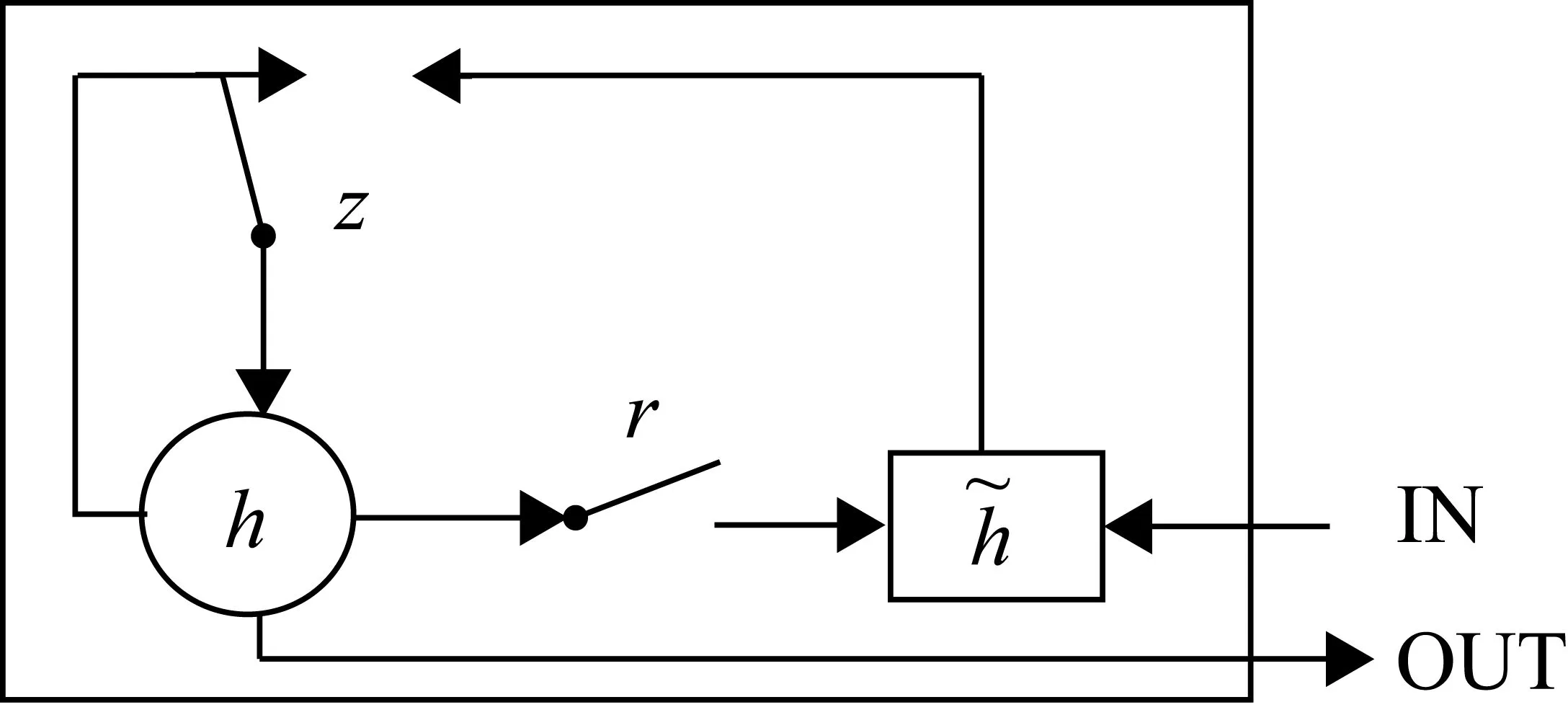
圖2 GRU單元模型

圖2中，⊙為Hadamard乘積；z為重置門；r為更新門。其中，更新門和重置門計算關系式為

zt=g(xtUz+ht-1Wz)

(14)

rt=g(xtUr+ht-1Wr)

(15)

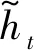
(16)

式中，ht為當前時刻的輸出和傳遞到下一時刻的信息，該過程需要更新門的激活結果zt，計算式為

(17)

其中，zt×ht-1的Hadamard乘積是當前時間步最終輸出結果，也是下一時間步輸入和參與下一時間步的運算。

4 仿真實驗

為了驗證所設計的GA-GRU環境空氣污染物時序預測模型，將綿陽市4個監測站點的氣象數據和環境空氣污染物數據集分為90%的訓練集、5%的測試集和5%的驗證集，通過TensorFlow-GPU深度學習平臺對所設計的GA-GRU模型進行無監督訓練和PM2.5的仿真預測。最后，將GA-GRU預測模型的預測效果分別與GRU、DBNs模型進行對比分析。

4.1 算法性能評價指標

評價模型預測性能優劣，以均方根誤差(Root Mean Squared Error,RMSE)、平均絕對誤差(Mean Absolute Error，MAE)和一致性指數(Index of Agreement,IA)作為評價指標。計算公式如下。

(18)

(19)

(20)

4.2 參數確定

由于存在輸入特征維度災難問題，導致GRU算法計算性能差以及收斂速率過慢。因此，在GRU算法的基礎上，引入GA算法。利用GA算法解決維度災難問題，確定出最優個體。

GA參數：群體規模為num=200，交叉概率Pe=1.0，變異概率Pm=0.050，進化代數為10。根據確定參數，給出GA算法在4個數據集上的最優個體適應度變化曲線，如圖3所示。

由適應度優化目標函數(8)可知，較小適應度值表明神經網絡系統誤差小。因此，結合圖3可知，經過10代進化，4個站點的適應度值已達到最小，確定出輸入向量的最優個體，即2.2節中第7步值為1的元素所組成的輸入向量。

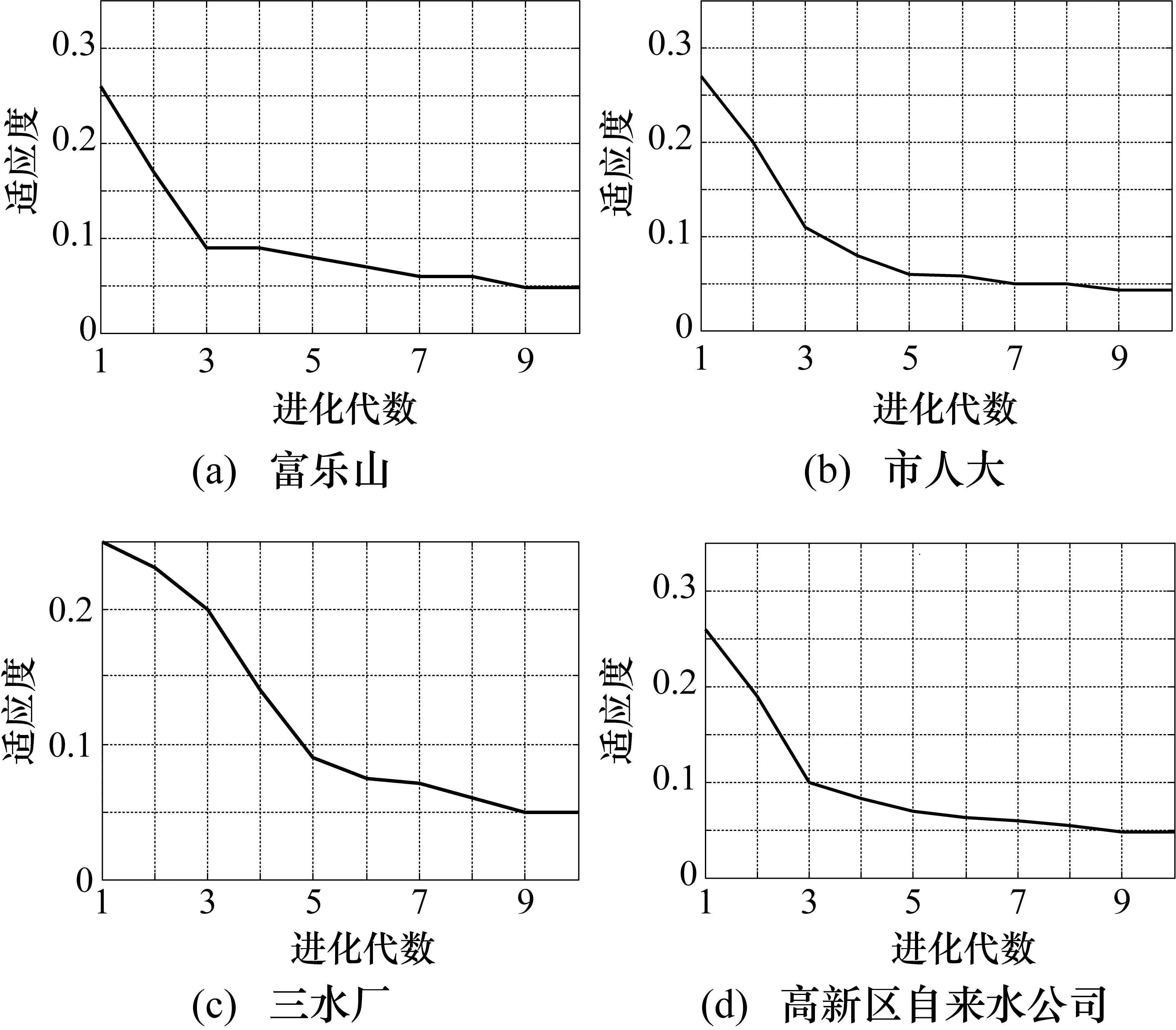
圖3 4個站點最優個體適應度值變化曲線

為解決時序信息丟失問題，采用改進后的循環神經網絡，即門控循環單元神經網絡。通過在4個站點數據集上分別執行網格搜索算法，確定GA-GRU模型的最優深層架構、最優批尺寸(batch_size)、訓練步(epochs)、權值初始化函數(init_mode)以及dropout正則化參數。其中，GA-GRU模型中GRU層數的確定，如圖4所示。

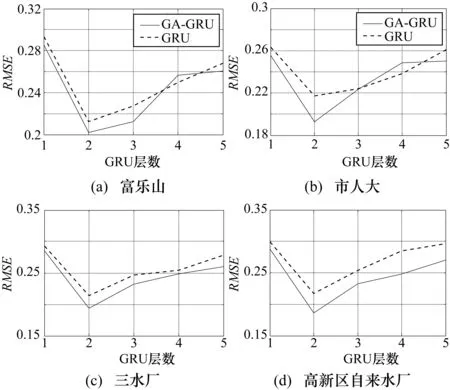
圖4 GRU層數變化曲線

圖4中，縱軸表示模型性能評價指標。由于模型性能評價指標值越低，模型的性能越好。因此，從圖4中可知：當GRU層數為2層時，GA-GRU模型性能最佳。表2給出4個站點的GA-GRU和GRU最優深層架構。

其中，最優深度架構隱藏層包含2層GRU層和1層全連接層，因此，隱藏層并不是越多越好。最后確定的模型參數，如表3所示。

表2 隱藏層層數及神經元數目

表3 模型參數

通過表3確定的最優模型參數，最終分別得到GA-GRU、GRU網絡模型在4個監測站點數據集上的訓練損失與驗證損失圖，如圖5所示。

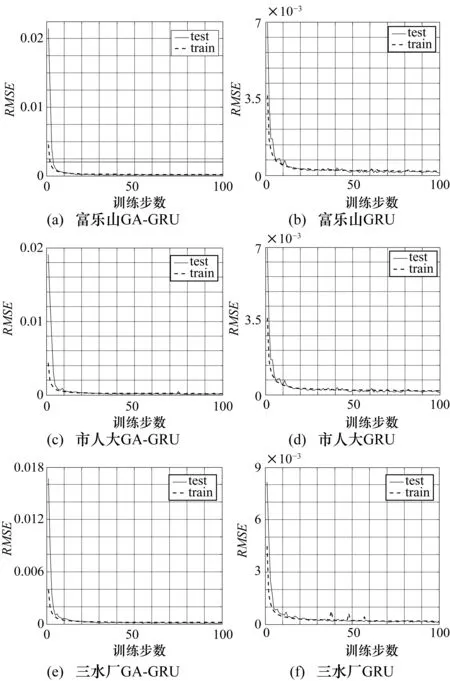
圖5 GA-GRU和GRU模型訓練損失與驗證損失圖

其中，“train”、“test”分別表示訓練集和驗證集上的損失函數；縱軸表示評估預測性能值。結合表3、圖5可知，在4個數據集上都有，當批尺寸為20、訓練步為100、網絡權值初始化參數為glorot_nomal[15]時，GA-GRU模型的處理速度在20個時間步前就開始朝著梯度最小的下降方向收斂，處理速度加快、下降方向準確以及訓練震蕩更小，并且沒有出現過擬合現象。而GRU模型雖然沒有出現過擬合現象，但它從第20個時間步后開始收斂，處理速度稍慢、下降方向存在偏差，并且伴有輕微振蕩。

4.3 仿真結果

為了驗證由4.2節確定的參數，而設計的GA-GRU模型預測精度與性能情況，在綿陽市城區的4個監測站點測試集上，將所設計的GA-GRU模型與GRU模型、DBNs模型進行PM2.5小時濃度預測比較，其仿真圖如圖6所示。

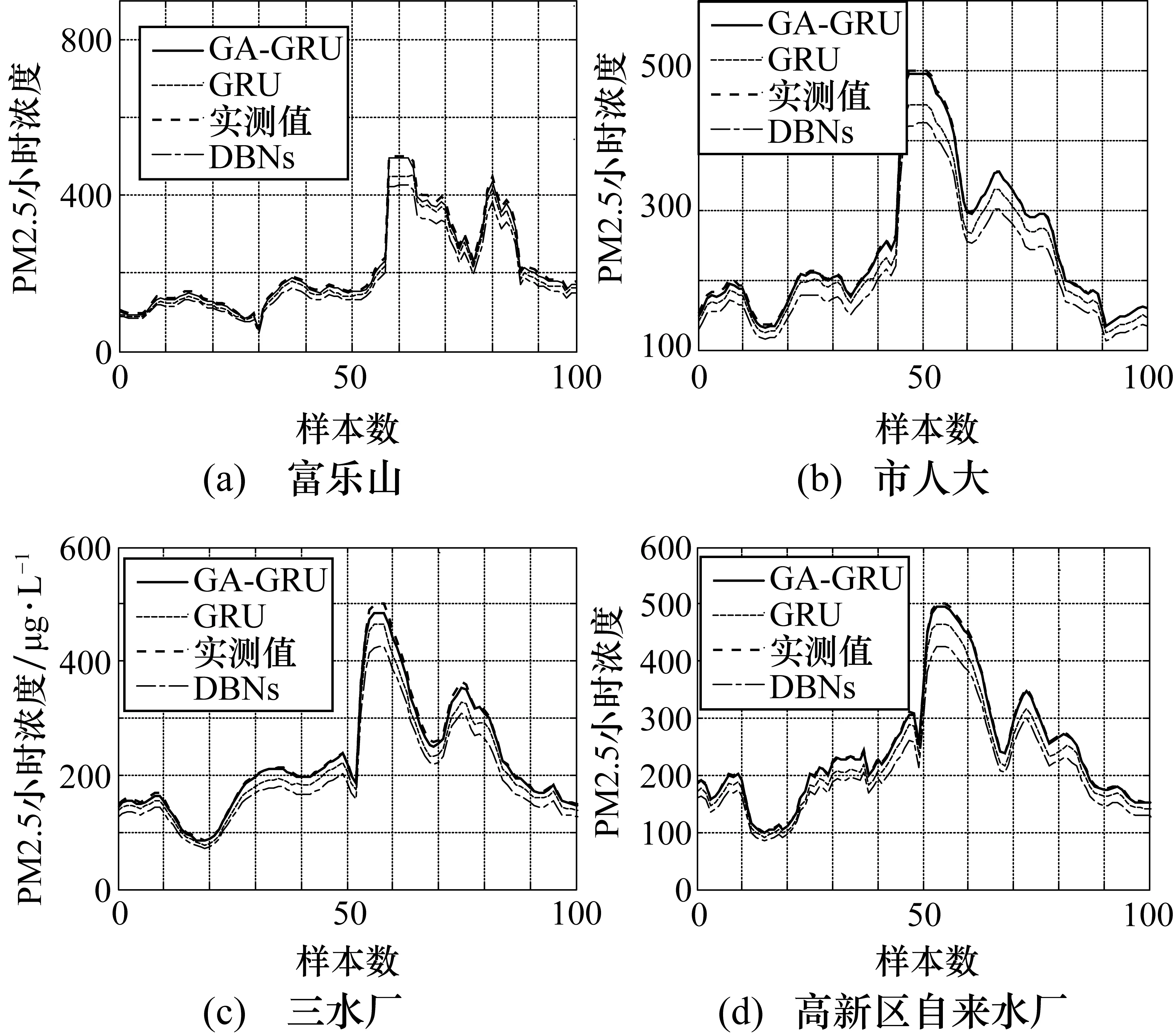
圖6 GA-GRU模型在4個站點預測結果比較

圖6預測結果表明：與GRU模型、DBNs模型相比，所設計的GA-GRU模型具有高擬合程度和高預測精度，已達到項目所要求的95%。而GRU精度為92%，深度信念網絡的精度為88%左右。在富樂山數據集上，當PM2.5小時濃度值達到最大值500 μg/L時，GA-GRU模型預測值達到495 μg/L，而GRU、DBNs分別為450 μg/L和420 μg/L；在市人大數據集上，當PM2.5小時濃度值達到最大值500 μg/L時，GA-GRU模型預測值達到493 μg/L，而GRU、DBNs分別為453 μg/L和425 μg/L；在三水廠數據集上，當PM2.5小時濃度值達到最大值500 μg/L時，GA-GRU模型預測值達到495 μg/L，而GRU、DBNs分別為448 μg/L和425 μg/L；在高新區自來水公司數據集上，當PM2.5小時濃度值達到最大值500 μg/L時，GA-GRU模型預測值達到491 μg/L，而GRU、DBNs分別為447 μg/L和423 μg/L。綜上所述，當PM2.5值較大時相較于GRU、DBNs模型，GA-GRU模型能更好獲得滿意的預測結果。

最后，為了更加全面評價所設計的GA-GRU模型性能,下面列出評價模型性能的3個統計值MAE、RMSE、IA及模型訓練時間，如表4所示。

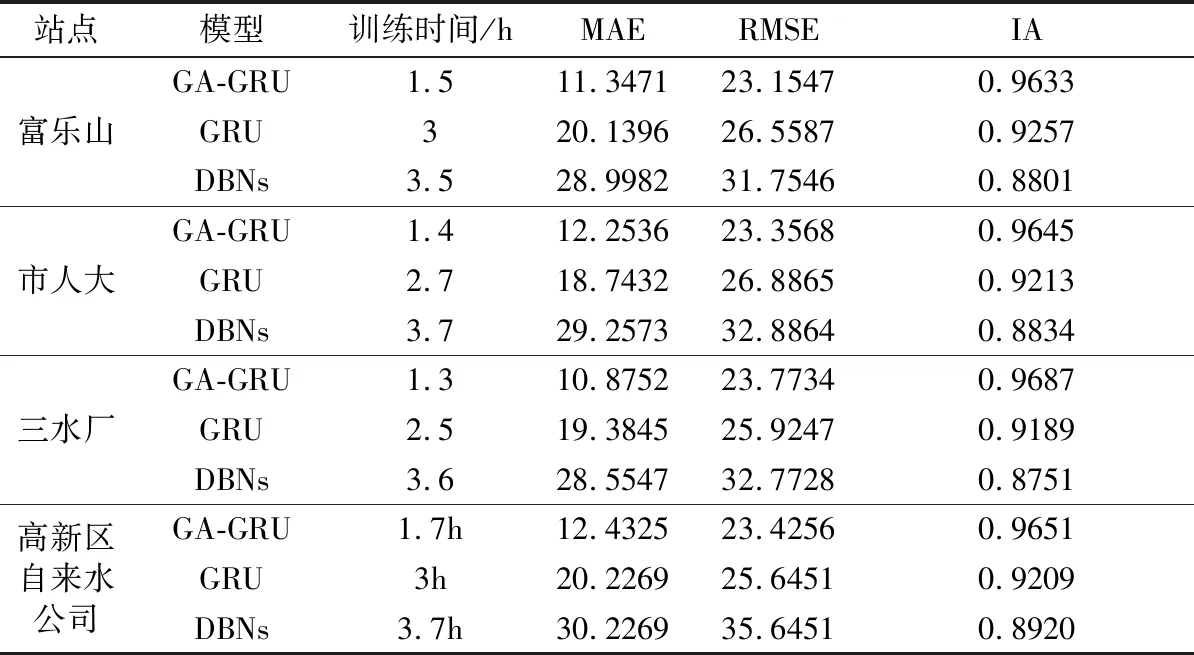
表4 模型預測性能比較結果

從表4可知，與GRU模型、DBNs模型相比，所設計的GA-GRU模型在均方根誤差、平均絕對誤差和一致性指數這3種性能評價指標中有較好改進。其中，一致性指數(IA)提升尤為明顯，表示GA-GRU模型具有更準確的時序預測能力；而平均絕對誤差(MAE)、均方根誤差(RMSE)較小，表明GA-GRU模型預測精度較高，泛化能力較好，能更加有效地預測PM2.5濃度變化趨勢，對空氣污染物控制具有有效的指導作用。值得注意的是，從表4訓練時間一列可得，GA-GRU訓練時間相較于GRU、DBNs模型分別提升了50%、57%左右。因此，GA-GRU模型訓練時間上有較大的提升，表明前期GA處理輸入特征取得良好的效果。綜上所述，所提出的GA-GRU預測模型能有效預測PM2.5小時濃度，并且具有較強的魯棒性。

5 結束語

所設計的GA-GRU預測模型在環境空氣污染物PM2.5小時濃度預測中，對大樣本數據集，該模型不僅保留了處理數據維度和輸入特征的能力，并且在一定程度上充分挖掘了環境空氣污染物因子自身之間與氣象因子之間潛在的特征關系。仿真實驗結果表明，相較于門控循環單元神經網絡模型和深度信念網絡模型，GA-GRU預測模型在訓練時間、擬合度、泛化能力和預測精度上都有所提升且具有更強的魯棒性。在未來研究中，將考慮加入影響環境空氣質量的其他因素，例如，季節因素、地域因素和車流量等，為相關部門進行空氣環境污染防治提供理論支撐與決策依據。