基于SVM決策樹的自適應相數ECT圖像重建算法
(上海海洋大學 信息學院,上海 201306)
多相流辨識廣泛應用于石油、動力、能源等各種領域中。在自然界及工業檢測過程中,因為多相流流動特征復雜、隨機性較大,現今的數學模型都很難對其進行完整描述,而測量的精確度也不高[1]。隨著計算機技術的快速發展,電容層析成像技術(Electrical Capacitance Tomography,ECT)在多相流流動的在線檢測方面發展迅速[2]。該技術具有測量速度快、非侵入、成本低、適用范圍廣等特點[3]。但是迄今為止,多相流的在線檢測成像技術只有少數已商品化,且多適用于兩相流。而ECT技術應用于在線測量與控制的過程中,經常因為被測管道中的相數未知而無法實現相數自適應的分類算法,導致無法處理多種不同物質混雜的多相流問題的情況。
目前針對以上問題,有研究者提出用遺傳算法作為學習算法的RBF神經網絡可以用于ECT圖像重建[4-6],也有研究者提出用基于支持向量機(Support Vector Machine,SVM)的ECT圖像重建算法來解決此類問題[7],將ECT的圖像重建問題歸結為非線性軟間隔問題,利用SVM四層網絡的泛化性解決多相流問題。但這些方法都沒有從多相流相數自適應的角度來解決圖像重建問題。
本文主要利用SVM與決策樹相結合的SVM決策樹方法在分類速度和分類精度上的優勢,對電容層析成像圖像重建進行研究,結果顯示,該算法能適應多相流相數變化,即面對多相流,該算法有較高的圖像重建速度和精度。
1 基于SVM決策樹的自適應相數預測模型的重建算法
1.1 決策樹
在多分類問題中,會存在具有相同特征的樣本聚集在一個集合中的情況,而這些集合便是“類簇”,針對多相流進行相數預測時,不同相數的樣本會對應不同的類簇[8-9]。本文提出的預測模型就是圍繞類簇開展的,SVM決策樹(Decision Tree SVM,DTSVM)[10-13]的原理是:在對不同相數的樣本進行分類時,把所有樣本歸為兩類,通過決策函數進行計算,歸類計算所得的值,根據值的正負形成兩個子類,繼續循環,直到把所有類別都歸類到其所對應的類簇,而SVM決策樹是通過支持向量機進行決策分類。圖1是針對樣本數為4時,所采用的幾種不同SVM決策樹層次構型。圖1(a)是當對樣本無先驗知識時采用的構型;圖1(b)是當對樣本有充分先驗知識時采用的構型,其思路是首先構造一棵最優的SVM決策樹,然后再在子類的基礎上繼續分類;圖1(c)是當對樣本有部分先驗知識時采用的構型。因為本文對樣本無先驗知識,所以在對相數進行判斷時,選擇層次構型1(圖1(a))對相數進行分類。
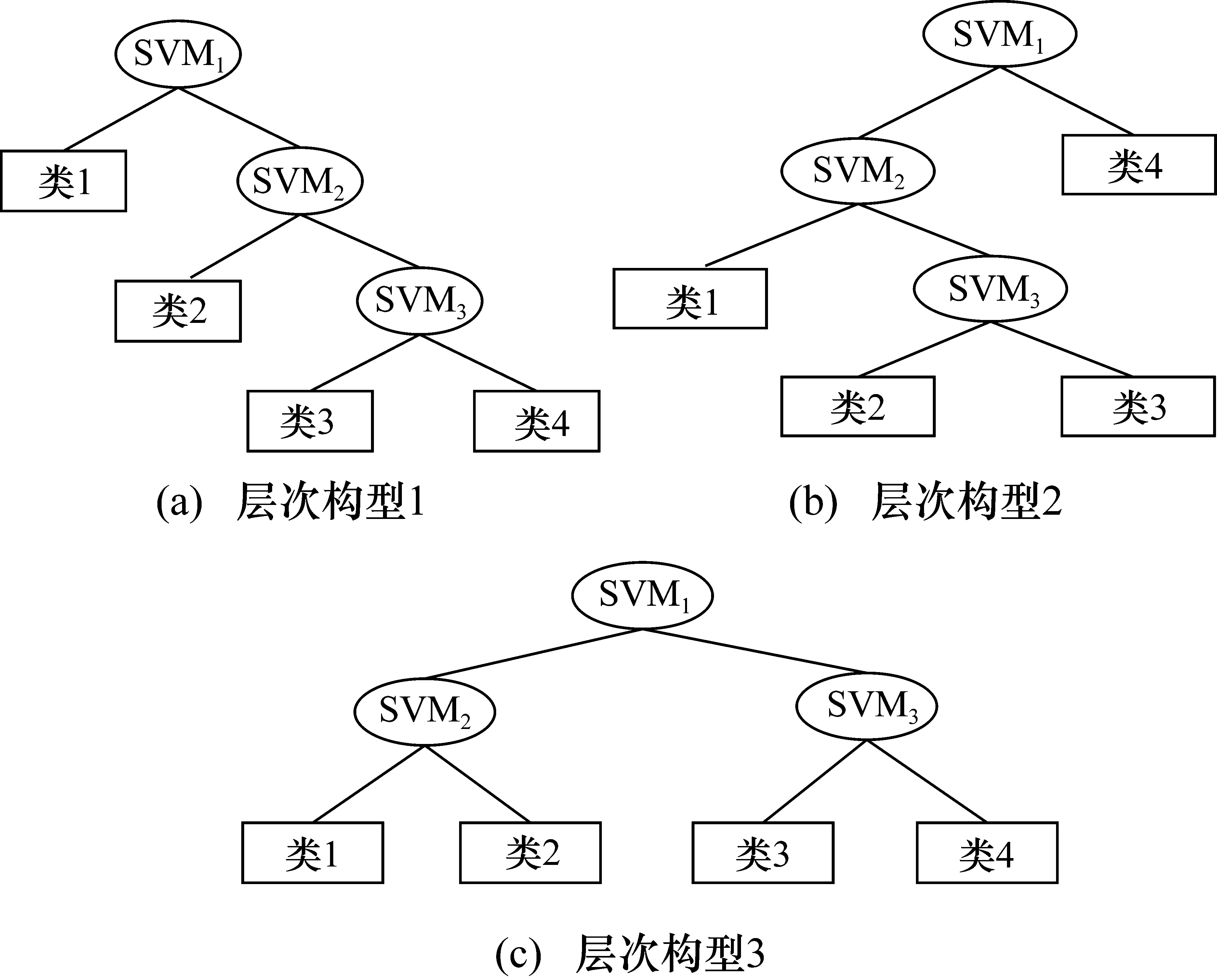
圖1 4類問題對應的SVM決策樹層次構型
對于N類樣本的分類問題,一對一的支持向量機多分類方法在訓練時分別需要構建N(N-1)/2個支持向量機分類器,而一對多的支持向量機多分類方法在訓練時分別需要構建N個支持向量機分類器,而本文所采用的方法只需構建N-1個支持向量機分類器。因此可以看出本文采用的分類器在分類效率上明顯優于后兩種。
1.2 基于SVM決策樹的自適應相數預測模型

利用SVM決策樹實現自適應相數預測的具體實驗步驟如下:
① 訓練集的選取。把A1~A2M-1種不同介質形成的分布所對應的電容值提取出來,作為實驗的訓練集Train。
② 單相樣本的預測。建立SVM分類器,分離單相樣本類和其他相數的樣本類,找出所有具有單相的樣本,單獨對單相的樣本進行預測。
③M相樣本的預測。建立SVM分類器,分離M相的樣本類和其他相數樣本類,找出所有具有M相的樣本,單獨對M相的樣本進行預測。
④K相樣本的預測。建立SVM分類器,分離K相的樣本和其他相數的樣本類,找出所有具有K相的樣本,單獨對K相樣本進行預測;重復此步驟。
圖2為三相流對應的基于SVM決策樹的自適應相數預測模型,其中A1~A3是單相流,A4~A6是兩相流,A7是三相流。從圖中可看出,SVM1實現A1~A3與A4~A7的分類,SVM2實現A1與A2、A3分類,SVM4實現A2與A3分類,SVM3實現A7與A4~A6分類,SVM5實現A4與A5、A6分類,SVM6實現A5與A6分類,此模型實現了每種相數的自適應。
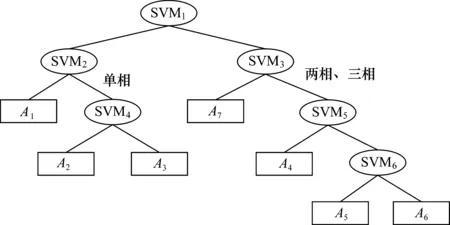
圖2 三相流對應的基于SVM決策樹的自適應相數預測模型
2 仿真實驗
2.1 基于SVM決策樹的自適應相數預測模型建立
將氣/油兩種物質作為研究對象,對應的介電常數分別為εg=1和εo=2.2。將管道內其他介質的介電常數設為εi,而管道內樣本的相數會出現以下情況:單相流,單一介質為εg、εo、εi;兩相流,任意兩種介質的組合εg和εo、εg和εi、εi和εo;三相流,3種介質的組合εg、εo和εi。
實驗中,對8極板ECT系統進行實驗仿真,進行數據采集。設管道壁的介電常數為2.5,對管道使用有限元剖分法,將其截面剖分為192個單元,并對極板電容進行計算。
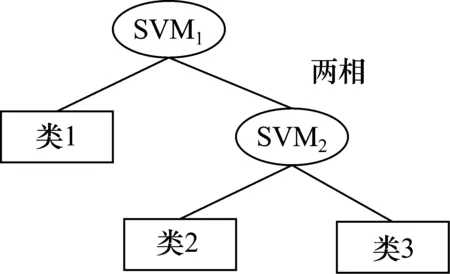
圖3 管道相數分類模型中SVM決策樹層次構型
本實驗采用8極板ECT系統,極板間有28個獨立測量的電容值,將這28組電容值作為特征數據,從中提取1356組數據作為測試樣本,提取5612組數據作為訓練樣本,使用圖3中的層次構型分類管道中存在的樣本。如圖4、圖5所示,樣本的介電常數εi∈[2.3,5.3],實驗驗證了SVM決策樹多分類方法進行相數分類預測的可行性,其次與普遍使用的One-Versus-Rest(OVR)分類算法分析比較,在此區間中 SVM決策樹多分類預測精度更加理想。
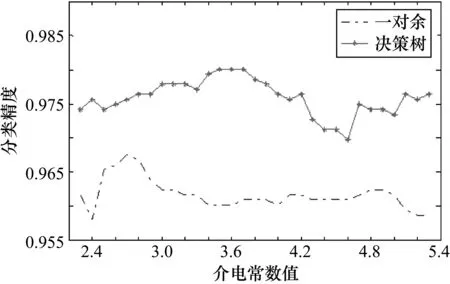
圖4 測試集整體精度
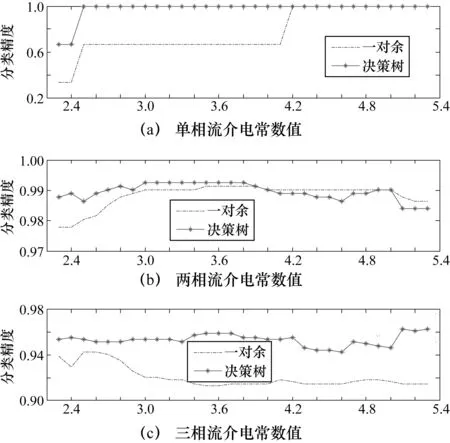
圖5 不同類別測試集精度
由圖4可知,在區間εi∈[2.3,5.3]范圍內,對測試集整體精度的預測絕大部分超過97%。由圖5可知,在εi>2.4的區間上,對每一種類別的測試集的預測精度也都超過95%。由實驗可知,SVM決策樹算法分類精度更高,而且性能穩定,在分類效果和泛化能力上也更具有優勢。
為了檢驗SVM決策樹相數分類預測模型在各種物質并存的情況下依然可以適用,如表1所示,選取氣、油、水(εg=1,εo=2.2和εw=80)作為實驗對象進行分類預測,SVM決策樹分類算法的測試集整體分類精度在97.42%左右,且基于SVM決策樹算法在不同相的分類精度比較中都高于OVR算法。如表1所示,運行時間單位為s,SVM決策樹算法的分類速度也快于OVR算法。從表中可知,SVM決策樹算法不僅在分類精度上更優,而且在分類速度上相較于OVR算法也有顯著的提升。
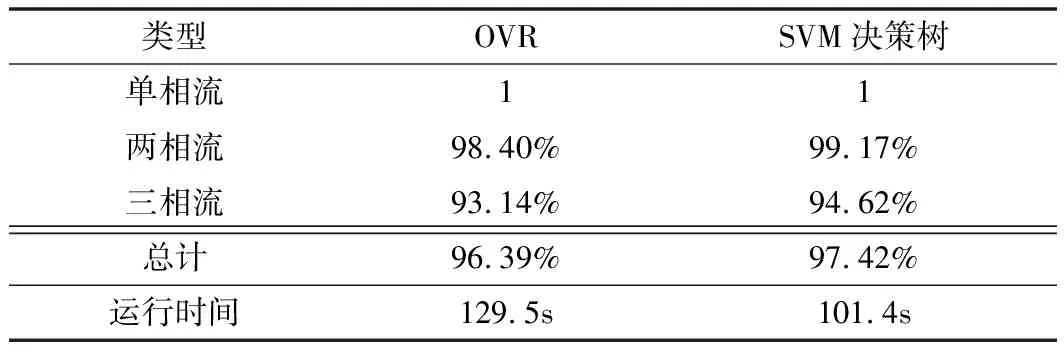
表1 管道中相數分類精度結果
以上實驗是通過分類不同的相數來分類管內的不同狀態。本文在以上實驗成果之上,繼續分析了基于SVM決策樹的自適應相數預測模型,對優化管內相數的自適應能力做了進一步的探討。如果管道中存在三相,那么最多會出現A1~A7這7種可能。
單相流:A1:εg=1,A2:εo=2.2,A3:εw=80;
兩相流:A4:εg=1,εo=2.2,A5:εg=1,εw=80,A6:εo=2.2,εw=80;
三相流:A7:εg=1,εo=2.2,εw=80。
表2為管道中自適應相數模型的分類精度結果。

表2 管道中自適應相數模型的分類精度結果
根據表2可知,當出現7種介質共存的情況時,基于SVM決策樹的自適應相數預測模型可以實現各相數之間的分類,SVM決策樹算法的泛化能力優異,可以更好地解決相數自適應問題。
2.2 基于SVM決策樹的自適應相數的ECT圖像重建
本文建立基于SVM決策樹的自適應相數ECT圖像重建算法的體系結構,更為直觀地分析SVM決策樹的自適應相數ECT圖像重建算法,并對其進行性能優化,如圖6所示。把經過相數自適應的各類樣本分別進行歸一化和圖像重建。
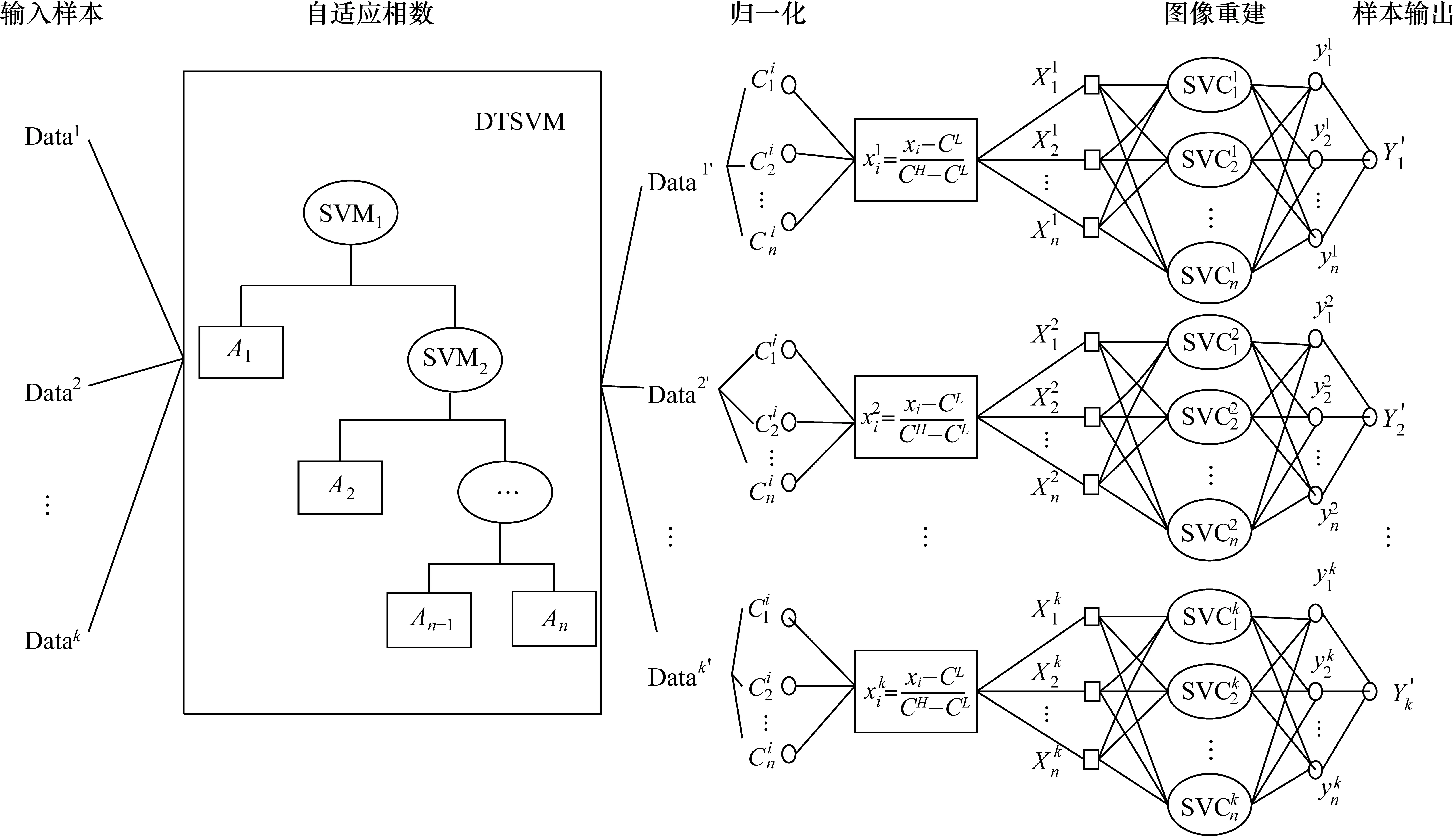
圖6 基于SVM決策樹自適應相數ECT圖像重建算法的體系結構
實驗步驟如下。
(1) 訓練集和測試集采集:選取訓練集Train和測試集Test。
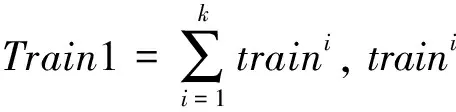
(2) 預處理數據。
在相數已經得到確認的情況下,分別使用并聯歸一化模型對樣本進行歸一化處理,得到自適應相數的電容歸一化模型,獲得了數據預處理后的訓練集Train′和測試集Test′。
(3) 數據成像。
多相流圖像的重建是多分類問題,把不同介質的灰度作為樣本的標簽,進行訓練建模。設數據預處理后的訓練集為Train′,選適當的核函數和適當的參數C,構造并求解最優化問題。
(1)
(2)
0≤αi≤Ci=1,…,N
(3)
得最優解為
構造決策函數為
圖7是分別利用兩種多相流自適應算法下典型流型的重建得到的圖像,第一欄圖像為仿真實驗的原始圖像,第二欄圖像為使用OVR算法進行圖像重建所得圖像,第三欄為使用SVM決策樹自適應算法后圖像重建所得圖像。從重建圖像可以看出:基于SVM決策樹自適應相數的重建圖像效果優于OVR算法,具有較高的準確度,整體的重建精度得到了提升。
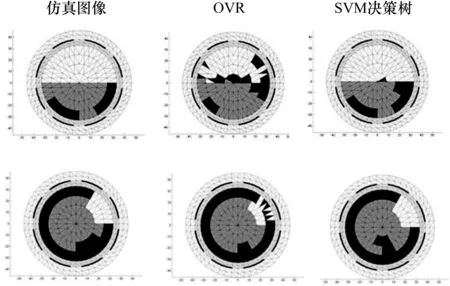
圖7 兩種多相流自適應方法的重建圖像
3 結束語
電容層析成像系統已經廣泛應用于多相流檢測領域中,本文通過改進SVM實現自適應相數ECT圖像重建算法,基于SVM決策樹的相數自適應模型可以很好地應對實際應用中存在的需求。為了驗證算法的性能,通過基于SVM決策樹的自適應相數預測模型進行實驗。該預測模型可以以較高的精度來區分管內包含的介電常數差異不大的介質,且重建圖像的精度較高。該算法是解決相數不確定的多相流問題的一個有效途徑。

