多普勒信號的Burg算法優化研究
(1.北京交通大學 機械與電子控制工程學院,北京 100044; 2.北京宇航系統工程研究所,北京 100076;3.中國北方工業有限公司,北京 100053)
高速列車測速大多采用多普勒測速方式,其安裝在列車底部避免了傳統接觸式列車測速方式由于列車運行時速過高帶來的軸承磨損、空轉等誤差[1-2]。在列車測速過程中由于運行環境復雜,如路面變化、周邊列車影響,多普勒測速反射回波是由多個回波信號疊加而成的。一般將回波信號看作平穩隨機信號,通過譜估計法對多普勒信號進行頻域信號分析。譜估計分為經典譜估計與現代譜估計兩種,以AR參數模型法為代表的現代譜估計對觀測數據進行外推,預測求出觀測數據以外的其他數據,極大增大了頻譜的分辨率。在實際列車測速中,需要根據信號的有限采樣點來估計AR模型參數。常用方法有Yule-Walker法、協方差法、Burg算法和改進協方差法[3-4]。其中改進協方差法為Burg算法的進一步發展。針對Burg算法的誤差來源,分析了基于窗函數的優化算法,并針對改進的協方差法實現了基于預測誤差功率最小意義的優化算法。仿真實驗證明,優化算法對多普勒信號功率譜估計能力均有很大改善。
1 Burg原理及誤差分析
1.1 Burg原理
Burg 算法基于線性預測器的前、后向預測的總均方誤差之和最小的準則直接從觀測數據來估計反射系數,然后通過Lenvinson-Durbin算法的遞推公式求出AR 模型參數[5]。這種算法對未知數據不需要做任何假設,估計精度較高。方法如下,前、后向預測誤差平均功率為
(1)

(2)
式中,km為反射系數即模型k階模型的第k個系數;m為模型階數,m=1,2,…,p。然后利用L-D遞推公式遞推出模型參數:
(3)
式中,k=1,2,…,m-1。
am(m)=km
(4)

(5)
1.2 誤差分析
在Burg算法推導原理中可以看出。在L-D遞推公式中,高階系數由一階系數遞推。因此一階參數估計誤差對高階參數有一定影響。為分析一階參數影響,給定信號x(n)=sin(ωn+θ),初相位為θ,歸一化頻率為ω。由Yule-Walker方程[6]可得一階模型參數a1(1)的真實值為a1(1)=-cosω。將信號公式代入反射系數km公式(式(2))中,求得a1(1)估計值為
(6)
式中,第二項為一階模型參數估計誤差,可以算出當初相位θ為π/4的奇數倍;信號長度N為1/4周期的奇數倍時誤差最大[7]。
2 兩種Burg優化算法
2.1 基于窗函數的優化算法
由式(3)~式(5)可知,模型參數直接由反射系數求出。為減小誤差可直接對反射系數km進行修正。引人補償系數ωn(m),其相當于對信號進行加窗處理,進一步提高其方差能力,從而降低頻譜偏移程度、改善頻譜分辨率。Kaveh M等人基于平均頻率誤差方差最小原則得出最優窗函數為[8]
(7)

(8)
2.2 基于預測誤差功率最小意義的優化算法
由誤差分析可知,高階參數由低階參數遞推得到。低階參數誤差對高階參數推導有一定影響,導致譜估計質量下降。針對改進的協方差法原理中?ρm/?a(m,i)=0對原算法做如下改進[10-11]:在預測誤差功率最小的意義下直接求解高階模型系數,為保證不增加過多計算量,可先求二階預測誤差功率。由先計算一階模型參數a1(1),改為先計算二階參數a2(1)、a2(2)。如式(9)所示,先求二階誤差平均功率:

(9)
接下來計算二階模型系數a2(1)、a2(2)。
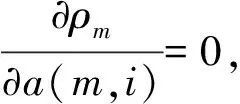
(10)
式中,各參數如下:
(11)

(12)
由式(12)可以看出,改進算法通過二階參數的推導間接修正了一階參數估計誤差,避免了誤差項的影響,因此譜估計精度有了極大提高。
3 仿真分析與實驗驗證
3.1 算法性能對比
輸入仿真信號為
x(t)=sin(2π·50·t+π/4)+0.5randn(size(n))
(13)
給定信號頻率為50 Hz,初相位為π/4,采樣點數N為55,其相當于1/4信號周期的11倍。由1.2節誤差分析可知,此時的數據長度和初相位為最不利情況。信號混有均值為0,方差為1的隨機噪聲干擾。
取采樣頻率為1 kHz,模型階數m=7。對原Burg算法及兩種優化算法進行功率譜估計對比,結果如圖1所示。從圖1中可以看出,原算法頻譜分辨率最差與給定信號可達到5.66 Hz偏差,兩種優化算法的頻譜分辨率均有一定改善,可有效抑制頻譜偏移。其中基于預測誤差功率最小意義的Burg優化算法2的譜估計能力最好,與原信號只有0.29 Hz的頻率偏差。

圖1 不同算法的譜估計性能對比
3.2 算法復雜度分析
對原算法及兩種優化算法進行復雜度分析,當模型階數m=7時,結果如表1所示。

表1 算法復雜度分析表
從表1中可以看出,優化算法1中運算次數較多,而優化算法2只增加了2m-13次乘法,m-6次加法,對算法復雜度影響不大。3種算法運行時間大致相同,說明優化算法在不增加運行時間的前提下提高了頻譜的估計能力,對原算法起到了明顯優化作用。
3.3 模型參數對算法性能影響
給定信號:
x(t)=5sin(2π·300·t)+3sin(2π·305·t)+0.5randn(size(n))
(14)
信號包含300 Hz和305 Hz頻率分量。為滿足采樣定理,取采樣頻率為1000 Hz。首先固定FFT點數為1024,給定不同采樣點數N。
由圖2中看出,隨著采樣點數N的增加,頻譜分辨率越來越好。但由于采樣點數增加會造成計算量的增大,不能滿足列車測速的實時性要求。綜合考慮頻譜計算精度與實時性要求,取采樣點數N為1024點。FFT計算點數參數選擇過程同理,取FFT點數為1024點。

圖2 不同采樣點數N對算法性能影響
3.4 列車測速范圍內算法的譜估計驗證
列車速度與多普勒頻率的計算公式為[8]
(15)
式中,v為列車速度(km/h);fd為多普勒頻率;f0為雷達發射波頻率,為24.125 GHz;σ為雷達發射波方向與地面的夾角,假設為0°;c為光速3×108m/s。
由于高速列車被測速度范圍為0.2~600 km/h,由式(15)可知,多普勒頻率fd的范圍在8 Hz~27 kHz之間。
為驗證優化算法在列車測速過程中的適用性能,分別給定待測量頻率范圍內不同頻段信號頻率組,三組分別為51 Hz、306 Hz、2006 Hz;4050 Hz、9000 Hz、14 kHz;22.2 kHz、24.9 kHz、26.3 kHz。綜合考慮頻率分辨率與系統實時性處理要求,對第一組頻率分量采用8 kHz采樣頻率,后兩組采用80 kHz采樣頻率。使用Matlab對算法譜估計能力進行仿真,結果如圖3所示,圖中可以看出優化算法在各個頻段內適應性良好,可準確估計出各個頻段的信號頻率。

圖3 測速范圍內不同頻段Burg算法譜估計
3.5 基于實測數據的的譜估計驗證
為進一步驗證算法實用性,實物如圖4所示,通過信號發生器給定上述三組頻率,通過DSP進行信號處理測試算法譜估計能力。測試結果如表2所示,表中可以看出,算法可以準確識別各個頻段頻率且誤差小于1%。

圖4 DSP信號處理實物圖

理論頻率/Hz實測頻率/Hz理論速度/km·h-1實測速度/km·h-1頻率誤差/%5150.78 1.14 1.13 0.43 306308.59 6.90 6.84 0.85 20062007.81 44.91 44.87 0.09 40504062.50 90.86 90.58 0.31 90008984.38 200.95 201.30 0.17 1400013984.38 312.78 313.13 0.112220022187.50 496.25 496.53 0.062490024921.88 557.41 556.92 0.092630026328.13 588.86 588.24 0.11
4 結束語
針對多普勒信號處理的Burg算法進行了研究,分析其推導原理及產生誤差原因。對于模型低階參數估計誤差來源進行了兩種修正優化算法分析。一種是基于窗函數的優化,另一種基于預測誤差功率最小意義的優化。通過Matlab仿真分析對比了原算法與兩優化算法的功率譜估計能力,選擇出模型最優參數,并對列車測速范圍內進行了優化算法的譜估計驗證。實驗結果表明,兩種優化算法在不增加運行時間的基礎上對頻譜估計性能均有極大改善,可以識別出列車測速范圍內各個頻段頻率,譜估計頻率誤差小于1%。

