基于DPSO-AO*算法系統測試序列優化問題研究

王麗麗, 林 海2, 包 亮3, 萬 賀

(1.北京交通大學 機械與電子控制工程學院，北京 100044；2.北京宇航系統工程研究所，北京 100076； 3.北京航天自動控制研究所，北京 100854)

科技發展所帶來的電子系統的結構和功能越來越復雜，特別是在航空航天和軍事等重要領域，對電子系統的測試效率和正確率要求非常嚴格。但是，普遍存在的測試手段是通過測試人員(受過專業培訓)在經驗的基礎上分析、診斷；因測試人員的不同造成測試結果的不穩定性很高，并且受人本身能力的限制，測試效率也不高。為解決以上問題，系統首先需要解決測試序列優化的問題，目前國內外已經提出了一系列相關技術，主要分為三類，分別為：基于圖論的方法、基于搜索的方法和其他方法[1]。針對實現測試策略生成的問題，目前已經有很多種方法,包括遺傳算法、差分進化、量子遺傳算法、BP神經網絡、模擬退火算法，以及對于這些算法的融合算法[2-4]。

由于AO*算法在研究測試序列問題上應用的比較多,但是AO*算法在搜索最優路徑的過程中需要對每個測試進行擴展，這對于復雜的信息系統而言，計算量太大[5-6]。為了改進該算法，采用離散粒子群算法，對每次需要擴展的測試集進行優化選擇，然后AO*算法只對優化的結果進行擴展，這樣的處理使得整個過程的計算量大大減少，搜尋最優路徑的時間也大大縮短。

1 測試序列優化問題的數學模型

1.1 系統的多信號流圖模型和相關矩陣

建立了復雜裝備信息處理系統，在此基礎之上，計算了該系統的故障測試相關矩陣，然后基于系統的相關矩陣進行測試優化選擇問題研究[7]。建立的復雜裝備信息處理系統的多信號流圖模型如圖1所示。

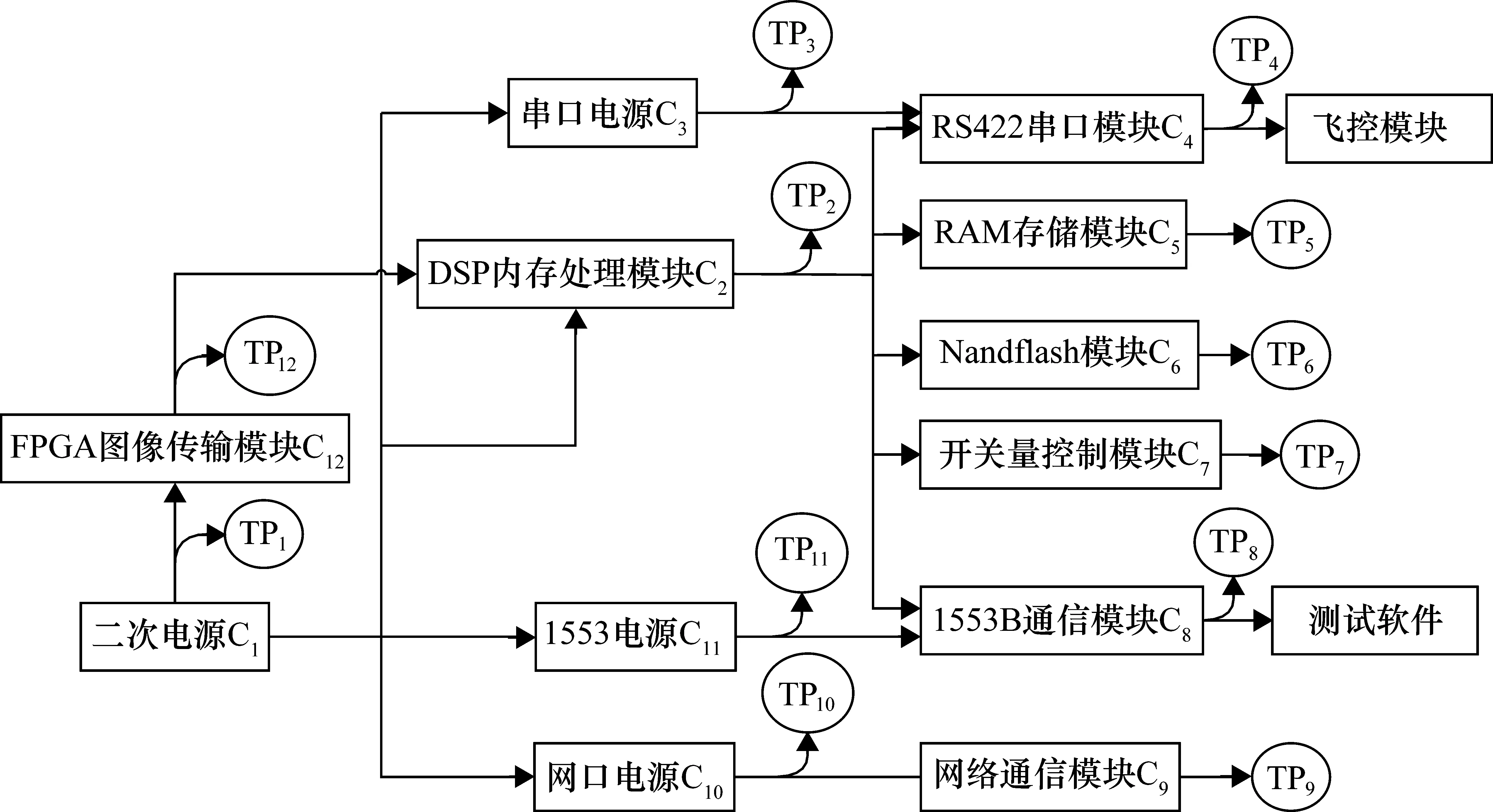
圖1 復雜裝備信息處理系統多信號流圖模型

如圖2給出了計算系統相關矩陣的方法，得到系統的故障-測試相關矩陣如表1所示。

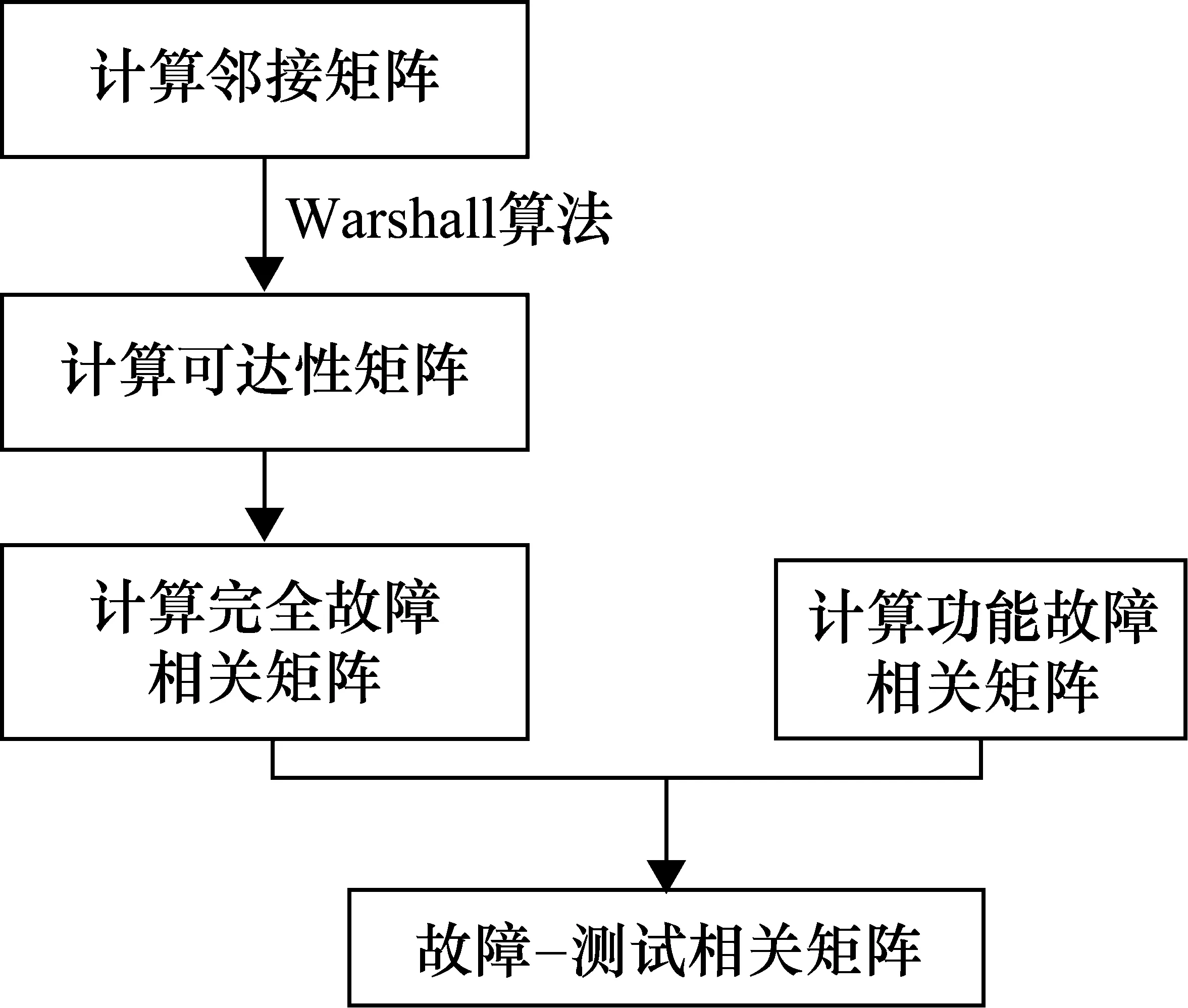
圖2 系統相關矩陣的計算流程圖

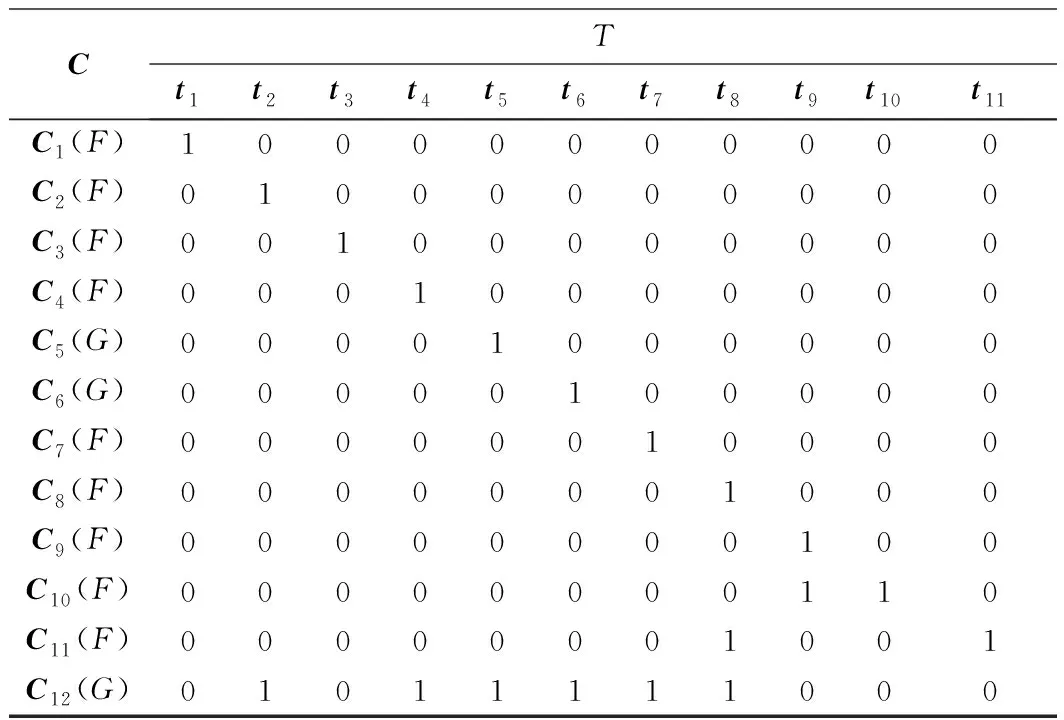
CTt1t2t3t4t5t6t7t8t9t10t11C1(F)10000000000C2(F)01000000000C3(F)00100000000C4(F)00010000000C5(G)00001000000C6(G)00000100000C7(F)00000010000C8(F)00000001000C9(F)00000000100C10(F)00000000110C11(F)00000001001C12(G)01011111000

表1中行向量表示信息處流系統中可能發生的故障，C(F)表示功能故障模式，C(G)表示完全故障模式；列向量分別表示針對系統的故障源設計的測試。本文的目的就是對這些測試項進行優化選擇，期望在系統發生故障時，以最少的測試項對系統故障進行檢測和隔離，使產生的測試代價最小。

1.2 數學描述

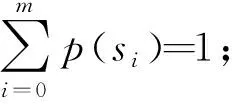
p=[999640,28,7,31,27,8,9,127,31,26,29,27,10]T×10-6

四元組參數中T={t1,t2,…，tn}是n個可用測試組成的集合，已知n=11。c=[c1,c2,…,cn]T表示測試費用的向量[8]。

1.3 與或樹搜索算法及解樹的代價

與或樹能將搜索路徑清晰地展示出來，構造與或樹的過程就相當于將問題一步一步分解，直到分解成不能再分解的子問題。這種方式會搜索所有的路徑然后去判斷每個路徑的好壞，所以對于復雜的信息處理系統而言，這種方法代價會很高，不適合采取[9]。

本文將利用AO*算法，由于該系統相關的系統參數引導，使進行的每一步搜索均為最佳路徑，避免了一次性搜索所有路徑從而求得最佳路徑,搜索效率明顯高出很多。

① 如果xi是“或節點”，它的子節點有(xj1,xj2,…,xjx)，則xi的代價計算公式如下：

h(xi)=min{c(xi,xj)+h(xjx)}

(1)

在這里取子集的最小代價值，當搜索最優路徑的時候，只需要代價值最小的節點。

② 如果xi是“與節點”，則xi的代價分為和代價法與最大代價法,如式(2)、式(3)所示。

(2)

h(xi)=max{c(xi,xjx)+h(xjx)}

(3)

由于本文中總代價等于每個故障源測試代價的總和，故采用式(2)帶入計算。

③ 如果xi是決策樹最低端的節點(已被隔離)，那么h(xi)=0。

④ 如果xi不可擴展，而且不是終端節點，則h(xi)=∞。

2 選擇系統擴展節點

此處介紹系統初始節點的擴展原理，由前述數學模型中的S與p，得到系統在初始狀態時的霍夫曼編碼，系統初始狀態的霍夫曼樹如圖3所示。

圖3中，圓為系統的狀態，圓下面標出的數字表示該狀態的p值。由圖3可計算出系統各狀態的霍夫曼編碼長度為w*=[5,7,5,5,7,7,2,5,5,5,5,7]，再由表1中相關矩陣，對系統初始節點S={s1,s2,…,s12}進行擴展，根據11個測試得11個解,樹擴展結果圖如圖4所示。

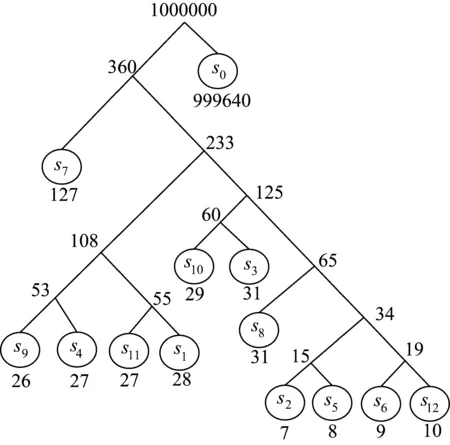
圖3 信息處理系統初始狀態對應的霍夫曼樹

圖4 初始節點擴展圖

圖4中，G為通過測試的信息處理系統狀態的集合；NG為沒有通過測試的信息處理系統狀態的集合[10]。

在初始故障狀態集S={s1,s2,…,s12}中進行測試tj(1≤j≤11)后，容易知道d0j=0(j=1,2,…,11)[1]。

由式(1)可知其解樹的代價估計值如下：

h*(xi)=min{cj+h*(x,tj)}

(4)

式中，cj為測試tj的代價;h*(x,tj)為應用子節點tj對x進行隔離的代價，由于x是tj的子節點，所以“與節點”(x,tj)的代價值是h*(x,tj)。因此根據式(2)可得：

h*(xi.tj)=p(xjp)h*(xjp)+p(xjf)h*(xjf)

(5)

式中，xjp為通過檢測的故障子集；xjf為沒有通過檢測的故障子集，而且xjp∪xjf=x(j=1,2,…,n)。結合式(4)和式(5)可得任意狀態集節點x的估價值如下[1]：

h*(x)=min{cj+p(xjp)h*(xjp)+p(xjf)h*(xjf)}

(6)

式中,h*(xjp)和h*(xjf)分別是節點xjp和xjf估價值的啟發函數[11]。由式(6)可以看出，在全部的擴展子節點中，狀態集節點的估價值是最小的。式(6)中，p(xjp)和p(xjf)分別由式(7)和式(8)計算：

(7)

(8)

基于霍夫曼編碼理論的啟發函數在與或圖中的搜索效率效果良好[12]，由式(9)表示：

(9)

(10)

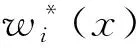
同理可計算出各節點xjp的啟發函數值，如表2第3列所示。

由式(6)計算各測試項的估價函數值，例如測試項t1的h(s)為：h(s)=c1+h(x1p)p(x1p)+h(x1f)p(x1f)=1+4.06×0.000332+5×0.000028=1.001487，經過計算，各個測試的估價函數值見表2第4列，由于整數位都是1，所以該列僅列出了h(s)的小數點后6位。

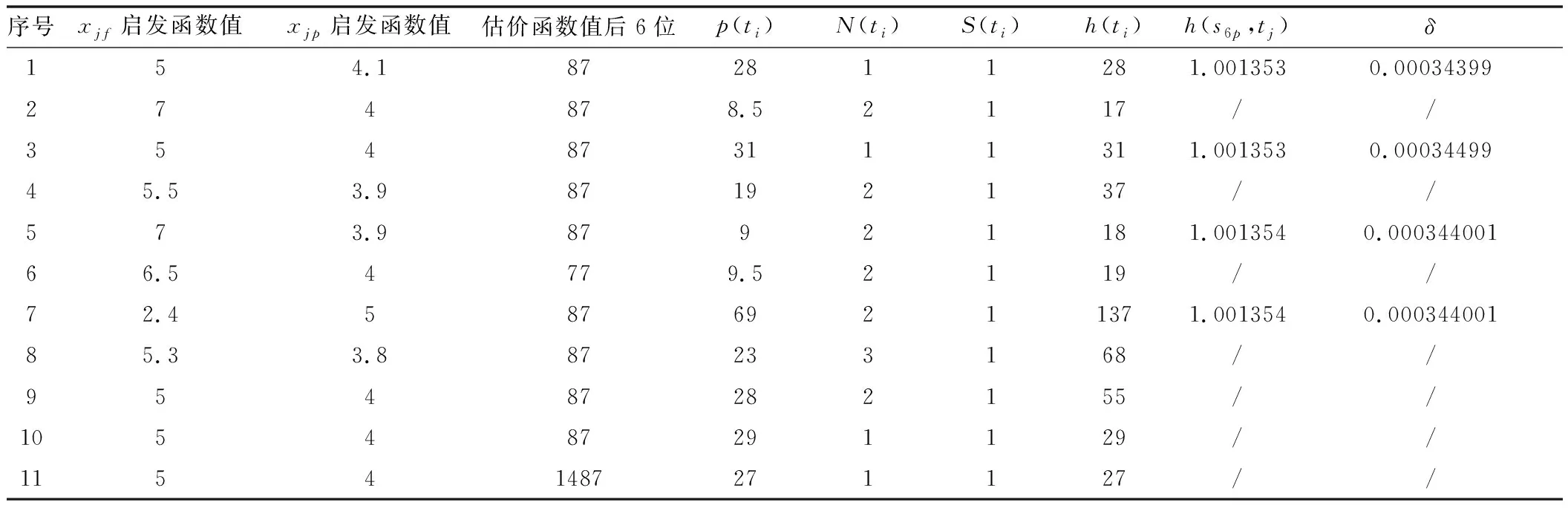
表2 各節點計算結果一覽表

根據表2中第4列的真實值，將個測試的估價函數值繪制成曲線圖，如圖5所示。

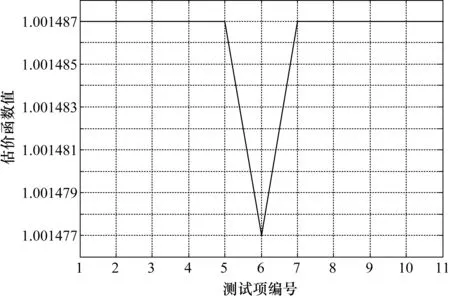
圖5 各個測試的估價函數值曲線

由圖5可知，最小估價函數值屬于t6，所以搜索最佳路徑時，t6就是搜索首節點。然后再分別擴展t6的兩個子集，繼續對最佳路徑的節點進行搜索。

3 擴展測試集的優選

首先確定優化完成后測試集中測試項的數目。然后再確定N個群落中的粒子數。第i個粒子的速度值和位置為：vi=(vi1,vi2,…,viD)和xi=(xi1,xi2,…,xiD)，i=1,2,…,N。群落中粒子的速度更新[1]和位置更新如下。

(11)

(12)

式中，w為慣性權重；c1為粒子的自我認知程度；c2為粒子對整體的認知程度；ξ、η為區間[0,1]內的隨機數；r為速度的約束參數[1]。

w值的大小決定粒子群算法的局部搜索能力；本文考慮到粒子的位置和速度優勢與整個群體的優勢，取w=1,c1=2,c2=2[1]。

以上是傳統的做法，本文未使用式(12)，使用了離散粒子群算法算法，在該算法中，粒子的速度值介于[0,1]之間，在代碼中借助式(13)實現[0,1]的值域值：

s(v)=(1+ev)-1

(13)

式(13)是每個粒子的速度更新公式，粒子的位置更新見式(14)。

(14)

式中，rand為[0,1]區間的隨機數。

基于以上所述，本文設計了測試項評價函數見式(15)，可根據式(15)對測試項相對于各測試發生概率的重要性做出評估[1]。

(15)

式中，p(ti)為系統所有可能發生故障的平均概率；N(ti)為ti能夠檢測到的故障數；S(ti)為系統所有故障中故障的最小可測度；a為調節值，本文中取a=1。通過表1得到測試項的評價函數值如表2第5列、第6列、第7列、第8列所示。

由表2第5～8列數據，可以看到任意一個測試項的重要性。為評估測試集的優劣，給出式(16)：

(16)

式中，Ts為隨機選擇的測試集；T為信息處理系統所有的測試項；N為Ts的數目；ηFD為系統的故障檢測率；ηFI為系統的故障隔離率；ci為測試ti的費用；h(ti)為測試ti的評價函數值[13]。

結合本文研究的測試序列優化問題將離散粒子群算法的粒子定義為一個二進制向量xi=(xi1,xi2,…,xiN)[1]，計算粒子在位置的速度值，位置更新按式(14)計算。

4 實驗驗證

本文通過編寫C++代碼，多次運行算法程序，識別狀態集s6p的測試集，多次運行算法的結果如圖6所示。

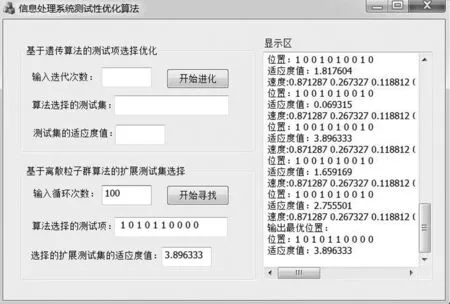
圖6 離散粒子群算法運行結果

算法運行結果中，位置若為1，則表示選中對應的測試，若為0，則表示未選中對應的測試。由圖6得，{t1,t3,t5,t7}為算法最后優選出的測試集。

接下來對t1,t3,t5,t7擴展即可，不需要對其他10個測試操作，從計算量來說，明顯縮減。

表2第9列、第10列中，h(s6p,tj)為測試tj對s6p的估價值，δ為新的估價值與原來估價值的差值。圖7繪制了優選測試的估價函數值曲線。

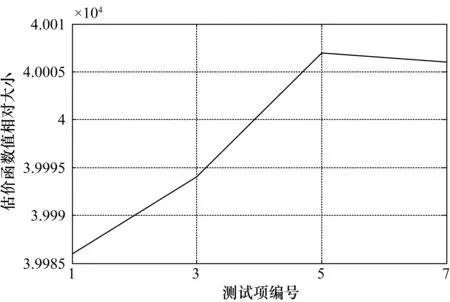
圖7 優選測試的估價函數值曲線

由表2第9列和圖7得：最小的評估函數值是t1，所以t1就可以被當做隔離出來最好的子集。類似地，擴展s6f={t6,t12}，并用DPSO算法優選出將要擴展的系統測試項集合{t2,t4,t5,t7}(備選測試集不包括t1)，其中t1為測試代價最優。接著擴展t1的一個子集s1p={s2,s3,s4,s5,s7,s8,s9,s10,s11}，結果如圖8所示。

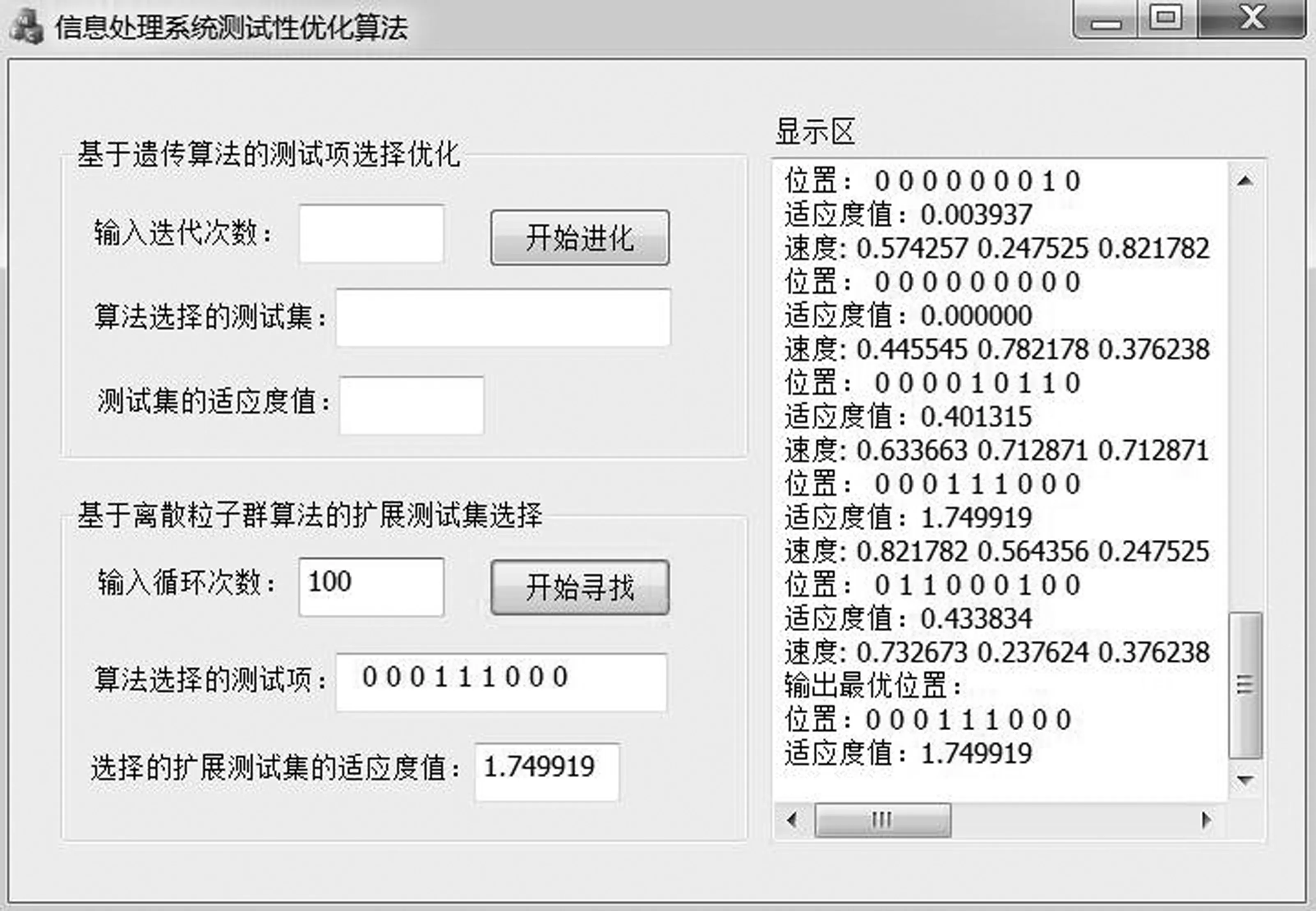
圖8 離散粒子群算法運行結果

由圖8得：{t5,t7,t8}為優選出的測試集，估價函數值最小的是t5。然后對s1f進行擴展，用DPSO算法選擇s1f將要擴展的系統測試項集合，得到信息處理系統最優測試策略決策樹如圖9所示。

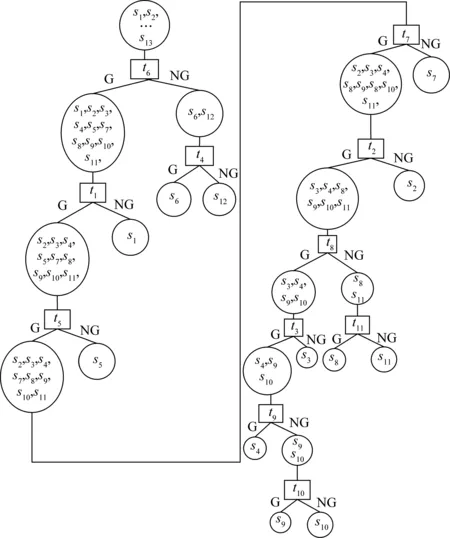
圖9 信息處理系統最優測試策略決策樹

基于以上整個過程，本文顯著減少了計算量，同時基于DPSO算法本身具有獨有的優勢，系統每一次進行的優化選擇都是全局最優。

5 結論

由圖9可得：該復雜信息處理系統所有的故障都能被獨立隔離。按照圖9對故障進行定位，可使故障源迅速確定，同時保證理論上總的測試代價最小。

當系統同一時間只發生了一個故障，可由圖9中的測試順序，利用一次測試即可將故障源定位。若多個故障同時發生，或存在隱藏故障時，也可利用圖9進行故障定位，只需進行多次測試，將故障一一定位。