認知無線網絡的Rubinstein博弈頻譜共享方法研究

(蘭州理工大學計算 機與通信學院，甘肅 蘭州 730050)

近年來，隨著移動無線通信技術的快速發展，用戶對網絡的服務類型和QoS不斷提高。新的無線通信技術對無線通信帶寬需求也提出了更高的要求[1]。致使通信系統的設計者和管理者不斷提高無線通信的頻譜效率、功率效率和系統容量等。根據美國聯邦通信委員會(FCC)的調查結果顯示[2]：在各個時間段和地區，只有15%～85%授權頻譜被有效利用，3 GHz以下頻段的平均利用率低到僅為5.2%。由此看來，當前的固定頻譜分配策略是造成頻譜資源利用率低下和網絡頻譜資源供不應求的主要原因。認知無線網絡具有感知無線通信環境、自適應調整傳輸參數(功率、載頻和調制方式)和有效地提高頻譜資源利用率等，都已被學者提出。

認知無線電網絡技術頻譜管理是提高頻譜資源利用率的關鍵環節，其常與經典的數學理論和微觀經濟學模型相結合，來優化用戶的頻譜資源分配問題[3]。在各種復雜的數學模型中，被提及最多和應用最多的就是博弈論模型。在博弈論模型中，參與者為了使自己的收益達到最大，會對自己的策略進行選擇和比較。基于此特性，將博弈論與認知無線電網絡中主用戶、次用戶對于頻譜的使用很好地結合,并使得整個系統具有高度的自組織、自學習和自適應能力。

博弈論解決動態頻譜分配方法受到了學者廣泛關注，文獻[4]提出了一種分布式頻譜共享算法，針對認知用戶的“自私行為”提出了懲罰機制,并通過價格反饋機制，保證了主用戶和認知用戶的最大效用，提高了頻譜資源的利用率。文獻[5]設計了一種基于演化博弈的頻譜共享機制，充分考慮了認知無線電網絡具有動態、異構等特點和無線信道不可靠、易受環境影響等因素，確保認知用戶之間頻譜共享的公平性。文獻[6]提出了一種基于合作重復博弈的認知無線電頻譜共享算法，實現了在兩個認知用戶的環境下，頻譜共享速率收益的最大化。文獻[7]針對遠近效應、路徑消耗等問題提出了一種新的功率算法，在效用函數中增加鏈路質量和主用戶干擾容下等因素，保證了認知用戶在網絡中的公平性。文獻[8]針對Underlay接入方式的功率控制進行研究，在解決認知用戶功率控制問題的同時，考慮頻譜分配算法，滿足對吞吐量和時延要求不同的各類用戶。文獻[9]在雙人討價還價模型基礎上，并提出了在節點間相互干擾下的多人雙邊模型的頻譜分配模型。文獻[10]提出了一種基于主用戶干擾容限的多人雙邊博弈模型，通過動態無限博弈模型，得到子博弈精煉納什均衡。文獻[9]和文獻[10]中貼現因子設置為相同的定值，當通信系統性能變化時，需要重新設置，不能很好地體現認知技術的自適應性。

在上述學者研究的基礎上，本文提出了一種多人合作重復博弈模型；將經濟學中的貼現因子與通信環境建立聯系；將各個認知用戶的通信干噪比作為依據對用戶進行分類和排序，分析并推導認知用戶在此策略下的速率總收益，并進行實驗驗證。

1 博弈模型

1.1 羅賓斯坦(Rubinstein)博弈

Rubinstein博弈模型是一種聯盟內參與者信息互通的動態博弈。假設聯盟中存在兩個參與者A和B，共同劃分一塊總面積為“1”的土地，A先提出分配方案，即“出價”；由于聯盟中信息是互通的，B根據A的“出價”選擇接受或者拒絕，如果拒絕，B再提出自己的分配方案，即“還價”，然后再由A考慮是否接受，以此類推，直到兩個參與者之間達成妥協。

上述博弈過程中將會有無限多個納什均衡，但只有一個“子博弈精煉納什均衡”。文獻[11]中提出在無限期議價博弈中，先開價者將獲得比后開價者更大的受益(份額)，且對議價雙方而言，誰貼現因子大，耐心程度越大，均衡結果對其越有利。所以當參與者A先出價時，A將是最大的受益者。由文獻[9]可知子博弈精煉納什均衡結果，即A和B最終分得的份額為

(1)

(2)

式中，δ1，δ2分別為參與者A和B的貼現因子。

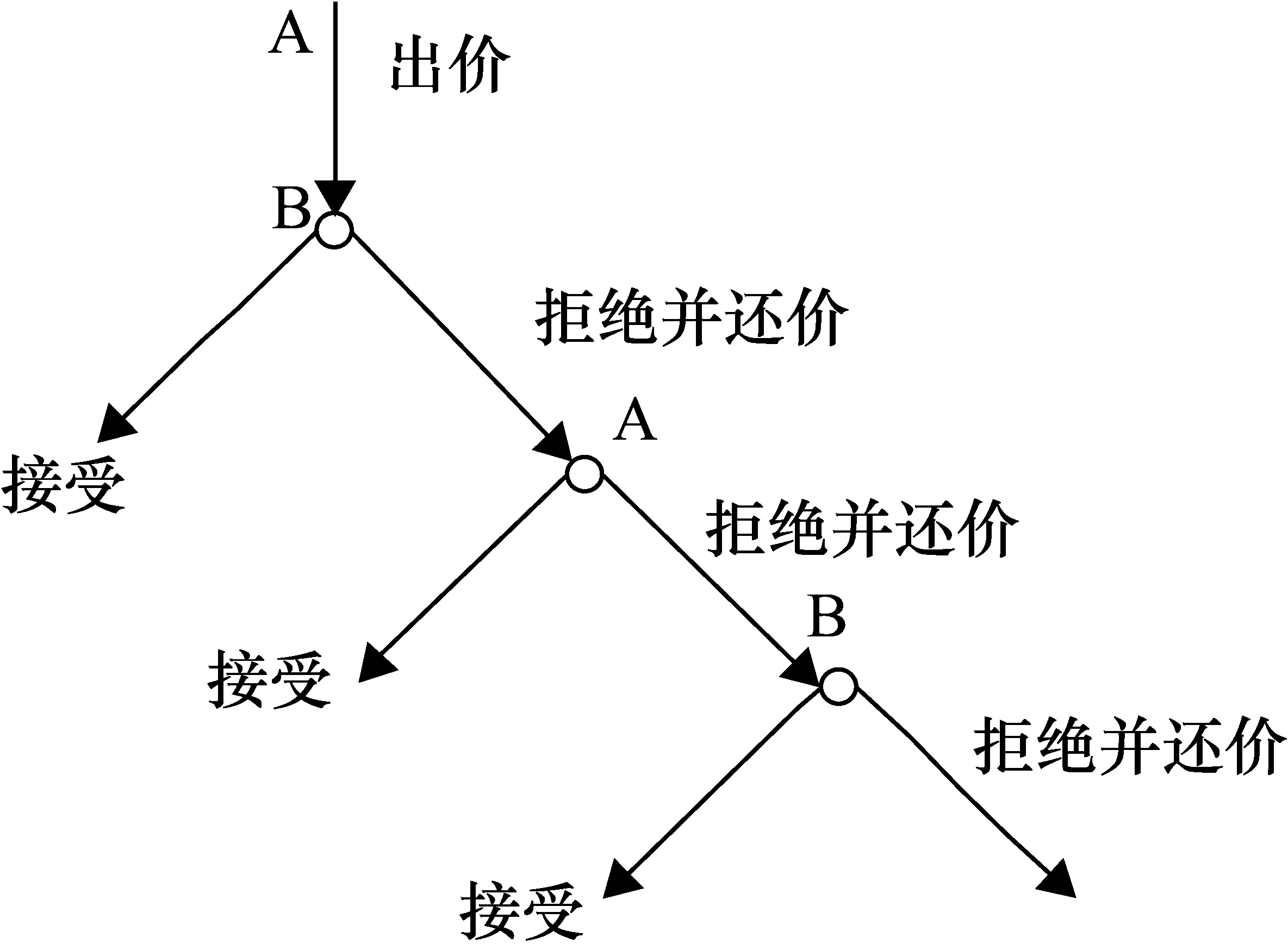
圖1 輪流出價的討價還價模型

1.2 多人雙邊博弈模型

本文考慮在歸一化信道帶寬模型下，N個認知用戶的頻譜分配問題。博弈模型中各個要素如下：

①N個認知用戶為博弈過程中的參與者即決策主體，用SU1,SU2,…,SUN表示，對應的貼因子為δ1,δ2,…,δN。

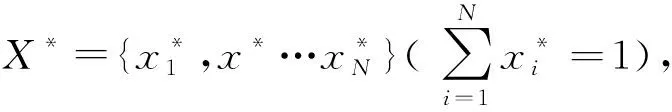
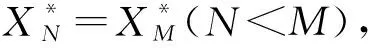
在N個參與者的討價還價博弈模型中，N個參與者按順序向下一個參與者“開價”，下一個參與者選擇接受或者拒絕。當下一個參與者選擇接受時，則繼續按序“開價”；選擇拒絕時，子博弈結束，進入下一個子博弈過程。

假設子博弈由SUi開始，向SUi+1提出SUi分得份額xi，SUi+1選擇接受或拒絕。兩種情況下的具體描述為：

① 若SUi+1接受，SUi獲得xi并不參與接下來所有的子博弈過程。而SUi+1就剩下的資源，繼續找SUi+2，SUi+1提出分走xi+1。

② 若在當前的子博弈中SUi拒絕，則當前的子博弈結束，進入下一個子博弈過程。并由SUi+1最先開始出價。

基于上述分析，子博弈過程可表示為

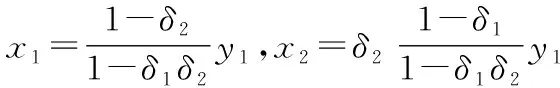
(3)

其中，xi=x′i，yi為引入中間變量，由式(3)可得

(4)

達到子博弈精煉納什均衡時，各個參與者之間策略的關系為

(5)

得到各個參與者之間的策略關系后，認知用戶將以此為依據對頻譜進行分配。

2 基于多人雙邊博弈頻譜共享算法

2.1 功率控制模型

考慮單蜂窩小區的中心輻射式認知無線電網絡系統，對認知用戶進行上行功率控制，在該系統中有M個主用戶，N個認知用戶和一個基站，假定一個用戶只包括一個收發設備，基站負責頻譜空穴檢測和頻譜資源分配。

設第i個用戶的擴頻帶寬為WHz，傳輸速率為Rib/s，發射功率為pidBm，認知用戶i到基站的鏈路增益為hi，主用戶k到認知用戶i的鏈路增益為gk,i，基站處的背景噪聲為σ2。則第i個認知用戶在基站處的信干噪比定義為

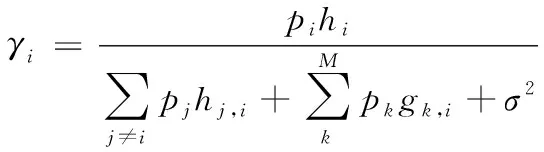
(6)

考慮不同的認知用戶共享頻譜資源存在不同的QoS需求差異和非負凸函數的極值存在問題,采用文獻[12]中的效用函數

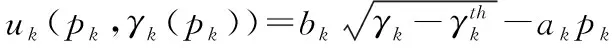
(7)

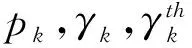
效用函數由兩部分組成，前一部分是以超過目標信干噪比的差值為變量的冪函數，表征認知用戶對信干噪比的滿意程度；后一部分是價格函數，為了防止認知用戶的“自私行為”；不顧及其他認知用戶的收益情況下，一味地增大自己的發射功率來提高自己的信干噪比。通過價格函數的建立，強迫認知用戶進行“合作”。

根據文獻[13]得到關于功率控制下最優功率的迭代公式

(8)

依據迭代后的最優功率得到各個認知用戶最終的信干噪比，并通過最終的信干噪比基于映射關系得到每個用戶在博弈中的貼現因子。

2.2 頻譜共享模型

在傳統的增大認知無線電網絡用戶速率的方法中，通常是基于對認知用戶在發射功率和基站干擾不超過給定閾值的約束條件下，對于認知用戶的功率進行控制，進而最大化各個認知用戶的信噪比以得到各個用戶的最大傳輸速率。

由香農公式可知，認知用戶的最大信息傳輸速率，不僅與用戶的信噪比有關，還與認知用戶分配的信道帶寬有關。本文利用上述思想在傳統的功率控制算法上，加入多人雙邊的博弈模型，來最大化認知無線網絡中的總用戶速率收益。

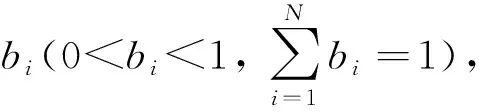
ci=bilog2(1+γi)

(9)

其中，bi為分配給認知用戶i的帶寬，由上述的博弈模型得

(10)

貼現因子與鏈路質量之間的映射關系為

δi=αγi

(11)

其中α為認知用戶的信干噪比γi與相對應的用戶貼現因子δi之間的調整因子。

認知無線電網絡系統的總的信息傳送速率

(12)

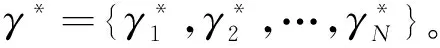
(13)

多人雙邊博弈頻譜分配算法具體步驟如表1所示。

表1 多人雙邊博弈頻譜分配算法具體步驟

3 仿真實現與分析

為了驗證上述理論，在Matlab軟件平臺下進行仿真實驗。仿真參數如下：歸一化信道帶寬為1，每個認知無線電網絡中包含6個次用戶和2個主用戶，每個認知用戶隨機分布在[500 m,1500 m]之間,初始功率為1×10-3dBm，收到的帶內噪聲為5×10-6dBm；主用戶隨機分布在[10 m，50 m]之間，初始功率為5×10-6dBm。處理增益為2，擴頻帶寬和傳輸速率分別為1×106和1×104，目標信干噪比γtar=7 。

在傳統的功率控制算法下，各個地理位置不同的認知用戶發射功率的變化情況如圖2所示。由圖可知，為了確保主用戶的正常通信，6個認知用戶初始設置的發射功率由于效用函數的建立，經過一次牛頓迭代算法后有一定的降低。各個認知用戶為獲得利益最大化，在主用戶的干擾容限范圍內，認知用戶的發射功率在第二次迭代式有一定的增大，然后到達穩定狀態。這樣既能保證主用戶的正常通信，也能使認知用戶得到最大的吞吐量。

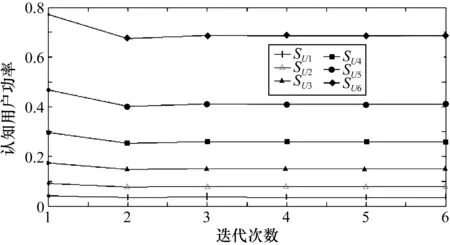
圖2 功率控制算法下的認知用戶的發射功率

各個認知用戶與其發射功率相對應的信干噪比的變化情況如圖3所示。由于受到主用戶、認知用戶之間和帶內噪聲的干擾，不同地理位置的認知用戶在第一次迭代時達到各自信干噪比的最大值；在第二次迭代時，信干噪比隨著發射功率的降低而降低；最后隨著發射功率的回升而有所提高并趨于穩定。

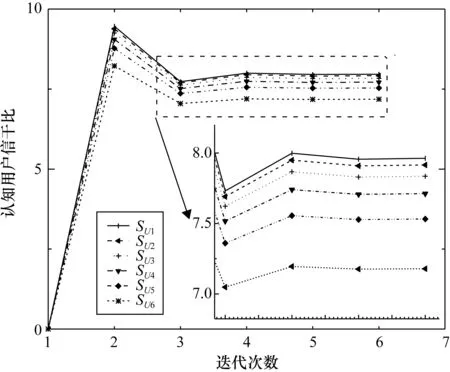
圖3 功率控制下的各個認知用戶的信干噪比

基于多人雙邊博弈模型的頻譜共享算法的6個認知用戶的收益情況如圖4所示。在博弈模型下，首先根據認知用戶的信干噪比對認知用戶進行排列，確定各個認知用戶的博弈順序。然后，建立信干噪比與貼現因子之間的映射關系，即信干噪比越大的認知用戶鏈路質量越好，作為“獎勵”，給予其較大的貼現因子值并能獲得更多的收益。

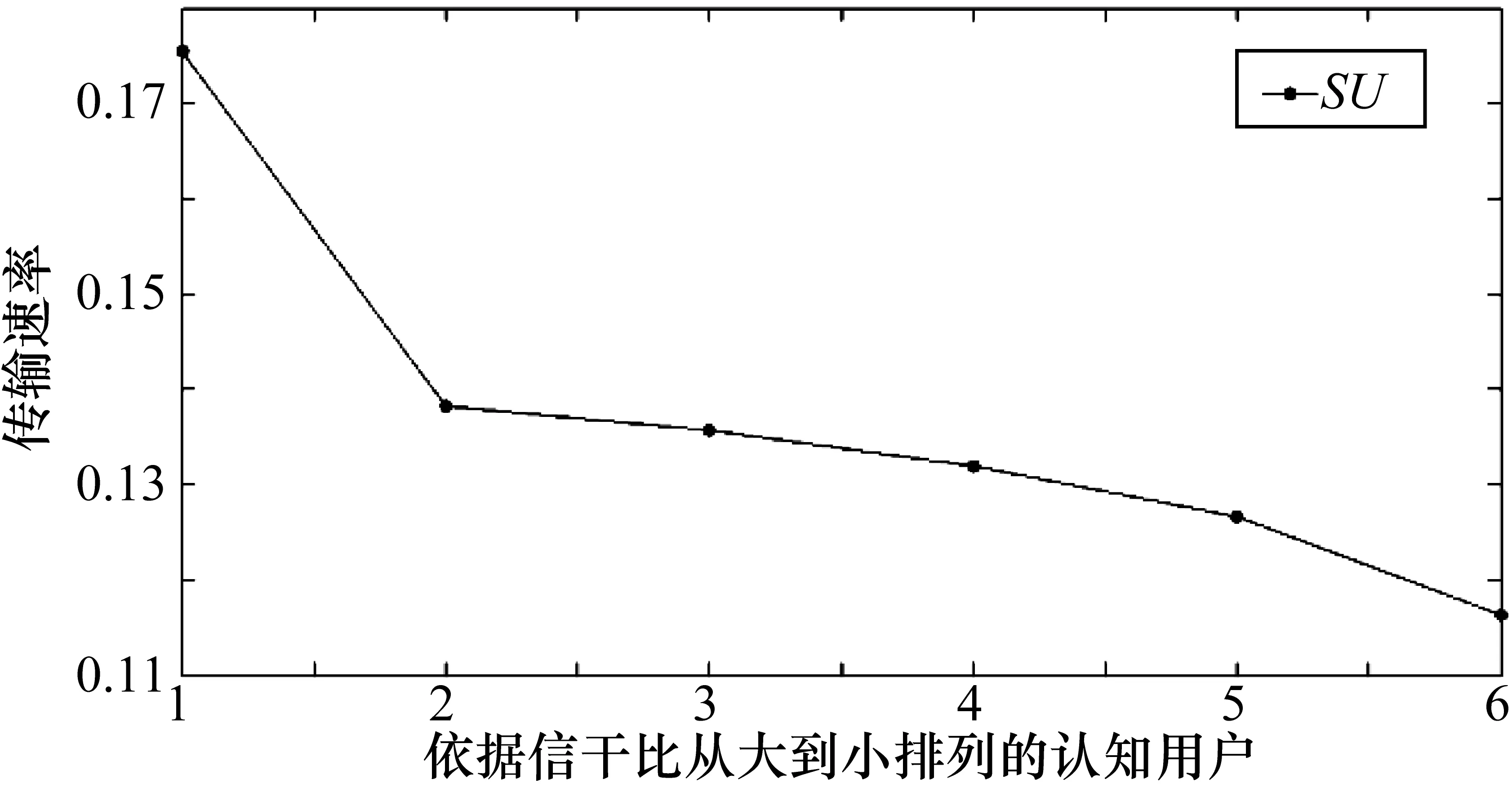
圖4 多人雙邊博弈模型下的認知用戶的收益

分析對比在歸一化的信道帶寬的情況下，基于多人雙邊博弈模型的認知無線電網絡的總體收益和信道帶寬隨機分配時的收益情況如圖5所示。① 實線：基于多人雙邊博弈模型下，認知無線電網絡20次總體的傳輸速率。可以看出，在博弈模型下，認知無線電網絡的傳輸速率一直處于一個較高且穩定的狀態。② 虛線：當信道帶寬隨機分配時，總的傳輸速率的變化情況。每一個節點表示系統總的收益，每一次實驗得到6次系統總的收益結果，將4次頻譜隨機分配實驗的結果與本文的算法進行比較。由圖可以明顯觀察到本文算法得到的系統總收益趨于穩定且都高于隨機分配時系統收益。由此可見本文算法對于認知無線電網絡總的傳輸數率的提升。

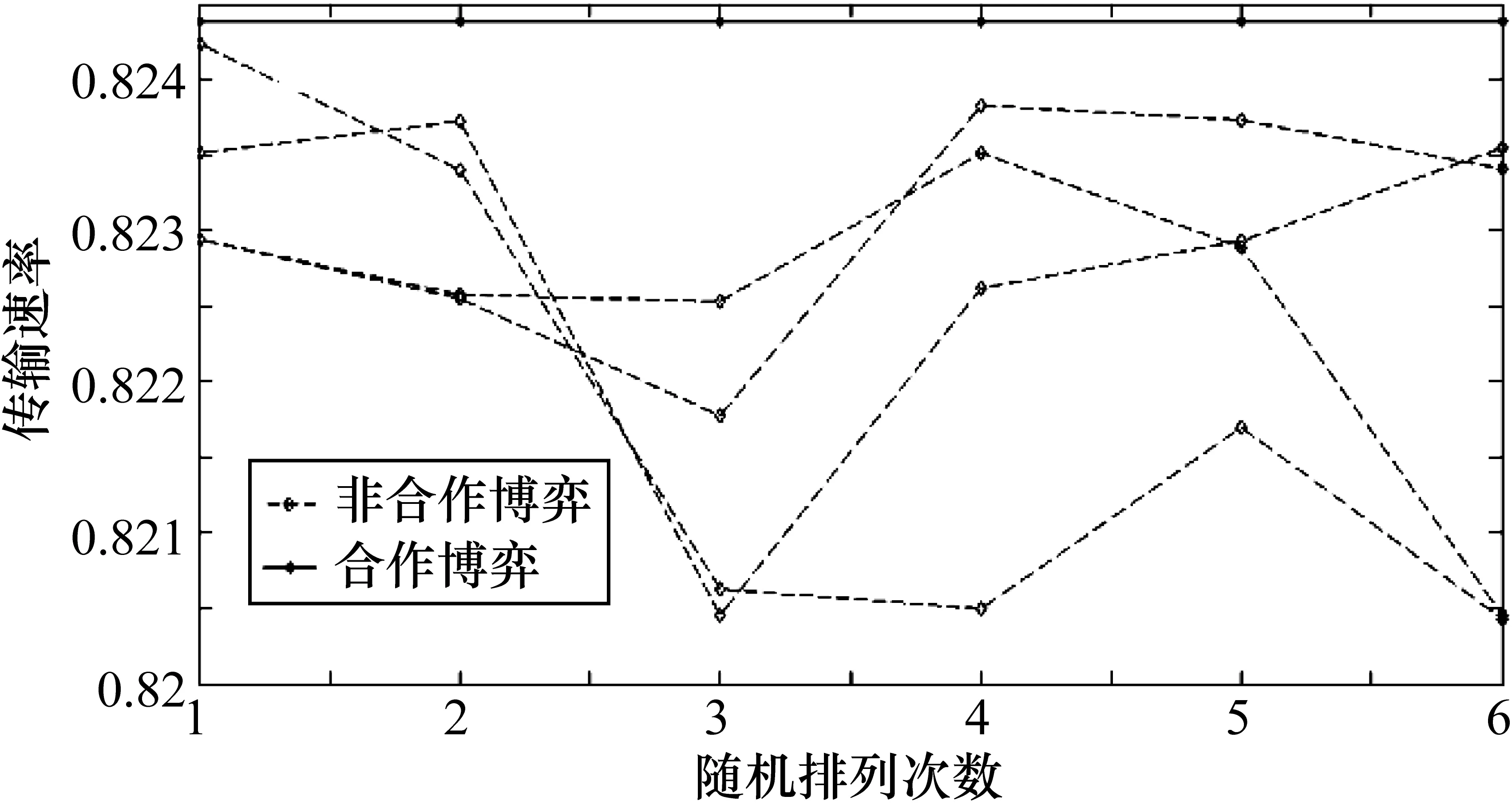
圖5 基于博弈模型和隨機分配時網絡收益對比

為了衡量本文算法對頻譜分配即時性好壞的指標，做了兩種分配方式下時耗的對比試驗,結果如表2所示。選取了3組博弈模型和隨機分配兩種算法下，認知無線電網絡在頻譜分配時所消耗的時間。從表2中可以看出相比于隨機分配，博弈模型下的頻譜分配算法可以節省一半以上的時間，對時延敏感業務是很好的提升，博弈模型下的頻譜分配算法的即時性更好。

表2 頻譜分配時間對比 單位：s

4 結束語

本文針對傳統的功率控制算法為了降低干擾而影響認知用戶的QoS的問題，提出了多人雙邊博弈模型下的頻譜分配方法。為了提高方法的自適應能力，將信干噪比與貼現因子建立映射關系并依據信噪比對認知用戶進行排序，得到不同信干噪比下的認知用戶的收益情況。通過本文的博弈算法與信道帶寬隨機分配下的網絡總收益進行對比后發現，認知無線電網絡的整體傳輸速率總收益得到了明顯的提升并對頻譜分配時間有很大的改善，在提高用戶吞吐量的同時也對系統即時性進行了提升。文中僅將信干噪比的大小作為評價信道質量好壞的主要標準，但實際的通信環境十分復雜，信道也將受到多種因素的干擾。下一步將對多種因素影響下的通信信道進行研究，綜合考慮時間、空間和各種干擾下的鏈路質量,并對不同的影響因素設置合理的權重，使各個認知用戶對頻譜的劃分更加公平。