飛機高原機場起降能力研究與分析

韓濤鋒，冷智輝，劉 晗，岳定春

(航空工業洪都，江西 南昌，330024)

0 引言

我國幅員遼闊，地形多樣，但僅四大高原占地就超過國土面積一半，其中青藏高原占地250多萬平方公里，與7個周邊國家相接壤。高原機場地理位置特殊，周邊環境及氣象條件惡劣，飛機在高原機場執行任務進行起降尤為困難，不僅操作復雜，受外界影響因素也較多，對高原機場飛機的起降特點與能力研究顯得格外重要。

當前我國列裝有多型多系列飛機，其中也不乏舊型號飛機，這些飛機在研制初期因條件限制，僅有標準大氣條件下的少量推力、油耗數據，如今再通過高空臺試驗獲取其他高度和溫度下的數據已不太現實[1]，這對該類飛機的高原起降能力分析帶來了很大困難，同時也影響到該類飛機進駐高原機場的任務決策，國內對這方面的研究有著較大需求。目前國內外對高原機場起降能力的研究較少[2-3]，在高原條件下飛機的發動機推力、油耗數據理論推導方面，現有方法也僅局限于海拔高度H=0～2公里，M=0～0.6范圍內，無法適用于如青藏高原等高海拔地區（平均海拔達到3500m）。為拓展飛機的能力，同時滿足國家和社會使命任務要求，開展高原機場飛機的起降特點與能力研究非常必要。

基于這一現狀，本文首先對飛機在高原機場的起降能力與特點進行了分析和研究；結合飛機發動機特性，提出了一種適用于評估飛機高原起降能力的方法；通過建立飛機起降能力模型，分別用工程估算法和文中提出的方法，經理論推導和計算，得到某型飛機的高原起降性能參數；最終通過在某海拔接近4000m的高原機場進行飛行驗證，將理論推導結果與實際試飛值進行了對比。

1 高原機場起降能力與特點分析

相較平原，高原地形復雜、空氣稀薄、氣壓低、氣候多變，飛機的起降能力面臨巨大挑戰，具體體現在：

1）高原大氣密度小，導致發動機進氣量少，推力減小，飛機的加速和爬升性能較平原機場明顯下降；

2）相同表速對應的真空速和地速變大，相同重量下起飛離地和著陸接地真速都比平原大[4]；

3）發動機推力顯著下降導致起飛滑跑距離變長；

4）飛機接地后阻力小、減速慢，導致著陸滑跑距離變長；

5）起飛、著陸過程中抗側風能力變差；

6）相較平原機場，高原機場飛機最大允許起飛和著陸重量受到較大限制；

7）空氣密度減小導致作用在舵面上的作用力減小，飛機在高原機場的操縱性變差；

8）飛機發動機、輪胎、輪轂等高溫成附件的散熱能力變差，極易出現輪胎甩胎面、胎肩胎圈脫層、鼓泡等故障，輪胎、剎車系統的消耗加快。

由于起降能力的巨大變化，導致飛機在高原機場的起降特點及起降注意事項與平原相比也有諸多不同：

1）起飛滑跑過程中，不宜過早抬前輪，否則會影響飛機加速性，抬前輪速度控制在離地速度的80%～90%；

2）起飛時，應控制好飛機離地迎角，一般7°～8°為宜。迎角太小導致起飛滑跑距離過長，對輪胎和跑道提出更高要求，迎角太大會導致飛機提前離地，離地后的速度過小會導致橫航向姿態不易控制；

3）離地后，維持飛機上升姿態，柔和控制駕駛桿。因發動機推力下降較多，飛機離地后上升和增速緩慢，且離地后不夠穩定，不能急于帶桿上升，以防拉桿過頭引起失速；

4）高原空氣稀薄，輪胎散熱慢，為防止輪胎在空中漏氣、爆胎，危及飛行安全，飛機離地后需帶起落架于低空飛行1～2分鐘用于降溫；

5）高原機場著陸真速大，轉彎半徑增大，下滑時間相對縮短，進入四轉彎的時機應適當提前；

6）飛機加、減速特性變差，四轉彎后要及時調整下滑速度，掌握好提前量；

7）因著陸拉平前的真速大，拉平階段下降率和半徑增大，因此拉平開始的高度應適當提高 （一般20m左右），下滑點和拉平點都應適當后移（下滑點比正常后移100m左右）。拉夠飛機接地姿態，盡量控制好接地迎角（7°～8°左右），接地迎角太大或太小均不宜，原因與起飛相同；

8）為防止輪胎剝皮，減少輪胎磨損，應嚴格控制飛機著陸重量和著陸速度，防止目測著陸速度過高；

9）收油門和拉桿必須準確配合，防止過快收光油門；

10）高原機場空氣密度小，不利于剎車散熱，飛機著陸接地停機后仍需對輪胎和輪轂進行液氮降溫或其他方式降溫，降溫持續時間不得少于20min；每次飛行結束后，必須在地面停留至少30min，經檢查確認輪胎保險塞未熔化、剎車溫度沒有超過限制后方可正常起飛。

2 “相似原理”外推法概述

針對部分機型缺少非標條件下的推力、油耗數據情況，若進一步研究其高原起降能力，首先需完成其在高原機場的推力、油耗數據的理論分析與推導。與平原相比，高原環境較惡劣，影響因素也多，目前在已公開的文獻及老一輩專家的研究文稿上鮮有針對機場海拔高度超過2000米的研究。考慮到大氣溫度和壓力對發動機特性的影響，本文采用“相似原理”外推法，即在原有的發動機數據基礎上，通過引入修正系數的方式[2,5]推導估算出飛機在高原機場的推力、油耗數據。

首先，設定飛機進氣道總壓恢復系數，在保證飛行M數和相對換算轉速這兩個參數相同的情況下，認為發動機工作狀態“相似”。

第一步，根據當地即時的大氣靜壓、大氣靜溫以及發動機轉速求出對應速度下的大氣總壓、大氣總溫與相對換算轉速：

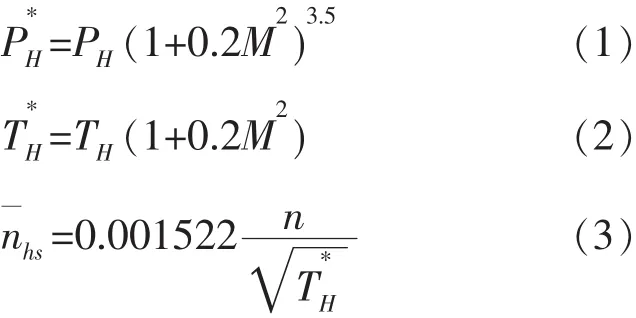
其中，PH、TH、n分別為大氣靜壓（kg/cm2）、大氣靜溫（K）以及發動機轉速（轉/分）分別為大氣總壓（kg/cm2）、大氣總溫（華氏度）及相對換算轉速（轉/分）。

第二步，通過查閱發動機專用技術手冊，根據與飛機發動機相對應的空氣流量曲線及推力和耗油率曲線，外推出與相對換算轉速相對應的換算推力Rhs、換算耗油率CRhs和換算空氣流量GKhs；

第三步，將一、二步中得出的結果代入發動機專業公式中：

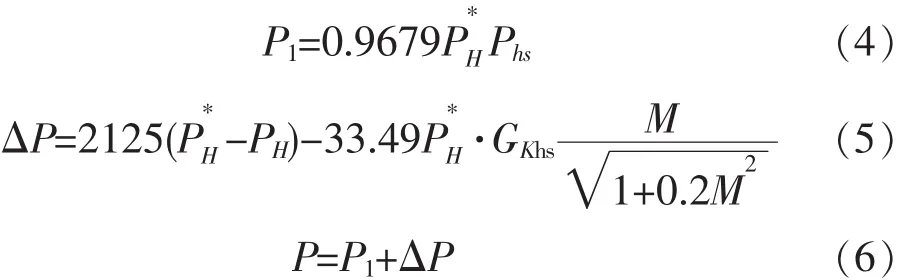
由此計算出發動機推力P（公斤）。

進一步通過分析和計算，可得出耗油率

空氣流量

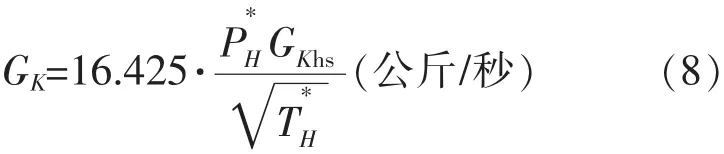
最后，通過將外推和計算分析得出的推力、油耗與飛機技術手冊中標注的飛機發動機推力、油耗數據進行對比，得出某型機在高原非標條件下的發動機推力、油耗修正系數 K1、K2，即 K1=P/P0，K2=CR/CR0（P0、CR0均為飛機技術手冊中標注的飛機發動機推力和耗油率）。

在某固定場溫條件下，外推出的推力修正系數K1與油耗修正系數K2與機場高度的變化關系如表1所示。

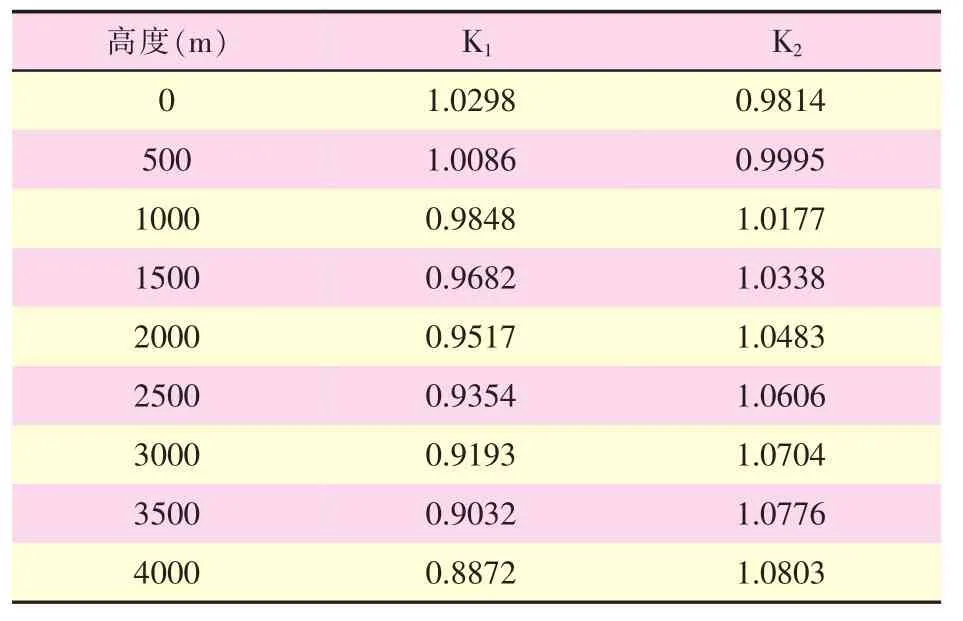
表1 推力、油耗修正系數

3 高原起降能力模型構建與理論計算

在地面滑跑時，飛機所受作用力包括重力、發動機推力、機輪與地面間摩擦力、氣動升力和阻力等，飛機受力情況如圖1所示。將以上各力分別分解到平行于跑道和垂直于跑道方向上，建立的數學模型為[6]：

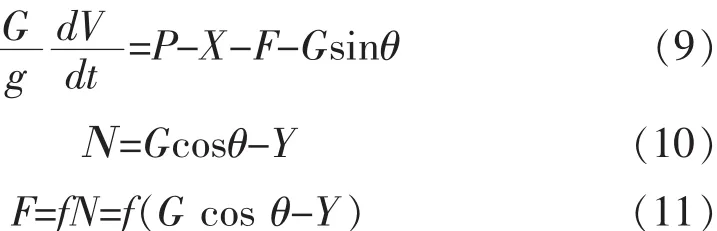
則

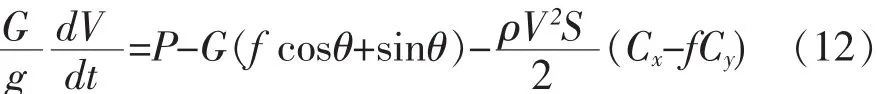
式中，G為飛機重量，g為重力加速度，V為飛機真空速，t為時間，P為發動機可用推力，X、Y分別為阻力和升力，F為機輪摩擦阻力，θ為跑道坡度（上坡為正，下坡為負），N為地面支撐力，f為摩擦系數，S為機翼面積，ρ為大氣密度，Cx、Cy分別為阻力系數與升力系數。

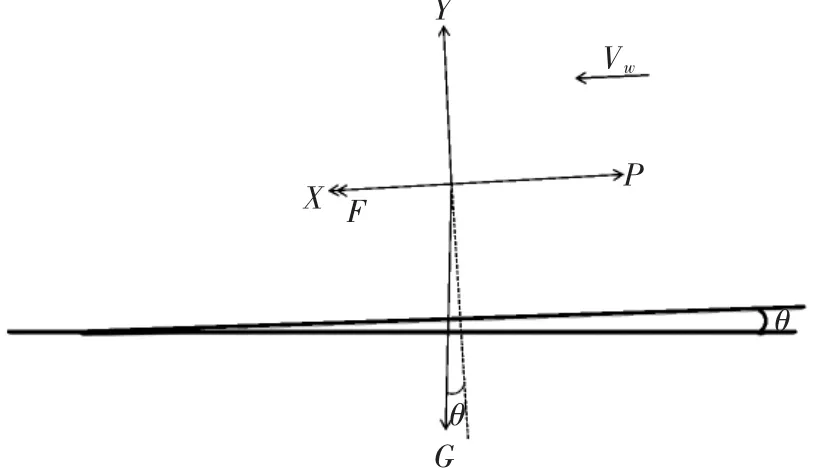
圖1地面滑跑飛機受力情況

在對飛機的起降能力進行粗略分析時，為方便分析，通常采用工程估算法進行計算，即假定飛機起飛滑跑為直線勻加速過程，平均加速度a采用速度方向作用在飛機上各個力的平均值計算得到；跑道坡度較小，近似認為 sinθ=θ；因氣動力部分(Cx-fCy)值較小，一般忽略該項[7-8]。因此直接對（12）式積分，并根據牛頓第二運動定律和飛行力學原理進行推導，即可得起飛滑跑距離公式：

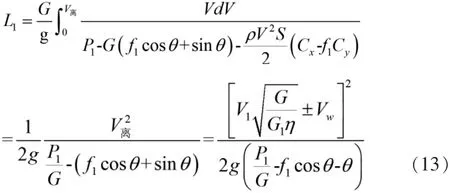
同理，可推導出飛機著陸滑跑距離公式：

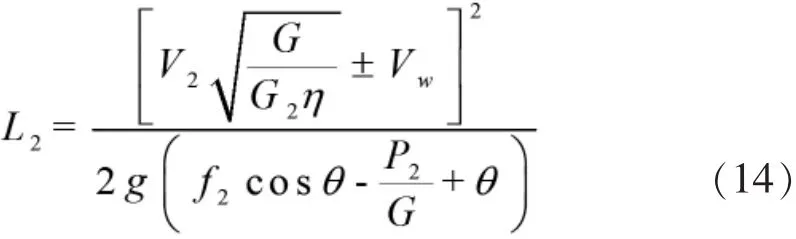
相對應的起飛離地速度和著陸接地速度分別為：

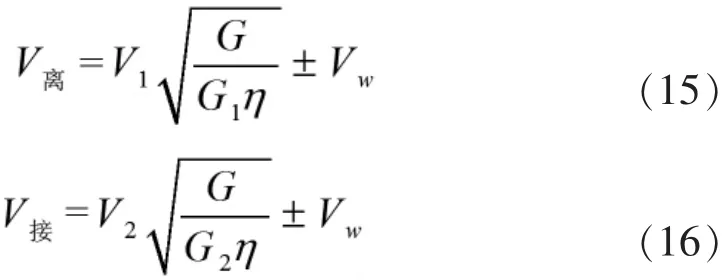
式中，P1、P2分別為起飛、著陸滑跑過程中作用在飛機上的平均推力，f1、f2分別為地面滑跑滾動摩擦系數和剎車折算摩擦系數，G為飛機的計算起飛（或著陸重量），G1（G2）、V1（V2）為從飛機說明書中查到的起飛重量（著陸重量）和相應的在標準大氣條件下的離地速度 （接地速度），η為空氣相對密度，Vw為分解到跑道方向上的風速，其中±號中順風取+，逆風取-。

在對飛機的起降能力進行精細分析時，通常將飛機的地面滑跑階段劃分為三輪滑跑段和兩輪滑跑段[7]，如圖2所示。

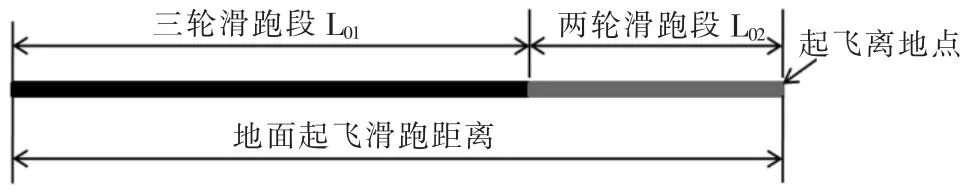
圖2起飛滑跑過程

通過對（9）～（12）式進行推導可得

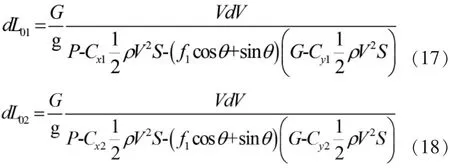
式中，Cx1與Cy1為起飛構型條件下對應于停機迎角的阻力系數和升力系數，Cx2與Cy2為離地迎角下對應的阻力系數和升力系數，由于兩輪滑跑階段迎角變化不大，視這一過程中升阻系數不變；通過對上述兩式進行數值積分求解，可得起飛滑跑距離

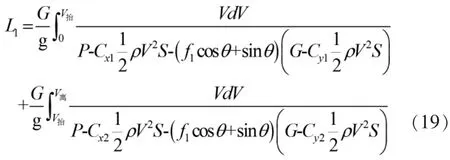
飛機的著陸過程可認為是起飛的反過程，飛機接地后，通常先要經過兩輪無剎車自由滑跑減速，一般需要2～3s[7]。然后放下機頭，前輪著地作三輪滑跑并使用剎車，假定剎車前的滑跑距離近似為3V接，則著陸滑跑距離L2可近似為：

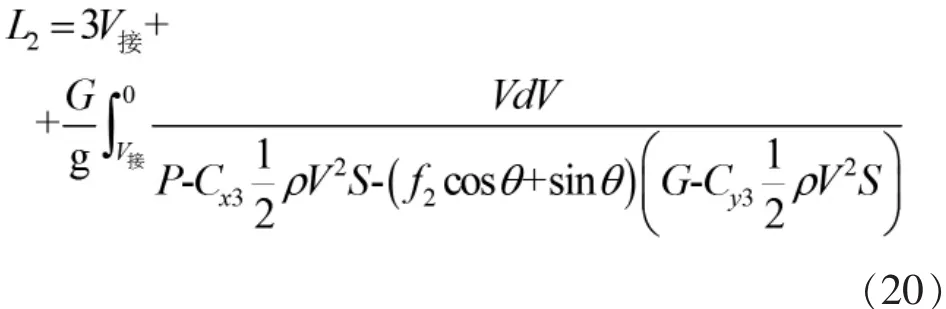
其中，

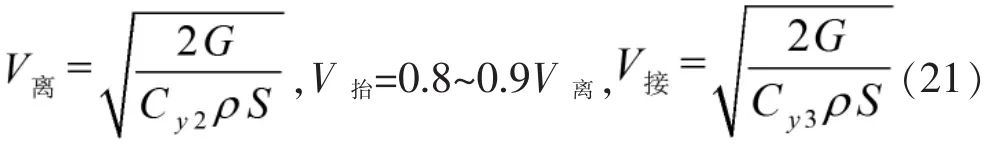
式中，V抬為飛機抬前輪速度，V離為起飛離地速度，V接為著陸接地速度；Cx3與Cy3分別為著陸接地迎角下對應的阻力系數和升力系數。

通過上述建立的模型和公式，可計算出飛機起降滑跑距離及起降速度。但由于實際飛行過程中的環境并不是理想條件，各種影響因素不可忽略，因此還需通過向（19）和（20）式中引入第3節中得出的推力修正系數K1與油耗修正系數K2，之后再進行計算以對計算結果進行修正。

4 飛行驗證與結果分析

高原氣候條件惡劣，任何一型飛機在高原機場的起降能力與在平原機場相比都會大大降低。由于某型飛機是首次且是在缺少非標條件下的推力、油耗數據情況下進駐高海拔高原，需關注的因素和參數較多，風險性大。為最大化降低試飛風險，依次采用預先數據研究、理論推導計算、平原試飛、次高原試飛、高高原外推性能計算、高高原地面滑跑試飛漸進修正再逼近的手段，分2～3步逐級開展試飛的方法最終才得以在某高高原機場完成試飛。

為盡可能準確測試出試飛數據，在跑道一側與跑道平行的一條直線上，依次找出與預計起飛離地點、著陸接地點及停止點相對應的位置，分別在這些位置前、后各250m區域，每隔50m插一面彩色旗，每連續5面旗（依次為紅黃藍綠粉5種顏色）為一組；在直線上對應的預計開始滑跑點附近布置一組旗，每2～3面旗的范圍由一人負責。當飛機由滑行道滑入跑道停止準備起飛時、飛機滑跑至離地點時以及飛機接地和停機時分別記錄下各點的位置及相對跑道起始點的距離S1、S2、S3、S4，后分別將幾個值相減即可得到飛機的起飛滑跑距離L1（或著陸滑跑距離L2）。

每一次試飛結束后，均將理論數據與試飛數據進行對比，若兩者相一致或試飛數據相對理論數據有安全余度且兩者差異不大，則可繼續開展后續試飛，否則需結合試飛結果對理論數據進行修正，重新評估其安全性后方可開展試飛。

圖3～圖5中分別將工程估算法、“相似原理”外推法得出的結果與實際試飛結果進行了比較。

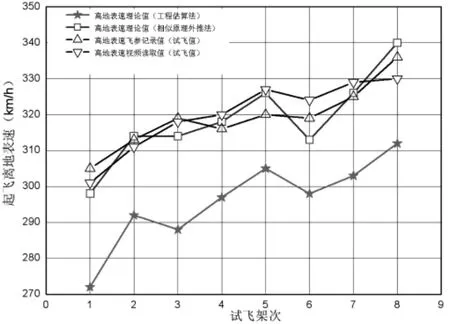
圖3起飛離地表速

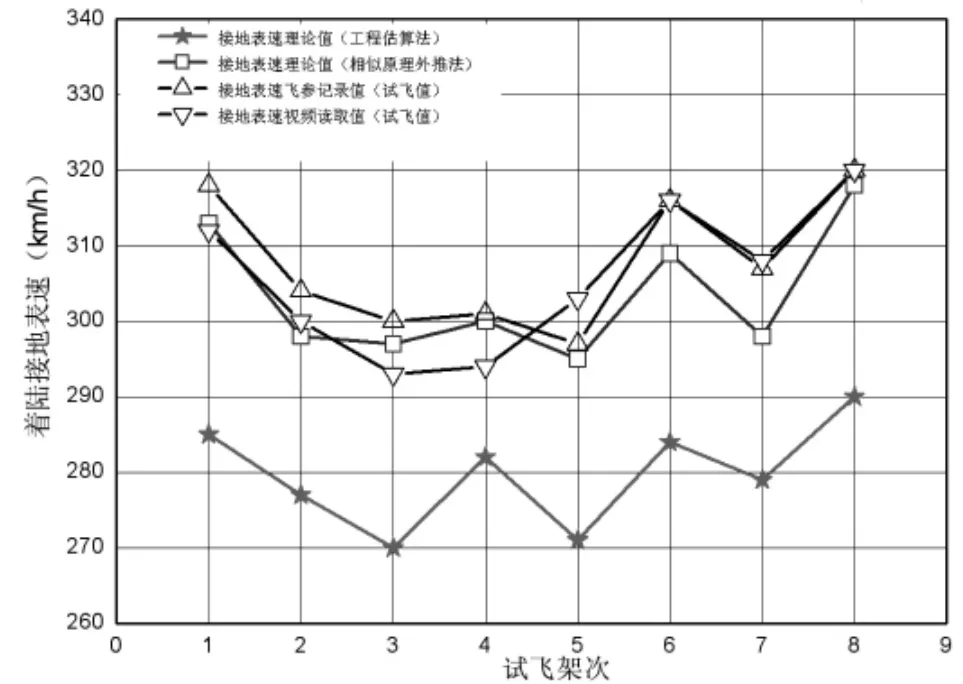
圖4著陸接地表速

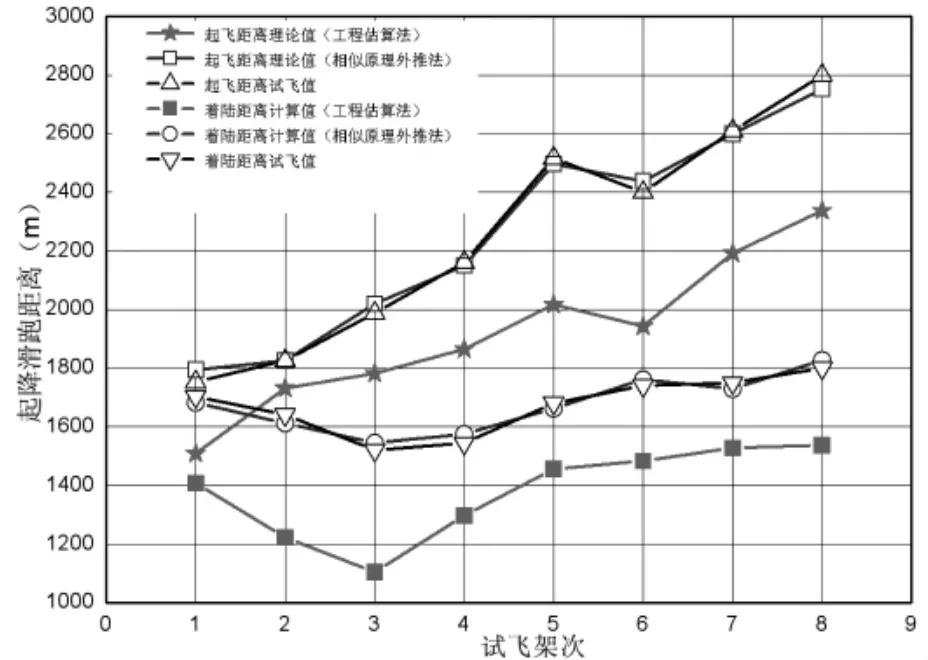
圖5起降滑跑距離

圖3～圖5的結果表明，采用工程估算法獲得的某型飛機起降能力理論值普遍比實際試飛值要小，且兩者誤差多數均達到10%；采用“相似原理”外推法得出的結果與試飛值之間吻合度很好，起飛離地表速計算值與視頻讀取值、飛參記錄值相對誤差大多都在1%以內，個別試飛架次相對誤差最大不超過3.5%；著陸接地表速計算值與視頻讀取值、飛參記錄值相對誤差大多都在2%以內，個別架次相對誤差最大不超過3%；起飛著陸滑跑距離的計算值與試飛值的相對誤差大多在2%以內，個別試飛架次相對誤差最大不超過2.3%。

5 結語

本文提出了一種適用于評估飛機高原起降能力的方法，突破了在缺少非標大氣條件下的發動機推力、油耗數據情況下，無法評估在海拔達到2000米以上高原飛機起降能力的關鍵技術。目前，該方法已成功應用于某型飛機高高原適應性試驗試飛任務中，通過多架次、多構形高原試飛驗證，充分證明了本方法的可行性。

針對高原機場條件惡劣、風險性大、需突破的技術瓶頸多的特點，還提出了一種高高原適應性試飛方法，并結合預先數據研究、理論推導計算開展試飛，極大的降低了試飛風險。文中提出的技術方法和手段具有一定通用性，可應用于其他中小型特技類/作戰類飛機高原適應性試驗試飛任務中，為后續機型進駐高原執行高原起降、高原執勤和作戰任務積累了試驗試飛經驗，對其他型號飛機高原試驗試飛也具有借鑒作用。