基于Simulink對擴張狀態觀測器的仿真分析
李岷釗

摘? ?要:文章對自抗擾控制技術中的擴張狀態觀測器進行研究,分析了擴張狀態觀測器的數學模型,并據此建立了Maltab/Simulink中的仿真模型,并采用控制變量法,對擴張狀態觀測器控制參數對觀測精度的影響進行了探討,對擴張狀態觀測器的參數調節具有一定的指導意義。
關鍵詞:自抗擾控制;擴張狀態觀測器;參數調節
1? ? 擴張狀態觀測器設計背景
擴張狀態觀測器是整個自抗擾控制技術的核心[1]。它的設計借用了現代控制理論中狀態觀測器的思想,根據“能夠影響系統輸出的擾動,其作用必定會反映在系統的輸出上”這一理論,將能夠影響被控系統輸出的系統內外擾動看作系統的總和擾動,將其擴張為一個新的狀態變量,并通過狀態觀測器與系統原有狀態變量一起反饋到輸入端。控制器可據此在控制量中補償擾動,降低外部擾動對控制系統性能的影響。
2? ? 擴張狀態觀測器理論介紹
對于n階控制的系統如下:
(1)
其中,b為系統的輸入矩陣,u為控制器產生的系統控制量。當函數f未知時,可以通過建立如下狀態觀測器對系統狀態變量xi,i=1,…,n進行估計[2]:
(2)
其中β0i,i=1,…,n為狀態觀測器的增益系數,gi(e),i=1,…,n為滿足條件egi(e)≥0的適當的非線性函數。式(2)中的zi(t)為系統狀態變量的估計值,分別觀測不確定系統中的狀態變量xi,i=1,…,n,即zi(t)→xi(t)。
3? ? 擴張狀態觀測器模型建立
仿真實驗中使用的被控對象具有二階傳遞函數,需要設計三階擴張狀態觀測器對系統的狀態變量進行觀測。被控對象的傳遞函數為:
(3)
據此建立的三階擴張狀態觀測器(ESO)為:
(4)
式(4)中的fal函數為非線性函數,其表達式為:
(5)
4? ? 仿真結果分析
定義擴張狀態觀測器的觀測誤差為ei=zi-xi,i=1,2,3。性能指標,n為采集的數據總量。用于衡量參數變化對擴張狀態觀測器輸出性能的影響。
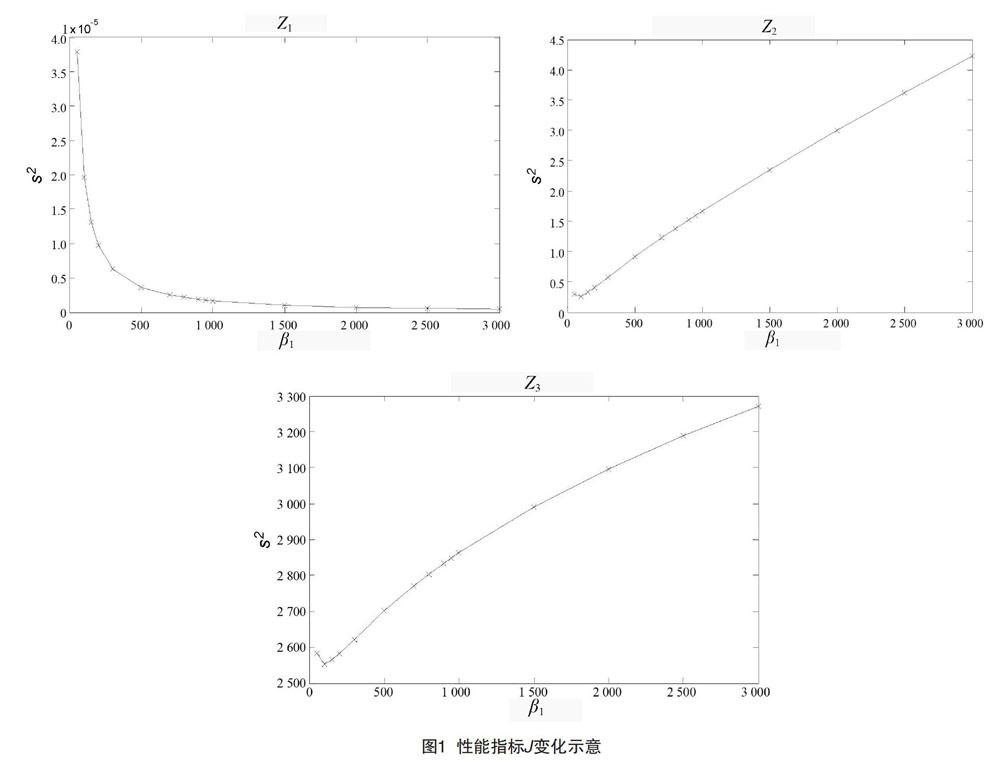
取β2=3 000,β3=10 000,α1=0.5,α2=0.25,δ1=δ2=0.000 1,探究β1變化對擴張狀態觀測器的影響。結果如圖1所示。
由圖1可以得出,提高β1,降低了z2,z3的估計精度而提升了z1的估計精度。
用同樣的方式進行仿真實驗探究β2與β3對擴張狀態觀測器觀測精度的影響,可以得出結論:提高β1,降低了z2,z3的估計精度而提升了z1的估計精度;提高β2提升了z1,z2的估計精度而降低了z3的估計精度;同樣分析可知,提升β3,提升了z1,z2,z3的估計精度。因此,擴張狀態觀測器的參數調節應當按照β1→β2→β3的順序進行。
5? ? 結語
本文通過仿真實驗,得到了擴張狀態觀測器的觀測精度隨其參數變化的影響,擴張狀態觀測器作為自抗擾控制技術的核心,其觀測精度決定著自抗擾控制器的輸出特性。本文得到的結論對自抗擾控制器的調參具有很大的參考價值。
[參考文獻]
[1]黃海燦,韓京清.擴張狀態觀測器用于連續系統辨識[J].控制與決策,1998(4):381-384.
[2]黃一,韓京清.非線性連續二階擴張狀態觀測器的分析與設計[J].科學通報,2000(13):1373-1379.
Simulation analysis of extended state observer based on Simulink
Li Minzhao
(Xian Institute of Electronic Engineering, Xian 710100, China)
Abstract:In this paper, the extended state observer in auto disturbance rejection control is studied, the mathematical model of extended state observer is analyzed, and the simulation model in Maltab/Simulink is established, and the control variable method is used. The influence of the control parameters of the extended state observer on the observation accuracy is discussed, which has certain guiding significance for the parameter adjustment of the extended state observer.
Key words:auto disturbance rejection control; extended state observer; parameter adjustment

