三種用于加工特征識別的神經網絡方法綜述

石葉楠，鄭國磊

北京航空航天大學 機械工程及自動化學院，北京 100083

加工特征自動識別是智能化設計與制造領域中的一項核心技術和關鍵支撐，在所有借助特征進行分析與決策的計算機輔助設計與制造系統中，特征識別均是必不可少的基礎組成單元。在當下的數字化設計與制造中，設計完成的計算機輔助設計(Computer Aided Design, CAD)模型用于計算機輔助制造(Computer Aided Manufacturing, CAM)時，常常存在數據與物理環境間脫節的問題，即物理制造階段僅傳遞面、邊等低級信息，而丟失CAD模型設計中的其他相關信息。計算機輔助工藝規劃(Computer Aided Process Planning, CAPP)從制造需求的角度對CAD模型進行解釋，并重新用“加工特征”來定義，從而解決了CAD和CAM之間的連接問題。

加工特征與加工過程密切相關，涉及加工方式、刀具類型、加工刀軌、夾具等信息。根據加工特征的幾何性質和在CAD模型中的空間關系，通常將其分為獨立特征與相交/復合特征。相交特征由多個獨立的特征組合形成，并在幾何或拓撲結構上發生了改變，其識別是加工特征識別中的難點和重點。現有的加工特征識別方法已得到了廣泛的應用，但是特征識別方法仍然面臨三方面的挑戰：一是特征本身具有多樣性，而不同的應用系統僅根據需要尋求預定特征的識別算法，使得算法不具通用性，無法適應特征多樣性的發展要求；二是特征識別的時間成本較高，特別是在處理復雜特征、相交特征或大型結構件中的多類型特征時，識別時間可能會大幅增加；三是準確率還需進一步提高。

目前針對加工特征識別的方法有很多，其中比較經典的方法可歸納為基于圖的方法[1]、基于體分解的方法[2]、基于規則的方法[3]和基于痕跡的方法[4]。這些方法各有優缺點，但是它們間的共性問題包括：① 不具備學習和抽象能力；② 對CAD輸入模型的抗噪性較差；③ 專注于特定類型的CAD表示，不能推廣到其他不同表示方法的特征表示；④ 處理可變特征、相交特征的能力較差。

恰恰相反，神經網絡方法具有彌補這些共性不足的技術優勢。首先，神經網絡具有學習的能力；其次，神經網絡方法是基于數據驅動的方法，只要建立了一種通用的數學表達方法，就可以統一用神經網絡識別不同類型的特征；再次，神經網絡具有識別相似特征的能力，不需要預定義所有可能的特征實例。因此，自20世紀90年代末開始，國內外學者開始關注和研究利用神經網絡識別加工特征，并取得了一系列顯著的成果[5-6]。神經網絡方法的基本思想是借助神經網絡的學習能力，通過向網絡輸入樣本特征并依據期望輸出結果來反復訓練網絡，以實現特征識別任務。同時，神經網絡的抗噪性能也有助于提高特征識別的準確率。目前，這方面的研究重點在于：① 如何將CAD模型和加工特征轉化為神經網絡的輸入信息，即特征的預處理和編碼；② 選擇何種神經網絡，即神經網絡構架。

神經網絡在計算機視覺與模式識別中的巨大成功已驗證了其強大的識別與分類能力，類比可見神經網絡方法在加工特征識別領域也很有發展潛力。本文針對目前神經網絡在識別加工特征方面的能力和所取得的成果，綜述多層感知機(Multilayer Perceptron, MLP)、自組織神經網絡和卷積神經網絡(Convolutional Neural Network, CNN)三種典型神經網絡的發展現狀，介紹神經網絡識別加工特征的具體方法，包括特征預處理和編碼，以及神經網絡的實現過程，對比分析神經網絡方法與其他特征識別方法及三種神經網絡技術特點，并在此基礎上展望神經網絡識別加工特征技術的發展趨勢。

1 三種神經網絡概述

1.1 多層感知機

感知機是由Rosenblatt[7]最早提出的單層神經網絡，是第一個具有學習能力的數學模型。但是單層的神經網絡無法解決線性不可分問題，而隨后出現的MLP卻解決了這一問題。與單層感知機相比，MLP具有3個典型特點：① 輸入層和輸出層之間添加了隱藏層，且可以為多層；② 輸出層的神經元個數可大于1個，一般情況下，用于預測和函數逼近的MLP的輸出神經元為1個，用于分類的輸出神經元為一個或多個，每一個表示一種類型；③ 隱藏層和輸出層均含有非線性激活函數。

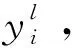
(1)

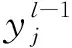
MLP的訓練或學習方式屬于監督型，其主要特點為：對于給定的輸入信息，根據輸出神經元的實際值和期望值之間的誤差來調整隱藏層和輸出層神經元間連接權值，使其最終滿足總體計算誤差要求。常用的訓練方法有多種，例如反向傳播(Backpropagation, BP)法、delta-bar-delta方法、最快下降法、高斯-牛頓法和LM方法等。實驗結果表明，LM方法、高斯-牛頓法和最快下降法等訓練速度優于BP和delta-bar-delta方法，其中LM方法最為有效[8]。

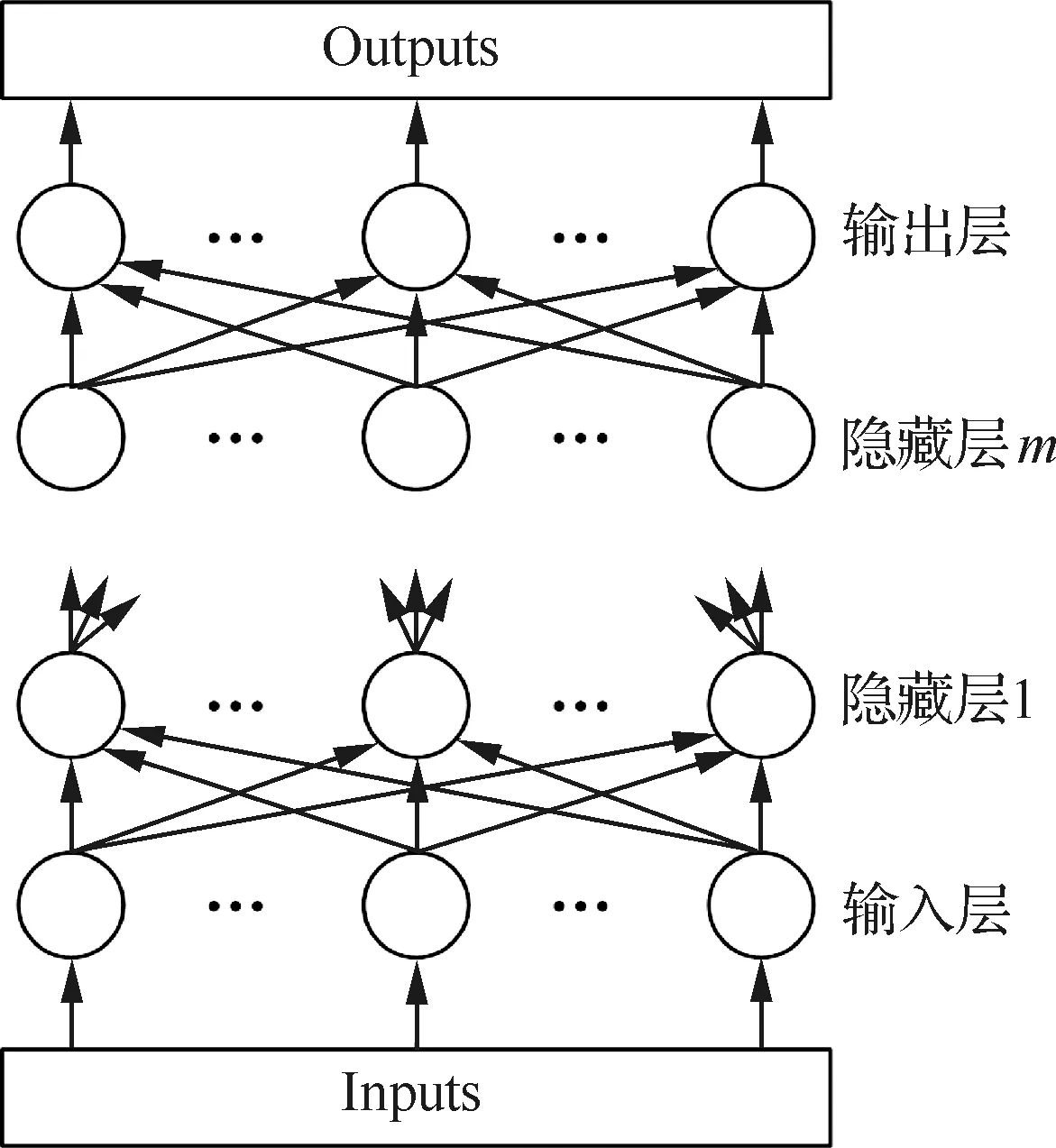
圖1 MLP結構Fig.1 MLP structure

當MLP采用BP方法訓練時，即為BP神經網絡。BP方法是目前最常用的神經網絡訓練方法，其實質是計算誤差函數的最小值問題，按照誤差函數的負梯度方向修改權值。

BP算法包括信號正向計算和誤差反向計算等兩個計算過程。前面所介紹的計算過程即為信號正向計算，而誤差E反向計算式為

(2)

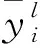
1.2 自組織神經網絡

與MLP類似，自組織神經網絡也是一種前饋神經網絡。但是，自組織神經網絡采用無監督學習方式，具有自組織學習能力，即自動學習輸入數據中的重要特征或找出其內部規律，如分布和聚類等特征，根據這些特征和規律自動調整自身的學習過程，使得之后的輸出與之相適應。對自組織神經網絡來說，學習過程不僅包括網絡參數的調整，也包括網絡拓撲結構的調整。

在加工特征識別領域，已采用的自組織神經網絡有自組織特征映射(Self-Organizing Feature Map, SOFM)和自適應共振理論(Adaptive Resonance Theory, ART)網絡等。

SOFM是Kohonen于1981年提出的一個兩層網絡模型，其中第一層為輸入層，神經元個數與樣本維數相等；第二層為輸出層，也稱為Kohonen層。神經元排布有一維線性、二維平面和三維柵格三種形式，其中最常用的為二維平面形式。SOFM的神經元有兩種連接關系：每個Kohonen層神經元與所有輸入層神經元相連；Kohonen層的神經元之間互相連接，即側向連接，這也是SOFM模仿大腦皮層神經側抑制特性的一個體現。圖2給出了SOFM的3種拓撲結構，其中圓/橢圓表示神經元，實線表示層間連接和輸入/出，虛線表示Kohonen層內神經元間的連接。

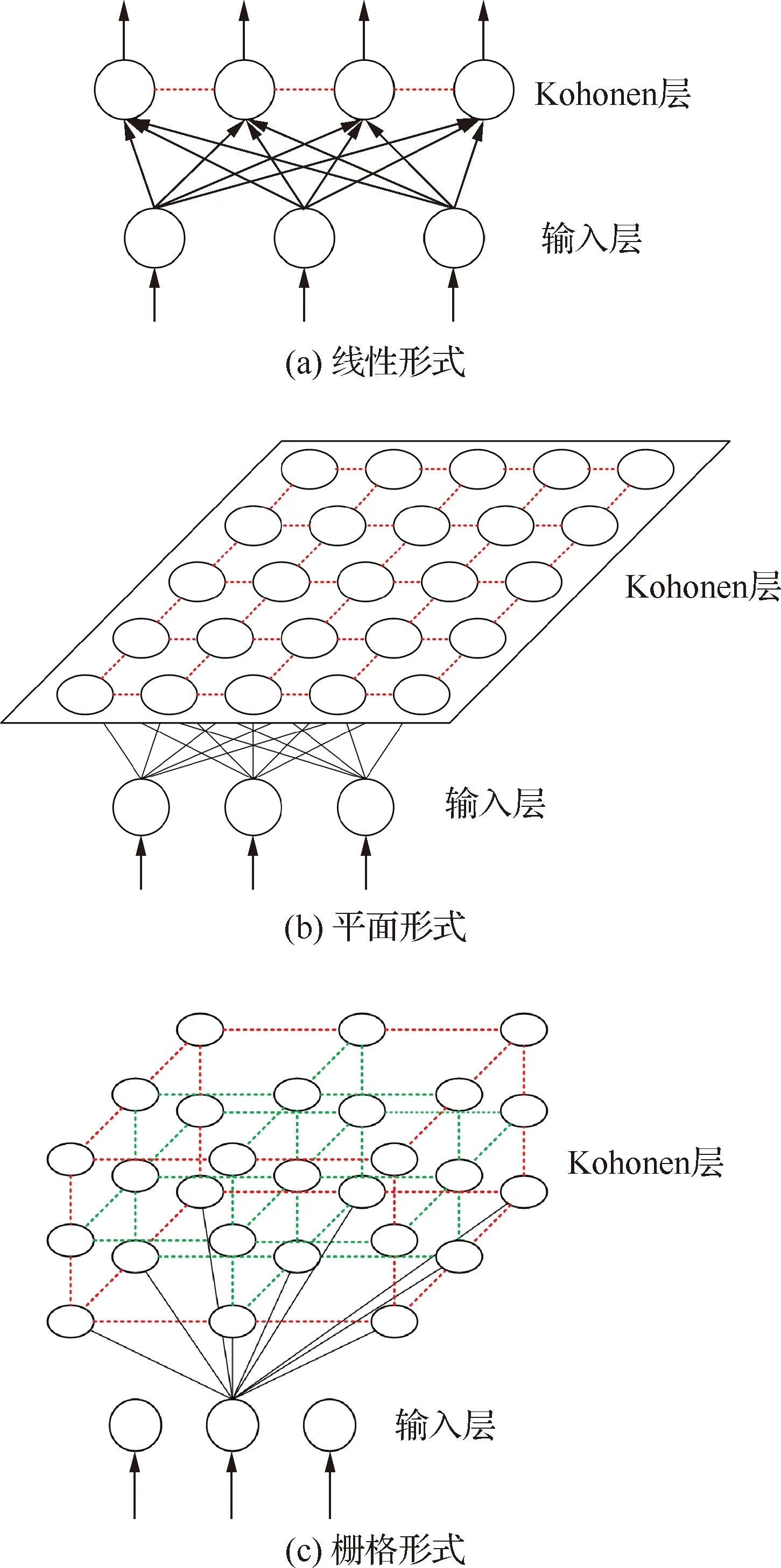
圖2 SOFM拓撲結構Fig.2 Topological structure of SOFM

對于一個給定的輸入，SOFM通過競爭學習得到獲勝神經元，之后獲勝神經元與其附近的神經元(稱為鄰域)一起調整權值，該鄰域特征有助于保持該輸入的拓撲特性。

神經網絡一般具有兩種能力，可塑性是指網絡學習新知識的能力，而穩定性則指神經網絡在學習新知識時要保持對舊知識的記憶。通常，當一個神經網絡對于輸入樣本的訓練學習達到穩定后，如果再加入新的樣本繼續訓練，前面的訓練結果就會受到影響，表現為對舊數據、舊知識的遺忘。ART網絡的建立即是為了解決神經網絡這種可塑性與穩定性的矛盾。

ART理論由Grossberg于1976年提出，隨后Carpenter和Grossberg[9]建立了ART網絡，即ART1。ART1的輸入被限定為二進制信號，使得其應用存在一定的局限性。ART2[10]作為ART1的擴展型，在網絡結構上也進行了一定程度的改進，能夠處理連續型模擬信號。ART1和ART2均為無監督學習類型，具有自組織能力，是ART網絡中的最基本網絡，在此基礎上發展起來了兼容ART1與ART2的ART3、監督型學習的ARTM-AP、基于模糊理論的Fuzzy ART等。用于加工特征識別的ART網絡有ART2和Fuzzy ART。

圖3為ART2的基本構架，由監視子系統和決策子系統兩部分組成。監視子系統包括比較層和識別層(Y層)及兩層間的連接通路。其中比較層包含六個子層，分別為W層、X層、V層、U層、P層和Q層。決策子系統則由R層組成。ART2將相似的特征聚集在一起，特征的相似性則由警戒參數控制。當輸入到網絡的新特征與已存在的特征簇中的成員相似時，新特征就與該簇關聯；否則，ART2為新特征創建一個新的簇。相關變量說明參見文獻[11]。

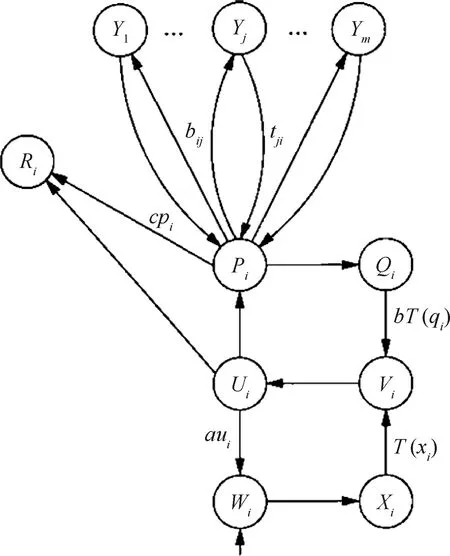
圖3 ART1構架[11]Fig.3 ART1 architecture[11]

1.3 卷積神經網絡

CNN作為目前最著名的深度學習方法之一，已經在圖像識別[12]、場景標記[13]、語音識別[14]、目標檢測[15]、自然語言理解[16]等領域取得了突出的應用效果。CNN在處理和分析大型復雜數據方面具有很強的計算能力，并且由于具有良好的魯棒性，CNN特別適用于視覺相關領域的特征提取和學習任務。

CNN的構架靈感來源于貓視覺皮層簡單細胞和復雜細胞[17]的結構和功能。Fukushima和Miyake[18]建立的Neocognitron可被視為CNN的雛形，其框架由S-layer和C-layer交替組成。早期CNN的代表是LeCun[19-20]的LeNets系列，由卷積層(Convolution Layer, CL)和子采樣層組成(見圖4)。隨著Hinton等[21]在2006年提出layer-wise-layer-greedy-learning方法，深度學習技術才得以真正意義上的建立和發展。2012年，Krizhevsky等[22]使用深度CNN模型AlexNet在ILSVRC ImageNet圖像分類比賽中奪得冠軍后，深度CNN的研究熱潮席卷了整個計算機視覺領域，得到了廣泛的應用[23-26]。

CNN一般由CL、池化層(Pooling Layer, PL)和完全連接層(Fully-connected Layer, FL)組成，CL與PL交替連接，FL多位于網絡最后面。CL由多個特征圖組成，每個特征圖中的神經元都與前一層的神經元鄰域相連，構成CL神經元的感受野，通過權值和激活函數提取感受野的特征。PL的目的是降低CL特征圖的空間分辨率，從而實現對輸入失真和平移的空間不變性，常用方法有平均值池化法和最大值池化法。FL可對網絡中的抽象特征進行解釋，并執行高級推理功能，實現分類和識別目的，常用的算子是softmax算子。CNN的結構決定了CNN有稀疏連接、參數共享和等價表示等三大關鍵要素。

Lin等[27]設計了一種Network in Network模型對CL進行改進，將一個傳統的CL改為多層CL，從而將線性抽象轉變為非線性抽象，提高了CNN的抽象表達能力。Zhai等[28]利用一個雙CL替代單一的CL，用于平衡識別精度與內存占用量(即參數量)之間的關系。雙CL的特點是其元濾波器的尺寸大于有效濾波器的尺寸。計算時，從每個對應的元濾波器中提取有效濾波器，之后將所有提取到的濾波器與輸入連接進行卷積。

對于PL的改進，Krizhevsky等[22]提出了重疊池化方法，即相鄰池化窗口之間存在重疊區域。由于同一個神經元可以參與不同的池化操作，因此可以在一定程度上提高識別結果。為了解決最大池化法容易陷入局部最優的問題，Sermanet等[29]建立了Lp池化方法，該方法可以通過隨機表示將一般球分布擴展到范數表示，并估計最優非線性和子空間的大小。混合池化[30]是一種將平均池化法和最大池化法綜合起來的池化方法，該方法既可以解決最大池化法因參數不均勻造成的失真問題，又可以避免平均池化造成的特征對比度下降的問題，但是該方法的訓練誤差較大。

圖4 LeNet-5構架[20]Fig.4 LeNet-5 architecture[20]

傳統的CNN采用的激活函數多為飽和函數，如sigmoid和tanh函數等。目前，不飽和激活函數成為主流，出現了ReLU[31]及其擴展函數。ReLU是一個分段函數，當x>0時，ReLU(x)=x；當x≤0時，ReLU(x)=0。ReLU的優點是可以幫助神經網絡輕松獲得稀疏表示。LReLU[32]的提出是為了改進ReLU在無監督預處理網絡中的性能，采用的方法是當x≤0時，令LReLU(x)=αx，式中：α為比例因子，是一個給定值。LReLU的變體還包括PReLU[33]，其與LReLU的唯一區別是PReLU的α可以通過BP學習獲得，且沒有額外的過度擬合的風險。

2 神經網絡識別加工特征

2.1 特征預處理與編碼

加工特征存在于CAD實體模型中，包含幾何和拓撲信息，而神經網絡的輸入形式是一組數值信息，也可稱為表示向量(Representation Vector, RV)。因此，如何將CAD模型或加工特征轉化為適用于神經網絡的輸入格式成為了神經網絡識別加工特征的首要問題。本文將該問題表述為特征的預處理與編碼問題。據文獻，神經網絡識別加工特征時，常用的特征預處理與編碼方法主要有：基于屬性鄰接圖(Attributed Adjacency Graph, AAG)編碼、基于面鄰接矩陣(Face Adjacency Matrix, FAM)編碼、基于面值向量(Face Score Vector, FSV)編碼、體素化方法和橫截面分層法等。

2.1.1 基于AAG編碼

加工特征的AAG通常定義為G=N,C,A，式中：N為頂點集，表示特征的組成面集；C為頂點間的連接邊集；A為連接邊的凹凸性集合。AAG只定義了模型的拓撲信息，不含有模型的幾何信息。在基于AAG的編碼中，為了獲得作為神經網絡的輸入RV，需將AAG分解為AAG子圖，再轉化為鄰接矩陣(Adjacency Matrix, AM)，然后根據AM得到RV。

通常，AM是一個二進制的對稱矩陣，以對角線分為凸和凹兩個區域，元素表示行列號所示的兩個面的鄰接邊的凹凸性。取AM的上三角或下三角并按行列號依次排序，所得元素序列即為神經網絡的輸入[34]。

若各AAG子圖的AM規格不一致，可對AM中的元素進一步提煉。首先建立一個有關拓撲與幾何關系的問題表，然后根據AM確定各問題的二進制答案，最后將答案作為RV的各元素值。Nezis和Vosniakos[35]及Guan等[36]均采用該思路創建RV。

2.1.2 基于FAM編碼

基于FAM編碼是基于AAG編碼的改進型，與AM相比，FAM增加了面的編碼信息，因此能夠更加準確地定義面間的鄰接關系。FAM是一個對稱矩陣A=(aij)m×m，其中aii表示第i個特征面的屬性，aij(i≠j)表示第i個特征面與第j個特征面間的鄰接關系，每種關系對應不同的整數值。FAM生成RV的方式與AM生成RV的方式相同。

Prabhakar和Henderson[37]建立了一個8×8的FAM，每一行/列定義為一個含有八個元素的整數向量，分別表示某個面與其鄰接面間的屬性，包括邊類型、面類型、面角度類型、環個數等。該方法的缺點是不能分離拓撲相同但形狀不同的特征。胡小平等[38]在添加虛構面的基礎上設計了一個6×6的擴展型面鄰接矩陣，以虛構的盒形體統一定義特征的表達式，并利用特征面的屬性來區分特征的真實存在面和虛構面，避免特征的描述混淆。

考慮到AAG僅能識別平面和簡單曲面特征，不能處理有共同底面的相交特征，Ding和Yue[39]建立了F-鄰接矩陣和V-鄰接矩陣。該方法通過一個空間虛擬實體(Spatial Virtual Entity, SVE)來表示初始模型生成最終特征時所需移除的實體。兩種矩陣的實例如圖5[40]和圖6[40]所示。其中，F-鄰接矩陣定義特征的組成面類型和面間的夾角，V-鄰接矩陣定義SVE中虛擬面間的關系，即行列號對應的兩個虛擬面是否相連。

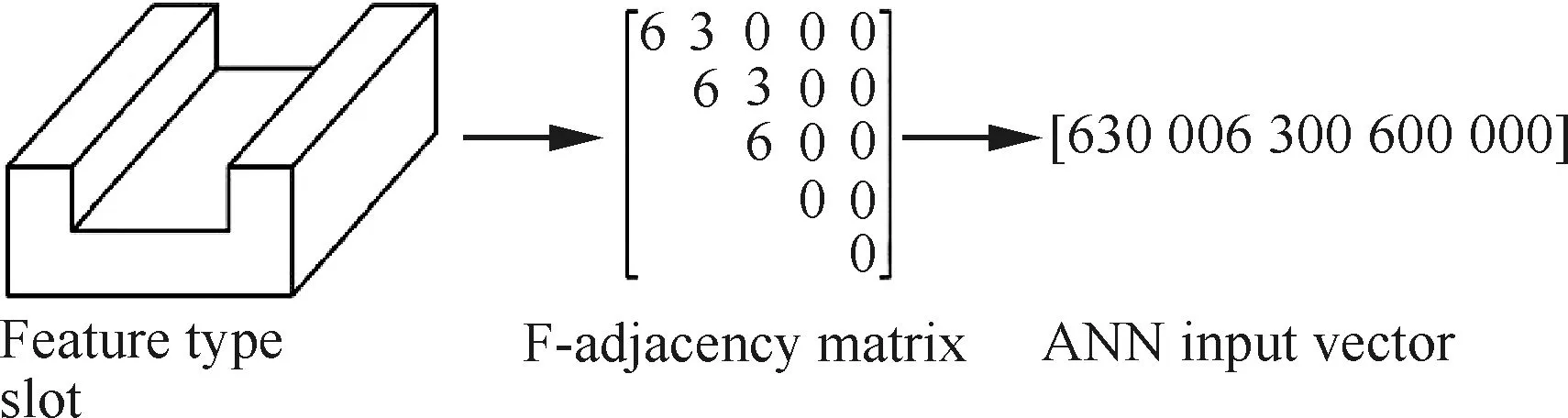
圖5 F-鄰接矩陣實例[40]Fig.5 Example of F-adjacency matrix[40]

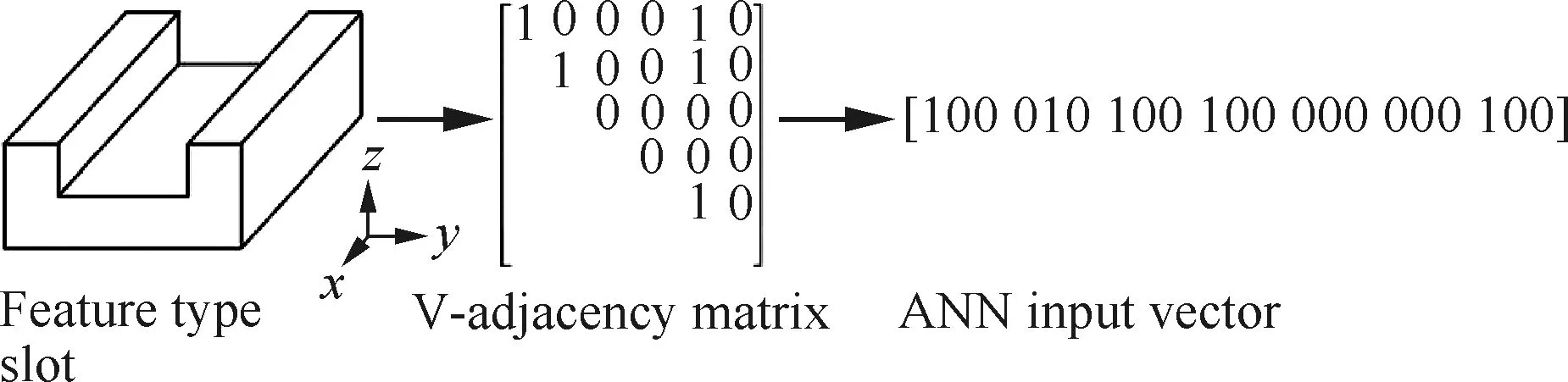
圖6 V-鄰接矩陣實例[40]Fig.6 Example of V-adjacency matrix[40]

2.1.3 基于FSV編碼

面值計算公式是一個與面、邊、頂點特征及其鄰接關系有關的函數[41]，用FSV對特征進行編碼的常用思路為：① 定義FSV的計算式及各分量的分值表；② 定義RV的元素個數和相應的面順序；③ 根據公式計算各特征面的值；④ 將各面值作為元素值生成RV。

FSV的計算公式可概括為F=G′+L+E′+V，F為面分值；G′為面幾何分值，表示面的凹凸性；L為環值；E′為邊值；V為頂點值。通過對相關文獻的研究，該公式有以下幾種表現形式：

1)F=G′+L+V型

該類型的FSV包含面幾何分值、環值和頂點值等三個參數，其中面幾何分值與環值由分值表查詢獲得，頂點值則與過該點的邊值有關。相關實例包括文獻[42-44]等。

2)F=G′+V型

該類型的FSV包含僅包含面幾何分值與頂點值兩個參數。Marquez等[45]采用該公式定義FSV，并用數值的正負表示面、邊等元素的凹凸性。Sunil和Pande[46]采用該方法計算面分值，并將特征的7個組成面的面分值作為輸入RV的前7個元素值。

3)F=G′+E′+V型

?ztürk和?ztürk[47-48]采用該公式將特征定義為一個關于點、邊和面的輸入矢量，這種方法的局限性是僅能表示有限的復合特征，并且特征樣本和特征之間不含一一對應的關系。

4)F=G′+L+E′+V型

Jian等[49]建立的面值計算公式為

(3)

式中：Ai為特征面的分值；Fi為面的權值，定義面的凹凸性；Eij為環的權值；Lik為邊的權值；Vix為鄰接關系權值，定義特征面與鄰接面的夾角關系，其目的是幫助識別V型槽等具有特殊夾角的特征；m′、n′和q分別為相應的對象個數。

2.1.4 體素化方法

體素化方法是三維CNN特有的特征預處理與編碼方法，通過將CAD模型劃分為體素網格，對體素進行二進制賦值，進而獲得CNN的輸入數據。以圖7為例[50]，若體素位于模型內部則賦值1，即綠色點集，若體素位于模型外部則賦值0，即紅色點集。通過這種方法，整個模型可以表示為一長串二進制數字，便于CNN進行卷積計算。

圖7 CAD體素模型的可視化[50]Fig.7 Visualization of voxelized CAD models[50]

體素化的方式包括渲染法[51]和奇偶計數法與射線穿透法相結合的方法[52]。為了加速體素化過程，Balu等[50]利用圖形處理單元劃分體素網格，比CPU方法快10倍以上，而且能夠創建超過10億個體素的CAD體素模型。為了減少特征邊界信息的丟失，Ghadai等[51]利用面法線嵌入網格的方式來增強體素化過程。

2.1.5 橫截面分層法

橫截面分層法[53-54]是指對于具有相同厚度和公共底面的相交特征，采用分層方法得到實體模型的二維合成區域，從而將三維特征屬性轉為二維特征屬性，合成區域的各頂點信息即為神經網絡(如SOFM)的輸入。

圖8給出了一個由實體模型(見圖8(a))生成合成區域的具體過程，在模型的頂點處逐層切片，獲得一系列相互平行的橫截面圖(見圖8(b))后，利用橫截面間的減法處理得到合成區域(見圖8(c))。相關變量說明參見文獻[53]。

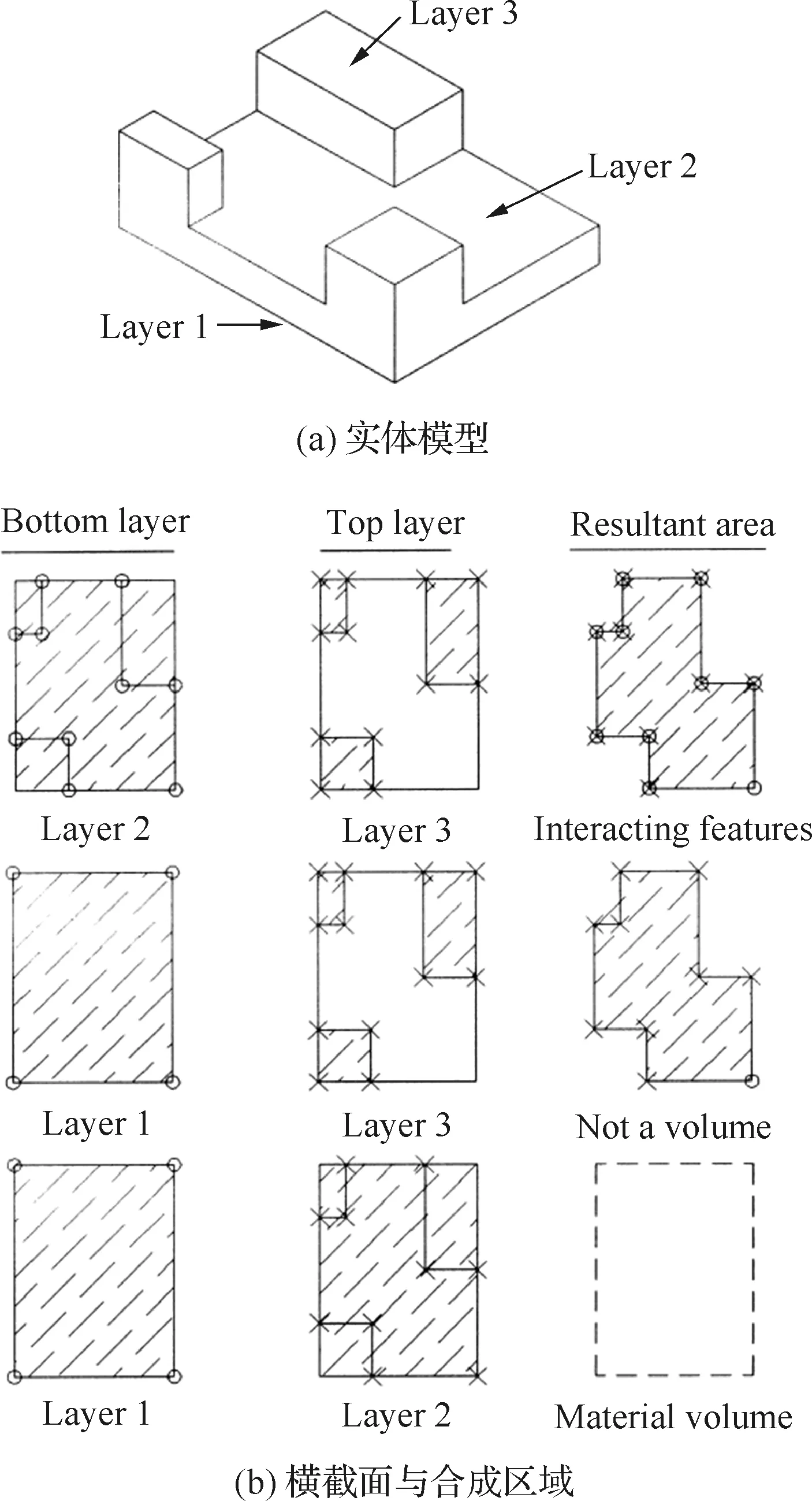
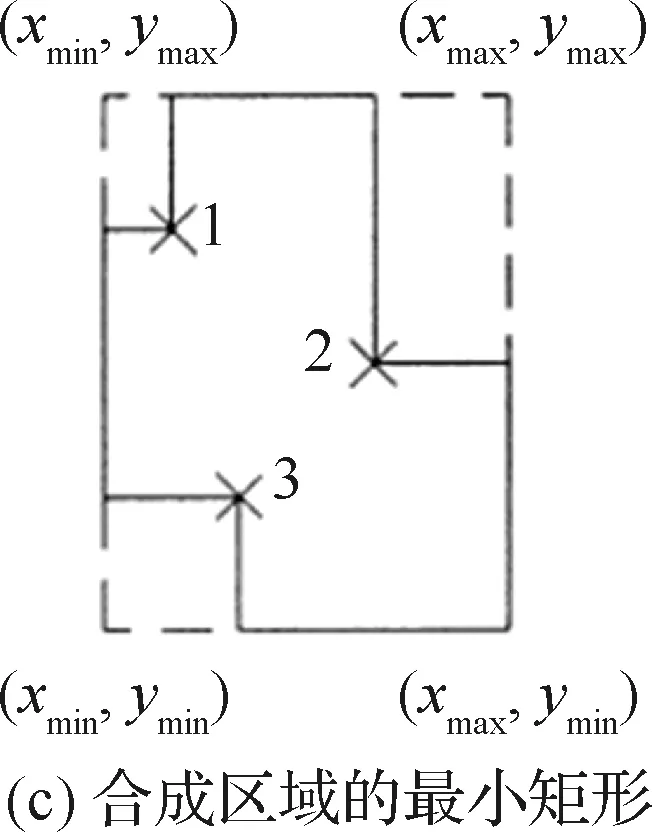
圖8 相交特征的分層方法[53]Fig.8 Layering technique used to find interacting features[53]

2.2 神經網絡結構

神經網絡創建包括三方面的設計：網絡參數設計、數據集構建和訓練方法選擇。面向加工特征識別任務時，神經網絡的數據集為CAD實體模型，網絡參數和訓練方法則根據識別對象的復雜程度和特點進行配置與設計。

2.2.1 網絡參數設計

MLP參數設計主要包括層數選擇以及層的結構設計。雖然目前并沒有明確的設計準則來輔助結構參數的設計與選擇，但是有學者研究發現對于MLP，三層結構足以解決一般性的非線性映射問題，并且能夠滿足要求的準確度[55]。

隱藏層是MLP的設計難點，隱藏層神經元的數量過多會使數據過擬合，造成網絡泛化能力的松散；隱藏層神經元個數較少則會影響網絡的學習能力。比較保守的方法是將隱藏層神經元個數介于輸出神經元數量和輸入神經元數量之間。

表1和表2分別列舉了加工特征識別常用的兩種MLP網絡結構，即三層MLP和四層MLP。其中三層MLP各層的神經元個數分別為n1-p1-q1，四層MLP各層的神經元個數為n1-p1-p2-q1，表中的參數個數是指對一個樣本執行前饋計算時的計算參數量。通過兩表可得以下規律：① 對于三層MLP，p1與n1無絕對的大小關系，通常p1∈[n1,2n1]；② 四層MLP中，一般選擇p1=p2，其目的是簡化神經網絡計算；③ 對比文獻[56]和文獻[47]可知，在n1與q1基本保持不變的情況下，將一個隱藏層分解為兩個隱藏層可以顯著減少參數個數；④ 三層MLP的時間復雜性可表示為O(n1p1+p1q1+p1+q1)，分別改變n1和p1時，時間復雜度的變化分別為O(Δn1p1)和O(Δp1(n1+q1+1))，顯然隱藏層神經元個數的變化對時間復雜度的影響較大。

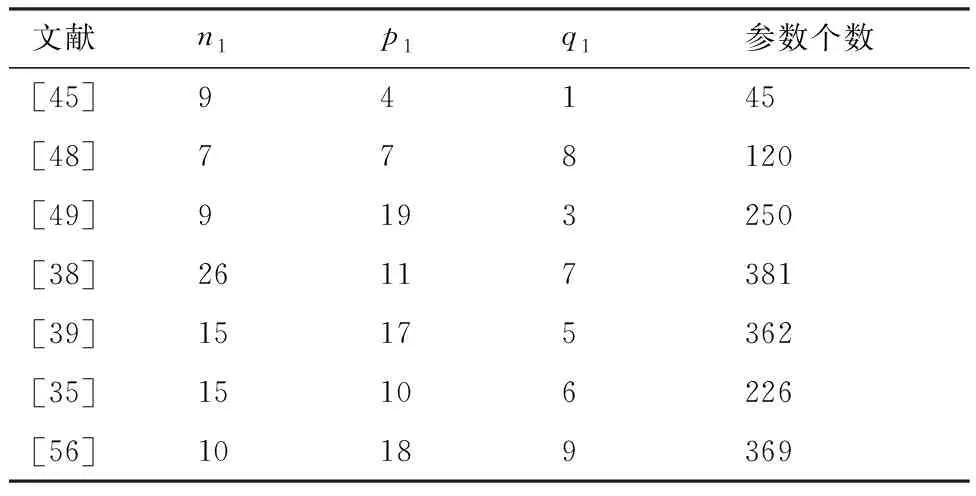
表1 三層神經網絡構造Table 1 Three-layer neural network configuration

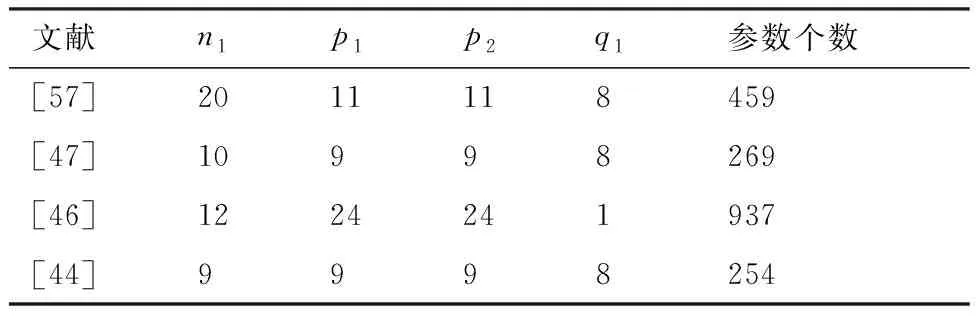
表2 四層神經網絡構造Table 2 Four-layer neural network configuration

SOFM網絡設計主要包括神經元的個數設置和鄰域的尺寸設計。為了識別九種加工特征，Onwubolu[43]建立了一個輸入層有10個節點，Kohonen層有100×100個節點的SOFM，鄰域大小為5。結果顯示，SOFM迭代后可以識別不同類別的特征，且槽和臺階兩種特征被聚為一類。文獻[53-54]將多級SOFM用于相交特征中相交區域的分解，每一級的輸入都是當前合成區域的各頂點，輸出均為2×2數組。

CNN的結構設計包括各類型層的選擇以及過濾器的尺寸設置。其中，常見的類型層包括CL、PL、FL和輸出層(Output Layer, OL)等。為了確定鉆孔特征的可加工性，Balu等[50]建立了一個7層的三維CNN，如圖9所示，依次包括輸入層→CL(8×8)→PL→CL(4×4)→PL→FL(10)→OL(2)。OL的2個神經元分別表示可加工和不可加工。Ghadai等[51]對上述模型進一步修正，在CL和PL后添加了一個批量標準化層，目的是改善網絡的飽和現象進而提高實驗精度。

FeatureNet[52]是第一個將深度學習應用于加工特征識別的三維CNN。FeatureNet的結構如圖10所示，包括4個CL、1個PL、1個FL和1個OL。多個CL的連接有助于對復雜的結構特征分層編碼和識別。OL含有24個神經元，每個神經元代表一種特征。整個網絡擁有3 400萬個參數，遠遠超過MLP的參數量。相關變量說明參見文獻[52]。

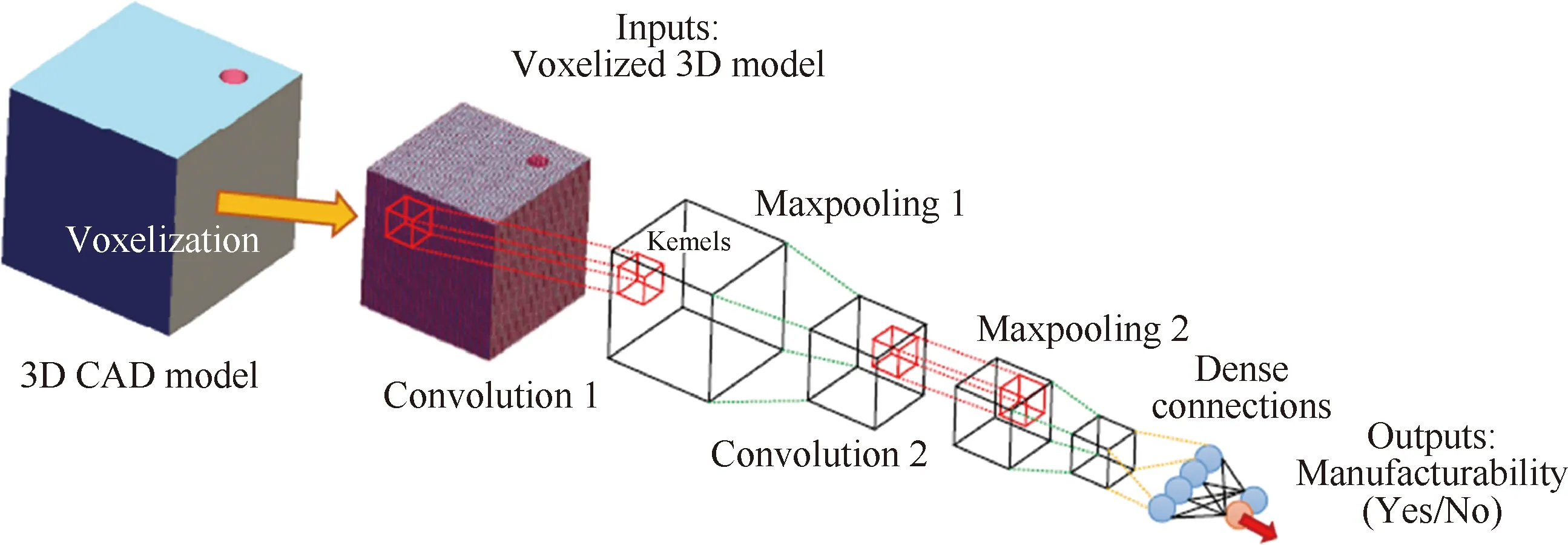
圖9 三維CNN[50]Fig.9 3D CNN[50]

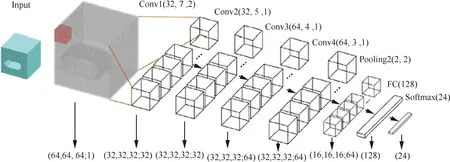
圖10 FeatureNet結構[52]Fig.10 FeatureNet structure[52]

2.2.2 數據集構建

前文提到的三種神經網絡中，MLP和CNN屬于監督型網絡，自組織神經網絡為無監督網絡。監督型神經網絡需要依賴有標簽的數據進行訓練，借助標簽數據的期望輸出來修正權值，調整特征。這種微調建立在大量標簽數據的基礎上，而未標注數據對監督型訓練的作用不大。但是，神經網絡很難獲得足夠多的標簽數據來擬合一個復雜模型，因此標簽數據的獲取是神經網絡訓練的一個難點。創建數據集和遷移學習是數據獲取和擴容的常用方法。

根據文獻，加工特征數據集由一系列CAD 3D模型組成，每個模型一般僅包含一個加工特征，同一類型的加工特征在形狀、位置和尺寸(如半徑、高度、長度等)等方面有所區別，數據集實體模型的類型與神經網絡待識別的特征類型相對應。圖11為文獻[36]創建的訓練樣本，每一類樣本都有各自的輸入矢量與期望輸出矢量，元素均用二進制數字表示。相關變量說明參見文獻[36]。

一個完整的數據集應包括訓練集、測試集和驗證集三部分。其中，驗證集用于調整網絡超參數，不參與最終測試。Ding和Yue[39]建立了一個分層的神經網絡系統，將137個訓練實例和15個測試實例用于第一級網絡后，又將62個訓練實例用于專門識別槽/臺階面的神經網絡，并用12個模型樣本進行測試。Sunil和Pande[46]選擇了95個實例模型用于訓練，20個實例模型用于測試。

與MLP相比，CNN的參數量成數量級倍增加，因此需要規模更大的數據集。Balu等[50]為CNN建立了6 669個正方體模型，每個模型僅包含一個鉆孔特征，且孔的直徑、深度、位置等在規定范圍內變化。模型尺寸均為5英寸。50%的模型作為訓練實例，25%的模型作為驗證實例，其余的作為測試實例。Zhang等[52]為CNN建立了一個更大規模的數據庫，存儲了24種特征(見圖12)，每種特征含有6 000個不同的樣本模型。這些模型均為統一規格(10 cm)的正方體結構。

圖11 訓練樣本的輸入與輸出[36]Fig.11 Input and output of training samples[36]

隨著深度CNN的迅速發展，大型數據集對CNN的影響和作用越來越明顯，更加凸顯了數據集創建的必要性。對于一些很難獲得的標簽樣本，遷移學習是數據集擴充的一種有效方法。遷移學習是一種運用已有知識對不同但相關領域問題進行求解的機器學習能力，常用的一種方法是對預訓練模型進行微調。例如，Shin等[58]對AlexNet和GoogLeNet微調時，將CNN所有層(不含最后一層)的學習速率由默認值減小了10倍。Han等[59]仔細研究了預訓練網絡的超參數調整，利用貝葉斯優化來處理學習率的搜索問題。

圖12 24種加工特征[52]Fig.12 24 manufacturing features[52]

2.2.3 訓練方法選擇

神經網絡最常用的訓練方法為BP算法，文獻[10,19,46]等均采用此方法。然而，該方法存在一定的局限性，收斂速度慢和容易陷入局部極小是其中的兩大問題。目前針對BP算法的改進措施中，動量法是較常用的一種方法。通過在原來的權值調整公式中增加一個含動量比的乘積項，能夠減小學習過程中的振蕩趨勢，降低網絡對誤差曲面局部細節的敏感性，從而改善收斂性，抑制網絡陷入局部極小。

Ding和Yue[39]采用了共軛梯度算法訓練神經網絡，該方法在一組相互共軛的方向調整權值，與最快梯度方向相比能獲得更快地收斂。Shao等[60]選擇粒子群算法訓練MLP，初始化一群“粒子”后通過迭代尋找最優解，迭代過程中不斷更新粒子本身的最優解和全局最優解。該方法的優點是收斂快，精度高。Jian等[49]設計了一種新型蝙蝠算法(Novel Bat Algorithm, NBA)訓練BP神經網絡，與粒子群算法相比，該方法能夠控制局部搜索與全局搜索之間的轉換，避免網絡陷入局部最優缺陷，有助于提高特征識別的準確性。

警戒參數ρ是ART2計算過程中的一個重要參數。ART2將相似的特征聚集在一起，特征的相似性則由警戒參數控制。當網絡新輸入的特征與特征簇中的已有成員相似時，新特征就與該簇關聯；否則，ART2為新特征創建一個新的簇。一般情況下，隨著警戒參數的提高，ART2的聚類由粗糙轉向精細化，這種現象在Fuzzy ART[61]中也得到了驗證。隨著警戒參數ρ依次選擇為0.85、0.95、0.98和0.99，五種特征由共享一個簇發展為擁有各自的簇(見圖13)。

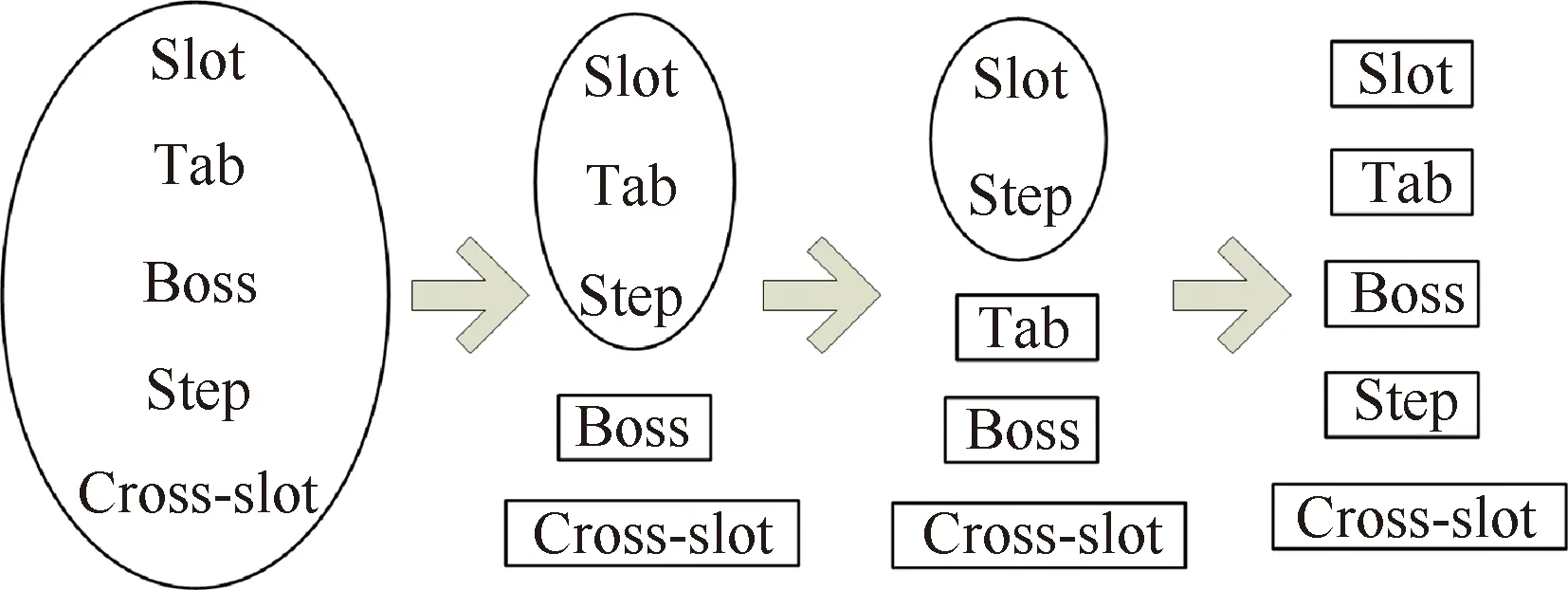
圖13 Fuzzy ART分類Fig.13 Fuzzy ART classification

3 對比分析

3.1 神經網絡方法與傳統方法

近30年來，有關加工特征識別的研究已經相當成熟，并形成了多種不同類型的識別方法，每種方法都有各自的優勢和不足。

基于圖的方法具有特征定義簡單，算法效率高，能準確描述特征面鄰接屬性等優點，但是該方法識別相交特征時易丟失鄰接關系。基于體分解的方法不受特征拓撲結構的限制，能夠較好地處理相交特征的識別，然而識別過程依賴大量的布爾運算，導致計算量大、算法效率低下。基于規則的方法在特征表示方面具有很好的性能，但是對每種特征都進行規則預定義是不現實的，故該方法靈活性較低。此外，拓撲或幾何變形可能會使簡單特征的規則描述過于繁瑣，造成計算成本較高[62]。基于痕跡的方法多以幾何與拓撲信息作為痕跡進行識別，當痕跡指向多種特征時，需要進一步的幾何推理來獲得所需特征。該方法雖然可以有效地識別相交特征，但是當痕跡的數量明顯多于特征時，可能會導致無效的特征或特征被其他特征所覆蓋[63]。

與這些主流的識別方法相比，神經網絡識別方法具有以下幾點優勢：① 具有學習能力[64]，能夠隱式推導特征的構造關系，識別和分類具有不同尺寸和拓撲的相似特征；② 具有泛化能力，通過訓練可以識別預定義的一組特征，進而可擴展到識別新的特征；③ 訓練完成后可保持很高的處理速度；④ 抗噪性能好，有利于識別相交特征。

然而，神經網絡方法識別加工特征仍然存在著一些不足：① 神經網絡輸出層的神經元個數一般為待識別的特征類型數，但是中間各層的結構配置方法還需進一步研究；② 加工特征數據集的樣本模型結構簡單，只包含一個特征，且多為標準特征，不含有相交特征；③ 加工特征識別前需要將其轉換為數值表示，轉換過程中容易造成特征某些信息的丟失，影響識別精度。

表3對比了不同特征識別方法的識別范圍。

表3 特征識別方法與識別范圍

Table 3 Feature recognition methods and their recognition range

識別方法識別范圍基于圖獨立特征基于體分解獨立特征,有限個相交特征:僅含柱面和平面基于規則獨立特征,預定義的相交特征基于痕跡尺寸適中的獨立特征,相交特征神經網絡獨立特征,相交特征

3.2 不同神經網絡方法

本節針對三種神經網絡方法，分別從輸入特性、輸出特性、識別范圍和相交特征處理等幾個方面分析各自的特點。

3.2.1 輸入特性

一種合理且有效的特征預處理與編碼方法必須具備三點特性：① 能夠準確且完整地表達加工特征的幾何與拓撲信息；② 能夠被輸入層識別，符合RV的要求；③ 每一類特征都有唯一的表示，各類特征間的表示不重疊。

根據組成元素類型，RV可分為三種：① 整數型，即元素均為整數；② 實數型，即元素均為實數；③ 二進制型，即元素僅有0和1兩種值。通常，基于AAG和FAM編碼的RV多為整數型或二進制型，基于FSV的RV元素多為小數，體素化方法得到的體素網絡均用二進制表示。

表4總結了三種神經網絡常用的特征預處理與編碼方法。由于特征具有復雜的拓撲與幾何特性，因此綜合了面、環、邊和點信息的面編碼方式比AAG編碼方式更準確，也更有效。自組織神經網絡的輸入同樣依賴CAD模型的B-rep信息提取和特征表達方法，因此，能夠更好反映拓撲信息的特征表達方法對提高自組織神經網絡的穩定性和魯棒性具有重要意義。

關于CNN的輸入類型，一方面，CNN的體素化表達是一種與幾何信息無關的數值轉換，而其他兩種神經網絡從B-rep模型提取幾何信息，并借助預定義的公式生成RV；另一方面，CNN直接選擇體素(三維形式)作為輸入，與將三維對象簡單投影到二維表示(如深度圖像或多視圖等)相比，既可減少幾何特征的丟失，又可避免局部或內部特征不易投影的問題。

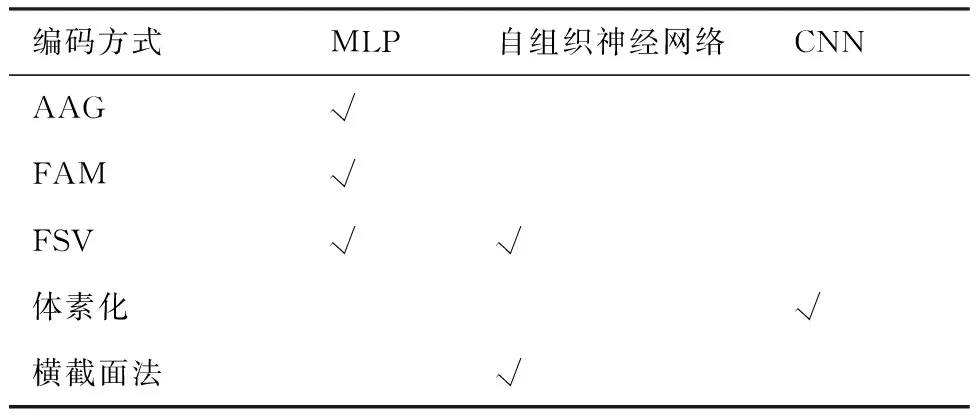
表4 三種神經網絡的常用編碼方法

3.2.2 輸出特性

神經網絡的輸出是神經網絡的輸入與權值反復計算和相互作用的結果，從形式來看，神經網絡的輸出有以下幾種形式：① 單個神經元的輸出；② 向量形式的輸出；③ 矩陣形式的輸出。

文獻[45-46]屬于單個神經元的輸出形式。其中文獻[45]為每一種特征建立了一個三層MLP，其輸出為一個二進制數值，用于表示該類型特征的識別結果。文獻[46]的輸出值是一個實數值，且不同的數值代表不同的識別類型，如 0.10 代表三角形型腔，0.12代表長方形型腔等，所有特征類型的輸出值位于區間[0.1,0.8]。

向量是最常見的神經網絡輸出形式，可分為二進制形式的向量和實數值形式的向量。在二進制型向量中，若每個神經元對應一種類型的加工特征，且每次僅激活一個輸出神經元，則該向量為one-hot向量。文獻[34,36,39]等均采用該輸出方式。文獻[49]雖然也是二進制向量輸出，但是存在兩個神經元同時激活一種特征的情況，如[0,1,1]表示通槽，因此不屬于one-hot向量。實數型向量的代表有文獻[52]等。此外，Hwang和Henderson[41]應用了含六個元素的輸出向量，每個元素分別代表類、名稱、置信因子、主面名稱、關聯面列表以及總執行時間。

矩陣也是神經網絡輸出的一種形式，文獻[53]建立的SOFM的輸出即為一個二進制矩陣O=[bij](i=1,2;j=1,2,3,4,5)，其中b1j代表識別的特征代碼，b2j表示該特征在五個坐標軸方向上的可加工性。

總之，二進制向量形式是最常用的神經網絡輸出形式，若采用one-hot編碼，每次計算僅有一個輸出神經元被激活，因此特征類型數即為輸出向量的元素個數。以3種特征為例，one-hot編碼需要3個輸出神經元，而非one-hot編碼僅需2個神經元，可表示為[0,1]、[1,0]和[1,1]，由此可見one-hot編碼在一定程度上增加了神經網絡的參數量，表1中文獻[49]和文獻[56]的對比也反映了這個問題。

3.2.3 識別范圍

由于神經網絡類型的不同，特征預處理方式的不同，以及訓練方法等的不同，加工特征識別的范圍也不盡相同。本文對相關文獻進行了詳細的分析，并列舉了部分文獻識別加工特征的范圍和優缺點，相關內容見表5，其中I級特征與II級特征的說明見3.2.4節。

由表5可知，槽、臺階、型腔、孔等簡單特征最易識別，相交特征特別是II級相交特征是各種神經網絡識別的難點。近年來隨著研究的深入，相關算法也在進一步發展。遺傳算法、NBA算法等其他技術被應用到MLP中，提高了識別性能，然而識別范圍并沒有明顯的擴展。深度學習技術雖然是加工特征識別的新方法，但在識別范圍和精度方面均有明顯優勢，由此也體現了以CNN為代表的深度學習方法在加工特征識別領域的潛在能力。

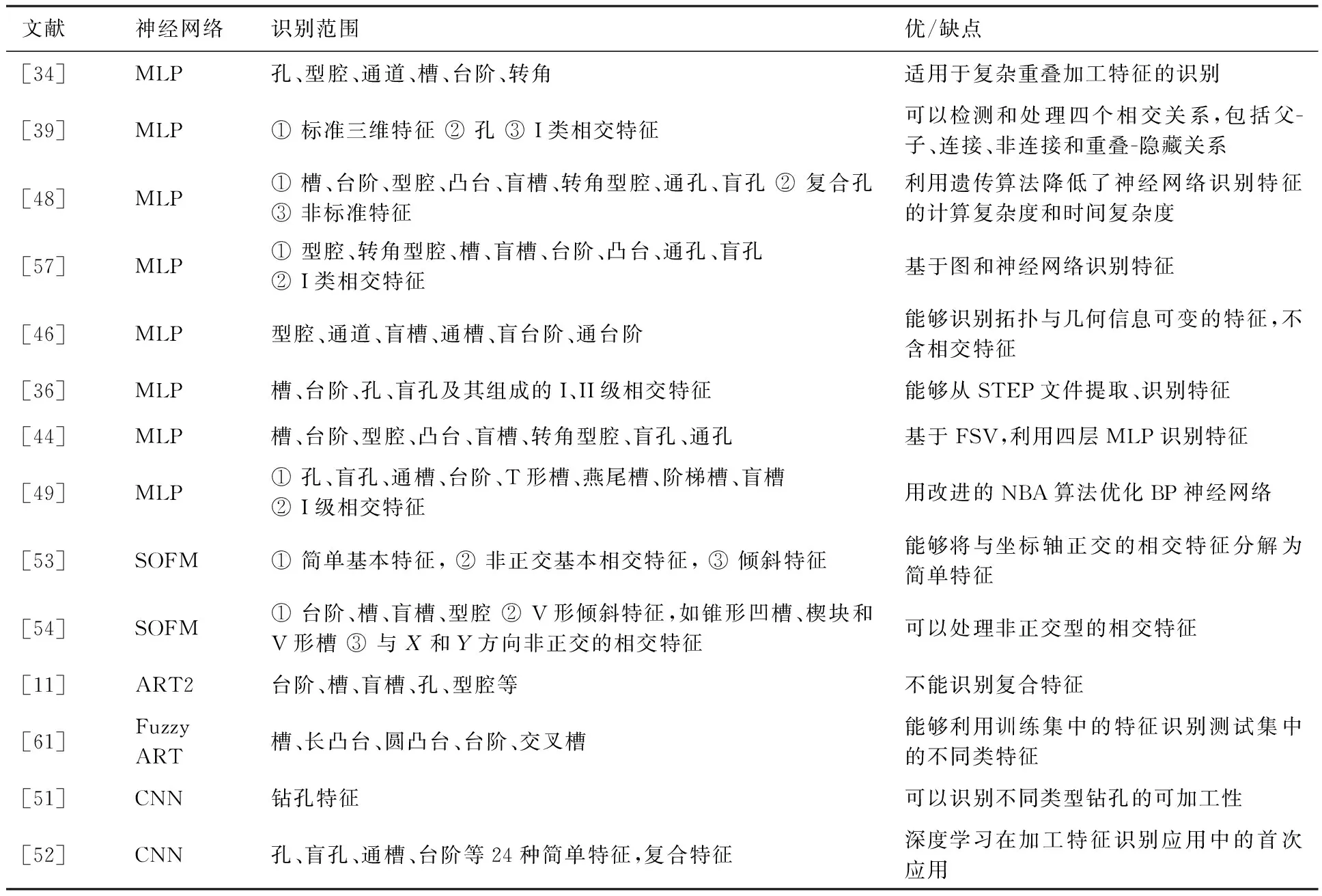
表5 基于神經網絡的特征識別方法Table 5 Feature recognition methods based on neural networks

3.2.4 相交特征處理

相交特征識別一直是特征識別的難點，復合/相交特征存在兩種形式的特征交叉。在第一種形式中，簡單特征的內部面同時是其他簡單特征的外部面，這種復合特征能夠分解出多個完整的簡單特征，可稱為I類相交特征。另一種特征交叉中，兩個或多個簡單特征具有共同的面，且這些面均位于特征的內部，該類型的特征不能分解出相互獨立的子特征，可稱為II類相交特征。神經網絡識別相交特征具有一定的優勢，其主要原因是神經網絡具有良好的抗噪性，當輸入特征為相交特征時，神經網絡通過訓練可在一定程度上學習相交特征的主要特點，忽略次要信息，進而識別得到正確結果。常見的相交特征處理方法可歸結為分解子圖法、啟發式算法、橫截面分層法和基于軟件包的方法等，其中：

1) 分解子圖法

基于AAG和FAM編碼的神經網絡識別復合特征時，通常先生成模型的AAG，然后再用啟發式算法或其他方法生成子圖，每個子圖只包含一個簡單特征，最后將子圖轉為神經網絡的輸入。文獻[36]即用這種方式處理相交特征。

對于一些復合特征，如多級孔等，子圖分解方法可能會將其分為多個子特征。然而，考慮到特征間的相互作用，這些子特征應被識別為一個統一的整體。為了解決此問題，文獻[49]對子圖分解后得到的任意兩個AM(特征因子)進行比較，若存在公共面和公共基面，則將這兩個特征因子組合為一個特征。

2) 啟發式算法

啟發式算法識別相交特征的基礎是利用相交特征對構建不同類型的相交實體(Interacting Entity, IE)。首先遍歷模型中的所有特征，然后對每個特征對執行布爾交叉運算，最后分析IE，從而確定每對特征的關系。具體算法可參見文獻[39]。文獻[35]利用啟發式算法將復合特征分解為簡單特征，之后輸入神經網絡進行識別，但是該方法不能處理II類相交特征。

3) 橫截面分層法

文獻[53-54]識別相交特征時，利用橫截面分層的方法獲取相交區域的頂點，然后用SOFM進行聚類，結合布爾運算分解相交區域和提取體積數據，實現整個相交特征合成區域的分離。根據相交區域的復雜程度，該過程可能需要執行多次SOFM操作。

4) 基于軟件包的方法

FeatureNet[52]使用Python的scikit-image包中提供的連通分量標記算法，先將不相鄰的特征或特征子集彼此分離，再利用分水嶺分割算法將每個分離的特征子集分割為單個特征，最后輸入到CNN進行識別。

4 展 望

神經網絡識別加工特征是同時利用和融合了神經網絡學習特性和CAD/CAM/CAPP專業屬性，是一種完全有別于傳統識別方法的跨學科技術。其可能的發展趨勢如下：

1) 深度學習算法應用。目前，CNN已經被初步應用到加工特征的識別中，但是采用的結構簡單，數據集的規模也較小。未來可以考慮模仿AlexNet、VGGNet等深層網絡結構建立更加復雜的CNN模型識別加工特征。同時，鑒于ImageNet對分類和識別任務的重要性，有必要建立一個種類多樣、模型復雜、尺寸變化大、形狀不規則的CAD模型數據集，為神經網絡訓練和測試提供數據。此外，體素化方法在邊界特征表示、計算效率等方面還不太完善，也需進一步優化和思考。

2) 全信息特征識別。從CAD/CAM/CAPP角度考慮，為了保證下游CAPP模塊或檢查和裝配過程規劃中能夠獲得有效的特征，特征識別系統除了能夠識別形狀特征外，還應找到零件的特征和相應的尺寸及公差之間的匹配關系，具體涉及尺寸、幾何公差、形位公差及其他特征屬性等。因此需要研究神經網絡對多種不同類型屬性的識別問題，以及建立配套的特征表示方法。

3) 類人腦認知結構。神經網絡的本質是基于數據驅動的數值計算方法，因此任何類型的神經網絡識別加工特征都須將CAD模型轉換為數值輸入。神經網絡是對大腦系統的模仿和再現，同樣地，利用類人腦技術模仿大腦的某些機理，也可以建立新型的神經網絡。其中的一種構思是將網絡設計為與傳統神經網絡類似的結構形式；在輸入類型上直接以面作為輸入，不必轉換為數值信息；神經元處理函數不再是數值型的激活函數，而是自定義的認知表達式形式。此時的神經網絡可轉變成一種基于邏輯運算的神經網絡。這也是神經網絡在3D模型的面特征識別領域的一個發展方向。

5 結 論

本文針對智能化設計與制造領域中的加工特征識別這一關鍵技術問題，介紹了近年來興起的新型識別方法，即神經網絡識別方法。根據目前的研究現狀和主要采用的神經網絡類型，將特征識別分為三種不同方法，并進行了較為全面的論述和分析。

1) 系統性地論述了MLP、自組織神經網絡和CNN等三種不同神經網絡的原理，詳細研究了神經網絡在加工特征識別領域的計算方法。

2) 進一步歸納了神經網絡方法采用的特征預處理方式和網絡結構，深入分析了每種神經網絡的特性和優缺點。

3) 總結了目前神經網絡識別加工特征的優勢，指出了其中存在的一些問題和面臨的挑戰，并展望了該領域未來的發展方向。