考慮測試性設計缺陷修正延時的測試性增長模型建模與評價方法

李天梅，司小勝，楊宗浩，徐從啟，張琪

1.火箭軍工程大學 導彈工程學院，西安 710025 2.火箭軍士官學校，青州 262500 3.中國人民解放軍32181部隊，西安 710032

測試性增長模型(Testability Growth Model，TGM)是跟蹤并預計裝備測試性水平增長過程的數學模型，是裝備測試性增長分析過程的核心要素。而為了更加方便有效地實現測試性增長跟蹤與預計，需要建立測試性增長參數化學習曲線時間函數模型[1-2]。

近年來，測試性增長建模相關問題已成為測試性工程領域的熱難點問題。Li等[3]研究建立了測試性增長參數化學習曲線時間函數模型，該模型通過分析測試性設計缺陷(Testability Design Limitation，TDL)變化規律，構建具有鈴形變化規律的測試性增長效能函數來表征已識別TDL數量變化趨勢，并假設TDL在識別后立即被修正，不存在時間延遲，且不引入新的TDL。Zhao等[4-5]針對試驗過程中故障模式可能發生變化的情況，并假設對識別的TDL不能一次性根除，分析測試性指標變化規律，提出了一種基于馬爾科夫鏈考慮非理想修正的測試性增長參數模型。該模型是以單個故障模式不可檢測/隔離概率作為馬爾科夫鏈的狀態轉移概率，但對于大型復雜裝備，每個故障模式的不可檢測/隔離概率數據很難獲取，且所獲取數據具有很大的不確定性，因此影響所建立測試性增長參數模型的準確性。

以上模型的提出對測試性增長試驗的開展具有重要理論指導意義，但這些模型忽略了測試性設計者的學習過程和TDL修正延時問題。測試性設計者學習過程是指隨著裝備測試性增長過程的進行，測試性設計人員對系統越來越了解，對測試性設計技術越來越熟悉，對TDL修正能力越來越強。修正延時是指TDL修正過程滯后于TDL識別過程的現象，從時間角度來看就是TDL被識別之后到完全被修正所需要的那一段時間。因此，如何考慮測試性設計者的學習過程和修正延時現象建立準確的測試性增長參數化學習曲線時間函數模型十分必要。

在軟件可靠性領域中，有大量考慮故障修正延時的軟件可靠性增長模型。Schneidewind[6]首先提出故障修正過程是影響可靠性和測試進度的主要過程，他從時間角度分析了故障修正延遲現象，并在假設修正延遲是一個常數的基礎上建立了故障修正過程的軟件可靠性增長模型。在此基礎上，一些學者還提出了基于不同時間延時函數的軟件可靠性增長模型[7-9]。在測試性增長過程中，修正TDL是測試性設計增長的主要目的，對于不同的TDL其修正的難易程度不同，需要的修正時間不同，同時，隨著測試性設計者學習過程的存在，很難用一種時間延時函數統一描述。然而與描述每個TDL的延時時間相比，測定已識別TDL數量和已修正TDL數量是較為簡單的和可行的。事實上，測試性增長的目的就是逐一識別并修正TDL，這里將已經識別到但未修正的測試性設計缺陷，稱為剩余測試性設計缺陷(Remaining Testability Design Limitation，RTDL)，RTDL數量能直接反映測試性設計水平的高低。

基于以上分析，本文考慮測試性設計者的學習過程，在分析TDL識別過程與修正過程存在延時關系的基礎上，通過分析TDL識別與修正機理及變化規律，構建具有鈴形變化規律的剩余測試性設計缺陷函數，在此基礎上，研究建立基于Gamma、Rayleigh和Delay-S 3種鈴型曲線考慮修正延時的測試性增長參數化學習曲線時間函數模型；最后，基于某機載穩定跟蹤平臺的增長試驗數據，驗證所提測試性增長模型的有效性。

1 RTDL變化趨勢分析

在實際的測試性增長試驗中，TDL必須在被識別之后才能被修正。一般來說識別的測試性缺陷數量越多，修正的TDL也隨之增多。與此同時，修正的TDL數量越多，TDL修正人員積累的經驗也越多，可以更容易對已識別的TDL進行修正。

在測試性增長試驗初期，隨著注入的故障模式數量逐漸增加，TDL逐漸被識別，已識別TDL數量不斷增多。此時，由于設計師缺乏經驗，TDL不容易被修正，所用的修正時間較長，TDL修正效率較低，TDL的修正過程將滯后于TDL的識別過程，RTDL不斷增大。隨著測試性增長試驗的進行，在規定的故障注入次數下，能識別的測試性設計缺陷數量逐漸達到飽和，設計師不斷學習，對儀器、工具、方法逐漸掌握，經驗不斷積累，TDL的修正效率不斷提高，RTDL數量逐漸減小，TDL的修正過程逐漸逼近TDL的識別過程。而且RTDL能夠從測試性設計缺陷數量上直接反應修正延時的變化過程，且具有“先增后減”的變化趨勢。

衡量測試性的指標包括故障檢測率(Fault Defection Rate，FDR)、故障隔離率、以及虛警率等，這些指標在數學上沒有相關性。因此一般情況下，一次測試性增長試驗只能以一個測試性指標增長為目標。不失討論問題的一般性，接下來的論文部分以FDR增長模型建模為例展開討論。

2 考慮TDL修正延時的FDR增長模型

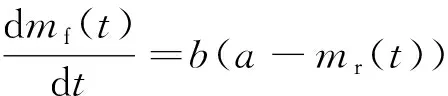
(1)

式中：a為最初隱藏于系統中的TDL數量；b為比例系數，不失討論問題的一般性，假設b為常數；mf(t)為識別出的TDL數量；mr(t)為識別并有效修正的TDL數量。

由第1節分析可知，由于存在測試性設計者的學習過程，導致TDL在識別出來后不能被立即修正，即存在TDL的修正延時問題。RTDL數量記為y(t)，即

mf(t)-mr(t)=y(t)

(2)

將式(2)代入式(1)可得

(3)

FDR的數學模型可表示為

(4)

式中：M為故障模式總數，可以通過故障模式影響及危害性分析得到；ND為系統測試性設計能夠成功檢測到的故障模式數量。

ND的表達式為

ND=M-(a-mr(t))

(5)

ND=M-[a-(mf(t)-y(t))]

(6)

將(6)式代入(4)式可得

(7)

式中：q(t)即為考慮TDL修正延時的測試性增長參數化學習曲線時間函數模型的一般表達形式。

由于測試性試驗工程師具有一定的學習能力，隨著測試性增長試驗的開展，RTDL數量具有先增后減的變化趨勢，借鑒軟件可靠性增長領域考慮學習過程的鈴形曲線形式[10-13]，分別采用Gamma、Rayleigh和Delay-S 3種鈴形曲線表示RTDL變化趨勢，將這3種曲線代入式(6)，即可得到考慮TDL修正延時的3種不同曲線特性下的FDR增長模型。

2.1 基于Gamma修正延時曲線的FDR增長模型

Gamma曲線可以表示為[10]

(8)

由式(8)可知，Gamma曲線是一條光滑的鈴形曲線，如圖1所示。

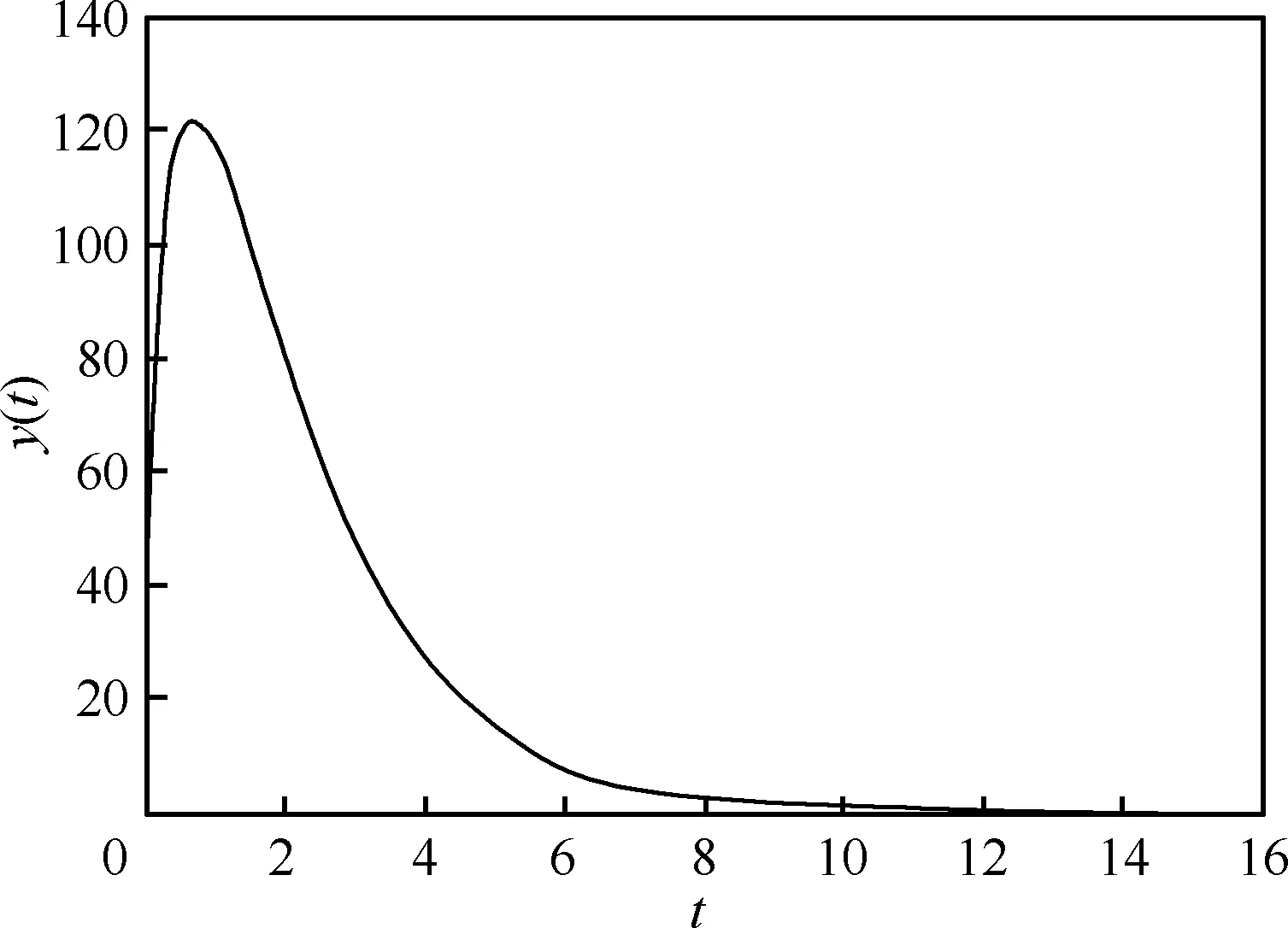
圖1 具有固定參數的Gamma函數曲線(α=240, β=1.496, θ=5.96)Fig.1 A Gamma curve with fixed parameters (α=240, β=1.496, θ=5.96)

將式(8)代入式(3)可得

(9)

在邊界條件mf(0)=0下求解微分方程式(9) 可得

(10)

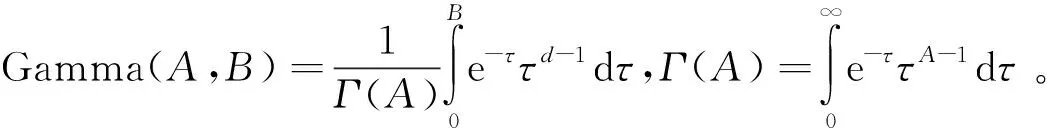
將式(10)代入式(7)，可得基于Gamma修正延時曲線的FDR增長參數化學習曲線時間函數模型為

(11)

2.2 基于Rayleigh修正延時曲線的FDR增長模型

Rayleigh曲線可以表示為[11]

(12)

由式(12)可知，Rayleigh函數是一條光滑的鈴形曲線，如圖2所示。

將式(12)代入式(3)可得

(13)

在邊界條件mf(0)=0下求解微分方程(13)可得

(14)

將式(14)代入式(6),可得基于Rayleigh修正延時曲線的FDR增長參數化學習曲線時間函數模型為

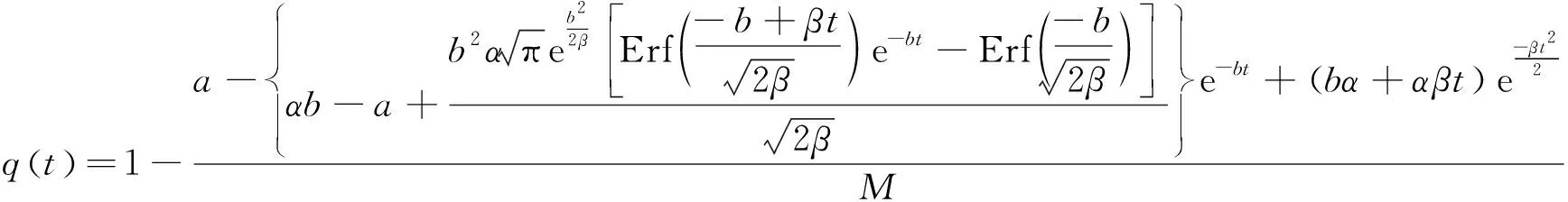
(15)

圖2 具有固定參數的Rayleigh函數曲線(α=240, β=0.111 1)Fig.2 A Rayleigh curve with fixed parameters (α=240, β=0.111 1)

2.3 基于Delay-S修正延時曲線的FDR增長模型

Delay-S曲線可以表示為[12-13]

y(t)=αβ2te-β t

(16)

由式(16)可知，Delay-S函數是一條光滑的鈴形曲線，如圖3所示。

將式(16)代入式(3)可得

(17)

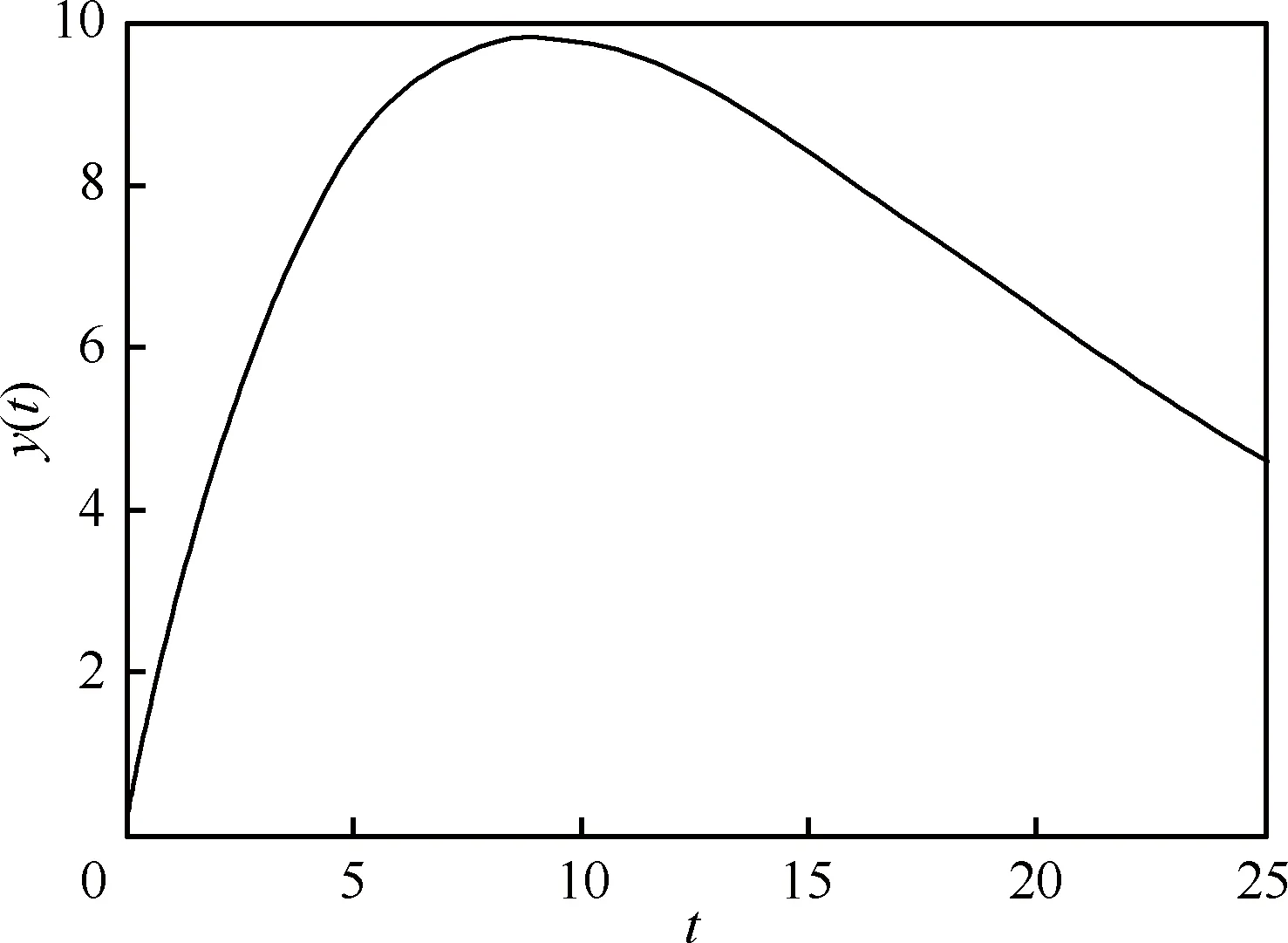
圖3 Delay-S函數曲線示意圖 (α=240, β=0.111 1)Fig.3 A Delayed-S curve with fixed parameters (α=240, β=0.111 1)

在邊界條件mf(0)=0下求解微分方程(17)可得

(18)

將式(18)代入式(6)，可得基于Delay-S修正延時曲線的FDR增長參數化學習曲線時間函數模型為

q(t)=1-

(19)

3 試驗驗證

3.1 試驗數據說明

為驗證本文所建TGM的有效性，以某型機載穩定跟蹤平臺控制系統為對象開展了測試性增長試驗，具體的試驗數據見表1。對該機載穩定跟蹤平臺開展故障模式影響及其危害性分析得到該平臺有350個功能故障。在研制階段共投入24周時間開展測試性增長試驗，在這24周時間里，通過注入313個板級功能故障，識別了86個TDL。測試性設計者分析導致TDL的根本原因并改進測試性設計，共修正了80個TDL。

基于表1所列數據，已識別TDL數量、已修正TDL數量和RTDL數量變化趨勢如圖4所示。

從圖4中可以看出已識別的TDL數量和已修正的TDL數量變化趨勢十分相似，表明兩者之間存在一定的相關性。而RTDL數量并不是常數，在測試性增長試驗的開始階段，RTDL數量不斷增長，而在增長試驗的后期，RTDL數量不斷減小，具有先增后減的鈴形變化趨勢。

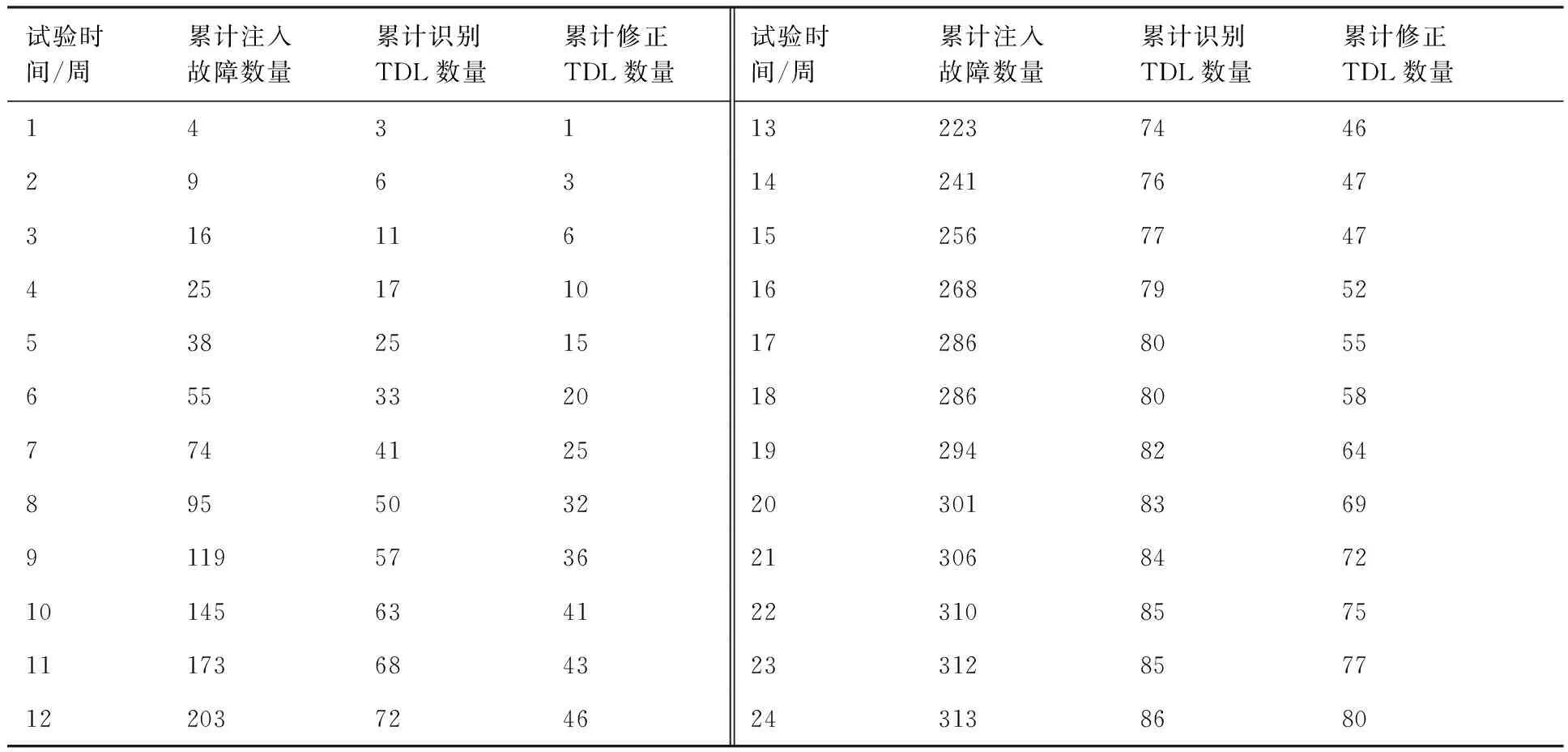
表1 某機載穩定跟蹤平臺測試性增長試驗數據Table 1 Test data of a stable tracking platform

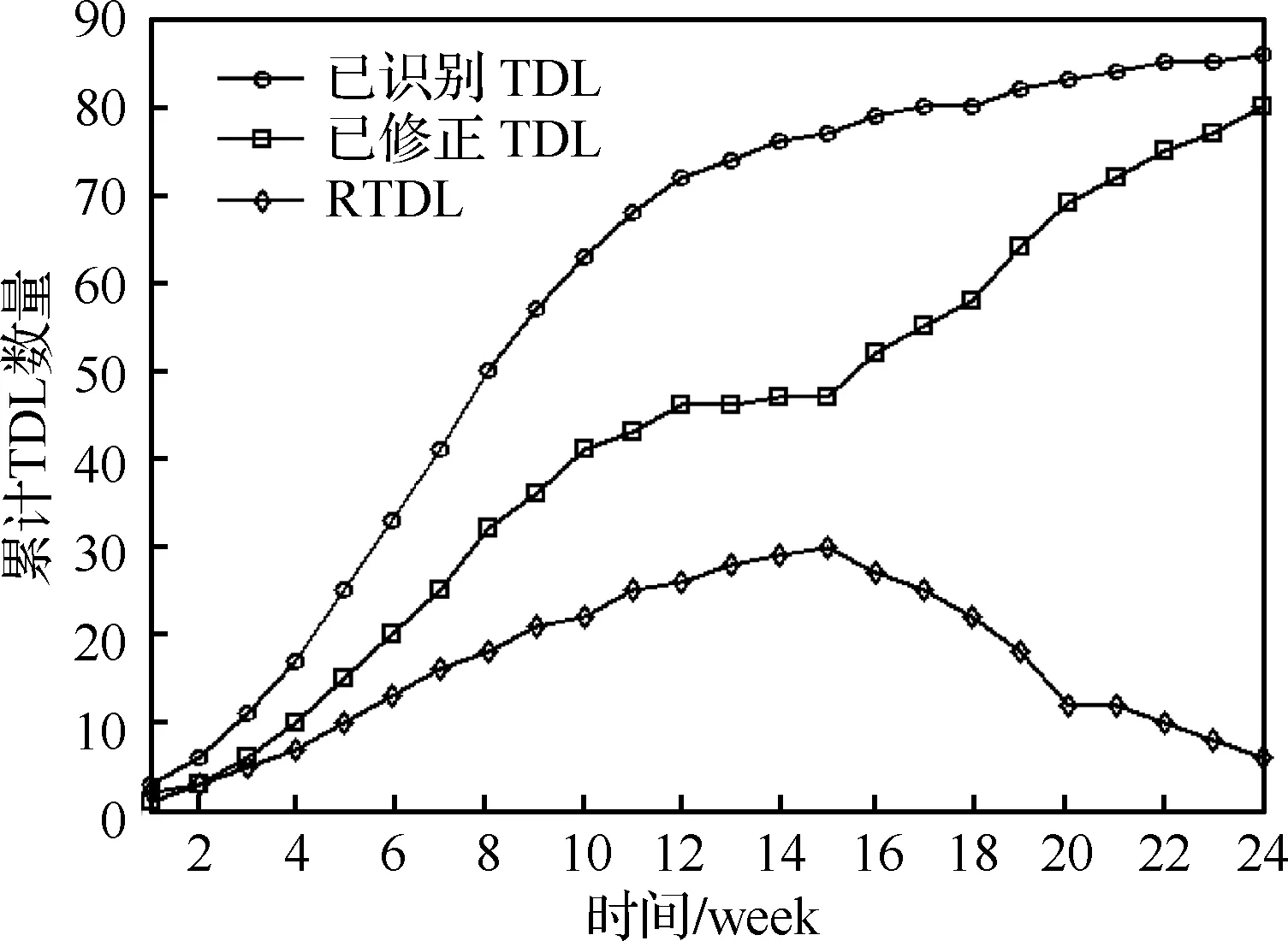
圖4 已識別TDL、已修正TDL和RTDL數量變化趨勢Fig.4 Variation tendency of identified TDL, corrected TDL and RTDL

3.2 TGM參數估計

本文采用最小二乘方法估計得到式(10)、式(14)、式(18)中的參數。

以式(18)中參數估計為例，首先計算

(20)

式(20)分別對參數集合η1={α,β}求偏導數可得

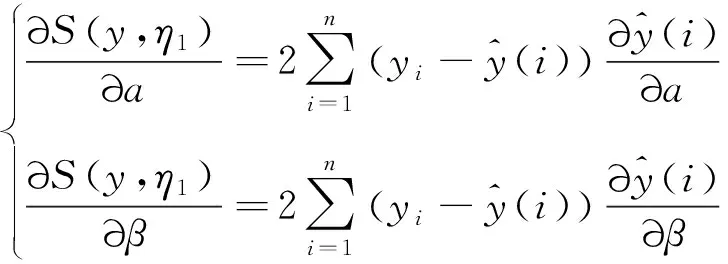
(21)

代入具體的表達式和數據，通過最小二乘求極值原理可得到參數估計結果為：α=674.46、β=0.084 8。

將求得的α=674.46、β=0.08代入式(18)后，計算可得

(22)

式(22)分別對參數集合η2={a,b}求偏導數可得

(23)

代入具體的表達式和數據，通過最小二乘求極值原理可得到參數估計結果為：a=46.03、b=0.18。

同理，可以計算得到式(10)、式(14)中具體參數估計結果，見表2。

基于表2的參數估計結果，圖5給出了實際剩余測試性設計缺陷數量變化曲線和基于Gamma、Rayleigh和Delay-S 3種鈴形曲線擬合出來的剩余測試性設計缺陷數量變化趨勢圖。

圖6給出了實際檢測到測試性設計缺陷數量變化曲線和基于式(10)、式(14)、式(18)計算得到的已檢測出測試性設計數量變化趨勢圖。

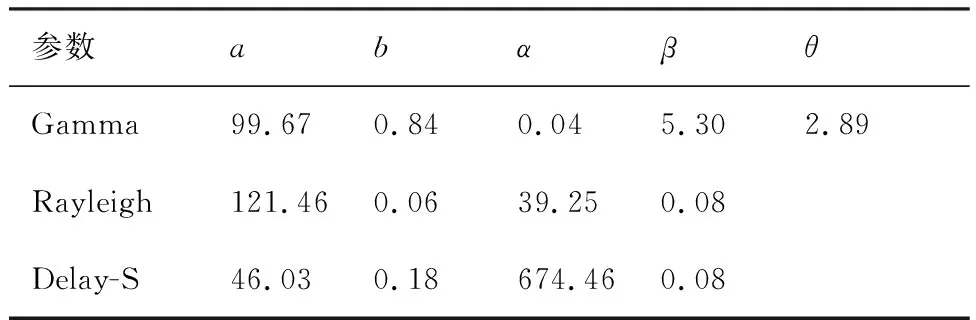
表2 最小二乘參數估計值Table 2 Estimation values based on LSE

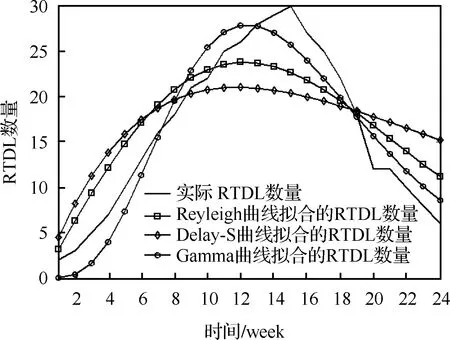
圖5 實際的和鈴形曲線擬合的RTDL數量Fig.5 Actual number of RTDL and fitting number of RTDL

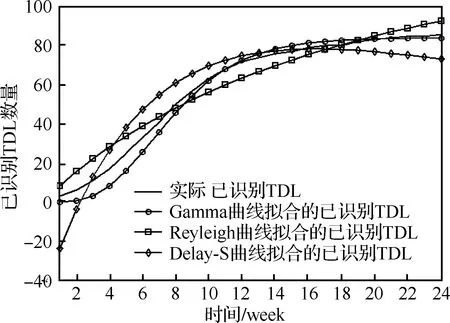
圖6 實際的和擬合的已識別測試性設計缺陷個數Fig.6 Actual number and fitting number of identified TDL

3.3 TGM評估指標

下面分別從擬合能力、估計精度和預測能力3個方面給出TGM的評價指標。

1) 誤差平方和(Sum of Square due to Error，SSE)

SSE反映了估計值和實際值之間的偏差,SSE的定義為[14-15]

(24)

式中：n為測試性增長試驗階段數；yi為經過實際測試性增長試驗后累計的RTDL數量；y(i)為測試性增長跟蹤與預計計算得到的RTDL數量。SSE越小，說明模型擬合效果越好。

2) 估計精度(Accuracy of Estimation，AE)

AE的定義為[14-15]

(25)

式中：mr為通過測試性增長試驗累計修正的TDL數量；a為估計得到的裝備系統最初包含TDL數量。AE越小，說明模型估計精度越高。

3) 相對誤差(Relative Error，RE)

RE定義為[14-15]

(26)

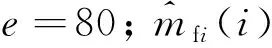
3.4 TGM效果分析

本文建立的考慮TDL修正延時的TGM，其SSE和AE計算結果見表3。

分析表3中數據可得，基于Gamma鈴形修正延時曲線建立的測試性增長模型，其SSE和AE值相對較小，表明該模型具有很好地擬合和估計能力。圖5和圖6的示意圖中也說明了這一結論。

圖7描述了基于3種鈴形修正延時曲線建立的測試性增長模型在RE這一指標的變化趨勢。由圖7可以看出，基于Gamma鈴形修正延時曲線建立的測試性增長模型計算得到的RE值相對于其他兩種模型要小，且跟蹤與預計精度能達到10-2數量級。

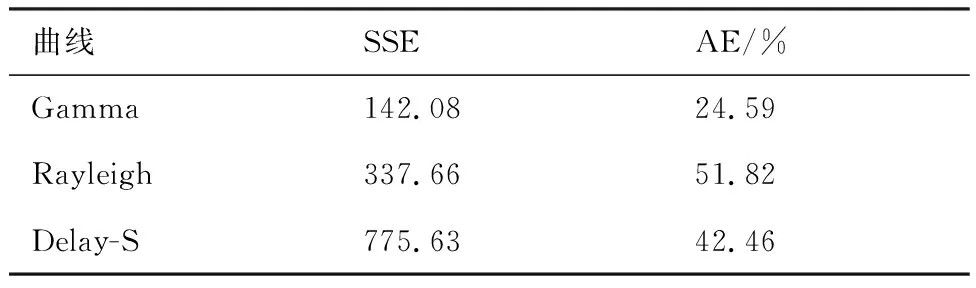
表3 3種模型指標估計值Table 3 Estimate values of SSE and AE

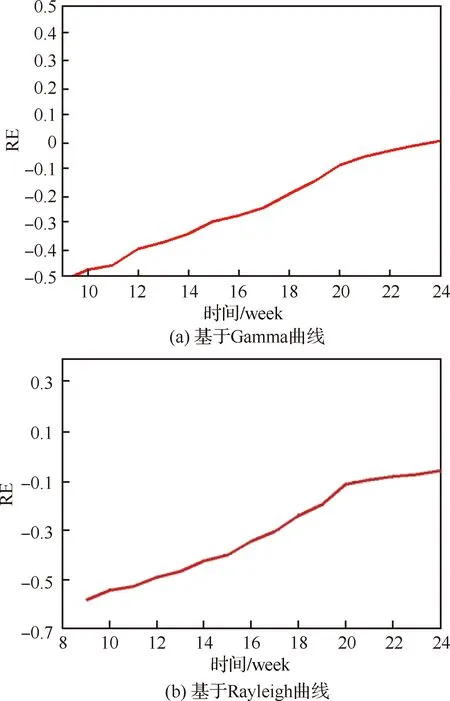
圖7 基于3種鈴形曲線的RE變化趨勢Fig.7 Variation tendency of RE based on three bell shaped curves

將表2計算得到的參數估計值代入式(11)繪制基于Gamma修正延時曲線的FDR增長試驗跟蹤與預計曲線，同時基于表1的測試性增長試驗數據繪制該機載穩定跟蹤平臺實際FDR增長曲線，如圖8所示。

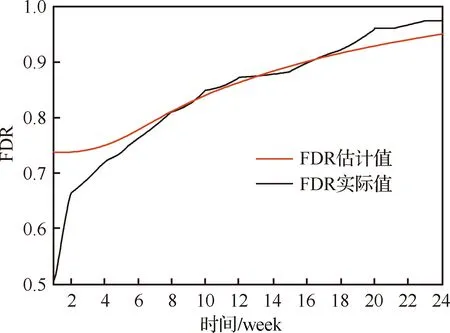
圖8 基于Gamma曲線的FDR增長曲線Fig.8 Variation tendency of FDR based on Gamma curves

4 結 論

1) 分析了剩余測試性設計缺陷具有先增后減的鈴形變化趨勢，提出基于Gamma、Rayleigh和Delay-S 3種曲線來擬合剩余測試性設計缺陷變化趨勢，數據應用表明Gamma曲線擬合精度更高。

2) 以故障檢測率為具體的增長指標，研究建立了基于3種剩余測試性設計變化趨勢曲線(Gamma, Rayleigh和Delay-S)、考慮修正延時的FDR增長模型，從擬合精度、估計精度和預測精度上給出了3個評價指標。試驗數據應用表明基于Gamma曲線考慮修正延時的測試性增長模型可以較精確地描述裝備測試性指標在測試性增長過程中的變化規律，跟蹤與預計精度能達到10-2數量級。