火炮發射藥床沖擊破碎動力學仿真研究

姜世平,黎 超

(1.江蘇大學 土木工程與力學學院,江蘇 鎮江 212013;2.南京理工大學 發射動力學研究所,江蘇 南京 210094)

火炮是一種以發射藥燃燒產生的氣體壓力拋射彈丸戰斗部的武器系統,大量裝備于各國陸、海、空各兵種。未來戰爭中,火炮武器系統的地位仍然是不可替代的:①火炮的經濟性良好,發射成本相對較低,機動性好,生存和抗干擾能力強;②在現代戰場上,火炮是近程攔截入侵導彈的有效手段之一;③火炮武器系統具有火力密集、反應迅速、可以發射智能彈藥和靈巧彈藥實施精確打擊等特點。由此可見,火炮武器系統仍然是未來各國大力發展的重要軍事裝備之一。

在武器系統的研制和使用過程中,安全性總是必須考慮的第一要素。自上世紀50年代以來,世界主要軍事強國在火炮的研制、實驗、演習和作戰過程中,都發生過膛炸事故,圖1所示為某火炮膛炸事故現場。膛炸事故會造成炮毀人亡,不但不能消滅敵人,反而使己方受到嚴重損失[1]。

圖1 火炮膛炸事故現場

國內外學者多年的研究發現,發射藥引起膛炸的主要原因是彈底藥床被點燃前受到燃氣流的沖擊作用產生了破碎[1-2]。由于火炮發射是一個極其復雜的瞬態過程,難以通過實驗途徑來獲得沖擊破碎后的發射藥床,進而分析發射裝藥引起膛炸的主要機理[1,3]。發射藥床含有成千上萬顆發射藥粒,用數值模擬方法再現彈底發射藥床沖擊破碎過程,首先遇到的問題就是如何模擬發射藥床的堆積、藥粒之間的接觸判斷、計算參數的選取,以及如何計算破碎發射藥床的表面積,這些難題至今都沒有得到有效解決[4-6]。

1 發射藥床自然堆積模擬

為了模擬發射藥床在沖擊載荷下的破碎過程,必須先獲得發射藥床的密實堆積模型。可以通過構建幾何的方法獲得發射藥床的初始堆積模型[6-7]。由于該方法主要基于藥粒在空間的幾何位置關系,而沒有考慮力學機理下平衡狀態,所以其整體結構比較松散。本文通過三維散體系統動力學方法獲得了發射藥床的密實堆積構型[1],如圖2所示。

圖2 火炮發射藥床的密實堆積模型

2 發射藥粒離散模型及運動方程

2.1 離散模型

離散單元法的基本思想是將連續體離散成剛性球單元的集合,任意2個球單元之間用一個彈簧組連接,介質的損傷、破壞是通過彈簧的變形、斷裂來體現的,且小球單元是其發生破壞時的最小單位[1,8-9]。按照上述方法,將發射藥床中藥粒離散成大小相同的剛性球體單元系統,如圖3所示,在沖擊載荷的作用下,球體之間必然會經歷接觸、擠壓、破碎這一過程。

圖3 火炮發射藥床的離散模型

2.2 離散單元的接觸判斷

在圖3中,被離散后的發射藥床是由大量球體單元組成的系統,在數值計算過程中,每一時間步長內,都需要對所有單元進行接觸與否的判斷[1],若2個單元之間存在接觸,則需要計算二者之間的接觸力。建立笛卡爾坐標系OXYZ,如圖4所示。系統中任意散體單元i的質心在坐標系中的坐標為(xi(t),yi(t),zi(t)),散體i所占據的空間為閉集Ωi;任意散體單元j的質心在坐標系中的坐標為(xj(t),yj(t),zj(t)),所占據的空間為閉集Ωj;當Ωi∩Ωj=?時,散體i和散體j沒有接觸,這時2個散體之間不會產生相互作用的接觸力;當Ωi∩Ωj≠?時,散體i和散體j之間發生接觸。

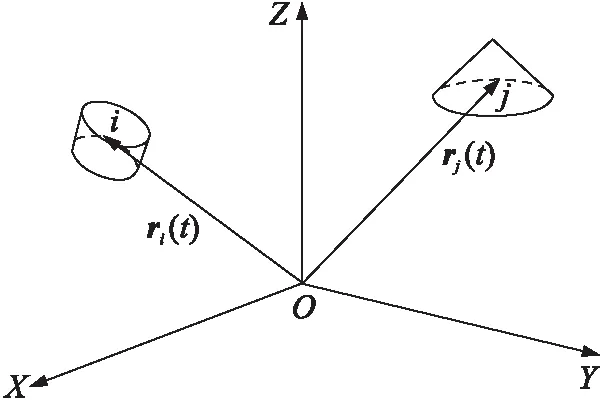
圖4 散體單元在空間的位置

對于球狀的散體單元系統,任意2個球體之間接觸的判據為:球心之間的距離dij小于或等于兩者半徑之和,即

(1)

式中:ri,rj分別為球體單元i和j的半徑。當2個球體之間相互接觸時,二者之間的作用力不再為0,接觸力的具體計算方法見文獻[10]。

2.3 離散單元的運動方程

在圖3中,被離散后的發射藥床是由大量球體單元組成的散體系統,以任意離散單元i為分析對象,在每個時間步長內散體單元i可能同時與多個離散單元接觸,隨機選取接觸單元j。在空間中,建立如圖5所示的靜參考系OXYZ,動系的原點選在離散單元i的球心o,以離散單元i的球心指向單元j的球心為動參考系的x軸,過o點取一垂直于x軸且與X-Y平面平行的直線為動參考系的y軸,根據右手螺旋法則,動參考系的z軸如圖5所示。

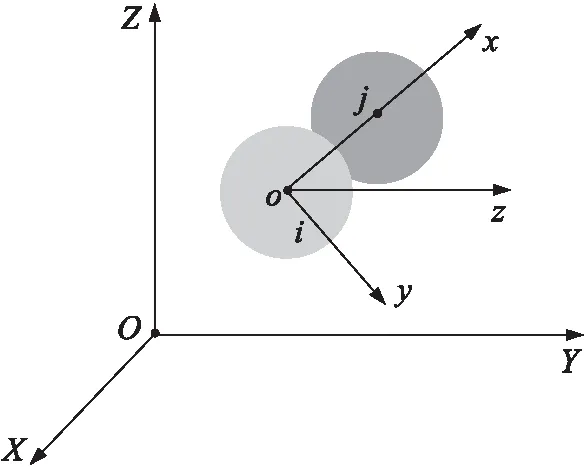
圖5 坐標系

離散單元i在靜參考系OXYZ中的平動方程為

(2)

單元i在動參考系oxyz中的轉動方程為

(3)

3 離散單元法計算可靠性的驗證

為了驗證上述模型的計算可靠性,在相同的計算參數條件下,分別應用離散單元法和有限元計算軟件LS-DYNA,對單顆發射藥粒以30 m/s的速度垂直沖擊剛性邊界的過程進行了數值模擬(離散單元法的算例取自文獻[1,9]),計算結果如圖6和圖7所示。從圖6和圖7的對比中可以發現,由于是垂直撞擊,發射藥粒的底面承受著面分布載荷,在初始沖擊速度比較小的情況下,發射藥粒發生了塑性變形,而沒有發生明顯的破碎分離。同時,從圖6和圖7中還可以發現,離散單元法和有限元法的計算結果幾乎是一致的。

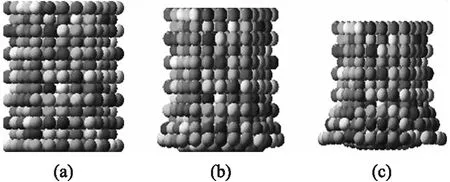
圖6 離散單元法計算的發射藥粒沖擊過程

圖7 有限元法計算的發射藥粒沖擊過程

4 離散單元法沖擊破碎仿真計算

以某型號穿甲彈為研究對象,如圖8所示,整個發射藥床含有2 854顆發射藥粒,應用離散單元法,將每顆發射藥粒離散成57個球體單元,任意時刻每個離散單元的運動由式(1)、式(2)描述;彈簧彈性力的計算參考文獻[11],彈簧的破壞參照Mohr-Coulomb準則[12],當彈簧受到的外力超過其最大承載極限時彈簧斷裂[1,8]。

圖8 某穿甲彈及其發射裝藥

為了保持仿真與試驗條件的一致性,將試驗過程中測得的彈底總壓p作為沖擊載荷,如圖9所示,相關仿真參數見文獻[9]。應用上述方法,獲得的計算結果如圖10所示,從圖中可以發現,隨著彈底總壓的逐步增加,發射藥床的破碎隨之增大,而且越靠近彈底的位置,藥床破碎得越嚴重。

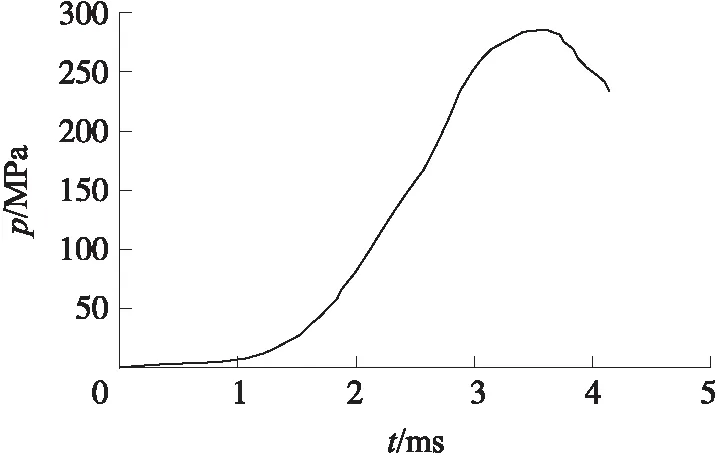
圖9 膛內沖擊載荷

圖10 膛內發射藥床在不同時刻的破碎狀況

火炮膛內的發射藥粒床破碎后,其表面積顯著增加,這是發射安全性最為關注的核心問題。但是,由于破碎后的發射藥粒形狀非常復雜,難以通過數學方法精確計算藥床的表面積變化量,只能結合某些具體的假設條件來計算每個單元的表面積(包括從藥粒中分離出來的碎塊),然后代數求和,實時計算出發射藥床在不同時間段內的表面積[1]。

根據以上原則,對不同時刻發射藥粒破碎情況進行統計,表1為統計結果,表中,t為時間,S為藥床的表面積。在初始時刻,發射藥床的表面積為8 958.97 cm2;在最終時刻,破碎發射藥床的表面積為22 615.27 cm2,與初始階段相比增加了1.5倍,說明發射藥床已經破碎得非常嚴重,在現實中極有可能導致膛炸事故的發生。

表1 發射藥床在不同時刻的表面積

5 結論

發射裝藥的破碎是導致膛炸的根本因素,由于火炮射擊過程的復雜性,難以通過實驗手段精確分析發射裝藥引起膛炸的機理。本文從理論計算的角度出發,建立了火炮發射裝藥沖擊破碎動力學仿真系統,模擬了大口徑火炮發射裝藥在膛內燃氣流沖擊作用下的破碎過程,與有限元計算軟件LS-DYNA的計算結果進行對比,驗證了該計算模型的可靠性。