炸藥底隙對炸藥裝藥發射安全性的影響

嚴 涵,于艷春,芮筱亭,陳衛東

(1.哈爾濱工程大學 航天與建筑工程系,黑龍江 哈爾濱 150001;2.東北農業大學 水利與土木工程學院,黑龍江 哈爾濱 150030;3.南京理工大學 發射動力研究所,江蘇 南京 210094)

隨著高膛壓火炮的發展,炸藥裝藥在發射過程中的沖擊過載增大,容易使炸藥在發射狀態下發生膛炸。因此,炸藥的發射安全性問題具有重要的研究價值[1-4]。國內外大量的實驗結果和理論研究成果得出較為一致的結論,即底隙是導致炸藥裝藥發生膛炸的主要因素。底隙中的殘留空氣受到膛內高壓載荷的作用,使空氣被壓縮,炸藥底部形成高溫熱點,同時會加熱相鄰的炸藥層。底隙中殘留空氣受壓縮程度越大,炸藥底部的熱點溫度越高,引起炸藥早炸和膛炸的幾率越高。

美陸軍彈道研究所采用BRL激勵器實驗研究裝置,進行了多年的模擬實驗研究,發現底隙是引起炸藥裝藥在發射環境下膛炸的主要因素[5]。在國內,很多學者開展了底隙對發射安全性影響的研究工作。肖作智等[6]進行了B炸藥試樣的水試驗,試驗結果表明,底隙能夠引起炸藥膛炸。李文彬等[7]采用有限元的方法模擬了當底隙存在時炸藥在發射過程中的應力分布,研究了不同時刻、不同底隙厚度對炸藥應力分布的影響。張濤等[8]研究了不同裝藥工藝對炸藥安定性的影響,分析了影響炸藥安定性的原因。李瑞靜[9]研究了炸藥缺陷對炸藥性能的影響。王豪[10]對炸藥裝藥的發射安全性計算進行了研究。雖然學者們在相關領域做了大量的研究工作,但定量分析炸藥底隙對炸藥安全性影響的相關文獻相對較少。

廣義黏彈性統計裂紋本構模型描述了微裂紋的擴展機制,將裂紋體與廣義黏彈性體耦合在一起,描述炸藥的黏彈性力學性能及其損傷過程,更加真實地反映了炸藥的力學特性。有限體積法是一種被廣泛應用于計算流體力學領域的數值方法,近些年,該方法在固體力學領域也得到了較好的發展。由于有限體積法采用時域的顯式積分算法,因此特別適用于求解爆炸、沖擊等高度非線性問題。因此,本文基于廣義黏彈性統計裂紋本構模型,采用有限體積法研究了炸藥在壓力載荷的作用下,底隙對炸藥發射安全性的影響,定量地分析了底隙中殘留空氣的壓縮量對炸藥內部應力、溫度及點火情況的影響。

1 有限體積法

本文采用顯式的有限體積法開展炸藥發射安全性研究。顯式算法是基于動力學方程,無需迭代,計算速度快,所需內存少,容易收斂;數值計算過程容易實現并行計算,程序編制簡單,且具有較好的穩定性,尤其適用于求解高速動力學問題,諸如沖擊、爆炸和碰撞等高度非線性問題。

與有限元法類似,首先需要對求解域進行離散,形成有限體積法的控制體積。由于顯式積分算法基于動力學方程,所以有限體積法的離散過程是將動力學方程在控制體積內積分,最終建立離散方程。

如圖1所示的控制體積V,由3-4-5-6-7-8-9-10-11-12共同圍成,D為該控制體積的中心。

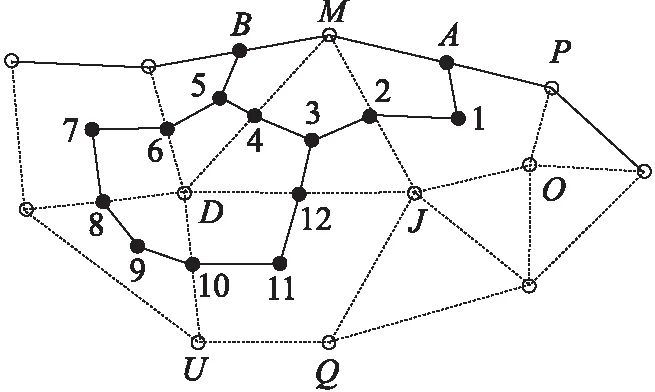
圖1 控制體積的示意圖

將動力學方程在控制體積內積分,得:

(1)

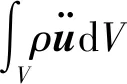
(2)

式中:Fi為力Fs在3個軸的分量;σil為應力張量;nl(l=1,2,3)為單元表面S的外法線向量n的分量,對于平面問題,方程(1)可簡寫為

(3)

式中:nj(j=1,2)為曲線的外法線向量的分量。二維平面問題的平衡方程在控制體積內的積分為

(4)

(5)

由于σxx,σyy和σxy在線性插值三角形單元里是常數。假設應變在劃分的網格單元內是常數,且其值設置在單元的中心點。通過以上的假設,如圖1所示,由M-1-2-3-4-5-B所圍成的控制體積,控制體積的中心為M,通過集中質量法進行離散化[11],詳細推導過程參見文獻[11],最終的離散方程可以寫為

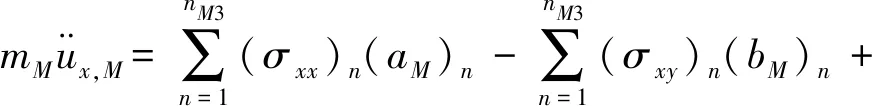
(6)

(7)

2 廣義黏彈性統計裂紋模型

本文中炸藥的本構模型采用的是廣義黏彈性統計裂紋本構模型。廣義黏彈性統計裂紋本構模型適用于碰撞、爆炸和沖擊等問題的研究。炸藥本構模型的具體推導過程見文獻[12-14],這里只給出簡要的計算公式。

(8)

(9)

式中:G(q)為第q個彈性元的剪切模量。

Dienes等[14]在研究工作中描述了裂紋的增長速率,假設裂紋的增長速率與應力強度有關,即

(10)

式中:

(11)

3 宏觀體積加熱模型

本文采用宏觀體積加熱模型描述炸藥溫度變化的模型。在計算時,對于整體的熱量變化,可以忽略宏觀體積加熱模型的熱傳導項,該模型的具體表達式為

(12)

式(12)右邊第一項為絕熱壓縮項,其中,T代表溫度,γ為Gruneisen系數,εii為應變率;第二項為由黏性效應和裂紋損傷引起的非彈性功率;其中,Pve為黏性功率,Pcr為裂紋損傷功率:

(13)

(14)

式(12)右邊第三項代表整體化學熱,其中,cV為比定容熱容,取值為1 200 J·kg-1·K-1,ΔQ為炸藥熱分解反應單位質量的分解熱,取值為5.5×106J/kg,EA為炸藥熱分解反應單位質量的活化能,EA/R取值為2.652×104K,Z為炸藥熱分解反應單位質量的指前因子,取值為5×1019s-1,ρ為密度,取值為1 810 kg/m3。

式(12)除了溫度以外的所有變量都可以通過黏彈性統計裂紋模型求出,因此,該式可以看成是關于溫度T的常微分方程,對時間進行積分即可得到一個單元的溫度狀態。

4 狀態方程

一般來說,狀態方程是用來描述材料的壓力、體積與溫度之間的關系。炸藥在外界刺激下的壓力采用狀態方程進行更新。研究不同的材料一般采用不同的狀態方程。本文計算采用固態JWL狀態方程描述炸藥壓力的更新狀態,其表達式如下:

(15)

式中:p為壓力;E為單位初始體積內能;V*為相對體積;A1,B1,R1,R2,w代表材料參數[15],取A1=77.81 kPa,B1=-5.031 Pa,R1=11.3,R2=1.13,w=0.893 8。

5 數值計算

采用有限體積法,利用黏彈性統計裂紋本構模型并結合JWL狀態方程自編程序計算了炸藥底隙在壓力作用下,炸藥內部的應力及溫度的變化,分析了底隙中殘留空氣壓縮量與炸藥底部溫升的關系,討論了底隙中殘留空氣壓縮量對炸藥點火狀態的影響。炸藥的計算模型如圖2所示。

圖2 計算模型

炸藥模型尺寸總長556 mm,最大半徑62 mm。數值模擬的材料采用PBX9501炸藥。由于廣義黏彈性統計裂紋模型中的參數很多,但目前的研究論文中僅給出了PBX9501炸藥的相關參數。下面分別給出了PBX9501炸藥的統計裂紋參數、松弛參數、黏彈性體的參數[12-13]。

統計裂紋參數:r0為裂紋初始半徑,取r0=0.03 mm,m=10,vmax=300 m/s,a=0.001 m,K0=5 kPa·m1/2。

松弛參數:1/τ(1)=0,1/τ(2)=7.32×103,1/τ(3)=7.32×104,1/τ(4)=7.32×105,1/τ(5)=2.00×106。

黏彈性體參數:G(1)=944.0 MPa,G(2)=173.8 MPa,G(3)=521.2 MPa,G(4)=908.5 MPa,G(5)=687.5 MPa。

在模擬炸藥應力及溫度變化的過程中,在炸藥底部施加壓力載荷,其壓力曲線如圖3所示。

圖3 壓力載荷曲線

采用有限體積法計算了在壓力作用下,考慮炸藥底隙時炸藥內部溫度和應力的變化規律。計算時,首先,討論隨著炸藥底部溫度的變化,炸藥內部的應力和溫度的變化趨勢及炸藥的點火情況;然后,分析炸藥底隙中空氣的壓縮量與炸藥底部溫升之間的關系;最后,結合以上兩方面的討論,分析炸藥底隙的厚度對炸藥內部應力和溫度的影響。

首先,討論炸藥底部不同的初始溫度對炸藥內部溫度和應力的影響。假設炸藥內部的初始溫度為300 K,當炸藥底部初始溫度分別為400 K,450 K,500 K,而炸藥內部其他部位初始溫度仍為300 K時,繪制了炸藥底部C(55.6,3.1)(cm)點位置處溫度和應力的時程分布曲線，同時給出了不同時刻炸藥內部的溫度和壓力云圖，計算結果如圖4～圖6所示。

①當炸藥底部初始溫度為400 K,其他部位初始溫度仍為300 K時，計算炸藥底部C點位置處溫度和應力的變化曲線及不同時刻炸藥內部壓力和溫度的變化云圖,如圖4所示。

②當炸藥底部初始溫度為450 K,其他部位初始溫度仍為300 K時，計算炸藥底部C點位置處溫度和應力的變化曲線及不同時刻炸藥內部壓力和溫度的變化云圖,如圖5所示。

③當炸藥底部初始溫度為500 K,其他部位初始溫度仍為300 K時，計算炸藥底部C點位置處溫度和應力的變化曲線及不同時刻炸藥內部壓力和溫度的變化云圖,如圖6所示。

圖4～圖6中,X,Y分別為炸藥模型在x方向和y方向坐標尺寸。

從以上計算結果可以看出,在壓力的作用下,炸藥底部的應力變化趨勢基本上與施加的壓力曲線趨勢是一致的,說明計算結果是正確的,本文提出的計算方法是可行的。當炸藥底部的初始溫度為400 K,其他部位溫度為300 K,加載時間為18 ms時,計算得到的炸藥底部的溫度升高為505 K;當炸藥底部的初始溫度為450 K,其他部位溫度為300 K,加載時間不變,計算得到的炸藥底部的溫度升高為570 K;當炸藥底部的初始溫度為500 K,其他部位溫度為300 K時,加載時間不變,得到的計算結果是,當計算到14.7 ms時,炸藥底部的溫度已經達到了預設的點火溫度,溫度突然急劇升高,此時炸藥發生了點火反應。以上計算結果說明,在底部壓力的作用下,炸藥底部溫度會升高,當溫度升高至500 K時,容易引發炸藥點火。

圖4 初始溫度為400 K的時程曲線和云圖

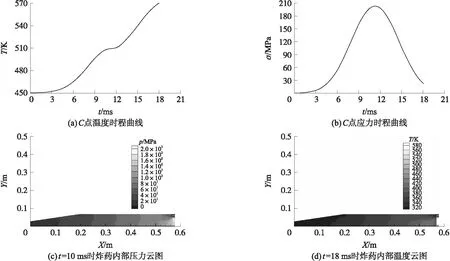
圖5 初始溫度為450 K的時程曲線和云圖

圖6 初始溫度為500 K的時程曲線和云圖

其次,研究炸藥底隙中的空氣壓縮量與炸藥底部溫升之間的關系。底隙中留存的空氣受到模擬的彈底壓力作用,迅速壓縮、加熱相鄰的炸藥層,使炸藥底部的溫度升高,從而容易引發點火。由于底隙中的空氣被很快地壓縮,假設氣體與外界來不及熱量交換,可以把這個過程近似認為是氣體絕熱壓縮過程,這樣通過計算可以得出炸藥-空氣界面間的溫度。

(16)

式中:T1,V1分別為壓縮前理想氣體的溫度和體積;T2,V2分別為壓縮后理想氣體的溫度和體積;γ為比熱比,理想氣體γ=1.4。

由式(16)可知,氣體間隙絕熱壓縮后的溫度只與氣體的壓縮比有關。如果保持壓縮后的體積不變,則初始體積越大(底隙厚度越大),壓縮比越大,壓縮后的溫度越高。本文算例考慮炸藥底隙的影響,在模擬的彈底壓力作用下,炸藥底隙中的空氣會被壓縮。設炸藥初始溫度為300 K,當底隙中的空氣被壓縮33%時,根據理想氣體絕熱壓縮狀態方程可知,炸藥底部的溫度由初始的300 K升高到354 K;當底隙中的空氣被壓縮50%時,炸藥底部的溫度升高到396 K;當底隙中的空氣被壓縮66%時,炸藥底部的溫度升高到465 K;當底隙中的空氣被壓縮75%時,炸藥底部的溫度升高到510 K。根據上面的分析可知,此時炸藥發生了點火反應,這也說明了當炸藥底隙中的空氣被壓縮超過75%時,炸藥最終會發生點火反應。底隙中空氣壓縮量η與炸藥底部溫度升高間的關系如圖7所示。這一結果與文獻[7]中得到的結論是相吻合的,從不同側面反映出底隙嚴重影響裝藥的發射安全性。

6 結論

本文采用有限體積法,利用黏彈性統計裂紋本構模型并結合JWL狀態方程,定量分析了炸藥底隙對炸藥發射安全性的影響,得到以下結論:

①炸藥在施加的壓力載荷作用下,其內部的應力變化趨勢與施加的壓力載荷曲線變化趨勢基本一致,說明本文提出的計算方法是正確的。

②定量地分析了炸藥底隙的壓縮量對炸藥底部溫升的影響。底隙中留存的空氣受到壓力作用,迅速壓縮、加熱相鄰的炸藥層,會使炸藥底部的溫度升高。依據理想氣體絕熱壓縮狀態方程,定量計算了當炸藥底隙中的空氣被壓縮超過75%時,炸藥底部的溫度能夠升高至510 K,容易使炸藥達到點火溫度。

③討論了炸藥底部不同初始溫度對炸藥內部溫升的影響。當炸藥底部(即炸藥底隙處)的初始溫度分別為400 K,450 K,500 K時,討論了炸藥在壓力作用下的點火狀態。當炸藥底部的初始溫度為500 K,其他部位溫度為300 K時,加載時間不變,得到的計算結果是,當計算時間為14.7 ms時,其溫度變化曲線突然急劇升高,溫度值無限增大,說明炸藥底部的溫度已經達到了點火溫度,發生了點火反應。