基于改進LDPC矩陣的遙感圖像重構算法研究*

許曉明

（南京理工大學 南京 210094）

1 引言

當前，在遙感數據的發現方面體現出兩個主流的趨勢：一是遙感數據發展對高數據率的需求；二是遙感探測范圍不斷擴大。而隨著當前傳感器的多樣化，以及遙感數據量的增加，要獲取更為準確的遙感圖像，必須要提高和改善遙感圖像采集系統的性能。但當前的遙感圖像采集大部分是采用Shannon-Nyquist采樣技術。這種采樣技術要求采樣的頻率需要達到信號頻譜最高頻率的兩倍以上，這樣才能保證重構信號不失真。這種采樣存在一定的缺陷，如采樣受到速率的限制，二是壓縮編碼需要舍棄大量的冗余數據，由此造成遙感圖像資源的浪費［1～5]。對此，為解決這個問題，人們提出將壓縮感知技術應用到遙感圖像的處理中，以提高圖像傳輸的速率。而研究認為，壓縮感知過程中，信號的重構是線性規劃問題。由于壓縮采樣，使得采樣數遠小于原始信號的長度，由此使得該線性規劃問題為一個方程數少于未知數，從而使其存在無數個解。為解決這個問題，人們提出采用觀測矩陣進行求解。周春佳、孫權森等研究發現，采用傳統的觀測矩陣，如高斯矩陣會增加壓縮感知的時間，同時由于觀測矩陣中的元素是浮點數，所以在存儲方面也存在一定的限制。并且由于計算量大，給硬件實現帶來極大的挑戰。另外，觀測矩陣的維數較高，實際傳輸中會有很大損耗。傳統的高斯隨機矩陣、隨機稀疏矩陣等的構造都不簡單，即在矩陣高度稀疏且元素二值化方面較為復雜。因此，結合遙感圖像采集處理的需求，本文提出一種LDPC的觀測矩陣方法。

2 LDPC觀測矩陣構造

2.1 LDPC編碼

LDPC碼為一種具有系數校驗矩陣的線性分組糾錯碼，也可用零空間的稀疏矩陣形式表示。在校驗矩陣中，通常只有少數的元素用“1”表示，其中大部分的元素是用“0”表示的一個稀疏矩陣。而LDPC碼自身的低密度，也源于校驗矩陣自身的稀疏性。在LDPC碼中，可以分為兩類［6]：一類是不規則的LDPC碼，其校驗矩陣中的各行和各列的零元素個數不同；另外的一類則是規則的LDPC碼，即在各列和各行中，零元素的個數相同。式（1）為一種規則的LDPC碼所構造的校驗矩陣（10，2，4）。

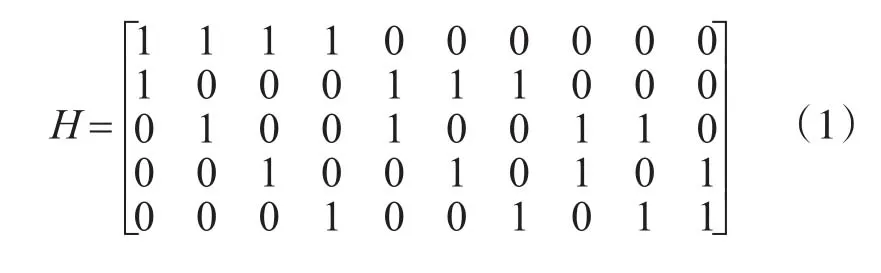
2.2 LDPC校驗矩陣構造

通過式（1）看出，通過LDPC構建的校驗矩陣是一個由“0”和“1”組成的一個稀疏二值矩陣。在該矩陣中，各列之間盡可能的線性無關，因此在壓縮感知的過程中可以作為觀測矩陣來應用。而在觀測矩陣的構造過程中，要求盡可能避免出現長度為4的短環。另外，環長度越長，構造的校驗矩陣則性能越好［7]。為構建校驗矩陣，仁恩提出了隨機構造法和結構化構造法。在本文中，則采用隨機構造法中的Mackay法對校驗矩陣進行構建［8]。以列重3，碼率為1/2為例，其具體的構造如圖1所示。

圖1 Mackay1A構造法示意圖

根據圖1的構造可以看出，采用y1A構造法后，得到的矩陣行重為6。

2.3 LDPC觀測矩陣的構造

結合上述理論的啟發，本文希望借助LDPC校驗矩陣構建一個簡單且效果優的觀測矩陣。對此，采用Mackay 1A構造法中的左半邊利用Gallager構造法，從而將兩者全部級聯在一個矩陣當中。具體構造步驟為

輸入：矩陣行數、列數、列重、行重，即M、N、γ和、ρ

1）構造子矩陣H1，設定其行數和列數分別為：M／γ、N-M；H1的第i行的“1”直接從 ( )i-1K+1開始到第iK開始排列，其中的K=r×M／N；

2）將子矩陣H1中的各列順序進行隨機置換，進而生成（γ一1）個新的子矩陣，用Hi表示，

3）將γ個子矩陣按照矩陣列的方向，合成一個新的大小的矩陣，用Φ1表示；

4）構造大小為M×M的隨機二值矩陣Φ2，使其列重大小為γ，其行重盡可能的相等；

5）將矩陣Φ1和矩陣Φ2進行級聯，繼而得到M×N的校驗矩陣Φ。

通過上述的構造，充分結合了傳統的Mackay矩陣和Gallager矩陣構造的優點，提高了重構時間。

3 LDPC觀測矩陣改進

在對上述的構建工程中，我們發現LDPC編碼構造的觀測矩陣，與傳統的隨機稀疏二值觀測矩陣相比，在計算的復雜度上都沒有明顯的優勢。因此，要減少計算的復雜度，簡化觀測矩陣的構造，嘗試結合對角塊矩陣。對角塊矩陣與其他觀測矩陣相比，存在明顯的優勢，就是只需在對角線的位置放置少量的矩陣快［9]。由此，這樣可以極大地減少圖像重構過程中的計算量，提高計算的速度。同時，為提高后期圖像采集過程中硬件的實現效果，去掉隨機置換過程。具體構造為假設傳統置亂對角塊矩陣存在L個的對角塊矩陣，用A0=diag(a1，a2， ...，ak1) ，B0=diag(b1，b2， ...，bk1) ，…由此，通過L種不同的置亂方式，可以生成觀測矩陣Φ。在該觀測矩陣中，LDPC矩陣塊為該矩陣的一個子矩陣，并且其每個對角線的位置的子矩陣都是相同的。具體如圖2所示。

由此，通過這種方式大大減低了構造的難度，也提高了計算的效率。而在圖2中也可以看出，其中的每個LDPC對角塊是相互獨立的，且LDPC塊的個數為k=N/M。

4 仿真實驗對比

4.1 圖像質量評價指標

為驗證對角塊觀測矩陣與其他觀測矩陣的優勢，本文參考相關的文獻，以PSNR和SSIM作為主要的參考指標。

4.1.1 峰值信噪比（PSNR）

PSNR為一種用于圖像質量評價的客觀測量方法，其主要是通過對原圖像和經過處理后圖像的均方差相對于（2n-1）2的對數值，以此來衡量經過處理后的圖像的質量。該值越大，說明原始圖和經處理后的圖之間越相似。

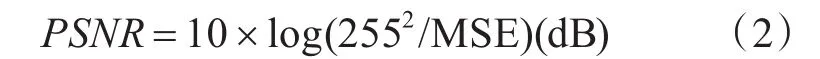
4.1.2 結構相似度（SSIM）

研究認為自然圖像本身是高度結構化的，并且其像素之間存在很強的依賴性，并且在圖像中包含了大量的視覺景象信息。因此，人們提出基于圖像結構的相似度。其具體的計算為

其中，SSIM∈（0，1），取值越大，說明相似度越高，重構效果越好。

4.2 實驗方案

為驗證上述的改進效果，采用了兩組實驗對圖像效果進行評比。

實驗1：

選擇經典灰度測試圖像Lena進行重構，圖像分辨率為512×512像素。在對圖像進行重構過程中，首先對圖像進行分塊，然后通過不同的觀測矩陣對圖像進行采樣，最后對圖像進行重構。圖像分塊采用DCT字典，圖像重構方法采用OMP算法。同時每種方法測試200次，然后比較每種方法的PSNR和SSIM值。

同時，用16×64的觀測矩陣對Lena測試圖像進行重構，從而得到如圖3的重構結果。

通過圖3看出，采用LDPC對角塊矩陣得到的圖像重構效果要明顯好于采用其他觀測矩陣得到的圖像［10]。而為了更好地更為客觀地分析重構質量，通過實驗得到PSNR和SSIM指標。具體見圖4。

圖3 不同觀測矩陣對Lena的重構結果

圖4 不同觀測矩陣重構Lena圖像的評價指標

實驗2：

對圖5的512×512的某遙感圖像進行重構，稀疏基同樣采用8×8原子大小的DCT字典，重構算法采用 OMP［11～12]，觀測矩陣采用 16×64 大小。通過重構得到圖6的遙感圖像。

圖5 山脈遙感圖像

通過重構，得到圖6的重構結果。對圖像6的重構看出，采用對角化的觀測矩陣得到的重構圖像較清晰。同樣通過多次試驗對PSNR和SSIM的統計，得到表1的結果。

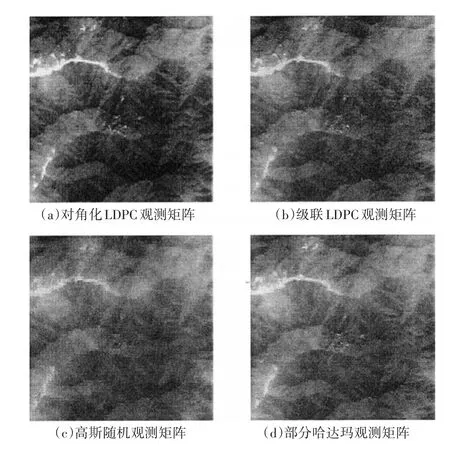
圖6 重構結果

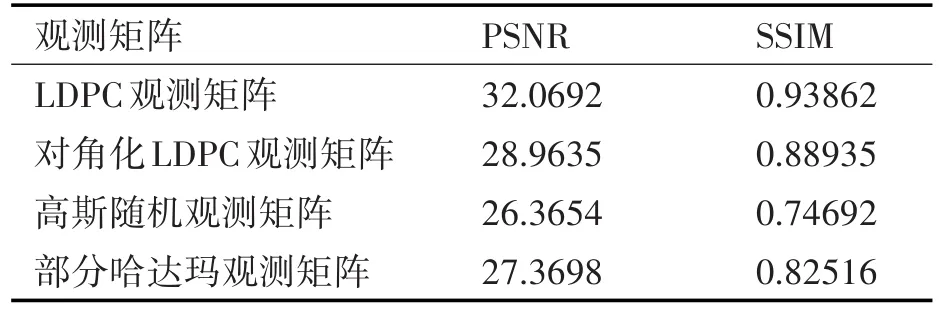
表1 四種不同觀測矩陣重構的評價結果

綜合比較，對角化LDPC觀測矩陣的重構效果優于其他同等規模的觀測矩陣重構效果。

5 結語

通過上述的研究看出，LDPC校驗碼在圖像重構方案具有較強的優勢，借助其優勢取代了傳統置亂對角塊矩陣當中的對角塊，并簡化了觀測矩陣。同時，通過仿真也驗證了采用LDPC校驗碼對對角塊矩陣的構建具有很強的優勢，在相同規模的觀測矩陣下，對角塊化后的LDPC觀測矩陣得到的重構遙感圖像更清晰。