大學英語四級成績預測建模與分析

【摘要】以本校16級學生為研究對象，在2017年12月首次參加四級考試的學生中隨機選取100名樣本，收集整理了他們大一兩次期末成績、平時成績、高考成績和CET-4考試成績，利用軟件Excel和SPSS，定量分析影響CET-4成績的諸多因素之間的關系，建立多元線性方程模型，為今后CET-4成績的預測、學校教學和學生管理提供參考。

【關鍵詞】CET-4;相關性;多元回歸方程

【作者簡介】金靈，天津體育學院運動與文化藝術學院。

一、研究背景

大學英語四級考試（College English Test Band 4， 簡稱CET-4）始于1987年，是教育部高等教育司主持的全國性的教學考試。經歷了三十多年的改革發展，四級考試已經成為反映學生英語水平和學校教學管理水平的一個重要指標，同時也是用人單位招募新人的一個重要參考，其重要性不言而喻。

眾所周知，學習的結果與學前基礎和學習過程有關。基于此，本文作者做出猜測，即大學英語四級成績可能和學生高考英語成績和大學英語課程成績相關。那么，四級成績是否與高考英語成績、大學英語課程學業成績有關？四級成績與高考英語成績、大學英語課程學業成績之間能否建立出一個多元回歸的數學模型？該模型又在多大程度上可以預測四級成績？為了回答上述問題，本文借用社會科學統計軟件包（Statistical Product and Service Solutions， 簡稱SPSS），將學生高考英語成績與四級成績、期末卷面成績與四級成績、平時成績與四級成績逐一做相關性分析，建立了四級成績與高考成績、平時成績、期末卷面成績之間的多元回歸預測模型，并對回歸模型的合理性和回歸系數進行了檢驗，以期為學校英語教學和學生管理提供參考。

二、研究方法

1.研究對象。本文以2017年12月四級考試為依托，從中隨機選取100名16級學生并對其入校前的高考英語成績、大一兩次平時成績（簡稱平時成績1、平時成績2）、大一兩次卷面成績（簡稱期末1、期末2）和大學英語四級考試成績進行收集和整理（數據來自教務處，截止到2018年12月）。利用Excel 和SPSS統計軟件，對收集到的數據進行分析、研究和建模。

2.理論基礎。多元回歸分析是一種用于評價一個因變量和多個自變量之間關系的統計技術，其數學模型如下：

y= b1x1+b2x2+···+bnxn+c

該公式表示n個自變量共同作用于因變量y，其中bn是第n個自變量xn的回歸系數，它代表的是xn 在多大程度上可以影響因變量y， c為常數項，為方程在y軸上的截距。用此方程，如果已知b1、b2···+bn，我們就可以預測y的值。

建立多元回歸方程時應注意幾點：1.線性關系。在回歸分析中，因變量與自變量的關系應為線性關系，如果不滿足這以前提的話，我們所得到的回歸分析結果可能會過低地估計了變量之間的關系。因此在分析之前通過散點圖等方式考查變量之間的關系是十分必要的。2. 多重共線性問題。多元回歸方程要求各自變量之間有一定的互斥性。如果自變量之間高度相關，在回歸過程中會彼此削弱各自對于因變量的影響，即多重共線性。多重共線性會使回歸方程中得到的回歸系數不穩定，所以需要SPSS進行多重共線性診斷。

三、研究結果

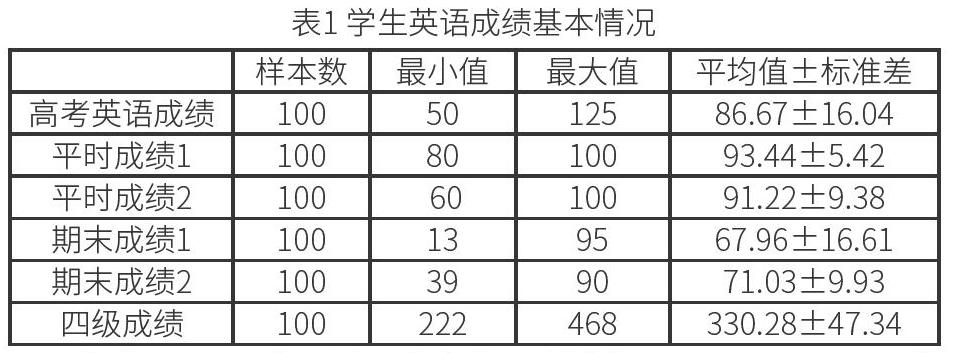
1.學生英語成績的基本情況。通過描述性分析，得到學生英語成績基本情況結果如表1所示：

由表1可以看出，樣本高考英語成績為86.67±16.04分。大一兩次平時成績分別為93.44±5.42分和91.22±9.38分，說明我校大一學生普遍出勤和課堂表現良好。大學第一次期末卷面成績為67.96±16.61分，第二次期末卷面成績為71.03±9.93分，表明我校學生在經過一年的學習后，英語水平有一定程度的上升。首次英語四級成績為330.28±47.34。

2.學生英語成績的相關性分析。在建立多元回歸模型之前，首先要對自變量（平時成績，期末卷面成績，高考成績）和因變量（四級成績）進行相關性分析，繪制散點圖。為了計算方便，本文將兩次平時成績和期末卷面成績分別取均值，再進行分析。結果如下：

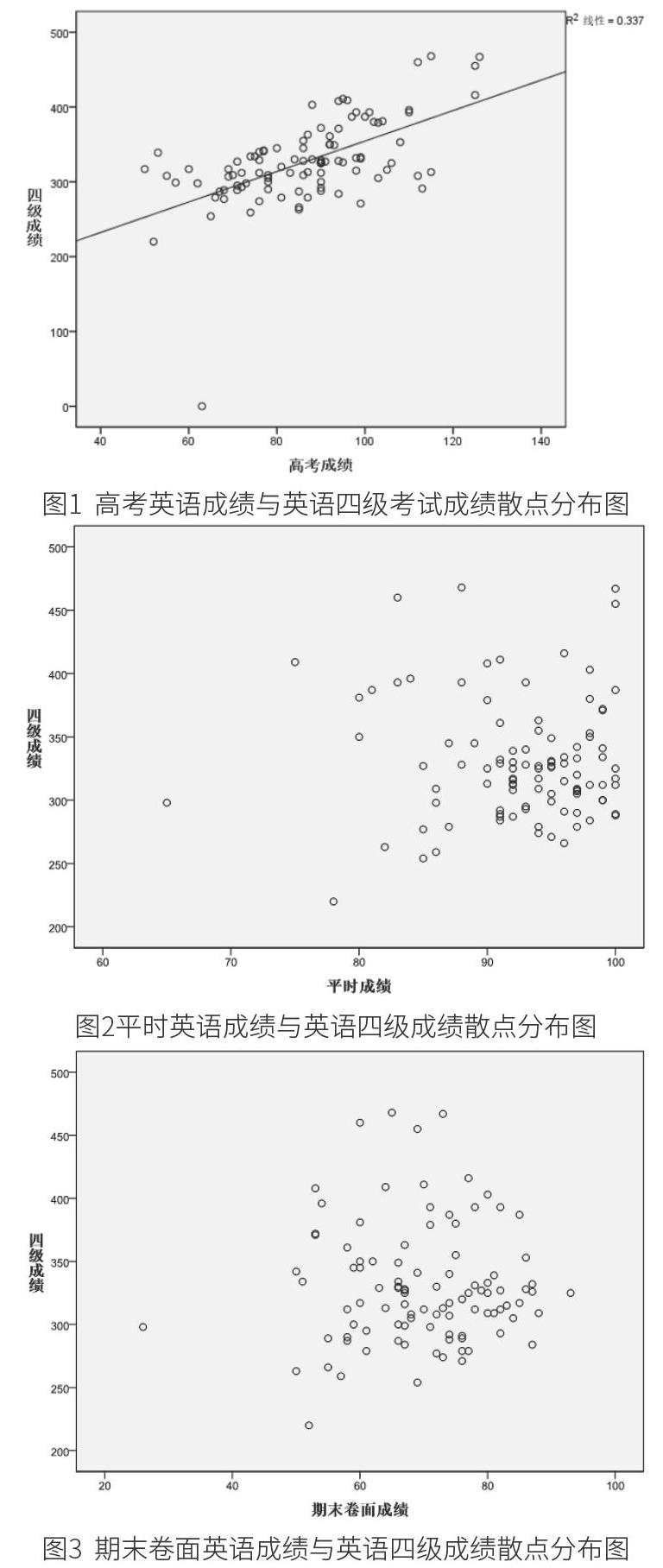
由圖1看出，高考英語成績與英語四級成績基本呈線性關系，關系點也基本分布在線性關系曲線附近，由于存在其他因素的影響，有些關系點離線性關系曲線較遠，但是基本呈線性關系，說明高考英語成績可以作為影響英語四級成績的一個因素。

由圖2看出，數據點大多集中在90～100分數段之間，大一平時成績與英語四級平時成績并不呈現出線性關系，說明平時成績對四級考試的影響并不大，可以剔除其作為因變量進入方程模型。

由圖3看出，相比平時成績，期末卷面成績的數據點分布相對規律，但也無法呈現線性關系，說明期末卷面成績和四級成績相關性很弱，可以不將其納入回歸方程。

綜上所述，只有高考英語成績和四級考試成績呈現出良好的線性關系，可以作為自變量進入方程。

3.模型建立。利用SPSS軟件對收集到的數據進行回歸分析處理，得到處理后的數據。

表2體現的是擬合優度檢驗，說明自變量和因變量形成的散點與回歸曲線的接近程度。從表中可以看出，模型擬合度為61.8%，說明回歸過程所選用的預測變量（高考英語成績）在很大程度上能夠解釋相應因變量（四級英語成績），因此可以用該模型來預測四級考試成績。

表3為單因素方差分析表，表明高考英語成績對四級英語成績有顯著的效應， F0.05（1，98）= 60.650，P<0.05。從表4系數表中我們清楚地得出高考英語成績和四級英語成績的相關系數為1.784，影響概率P值趨于0。因此，可以再次證明高考英語成績和四級英語成績的線性相關程度很高。

通過分析得出預測英語四級成績方程：