繼電保護元件重要度分析

張尚然，馮海超，劉云林，蔡青青，畢兆巖，石 果

(1.承德石油高等專科學校 電氣與電子系，河北 承德 067000；2.貴州水利水電職業技術學院 電力工程系，貴州 貴陽 551400)

在針對繼電保護系統進行可靠性評估時，往往針對整個繼保系統進行評估計算，判斷整個繼電保護系統的可靠性是否滿足要求，如果滿足要求則可行，如果不滿足要求，則需要進行改進。在可靠性評價時往往會得出，繼保系統中的某些元件對于系統可靠性的重要程度明顯比余下的元件大一些甚至大很多。也就是說，如果這些元件由于故障等原因停止工作，會給整個系統造成比較大的破壞，我們把這些元件叫做“高重要度元件”。所以，在繼電保護系統中，準確地辨別出這些高重要度元件是我們的首要任務。而元件是否可以被視為高重要度元件，主要由兩個指標所確定，他們是：1)元件本身可靠度的大小；2)元件在繼電保護系統中所在的位置是否重要[1]。明確了上述決定元件重要度的兩個條件，接下來我們引入“Birnbaum重要度”的計算方法對元件重要度進行量化計算。“Birnbaum重要度”也被稱為“伯恩鮑姆重要度”，是量化“概率重要度”的一種計算方法，通過此種計算，能夠準確地找到繼電保護系統的相對薄弱環節，從而可以為繼保可靠性的改進提供著手點[2]。

1 Birnbaum計算方法

若給定一個時間，當時刻為t時，系統的第i個元件的伯恩鮑姆重要度表達式為：

(1)

式(1)中：RS(t)是系統的可靠度，pi(t)為元件i的可靠度。

從公式(1)中可以看出，得到某個元件的概率重要度，需要將系統的可靠度函數對此元件的可靠度求取偏導數。又由于在整個系統中，每個元件是否能夠正常工作都是一個概率事件，且相互獨立，所以公式(1)也可以變換為：

RS(t)=pi·h[1i,RS(t)]+[1-pi(t)]·h[0i,RS(t)]=
pi·{h[1i,RS(t)]-h[0i,RS(t)]}-h[0i,RS(t)]

(2)

所以，伯恩鮑姆重要度表達式也能表示為：

(3)

h[1i,Rs(t)]代表如果元件i沒失效，整個系統能夠不失效的概率，h[0i,Rs(t)]代表如果元件i失效，整個系統依舊能夠運行的概率[3]。

2 算例分析

下面給出一個已知每個元件可靠性參數的繼保系統，以此作為算例進行分析。

2.1 參數和組網方案

各個元件的可靠性參數表如表1。

表1 保護元件可靠性參數

圖1是本算例的可靠性框圖。

因為元件的重要度不僅僅取決于元件本身可靠度的大小，也會因為元件在繼電保護系統中所在的位置改變而改變，為了區分此種情況，本文將不同位置的元件分別編入不同序號中，用X1～X12表示，形成了圖2中的網絡結構圖。

2.2 運算結果與分析

在給重要度定量計算時，因為網絡介質EM的結構相對簡單，其可靠性明顯高于其他元件，所以不對網絡介質進行排名。

下面將圖1可靠性框圖與圖2網絡結構圖進行對比分析，可以看出，在X1和X2位置上的合并單元MU1～MU4，其位置重要度相同，我們將之統稱為MU；同理在X3～X6位置上的交換機SW1～SW4，記作SWa；在X9和X10位置上的交換機SW5和SW6，記作SWb；在X7和X8上的PR1和PR2，記作PR；最后是位于X11和X12位置的智能終端IT1～IT6，記作IT。

合并單元 MU1=MU2=MU3=MU4 記作MU

交換機 SW1=SW2=SW3=SW4 記作SWa

交換機 SW5=SW6 記作SWb

繼保裝置 PR1=PR2 記作PR

智能終端 IT1=IT2=IT3=IT4=IT5=IT6 記作IT

因此，此番合并評估，可以將需要對比的元件分為五類即可，下面我們將橫軸時間取70 a，將公式(3)寫入MATLAB中進行計算，可得到關系圖3～圖7。

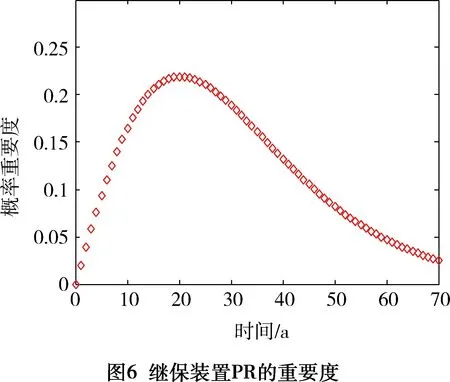
經過圖3到圖7的羅列，我們總結了一個對比結果即圖8，可以得出結論，在未來70年內的絕大多數時間范圍里，元件的重要程度可以按如下排列：

SWb>MU>PR>IT>SWa

從重要度排名可以得出，圖2的網絡結構圖里，X9位置的交換機SWb在整個繼電保護系統中重要度最高，代表了其能否正常工作對系統的可靠性影響最大，那么對此類元件可靠度進行改進提升最具性價比。

3 結論

從對上述算例分析可以得出，在繼電保護系統中，元件重要度的分析可以對可靠性的評估與改進起到促進的作用。在提高整個繼電保護系統可靠性的過程中，可以根據元件重要度分析的結果，找到改進的關鍵環節，從而提高改進效率、降低改造成本。