結合神經網絡和Q(λ)-learning 的路徑規劃方法
王 健,張平陸,趙忠英,程曉鵬
(1.沈陽新松機器人自動化股份有限公司 特種機器人BG,沈陽110169;2.沈陽科技學院 機械與交通工程系,沈陽110167)
路徑規劃是移動機器人的一項重要功能,用于引導移動機器人在地圖中自主運動。 路徑規劃的優劣直接影響移動機器人的運動效率、機器損耗和工作效率。 與其它機器學習方法不同,增強學習方法無需監督信號,而是通過智能體與環境之間的信息交互進行“試錯”,以極大化評價反饋信號為目標,通過學習得到最優或次優的搜索策略。 總體來說,增強學習的主要目標就是將狀態映射到動作的同時,最大化期望回報。
隨著增強學習理論和算法的不斷發展與成熟,應用增強學習方法解決移動機器人路徑規劃問題正成為路徑規劃的研究熱點[1]。 文獻[2]提出了改進的Q-learning 方法用于解決單個機器人的路徑規劃問題, 通過引入標志位減少了學習過程的收斂時間,提高了算法的效率;文獻[3]提出用神經網絡模型來解決最短路徑規劃問題;文獻[4]提出基于分層強化學習的路徑規劃方法;文獻[5]對基于神經網絡和POS 的機器人路徑規劃方法做了較為深入的研究。 強化學習是目前機器學習中富有挑戰性和廣泛應用前景的研究領域之一[6]。
目前,傳統的強化學習方法在移動機器人路徑規劃應用中,由于其學習初始階段對環境沒有先驗知識,往往存在收斂速度慢、學習時間長等問題。 故在此通過引入神經網絡方法, 對傳統Q-learning 算法進行改進,優化設計獎勵函數,提出了基于神經網絡的改進Q-learning 學習算法。
1 Q(λ)-learning 算法
Q-learning 是一種與模型無關的強化學習方法,在環境未知條件下,通過不斷試錯和探索,對所有可能的狀態和動作進行多次嘗試,采用數值迭代方法逼近最優解。
它以狀態-動作對應的Q(s,a)為估計函數,逐漸減小相鄰狀態間Q 值估計的差異達到收斂條件,即
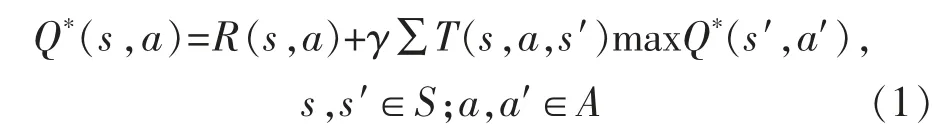
式中:S 為狀態集;A 為動作集;T(s,a,a′)為狀態s下執行動作a 后轉換到狀態s′的概率;R(s,a)為狀態s 下執行動作a 的獎勵;γ 為折扣因子。 尋找最優Q 值Q*(s,a)的搜索策略為
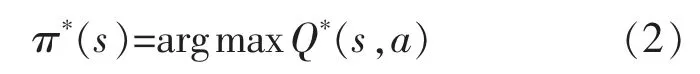
更新公式為
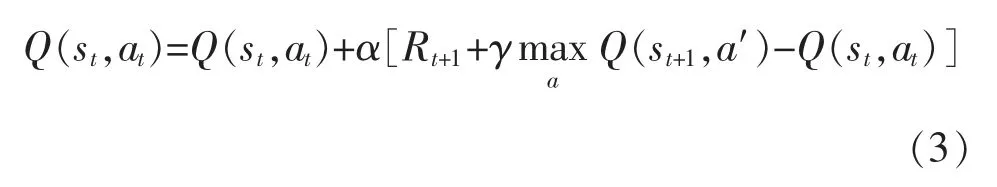
在Q-learning 算法中引入跡的思想, 能夠記錄狀態被訪問的次數,在更新前一時刻的狀態值函數時, 也能對之前的狀態值函數進行更新, 即Q(λ)-learning 算法。 其更新公式為
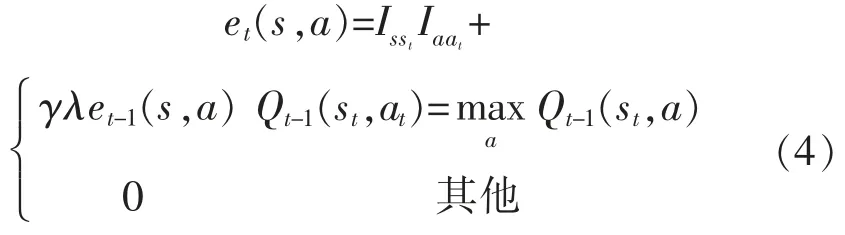
式中:Isst和Iaat為指數函數,如果s=st則值為1,反之為0。 誤差項為
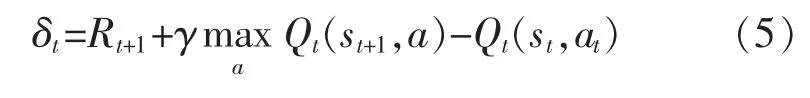
更新動作公式為
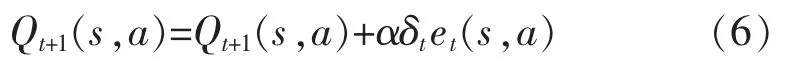
搜索函數為
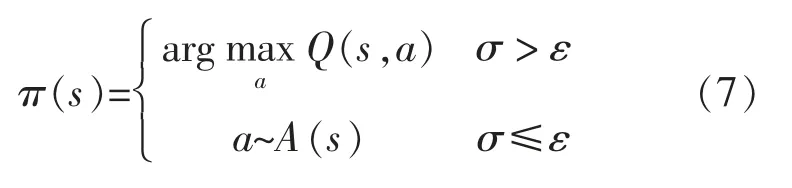
式中:σ 為0~1 之間的隨機數;ε 為探索因子,為0~1 之間的數。
2 受生物啟發的神經網絡方法
受生物神經系統中Hodgkin 和Huxley 細胞膜模型[7]與Grossberg 分流細胞模型[8]的啟發,文獻[9]提出了受生物啟發的神經網絡方法,用于解決移動機器人路徑規劃問題。 該神經網絡方法狀態方程為
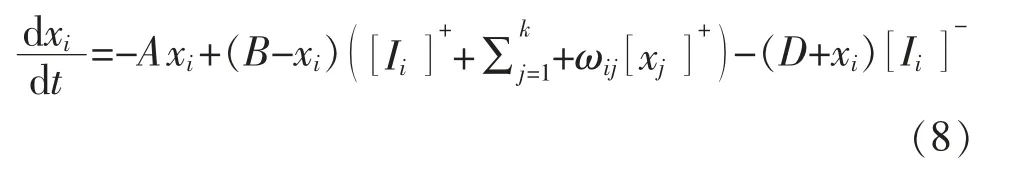
其中

式中:xi為第i 個神經元的神經活動 (神經元細胞膜的電勢);A,B,D 分別為被動衰減率、神經活動的上限和下限, 均為非負常數;和[Ii]-為第i 個神經元的刺激性、抑制性輸入;Ii為第i 個神經元內部輸入;E 為正整數,且E>>B;[]-,[]+分別為取正、取負函數。該取正、取負函數的功能為
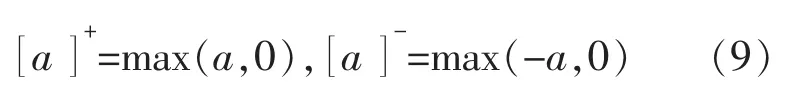
狀態方程(8)中,第i 個神經元與第j 個神經元之間的權值連接ωij為一個距離函數。 其表達式為
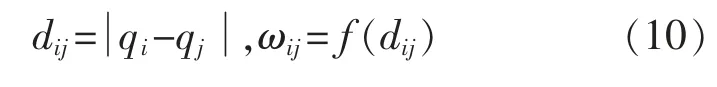
其中
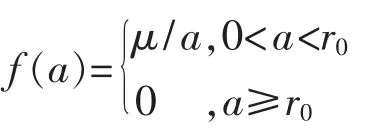
式中:dij為狀態qi和qj之間的歐氏距離;μ 和r0為正整數。
該神經網絡方法不需要學習過程,根據神經元細胞之間的信息傳遞,可以求出神經元細胞所在狀態的勢值函數。 通過實時更新勢值函數,移動機器人從初始位置沿著勢值增大的方向到達目標位置,從而得到規劃路徑。
3 結合神經網絡和Q(λ)-learning 算法
3.1 優化設計獎勵函數
在Q-learning 算法中,獎勵R(s,a)表示狀態s下執行動作a 得到的獎勵。 獎勵值的大小直接影響動作選擇的正確性和誤差傳遞的效率。 因此,獎勵函數設計的好壞,直接影響算法的收斂速度和最優解的質量。
傳統的Q-learning 算法, 一般將目標狀態的獎勵設為很大的正整數,障礙物狀態設為很小的負整數,其余狀態處的回報值均為0。這種方式的獎勵函數沒有啟發性,機器人在初期學習階段很難到達目標,導致收斂速度很慢。
在此,獎勵函數的設計采用文獻[9]所提神經網絡方法。 令狀態方程(8)中,A=10,B=D=1,E=100,μ=1,r0=2,則狀態方程轉化為
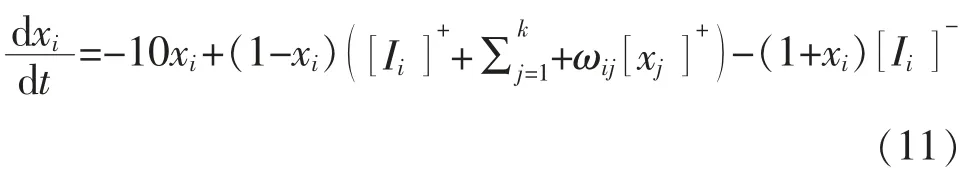
該神經網絡模型可以確保從目標狀態發出的刺激性信息,通過神經元之間的橫向連接,傳遞給該工作空間的所有狀態,而從障礙物傳出的抑制性信息只在有限的范圍內傳播。
通過狀態方程(11)可以得到每個狀態勢值,勢值矩陣為X。 將獎勵函數定義為
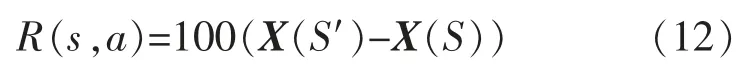
式中:X(S′)為執行下一個動作的狀態勢值;X(S)為當前狀態勢值。
3.2 算法實現流程
結合神經網絡和Q(λ)-learning 算法,具體的實現步驟如下:
步驟1利用狀態方程(11),經過k 次迭代,求出狀態勢值矩陣;
步驟2根據式(12),計算出獎勵函數R(s,a);
步驟3進行第i 次迭代計算, 最大迭代次數為n;
步驟4生成隨機數σ,執行式(7)搜索策略π(s);
步驟5執行動作a,得到獎勵R(s,a),轉移到新狀態s′;
步驟6判斷s′是否為終止狀態, 如果是則跳到步驟3 進行下一次迭代(i=i+1),不是則跳到步驟7;
步驟7根據式(5),計算誤差;
步驟8根據式(4),更新動作狀態跡,并更新其他動作狀態跡;
步驟9根據式(6),更新動作值函數;
步驟10s←s′,跳到步驟3,搜索下一個狀態。
算法完成一次訓練的流程如圖1 所示。 該算法在迭代學習之前對根據環境地圖信息進行狀態勢值計算,獲得先驗知識,以指導獎勵函數設計,從而提高算法的收斂速度和最優解的質量。
4 仿真試驗與結果分析
通過仿真試驗來驗證改進方法的有效性,試驗環境采用20×20 柵格地圖(如圖2 所示),以圖中左上角S 為移動機器人的起點, 以右下角E 為目標。圖中, 白色部分為移動機器人的自由運動區間;黑色部分為障礙物,移動機器人無法穿越該區域。
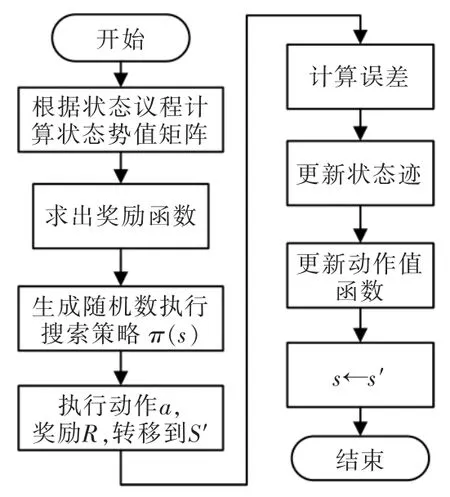
圖1 結合神經網絡和Q(λ)-learning 算法流程Fig.1 Algorithm based on neural network and Q(λ)-learning flow chart

圖2 最優策略示意圖Fig.2 Optimal strategy schematic diagram
移動機器人動作集A 包括上移、右上、右移、右下、下移、左下、左移、左上等8 個動作;狀態集包括400 個位置,障礙物和目標狀態為終止狀態。當移動機器人移動到終止狀態, 則本次訓練循環結束,重新進行下一次訓練。
采用神經網絡方法經過1000 次迭代計算得到的勢值分布如圖3 所示。 根據式(12)處理狀態勢值可以得到獎勵函數R(s,a)。
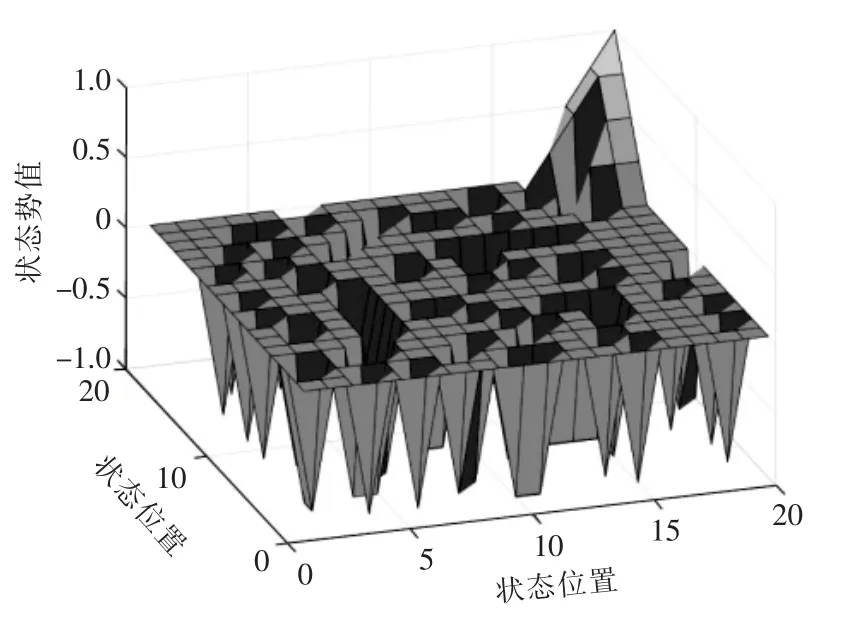
圖3 狀態勢值分布Fig.3 State potential value distribution
算法中幾個重要的參數會直接影響收斂速度。仿真試驗中,折扣因子γ 初始化為0.8,學習速率α初始化為0.05,探索因子ε 初始化為0.5,最大探索步數初始化為400。當搜索步數超過最大步數時,仍未到達終止狀態,則認為此次訓練失敗,重新進入下一次訓練。
采用經典Q-learning 方法, 在訓練32000 次時收斂, 而本文方法僅需15000 次訓練達到收斂狀態,可見收斂速度有很大的提升。 訓練完成的最優策略如圖2 所示, 從起點到終點的最優路徑如圖4所示。
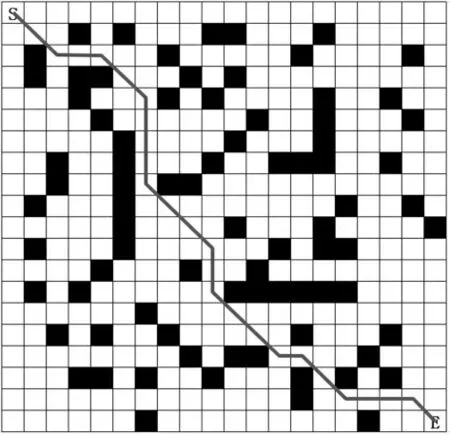
圖4 從起點到終點最優路徑Fig.4 Optimal path from start to end
采用同樣的方法,生成另外3 個障礙物分布不同的柵格地圖,使用同樣參數完成訓練。 統計移動機器人在地圖所有狀態下到達目標狀態的平均步數,見表1。
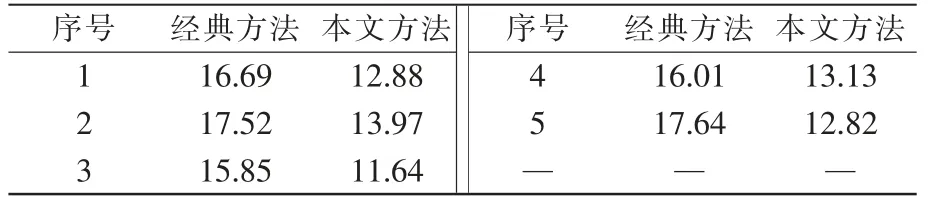
表1 兩種方法平均步數的對比Tab.1 Comparison of average steps between the two methods
移動機器人在所有狀態移動到終點的平均步數越少,說明策略越優。 由表可知,本文方法在5 次試驗中,平均次數均明顯低于經典Q-learning 方法。
5 結語
所提出的結合神經網絡和Q(λ)-learning 算法的移動機器人路徑規劃算法,通過優化設計獎勵函數,為增強學習提供了先驗知識,解決了強化學習中存在的收斂速度慢和解的局部最優問題。通過仿真試驗,本文方法與經典學習方法相比較,驗證了該方法的有效性。

