一種新型深潛器耐壓殼的非線性屈曲計算

彭 懿，韋乃琨，趙 晶，甄希金，王 浩

(1. 上海船舶工藝研究所，上海 200032；2. 上海申博信息系統工程有限公司，上海 200032)

0 引 言

深海潛水器是在各種復雜海域進行水下科學考察和開發作業的必備裝備,是人類研究開發海洋的主要技術之一。耐壓殼作為深海潛水器人員和儀器搭載平臺，其可靠性、功能性至關重要。耐壓殼的可靠性表現為抵抗海水壓力的能力，下潛越深需要抵抗海水壓力越大。功能性表現為盡可能多地搭載人員和設備，盡可能低的結構重量。李文躍等[1]對大深度載人潛水器的耐壓殼結構形式做了較深入的研究，分析了圓柱形、球形、橢球形耐壓殼的特點。隨著潛深的增加，對耐壓殼的抗壓能力要求越來越高，張呤等[2]提出了一種新型雙層耐壓殼結構，研究顯示其抗屈曲能力較單層耐壓殼有顯著提高。隨著下潛深度的增加，結構重量與自浮力之間的矛盾將變得更加突出，必須采取有效措施,嚴格控制結構重量增長幅度，以確保深潛器有效載荷不減少，保持合理的容重比以滿足功能需求。張乃樑[3]對比了圓柱、橢球、球球、球柱球3 種形式耐壓殼的容重比，得出橢球的容重比最高。圓柱形耐壓殼盡管在抗壓能力上不及球形和橢球形，但在制造工藝難度、水動力特性、成本、空間利用率等方面有明顯的優勢，因此本文選擇圓柱形耐壓殼為研究對象。

由于深潛器耐壓殼是受外部水壓力，所以屈曲是耐壓殼破壞的主要原因。受各種不同力和邊界條件約束的圓柱殼屈曲問題，國內外已有大量研究。L.H.Donnell[4]引入缺陷因子的概念討論了缺陷對軸壓薄壁圓柱殼屈曲的影響；Izhak Sheinman[5]給出了幾何缺陷縱環加筋圓柱殼在軸壓作用下的屈曲數值解；周承倜[6]和陳鐵云[7]等研究了具有初始缺陷的環肋圓柱殼在均勻靜水壓力作用下的彈塑性屈曲；Yamaki[8]系統地研究了受各種不同力和邊界條件約束的圓柱殼的彈性屈曲。為了提高抗壓能力，控制結構重量，提高容重比，本文參考了王林等[9]的研究，將圓柱形耐壓殼設計成縱環加筋圓柱形耐壓殼。耐壓殼在制造過程中外形難免有缺陷，在學術界將此種缺陷稱為初始缺陷，并用初始缺陷撓度來描述。因此問題實質上是有初始缺陷縱環加筋圓柱殼的受壓屈曲問題。彭懿[10]對具有初始缺陷的縱環加筋圓柱殼在均勻靜水壓力作用下的彈性屈曲做了較深入研究，給出了特定條件下的幾何非線性解析解。本文在上述研究的基礎上，同時考慮幾何非線性和材料非線性，用專業計算軟件對彭懿[10]的研究做了進一步探討。

1 非線性屈曲的有限元解法

由于非線性問題的復雜性，往往嚴格的數學求解是十分困難的，而有限元方法為非線性問題的數值求解提供了有效的工具。有限元方法求解非線性問題是將非線性問題轉化為一序列線性問題求解。

目前專業計算軟件對結構進行非線性屈曲計算是通過非線性靜力分析實現的。利用線性加載方法逐步施加載荷，直至結構的切向剛度矩陣變成奇異陣，可以認為結構此時屈曲，即可終止計算，并認為此時的載荷即為屈曲臨界載荷。

為了幫助理解非線性屈曲的有限元計算，下面簡單介紹基本思想[11]。

非線性計算，不能直接由線性方程組求得響應，需要將載荷分割成若干增量求解，每一增量內將非線性變量線性化，然后由線性方程組求得這一增量內的響應。但純增量法沒有考慮由線性化導致的誤差，前一增量步的誤差會累積到后一步，誤差的累積會使解明顯偏移。

與線性問題不同，無論是材料非線性還是幾何非線性，單元剛度矩陣 [ke] 與單元節點位移 g0gggggge相關。假設結構體的剛度矩陣 [Kg0gggggg] ，節點位移為 g0gggggg，外力為{R}，非線性有限元方程為：

式（1）可以寫成下面的形式：

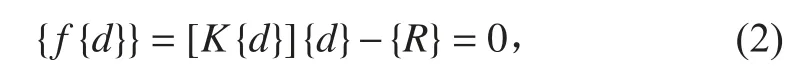
則方程 {fg0gggggg}=0的根即是式（1）的解。式（2）中[Kg0gggggg]g0gggggg 是 內 力， {R} 是 外 力， {fg0gggggg}是 內 力 與 外 力的不平衡力，只有 g0gggggg 為精確值時 {fg0gggggg}=0才成立。求解式（2）一般都采用線性化方法，把非線性問題轉化為一系列線性問題求解。即把整個載荷分為若干個子步（增量）加載，每個子步內都進行線性迭代運算。具體做法是在每個子步內用切向剛度矩陣 [KT]代替剛度矩陣 [Kg0gggggg]，這樣非線性方程式（2）就變為如下線性方程：

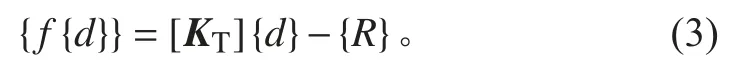
式中切向剛度矩陣 [KT]可根據應力應變曲線求得。

顯 然 將 變量 [Kg0gggggg]用 常量 [KT]代 替 會產生誤差，導致{fg0gggggg}≠0。為了消除誤差需要通過迭代運算，通常使用的迭代算法有Newton-Raphson 法和Risk 法。高良田等[12]采用Risk 法對球形耐壓殼的非線性屈曲做了計算，取得較好的結果。Risk 法被認為是目前結構非線性屈曲計算中數值計算最穩定、收斂性最好的迭代計算方法之一，本文采用Risk 法計算耐壓殼的非線性屈曲。

2 計算模型創建

2.1 物理模型簡介

物理模型數據來自于王林等所做的實驗[9]，本文只將縱筋的位置調整為內加筋，使模型的結構形式與耐壓殼的結構形式一致。模型為縱環加筋圓柱殼，模型兩端用厚鋼制法蘭密封固定。殼體半徑R=850 mm，殼體長度L=500 mm，殼體厚度t=4 mm；肋骨共有11 根，間距l =46 mm，肋骨尺寸： S1=δ ×h =6 mm×21 mm=126 mm2， δ為環筋的厚度， h為環筋的高度；縱筋位于圓柱殼內側，共24 根，沿圓周均布，間距b=222.5 mm，縱 筋 尺 寸： S2=δ ×h =4 mm ×15 mm=60 mm2， δ為縱筋的厚度， h為縱筋的高度；殼體、環筋、縱筋是同樣的材料。材料屈服極限是 σs=784 MPa，材料的彈性模量是 E =2.0 ×105MPa，材料的泊松比是 μ=0.3。

2.2 單元選取與材料模型

圓柱殼體使用殼單元，法蘭采用殼單元，縱向和橫向加強筋均采用梁單元。

由于王林等所做的實驗[9]中只給出了材料常數，沒有給出材料的應力應變曲線。在此假定材料為理想彈塑性且各向同性硬化材料，材料應力應變曲線采用雙線形。材料應力應變曲線如圖1 所示。

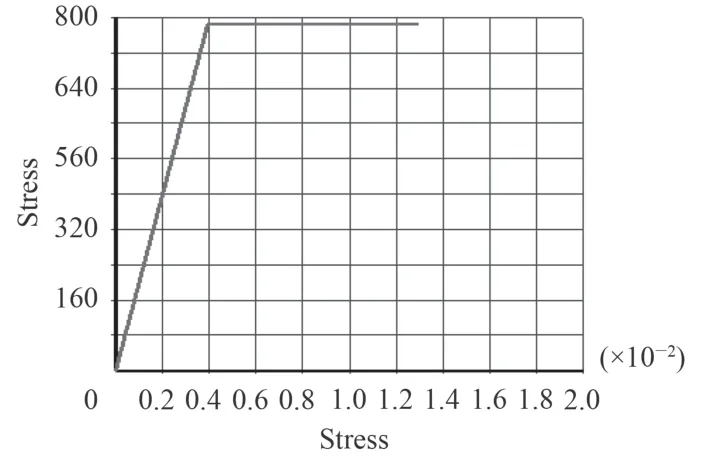
圖1 材料應力應變曲線Fig. 1 Material stress-strain curve

2.3 有限元模型

整個模型劃分為3726 個單元。法蘭用三角形網格自由劃分為678 個殼單元，圓柱面用四邊形網格劃分為1 440 個殼單元，縱向和橫向加筋共劃分為1 608 個梁單元，如圖2 所示。

圖2 非線性屈曲計算有限元模型Fig. 2 FEM for nonlinear buckling calculation

2.4 載荷和邊界條件

如圖3 所示，耐壓殼內部被剛度遠大于耐壓殼的艙壁分隔，因此可以認為耐壓殼的端面是被剛性固定的。耐壓殼外部加靜水壓力，加載方式采用分步加載，直至耐壓殼發生屈曲破環，載荷的上界取線性屈曲分析的結果6.61 MPa[10]。

2.5 初始缺陷引入

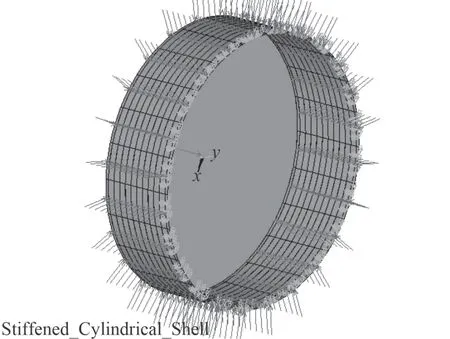
圖3 非線性屈曲計算的載荷和邊界條件Fig. 3 Load and boundary conditions for nonlinear buckling calculation

在耐壓殼或實驗模型實際的加工、裝配、焊接過程中，產生變形是不可避免的，這使結構偏離正確的形狀，產生所謂的非圓度。在學術界將這種非圓度稱為初始缺陷。無論是實際使用的深潛器還是用于實驗的模型，由于加工工藝的限制，都無法避免初始缺陷的存在。初始缺陷對屈曲的影響也發表了大量研究結果[4-7]。研究結論表明初始缺陷對耐壓殼的屈曲有明顯影響，顯著降低了耐壓殼的臨界屈曲載荷。因此，在耐壓殼的屈曲計算中必須考慮初始缺陷。張菊等[13]對耐壓殼初始缺陷的檢驗方法、檢測原理、偏差計算做了探討，但對耐壓殼的初始缺陷的精確數學描述是很困難的。為此國內外研究者[14]在研究耐壓殼的非線性屈曲時的一致做法是將1 階模態通過適當變換作為初始缺陷。本文也使用此方法。初始缺陷引入分為2 步：第1 步進行線性屈曲計算，得到1 階模態（見圖4）并將1 階模態的節點位移導出；第2 步將節點位移做適當變換引入有限元模型得到具有初始缺陷的有限元模型。至此就得到用于非線性屈曲計算的有限元模型。

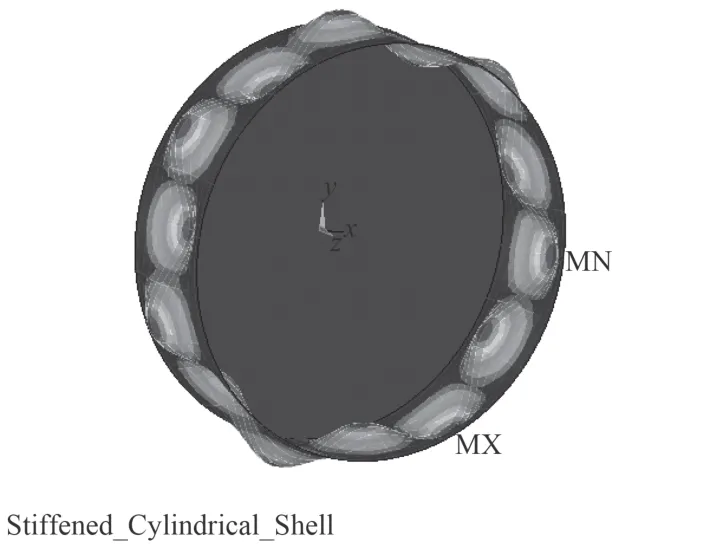
圖4 一階屈曲模態節點位移圖Fig. 4 Displacements of nodes under first order buckling mode

3 計算結果

將節點位移做適當變換引入有限元模型，分析了初撓度幅值分別為：0.8 mm，1.0 mm，1.5 mm，2.0 mm的縱橫加筋圓柱殼的非線性屈曲臨界載荷。分析結果如圖5～圖8 所示，并將各初撓度下的臨界載荷用表1列出。圖5～圖8 中的縱橫加筋圓柱殼軸向半波數為1，周向整波數為7。這與王林等所做的實驗[9]結果一致，說明邊界條件和加載方式是合理的。王林等[9]給出基于線彈性理論的完美耐壓殼臨界載荷解析解是6.56 MPa，實驗得出的臨界載荷是4.61 MPa，顯然基于線彈性理論的解析解要高于實驗值。非線性屈曲計算考慮了模型實際存在的缺陷，因此所得的結果小于解析解，而更接近實驗值。

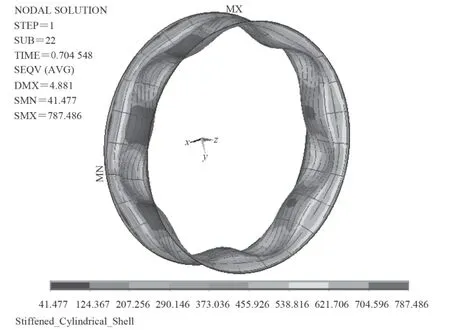
圖5 初撓度幅值為0.8 mm 的非線性計算結果Fig. 5 Nonlinear calculation results under initial imperfections amplitude 0.8 mm

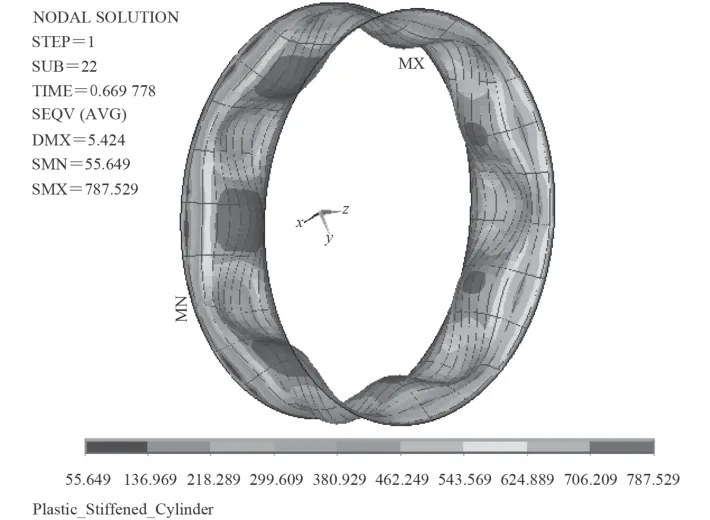
圖6 初撓度幅值為1.0 mm 的非線性計算結果Fig. 6 Nonlinear calculation results under initial imperfections amplitude 1.0 mm

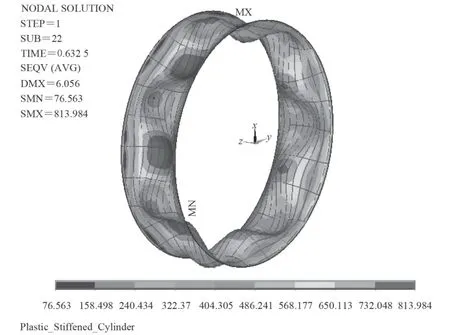
圖7 初撓度幅值為1.5 mm 的非線性計算結果Fig. 7 Nonlinear calculation results under initial imperfections amplitude 1.5 mm

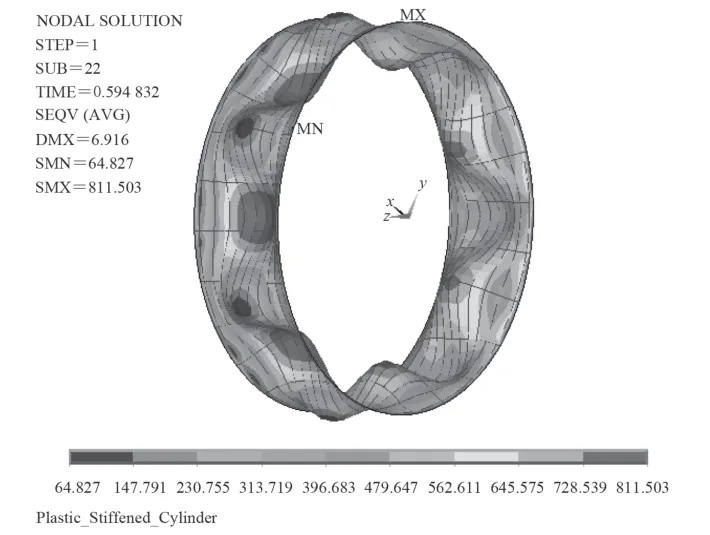
圖8 初撓度幅值為2.0 mm 的非線性計算結果Fig. 8 Nonlinear calculation results under initial imperfections amplitude 2.0 mm

表1 不同初撓度下非線性計算所得臨界載荷Tab. 1 Critical loads obtained by nonlinear calculation under different initial imperfections

4 結 語

1）Risk 法計算耐壓殼的非線性屈曲收斂性好，計算結果與實驗值較接近，具有一定的工程價值和指導意義；

2）將耐壓殼的1 階屈曲模態作為初始缺陷波型引入是合理的；

3）外形有初始缺陷的耐壓殼臨界載荷遠小于外形完美的耐壓殼，初始缺陷撓度幅值越大，耐壓殼的承載能力越差，為了保證耐壓殼的安全可靠，必須嚴格控制加工工藝誤差；

4）本文采用的材料應力應變曲線是理想化的，與真實曲線存在差異，這種差異對非線性分析結果有影響。為了使計算更加準確，有必要通過材料力學實驗得到準確的應力應變曲線。