基于p-y 曲線法對可伸縮樁側向承載力的研究

紀傳鵬，徐勝文，汪學鋒，丁愛兵，劉曉雷

(1. 上海交通大學 海洋工程國家重點實驗室，上海 200240；2. 高新船舶與深海開發裝備協同創新中心（船海協創中心），上海 200240；3. 上海交通大學 船舶海洋與建筑工程學院，上海 200240)

0 引 言

淺水域的海洋結構物通常采用的定位裝置有：固定式裝置、錨泊裝置和動力定位系統。固定式海洋平臺定位精度高，但不便于平臺的轉移，當遭遇極端海況時亦無法撤離平臺易使平臺遭受損壞釀成災難。當平臺在一個位置工作時間不是很久時不適用固定式裝置，且其拆卸工作較為復雜。錨泊裝置定位精度相對較低，對于如作為海上浮式機場或鉆井平臺的海洋結構物易引起事故，且下錨和起錨過程較為復雜，需要工程輔助船的協助，耗費大量時間和成本。動力定位系統在平臺的整個工作期間均需啟動動力定位裝置，油耗高，既導致高昂成本也造成較嚴重的環境污染。

本文針對目前使用的定位裝置的不足，提出了一種新型定位裝置。該定位裝置采用可伸縮樁進行定位，以半潛式平臺為例，可伸縮樁安裝于平臺中，且相應地配套有用于升降可伸縮樁的裝置。當平臺到達工作地點時，可伸縮樁向下移動使樁低于平臺甲板，以便平臺在工作狀況下可充分利用其平臺區域。然后樁開始伸出直至觸碰到海床，接著使可伸縮樁長度固定且平臺注入壓載水把樁壓入海床一定距離。之后保持樁與土壤不脫離，邊伸長可伸縮樁邊排出平臺壓載水減小平臺吃水，以增大樁頂部的垂向力加快進樁過程。重復這一過程直至樁達到設計插深，如圖1所示。當平臺完成工作任務或遇到極端海況需要轉移時，排出平臺內壓載水使樁與土壤脫離，然后使樁收縮并存放回平臺中。插樁和拔樁過程均可由浮體自身完成而無須工程輔助船協助，方便迅速，費用較低。定位裝置定位精度高，機動性能好，適用于海上浮式機場或島礁綜合補給基地等。特別是對于作用海上浮式機場的超大型浮體[1-6]，應用可伸縮樁定位裝置后，浮體對于飛機起降所帶來劇烈變化的載荷定位裝置的運動響應較小，且工作狀態下樁移至浮體甲板以下，不會干擾甲板作為飛機跑道。應用于生活平臺上可提高平臺上人員的舒適感。

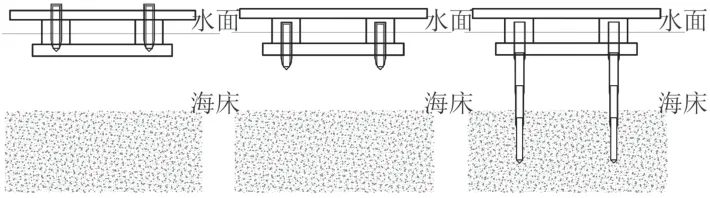
圖1 新型定位裝置插樁過程示意圖Fig. 1 Plugging process of the novel positioning facility

三維有限元分析可以較準確地模擬樁與土壤的相互作用，但為了保證計算精度，樁土接觸面處的網格應足夠細進而導致整個模型的網格數量很大，如本文中的三維有限元模型網格數量為幾萬，單次靜力分析時間為幾小時至幾十小時，這對計算時間和計算機的內存要求很高。如果在后續同時研究整個平臺所有樁的響應仍采用三維有限元法將需要更多的計算資源，為了減小計算資源，可采用p-y 曲線法模擬土壤對樁的作用，該理論是用一系列沿深度方向分布，剛度與樁在相對應深度處p-y 曲線吻合的非線性彈簧模擬土壤對樁的支承作用，如圖2 所示。采用該方法和三維有限元分析法計算樁在相同側向載荷下得到樁的位移響應基本相同，進而可用于在后續研究中簡化模擬土壤支承作用以提高計算效率。

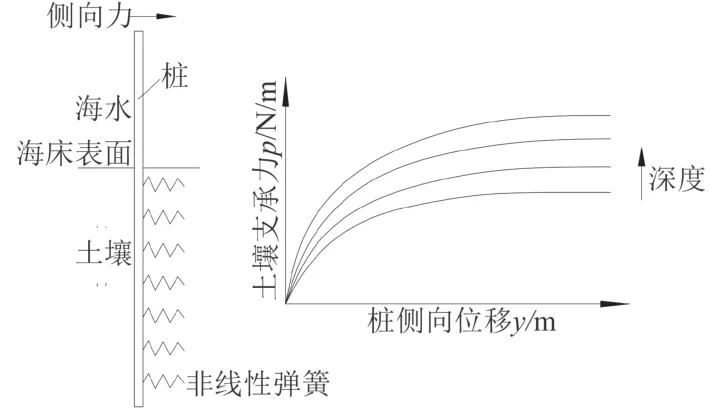
圖2 p-y 曲線法模擬側向承載樁原理圖Fig. 2 Diagram of the lateral loaded pile simulated by p-y curve method

自從McClelland 和 Focht[7]提出p-y 曲線法模擬樁-土相互作用，p-y 曲線法已被廣泛運用于側向承載樁的評估中。p-y 曲線法已被美國石油學會（API）[8]和挪威勞氏船級社（DNV GL）[9]的海洋結構物設計規范所采納，按照規范中的要求，樁的p-y 曲線應通過樁的模型試驗或半經驗公式獲得。但規范中提供的計算py 曲線的經驗公式是基于小樁徑（小于3 m）均勻樁得到的，對本文的大樁徑可伸縮樁不適用。文獻[10 - 16]對側向承載均勻樁在靜態和動態側向載荷下的響應進行了研究，并與模型試驗結果比較驗證了有限元法在計算樁的承載力上的適用性和準確性。但目前尚無針對可伸縮樁側向承載力的研究，本文通過三維有限元法計算可伸縮樁的p-y 曲線并分析其側向承載能力。

1 p-y 曲線法與三維有限元法比較

本文以一個工作海域水深為50 m 的超大型浮體為例，可伸縮樁定位裝置布置于浮體中。在Abaqus 中建立3 m 樁徑均勻樁和海床的三維有限元模型如圖3 所示，樁的插深為50 m。為模擬載荷為水面處平臺傳遞到樁上，樁比海床表面高出50 m，且在海床上方50 m 處建立參考點RP-1，與樁的上端建立剛體約束，模擬樁與平臺間的剛性連接。平臺傳遞到樁上的載荷通過加載在RP-1 上傳遞給樁模型。

圖3 樁和土壤的三維有限元模型Fig. 3 The 3D FE model of the pile and the soil

樁模型采用彈性本構模型，由S4R 單元組成，采用鋼的材料屬性，彈性模量為206GPa，泊松比為0.3，質量為7 840kg/m3。為減小邊界效應的影響，土壤模型直徑為20 倍樁徑，高度為樁插深加10 倍樁徑。土壤模型采用摩爾庫倫本構模型，干重度為8.1 kN/m3，黏聚力為31.9 kPa，摩擦角為11.6°，彈性模量為5 MPa，泊松比為0.35。考慮到該加載過程是在不排水條件下完成的，設置土壤中的滲透率為1×10-6m/s，初始孔隙比為1.0，土壤孔隙流體重度為10 046 N/m3。土壤模型由C3D10 單元組成，該類型單元只有平移自由度沒有轉動自由度。邊界條件設置為土壤底部限制所有平移自由度，土壤側面限制水平方向平移自由度。樁與土壤的接觸面設置為“罰”接觸，法線方向為硬接觸，切線方向摩擦系數設置為0.25。

在三維樁-土有限元模型的參考點RP-1 中施加水平側向載荷進行靜力分析，并從計算結果中提取出樁在不同深度位置處的p-y 曲線，用梁和一系列非線性彈簧模擬樁和土壤支承力，將提取到的p-y 曲線數據作為相應彈簧的剛度，比較在相同側向載荷下三維模型樁和梁模型樁的側向位移如圖4 和表1 所示。

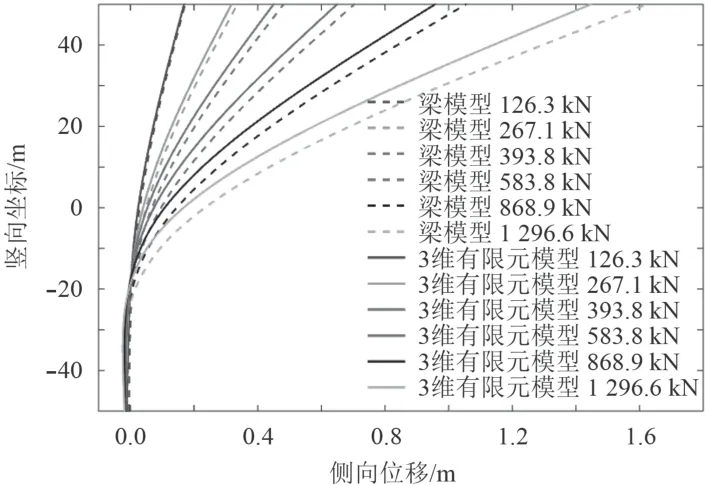
圖4 三維模型樁和梁模型樁側向位移比較Fig. 4 Comparison of the lateral displacement in the 3D pile model and the beam model

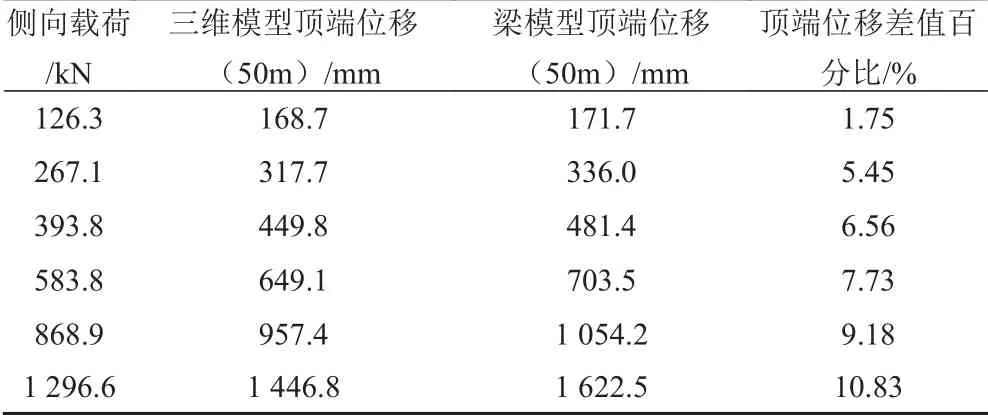
表1 三維模型樁與梁模型樁側向位移特征值比較Tab. 1 Comparison of the lateral displacement in the 3D pile model and the beam model

圖3 中縱坐標0 代表海床表面，-50 m 代表樁尖位置，50 m 代表水面位置。三維模型中樁與梁模型中樁的在相同側向載荷下的側向位移符合較好，樁頂端位移差值最大不超過11%，證明p-y 曲線法具有較高的準確性，可用于下文分析不同深度處的土壤側向支承力。

2 可伸縮樁與均勻樁的側向承載力比較

3-4-5-6 m 可伸縮樁實際插入土壤中只有處于下方的2 節，即樁徑分別為3 m 和4 m 的2 節，土壤對樁的支承力也是通過作用在這2 節上實現的。本節主要研究3-4-5-6 m 可伸縮樁與3 m 樁徑均勻樁和4 m 樁徑均勻樁的側向承載能力對比，分析可伸縮樁結構在側向承載力方面的表現狀況。建立插深均為50 m 的3 m樁徑均勻樁、4 m 樁徑均勻樁和3-4-5-6 m 可伸縮樁的三維有限元模型(見圖5)，通過加載側向載荷比較其側向位移響應和各深度處的p-y 曲線。

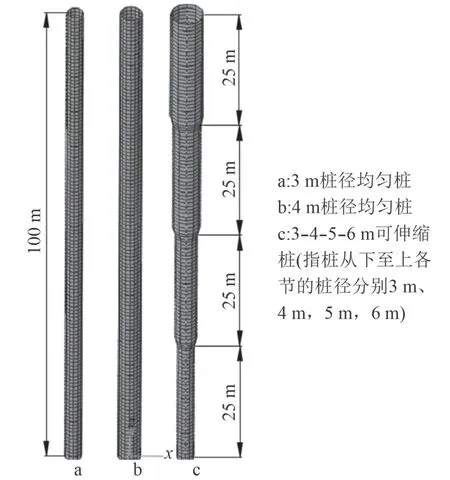
圖5 3 m，4 m 均勻樁和3-4-5-6 m 可伸縮樁的三維有限元模型Fig. 5 3D FE models of the 3m and 4m uniform piles and the 3-4-5-6m telescopic pile

從圖6 可以看到，在側向載荷較大（2 000 kN和4 000 kN）的2 組工況中，3-4-5-6 m 可伸縮樁的側向位移與4 m 樁徑均勻樁的側向位移非常相似；在側向載荷較大（6 000 kN 和8 000 kN）的2 組工況中，3-4-5-6 m 可伸縮樁的側向位移比4 m 樁徑均勻樁的側向位移略大。在所有4 組工況中3-4-5-6 m 可伸縮樁的側向位移均明顯小于3 m 樁徑均勻樁，所以3-4-5-6 m可伸縮樁的側向承載能力與4 m 樁徑均勻樁接近，明顯優于3 m 樁徑均勻樁。插入土壤部分的樁中，上半部分樁的側向位移較大，而處于側向位移拐點之下的樁側向位移很小，拐點至海床表面這段樁所受到的土壤支承力對整個樁的側向承載能力貢獻較大，而拐點之下的部分樁對整個樁的側向承載能力相對較小。所以3-4-5-6 m 可伸縮樁的側向承載能力更接近于4 m 樁徑均勻樁。樁所承受的側向載荷越大，拐點位置越靠下，當側向載荷大于6 000 kN 時，拐點位于可伸縮樁最下方一節的位置，即此時最下方一節部分參與到對側向承載能力貢獻較大的那一段，而其樁徑（3 m）比其上方一節樁徑（4 m）小，該部分的側向承載能力也會比較小。所以當側向載荷大于6 000 kN（此時對應拐點位于可伸縮樁最下方2 節的過渡處）時，側向載荷越大，3-4-5-6 m 可伸縮樁的側向支承能力比4 m 樁徑均勻樁小越多。

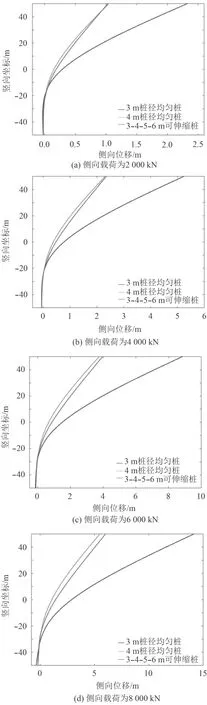
圖6 3 m，4 m 均勻樁和3-4-5-6 m 可伸縮樁的側向位移比較Fig. 6 Comparison of the lateral displacements of the 3 m and 4m uniform piles and the 3-4-5-6 m telescopic pile

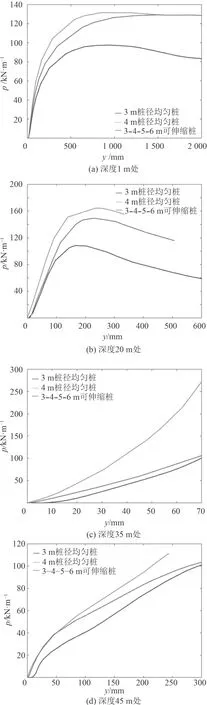
圖7 3 m，4 m 均勻樁和3-4-5-6 m 可伸縮樁在不同深度處的p-y 曲線比較Fig. 7 Comparison of p-y curves in various depths of the 3 m and 4m uniform piles and the 3-4-5-6 m telescopic pile

從圖7 可以看出，在插入土壤可伸縮樁的上方一節深度范圍內（深度0～25 m），3-4-5-6 m 可伸縮樁的p-y 曲線形狀接近于4 m 樁徑均勻樁，即在該范圍內的側向承載力與4 m 樁徑均勻樁相似。而在下方一節深度范圍內（深度25～50 m），3-4-5-6 m 可伸縮樁的p-y 曲線形狀接近于3 m 樁徑均勻樁，即該范圍內的側向承載力與3 m 樁徑均勻樁相似。這也為上文關于可伸縮樁側向承載能力分析的猜測提供了佐證。

3 可伸縮樁的動態響應

為分析可伸縮樁在實際工作當中受到往復變化波浪載荷下的運動響應，在有限元分析中加載波浪時歷載荷。本文中可伸縮樁以安裝于50 m 水域超大型浮體為例，如圖8 和表2 所示，相應的波浪載荷通過縮尺比為1∶ 100 的模型實驗測量獲得，模型實驗在上海交通大學國家海洋工程重點實驗室進行。由于樁的定位精度高，采用樁定位的平臺在波浪中的運動響應較小，實驗中將平臺設置為固定狀態，分別試驗超大型浮體在工作海況和生存海況所受到的波浪載荷。通過平臺工作海域的觀測統計，工作海況和生存海況中的波浪分別用有義波高3 m、譜峰周期7.48 s 和有義波高5 m、譜峰周期9.66 s 的Jonswap 譜模擬。在工作海況和生存海況下，由浮體平均傳遞到每個可伸縮樁腿上的水平波浪載荷如圖9 和圖10 所示。

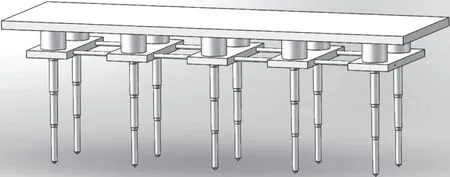
圖8 安裝可伸縮樁腿的超大型浮體示意圖Fig. 8 Very large floating structure (VLFS) installed withtelescopic piles

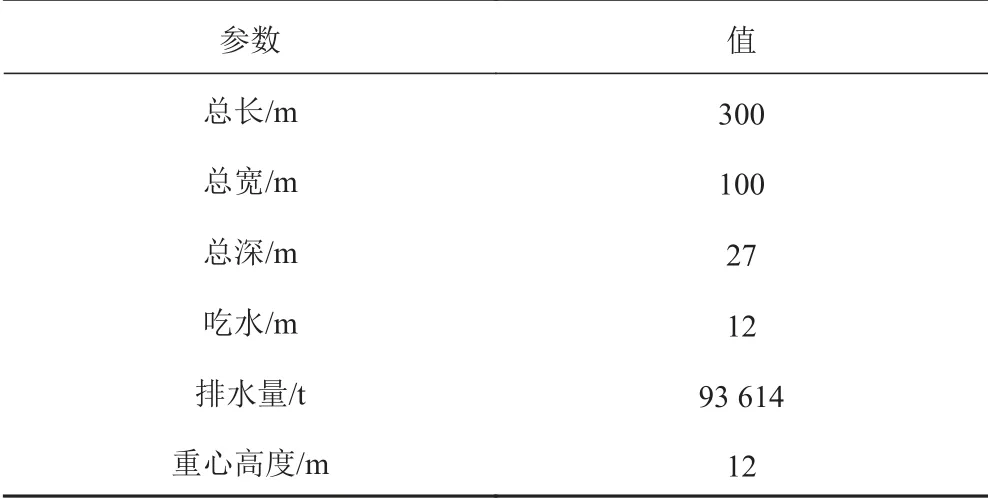
表2 超大型浮體的主要參數Tab. 2 Basic parameters of the VLFS

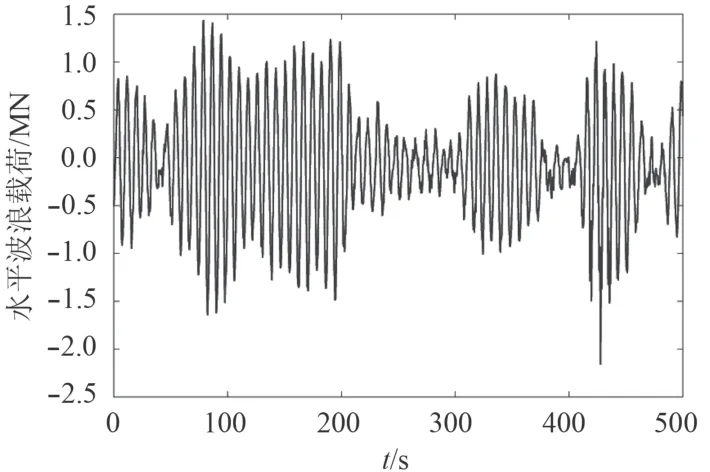
圖9 工作海況水平波浪載荷時歷曲線Fig. 9 Horizontal wave load in the operational condition

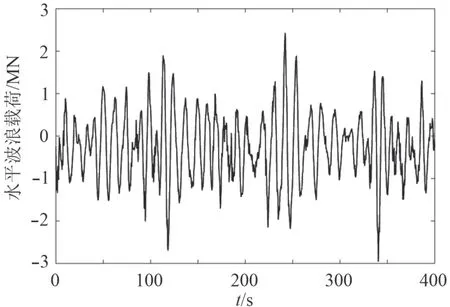
圖10 生存海況水平波浪載荷時歷曲線Fig. 10 Horizontal wave load in the survival condition

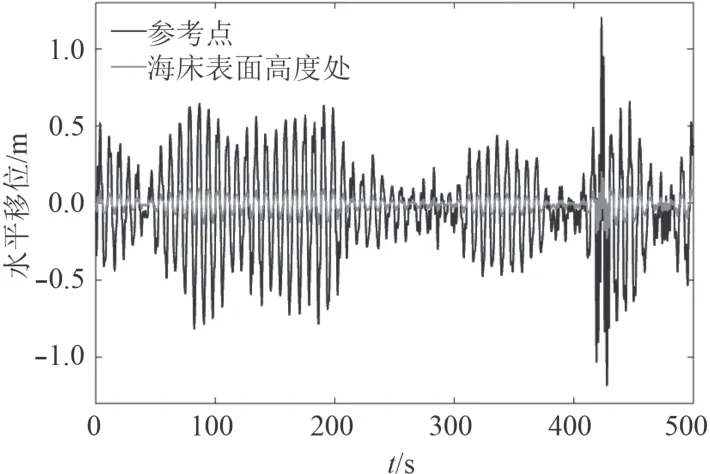
圖11 工作海況下樁的水平運動時歷響應Fig. 11 Horizontal motion response of the pile in the operational condition

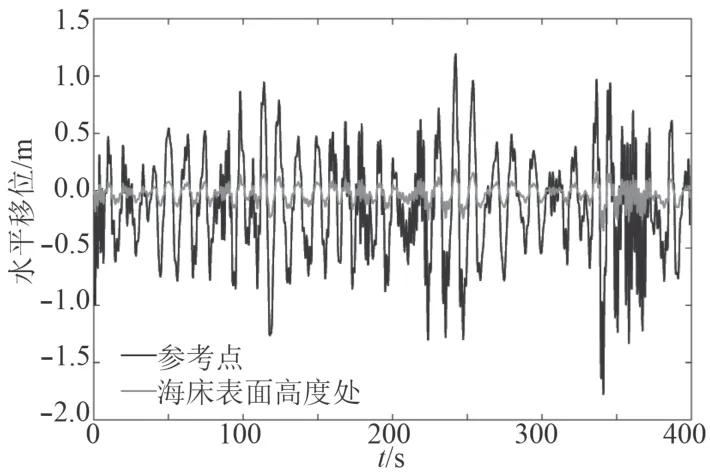
圖12 生存海況下樁的水平運動時歷響應Fig. 12 Horizontal motion response of the pile in the survival condition

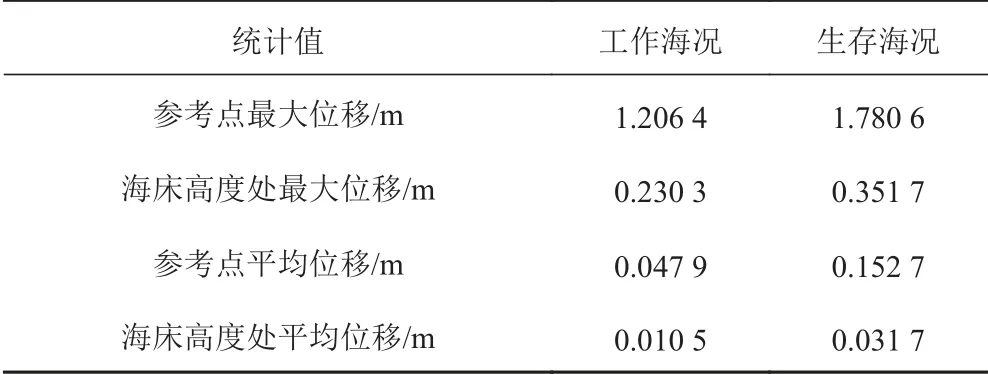
表3 樁動態位移響應統計值Tab. 3 Statics of the pile motion response

通過Abaqus/Standard 的Implicit dynamic 分析，計算樁在工作海況和生存海況的波浪載荷作用下的運動響應。分別提取工作海況和生存海況下，位于水面高度與樁連接的參考點RP-1 和樁在海床表面高度處節點的水平時歷響應，如圖11 和圖12 所示，位移響應統計值如表3 所示。從圖中可以看出樁在水平位移處的位移響應比參考點的位移響應小得多，大約是其1/5。即在波浪載荷作用下，插在土壤中樁的位移響應較小，但樁高于海床表面的長度較長（50 m），由于插于土壤中的樁發生轉動和處于海水的部分樁發生彎曲導致參考點的水平位移遠大于樁在海床表面位置處的水平響應。參考點代表了平臺與樁的連接處，所以參考點的位移響應與平臺的位移響應相似。工作海況下，樁在海床表面位置處的最大水平位移僅為0.23 m，不致引起土壤過大變形致使樁承載力下降，參考點的最大水平位移為1.2 m，定位精度遠小于傳統的錨泊定位裝置，可滿足對定位精度要求較高平臺的設計要求。生存海況下，樁在海床表面位置處的最大水平位移為0.35 m，參考點的最大水平位移為1.78 m，由于生存海況下平臺會停止工作，只需保證平臺的安全，該運動響應一般也符合設計要求。

4 結 語

本文提出了一種適用于淺水域平臺的新型定位裝置，采用可伸縮樁進行定位。基于有限元法，通過商業軟件Abaqus 對可伸縮樁的側向承載力進行分析。以3 m 樁徑均勻樁為例，比較了p-y 曲線法和三維有限元法對樁側向承載力的分析結果，驗證了p-y 曲線法的精確性。在此基礎上用p-y 曲線比較分析了3 m，4 m樁徑均勻樁和3-4-5-6 m 可伸縮樁在不同深度處的土壤支承力大小。通過比較相同側向載荷下3 種樁的側向位移曲線，發現樁位移曲線拐點以上部分樁型對樁的側向承載能力的影響比拐點以下部分樁型更大，3-4-5-6 m可伸縮樁的側向承載能力接近于4 m 樁徑均勻樁。以可伸縮樁裝置布置于超大型浮體為例，通過模型試驗獲得工作海況和生存海況下樁所承載的波浪時歷載荷，計算得到樁的動態響應。結果顯示可伸縮樁的動態響應較小符合工作和安全要求。可伸縮樁具有較好的側向承載能力，該定位裝置值得進一步研究以考慮應用到實際工程中。