約束阻尼層對復(fù)合材料層合板聲輻射的影響
楊智雄,石 敏,黃惜春,任春雨
(1. 華中科技大學 船舶與海洋工程學院,湖北 武漢 430074;2. 海軍研究院,北京 100161;3. 中國艦船研究設(shè)計中心,湖北 武漢 430064)
0 引 言
板殼結(jié)構(gòu)的減重及聲隱身性問題一直是軍事領(lǐng)域的重要研究課題。與傳統(tǒng)金屬板相比,復(fù)合材料層合板結(jié)構(gòu)以其比剛度大、比強度高等特性愈益廣泛應(yīng)用于艦船、潛艇等結(jié)構(gòu)中,軍事意義重大。復(fù)合材料帶來減重優(yōu)勢的同時,其振動致聲問題逐漸引起重視。對于這類問題,目前最普遍的做法是在結(jié)構(gòu)表面敷設(shè)約束阻尼層來顯著提高結(jié)構(gòu)阻尼,增大剪切變形,從而達到減振降噪的目的[1-2]。但是目前關(guān)于復(fù)合材料約束阻尼板的研究主要局限在固有頻率和模態(tài)阻尼等問題方面[3-7],而關(guān)于各參數(shù)對層合阻尼板聲輻射的影響研究還遠不如傳統(tǒng)三明治結(jié)構(gòu)那樣充分[8-11]。面板厚度、芯層厚度和位置以及不同鋪層角導(dǎo)致纖維長度的改變均可能對該結(jié)構(gòu)聲輻射產(chǎn)生影響。了解層合阻尼板的振聲特性規(guī)律有助于充分利用阻尼材料,達到更高效地降低結(jié)構(gòu)噪聲的目的。
另一方面,有限元法在求解復(fù)雜幾何和邊界條件問題上的顯著優(yōu)勢,愈益受到研究者們的青睞。由于各向異性復(fù)合材料以及粘彈性芯層材料的存在,結(jié)構(gòu)剪切效應(yīng)非常明顯。因此如何基于有限元法準確高效的對該結(jié)構(gòu)進行動力學分析是個難題[12-13]。針對這種結(jié)構(gòu),常用有限元離散方式有3 種:1)基于一階剪切變形理論(FSDT)或高階剪切變形理論(HSDT)的殼單元;2)基于分層理論(Layerwise)的連續(xù)殼單元;3)基于三維彈性理論(3-D)的體單元。以上任意一種方式均不能兼顧準確性與計算量問題。而同時采用8 節(jié)點三位移自由度的連續(xù)殼單元與8 節(jié)點三位移自由度的體單元的有限元離散方式,既可以充分考慮結(jié)構(gòu)的剪切變形,又可以降低計算量,2 種單元之間還有很好的位移協(xié)調(diào)性。
本文在Li[14]基礎(chǔ)上引入約束粘彈性阻尼層,采用連續(xù)殼單元離散約束面板和基板,而用體單元離散阻尼層,建立有限元模型,并結(jié)合聲學無限元技術(shù),通過算例驗證了該方法振聲分析的準確性。同時開展了面板厚度、芯層厚度和位置以及鋪層角對結(jié)構(gòu)振聲特性影響規(guī)律的研究,從而為復(fù)層合阻尼板的低噪聲設(shè)計提供依據(jù)。
1 分層模型
鑲嵌在無限大剛性障板中的復(fù)合材料約束阻尼層合板結(jié)構(gòu)如圖1 所示。板上表面位于平面 z=0上。z ≥0 半空間內(nèi)充滿密度為 ρ的空氣流體,板在一簡諧激振力作用下向半空間內(nèi)輻射聲功率。 z <0半空間為真空狀態(tài),假設(shè)不考慮空氣與結(jié)構(gòu)的相互耦合作用。基板與面板厚度分別為tb,tf,采用8 節(jié)點連續(xù)殼單元進行離散,阻尼層厚度為tv,采用8 節(jié)點的體單元離散。
以復(fù)合材料層合板為例,考慮建立基于線性分層理論的有限元模型,其位移模型如圖2 所示。假設(shè)層合板厚度方向分為 Ne(N=Ne+1)個子層,則結(jié)構(gòu)上任意位置 (x,y,z)處的位移分量可表示為:
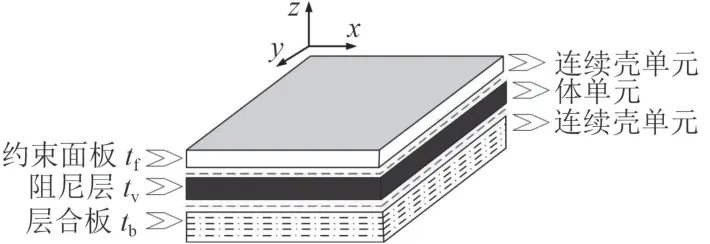
圖1 復(fù)合材料約束阻尼板結(jié)構(gòu)示意圖Fig. 1 The figuer of a composite constrained damping plate
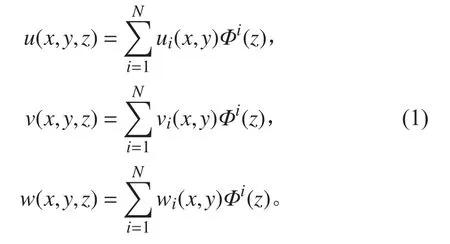
其中: (ui,vi,wi) 為第i個交界面上任意點的位移;Φi(z)為厚度坐標的線性連續(xù)分段函數(shù):
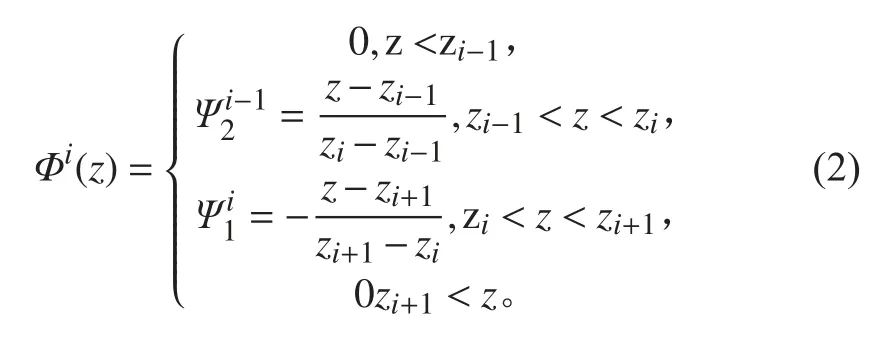
為了建立基于線性分層理論的有限元模型,第i 層上任意一點處位移,ui(x,y),vi(x,y)和wi(x,y)可通過二維線性拉格朗日插值多項式進行擬合:
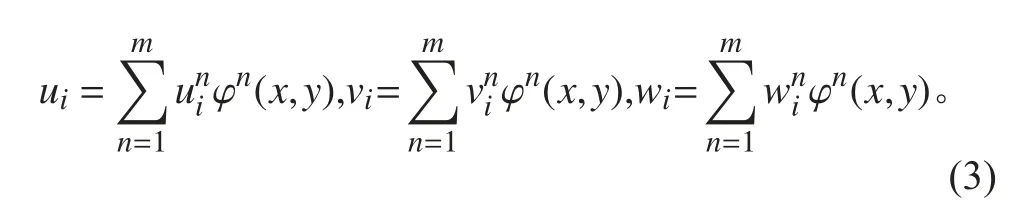
其中:m 為每個單元的節(jié)點數(shù)目; φ(x,y)為二維拉格朗日積分函數(shù);為第i 個數(shù)值層上二維有限板單元上第n 個節(jié)點的3 個位移分量。
利用上述任意子層位移表達式并結(jié)合正交材料應(yīng)力應(yīng)變關(guān)系以及轉(zhuǎn)應(yīng)力軸公式,可得到層合板的單元剛度矩陣以及單元質(zhì)量矩陣。同樣可得到面板相應(yīng)的單元剛度及質(zhì)量矩陣。
為了精確描述低模量阻尼層的剪切變形,引入八節(jié)點三位移自由度的體單元來離散粘彈性芯層,具體可參考文獻[3]。同時,體單元與連續(xù)殼單元3 個位移自由度完全一樣,因此基板、芯層與面板三者之間具有有很好的位移協(xié)調(diào)性。芯層彈性模量采用復(fù)數(shù)形式表示 E=Ev(1+iη),其中η 為材料損耗因子。
利用不同類型單元離散得到的面板、芯層以及層合板的單元、質(zhì)量剛度矩陣進行裝配可得到結(jié)構(gòu)整體的剛度矩陣K 以及質(zhì)量矩陣M。代入到歐拉拉格朗日運動方程以及虛功方程里并經(jīng)過一系列積分簡化,可得到在簡諧力作用下在特定頻率下的結(jié)構(gòu)運動方程:
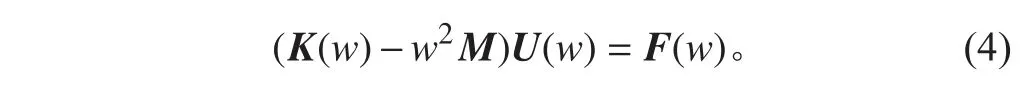
其中: M , K(w) 以及 F(w)分別為結(jié)構(gòu)的總體質(zhì)量矩陣,剛度矩陣以及載荷矢量; U為節(jié)點的位移矢量。
2 聲學方程
聲音在理想空氣介質(zhì)中傳播時,若不考慮時域特性,則流場中聲壓要滿足Helmholtz 方程:
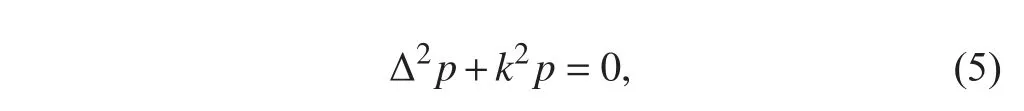
式中: k 表示波數(shù); Δ2表示拉普拉斯算子。
聲波在有限流場中傳播時,由于邊界阻抗的存在必然存在聲波的反射,采用聲學無限元技術(shù),可在有限流體邊界上覆蓋一層無限單元來實現(xiàn)對無限流場的模擬。此時,聲波就能夠滿足在流場無窮遠邊界條件上的Sommerfield 輻射條件:
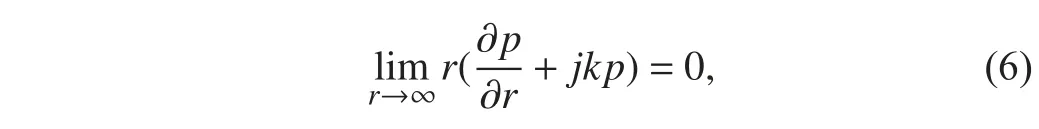
若已知聲輻射表面的速度分布,則聲壓速度關(guān)系滿足的邊界條件:
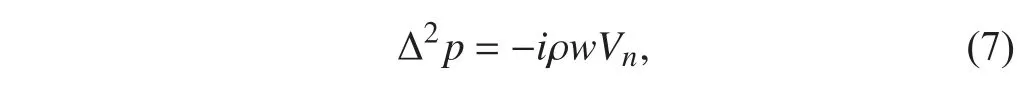
對Helmholtz 方程應(yīng)用Galerkin 加權(quán)殘值法,并分別對流體區(qū)域 V 、有限流場內(nèi)邊界 Γi、外邊界 Γe積分可得
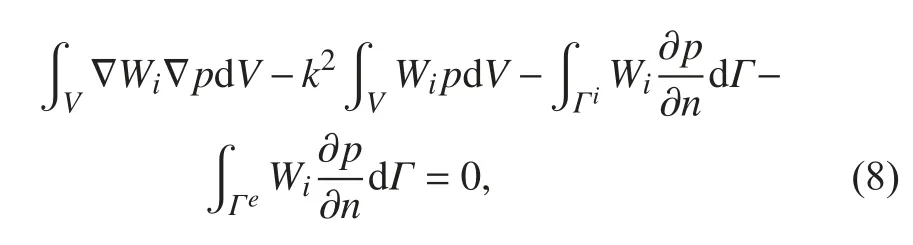
其中:p 為聲壓值函數(shù);Wi為加權(quán)函數(shù)。
結(jié)合上式以邊界條件,隨著r→∞,有p→∞以及Γe→∞,通過線性插值函數(shù),可得到
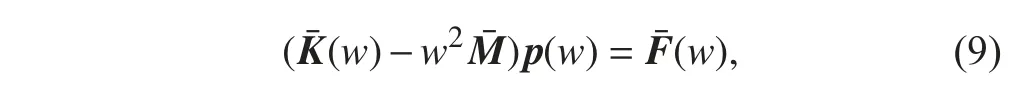
求得結(jié)構(gòu)表面S 上的聲壓和法向速度后,結(jié)構(gòu)的輻射聲功率可通過下式求得:
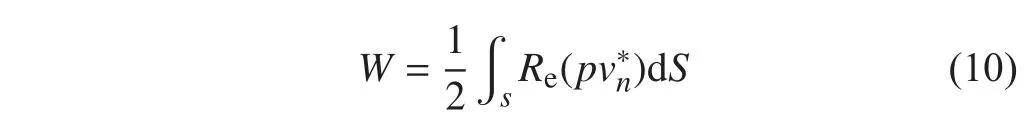
式中:p 和vn分別為結(jié)構(gòu)表面聲壓和表面法向振速;表示vn的共軛復(fù)數(shù);Re()表示取實數(shù)。取空氣中速度參考值為5×10-8m/s,輻射聲功率參考值為1×10-6W。
3 數(shù)值分析
以四邊固支的復(fù)合材料約束阻尼板為例,其基板、粘彈性阻尼層及面板的材料屬性如表1 所示。其中,基板為各向異性層合板,厚度tb=5 mm,包含5 個厚度均為1 mm 的單層板,初始鋪設(shè)角度為[0/90/0/90/0]。阻尼層及面板為各向同性材料,初始厚度tv,tf均為0.5 mm。結(jié)構(gòu)長寬尺寸為600 mm×400 mm。單位簡諧激勵力位于(0.1 m,0.1 m,0 m)位置處,其頻率范圍為50 Hz~1kHz。空氣密度為1.21 kg/m3,空氣中聲速為343 m/s。基于LW 理論的8 節(jié)點連續(xù)殼單元離散基板及面板,基于三維彈性理論的8 節(jié)點體單元離散阻尼層,建立面內(nèi)及厚度方向上單元個數(shù)分別為60×40×7 的混合有限元模型,應(yīng)用聲學無限元方法探究阻尼層厚度、面板厚度、阻尼層敷設(shè)位置以及與阻尼層直接接觸的單層板纖維鋪設(shè)方向?qū)Y(jié)構(gòu)振聲響應(yīng)的影響。
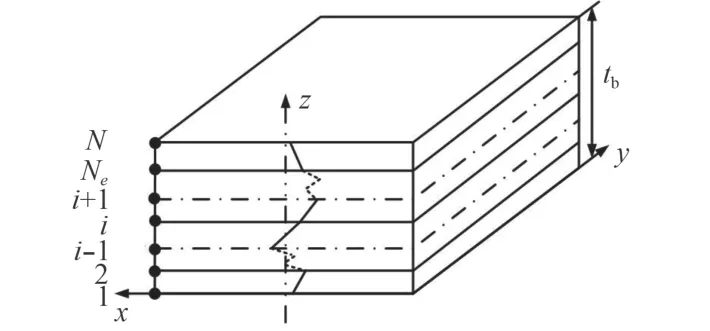
圖2 層合板線性位移模型Fig. 2 Linear layerwise model of a laminated plate
3.1 算例分析
分別計算Li[14]中復(fù)合材料層合板以及Assaf[8]中三明治板的振聲頻響,并與文獻結(jié)果進行對比,驗算本文分析模型的準確性。其中,四邊固支復(fù)合材料層合板材料屬性、幾何尺寸同上述基板一致,采用連續(xù)殼單元進行離散;簡支三明治板長寬分別為0.48 m,0.42 m,各向同性上下面板厚度分別為3 mm,0.5 mm,采用連續(xù)殼單元進行離散;粘彈性芯層厚度為0.25 mm,用體單元進行離散。面板及芯層材料屬性如表1 所示。2 種結(jié)構(gòu)的表面均方振速計算結(jié)果如圖3 所示,輻射聲功率結(jié)果如圖4 所示。
從圖3 和圖4 可知,本文建立的有限元模型計算結(jié)果分別與文獻[8,14]中的結(jié)果一致,驗證了該方法的準確性。基于此方法建立上述層合阻尼板的有限元混合模型并進行振聲計算。由圖3 和圖4 可知,與無阻尼的層合板相比,敷設(shè)約束粘彈性阻尼層的復(fù)合材料層合板的表面均方振速以及輻射聲功率均大幅降低。如在0~800 Hz 范圍內(nèi)無阻尼板的平均均方振速以及輻射聲功率分別為85.43 dB,71.17 dB,而層合阻尼板的平均均方振速以及輻射聲功率分別為82.04dB,65.65 dB 頻率,二者分別相差3.39 dB,6.52 dB。由此可見,粘彈性材料對復(fù)合材料層合板結(jié)構(gòu)有顯著的減振降噪效果。

表1 復(fù)合材料約束阻尼板材料屬性Tab. 1 Material properties of the composite constrained damping plate
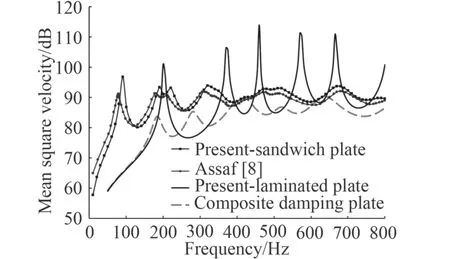
圖3 均方振速校驗Fig. 3 Validation of the mean square velocity
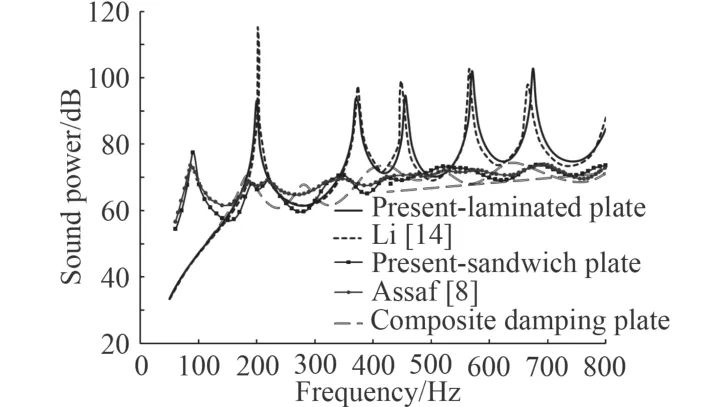
圖4 輻射聲功率校驗Fig. 4 validation of the sound power
3.2 面板厚度影響
考慮上述層合阻尼板,保持基板厚度tb、芯層厚度tv等其他條件不變,改變表層面板厚度tf,使得tf/tv分別為1/2,1 以及2 時分析結(jié)構(gòu)振聲頻響特性。層合阻尼板結(jié)構(gòu)在不同面板厚度下的均方振速、輻射聲功率見圖5 和圖6。
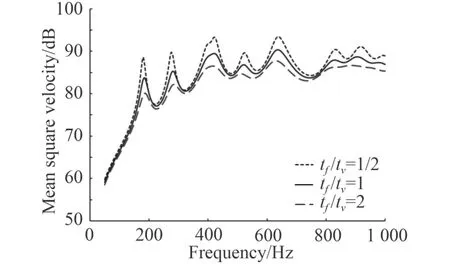
圖5 面板厚度對均方振速影響Fig. 5 Influence of panel thickness on mean square velocity
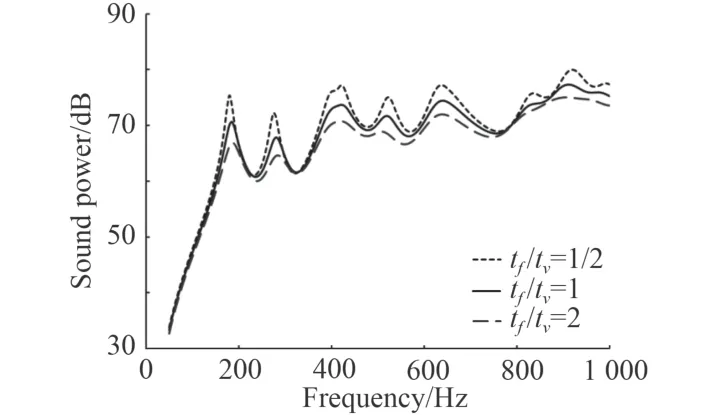
圖6 面板厚度對輻射聲功率影響Fig. 6 Influence of panel thickness on sound power
從圖5 和圖6 可知,隨著面板厚度增加,結(jié)構(gòu)表面均方振速以及輻射聲功率在整個頻段范圍內(nèi)均有明顯下降。如tf/tv分別為1 和2 時,相較于tf/tv為1/2,平均均方振速依次降低1.43 dB,2.86 dB,平均輻射聲功率依次降低1.36 dB,2.83 dB。但在不同厚度面板下,各個峰值對應(yīng)處的頻率幾乎無差別。這是由于增加的面板厚度對結(jié)構(gòu)的比剛度影響較小,因此對固有頻率影響不大,但是增大面板厚度能有效增加芯層的剪切變形,大量消耗結(jié)構(gòu)振動時的能量,從而可以降低均方振速和聲功率。
3.3 阻尼層厚度影響
由3.1 節(jié)可知,敷設(shè)粘彈性芯層材料的層合阻尼板可以顯著降低振聲水平,由此考慮阻尼層厚度將直接影響結(jié)構(gòu)的振聲響應(yīng)。在初始面板、阻尼厚度均為0.5 mm 的基礎(chǔ)上,增加兩組阻尼厚度分別為0.33 mm、1 mm 的方案,探究阻尼層厚度對結(jié)構(gòu)的均方振速及輻射聲功率影響,分別如圖7 和圖8 所示。

圖7 阻尼層厚度對均方振速影響Fig. 7 Influence of damping layer thickness on mean square velocity
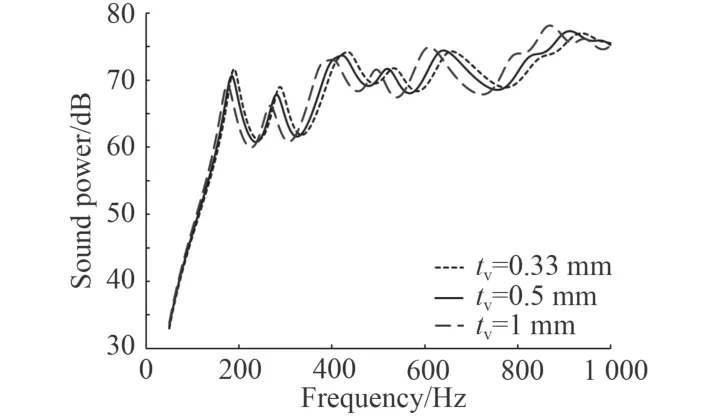
圖8 阻尼層厚度對輻射聲功率影響Fig. 8 Influence of damping layer thickness on sound power
從圖7 和圖8 的均方振速及輻射聲功率頻率曲線可知,增加阻尼層厚度對各峰值大小無明顯影響。在整個頻率范圍內(nèi),阻尼厚度分別為0.33 mm,0.5 mm,1 mm 時的頻域平均均方振速分別為82.94 dB,83.22 dB,83.68 dB,而平均輻射聲功率分別為67.5 dB,67.68 dB,67.76 dB,可見,隨著芯層厚度增加,結(jié)構(gòu)的振聲水平均有不同程度上升。另外,增加芯層厚度后,結(jié)構(gòu)固有頻率向低頻段偏移,且低階模態(tài)偏移較小,高階模態(tài)偏移越來越顯著。這是由于芯層厚度增加降低了結(jié)構(gòu)的比剛度,導(dǎo)致結(jié)構(gòu)固有頻率有所降低。由上可見,增加芯層厚度,一方面降低了結(jié)構(gòu)整體的比剛度,使得固有頻率減小,另一方面,阻尼材料剪切變形所吸收的能量減小,使得振聲水平略有上升。因此應(yīng)當合理選擇阻尼層厚度,過分追求阻尼層厚度對降低結(jié)構(gòu)的聲輻射水平無益,相反會增加結(jié)構(gòu)重量。
3.4 阻尼層位置影響
保持阻尼層厚度等其他條件不變,考慮3 種約束阻尼層敷設(shè)位置的情況:L1-層合板上表面、L2-層合板中面、L3-層合板上下表面各1/2。阻尼層位置示意圖如圖9 所示。不同敷設(shè)方式對結(jié)構(gòu)均方振速和輻射聲功率的影響規(guī)律如圖10 和圖11 所示。
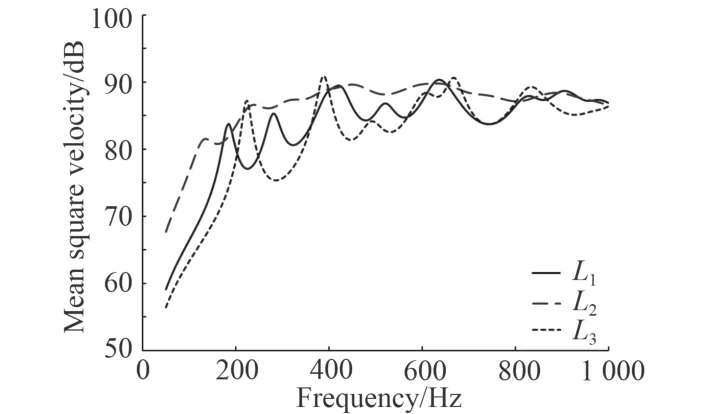
圖10 阻尼層位置對均方振速影響Fig. 10 Influence of damping layer locations on mean square velocity
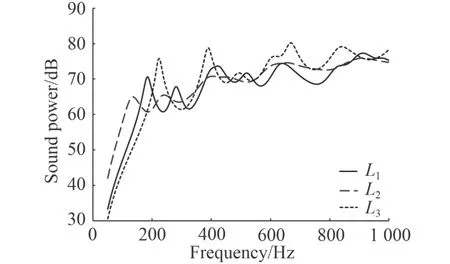
圖11 阻尼層位置對輻射聲功率影響Fig. 11 Influence of damping layer locations on sound power
從圖10 和圖11 中可以看到,3 種阻尼敷設(shè)方式對結(jié)構(gòu)的振聲規(guī)律影響較大。從平均均方振速方面來看,對于相同厚度的約束阻尼層,最優(yōu)敷設(shè)方式依次為L3,L2,L1。如L3的平均均方振速為81.58dB,顯著低于其他2 種方式的平均均方振速值83.22 dB,86.39 dB。由此可見,此時分開敷設(shè)阻尼有利于提高了結(jié)構(gòu)的整體剛度,使得振動水平降低。同時,分開敷設(shè)阻尼層方式的振動及聲輻射頻響曲線上的各共振峰頻率均高于另外2 種敷設(shè)方式,這同樣證明了該敷設(shè)方式有利于增加結(jié)構(gòu)剛度,從而增大結(jié)構(gòu)固有頻率。從平均敷設(shè)聲功率方面來看,3 種阻尼敷設(shè)方式L1,L2,L3的平均輻射聲功率分別為67.68 dB,69.08 dB,69.07 dB。因此,約束阻尼層敷設(shè)在層合板表面最有利于降低結(jié)構(gòu)的聲輻射水平,在600~1 000 Hz 范圍內(nèi)效果更為顯著。
3.5 鋪層角度影響
為考慮與阻尼層直接接觸的單層板鋪設(shè)角度對該結(jié)構(gòu)的振聲影響,將原纖維鋪設(shè)角度為0°、厚度為1 mm 的單層板等分成0.25 mm 的4 層單層板,鋪設(shè)角度為[θ/0/0/0],其中θ 為與阻尼層毗鄰的單層板鋪設(shè)角度,分別取為0°,45°,90°。不同鋪設(shè)角度下結(jié)構(gòu)的均方振速和輻射聲功率曲線分別如圖12 和圖13 所示。
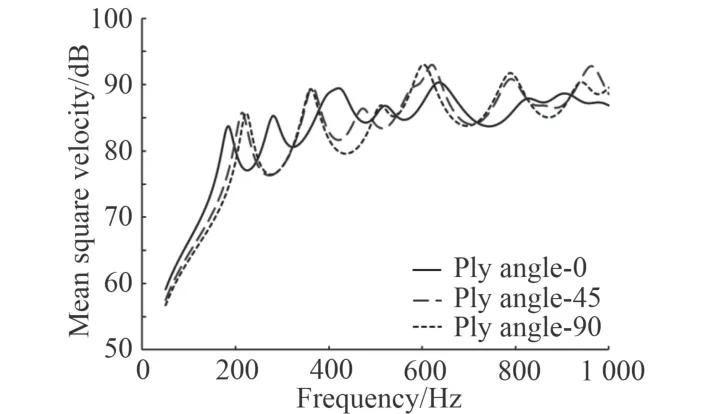
圖12 鋪設(shè)角度對均方振速影響Fig. 12 Influence of ply angle on mean square velocity
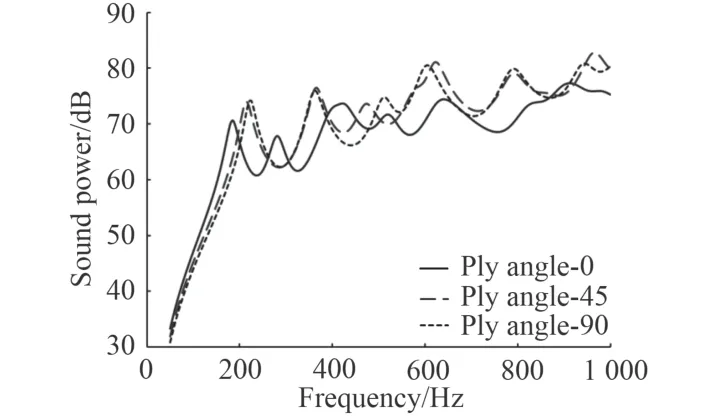
圖13 鋪設(shè)角度對輻射聲功率影響Fig. 13 Influence of ply angle on sound power
從圖12 和圖13 可知,與阻尼層直接相鄰的單層板鋪設(shè)角度對該結(jié)構(gòu)的振聲影響較大。具體來看,鋪設(shè)角度為0°時的振聲頻響曲線與角度為45°,90°時差異較大,主要表現(xiàn)為峰值對應(yīng)的固有頻率向低段偏移較為明顯,表明該鋪設(shè)角度下結(jié)構(gòu)的整體比剛度有所降低。但此時結(jié)構(gòu)的平均輻射聲功率較低,特別地,在600 Hz 以上時效果較為顯著,因此該鋪設(shè)角度有利于提高結(jié)構(gòu)的降噪能力。而鋪設(shè)角度為45°,90°時的振聲頻響規(guī)律較為相似,比較二者的平均均方振速、平均輻射聲功率,總體上鋪設(shè)角度為90°時的振聲水平要優(yōu)于鋪設(shè)角度為45°的情況。
4 結(jié) 語
1)基于連續(xù)殼單元與體單元的混合有限元模型可以有效分析層合阻尼板的振聲特性,約束粘彈性阻尼層對復(fù)合材料層合板有顯著的減振降噪效果。
2)一定限度的增大約束面板厚度能有效提高芯層的剪切變形,從而顯著降低均方振速和聲功率;相反,過分追求阻尼層厚度不利于降低結(jié)構(gòu)的振聲水平,還會犧牲一部分重量。
4)阻尼層敷設(shè)在層合板表面,相較于板中面或在上下表面分開敷設(shè)方式,更能充分利用阻尼的降噪作用,提高聲隱身的效率。
5)與阻尼層直接毗鄰的單層板鋪設(shè)角度對結(jié)構(gòu)振聲影響較大,當角度為0°時,平均輻射聲功率低于另2 種鋪設(shè)角度。

